平面波特性
良导体表面平面电磁波传播特征

良导体表面平面电磁波传播特征
良导体表面平面电磁波传播特征是指在良导体表面上传播的电磁波的
特性。
以下是其主要特征:1.波长短:由于良导体表面平面电磁波是在导
体表面上传播的,因此波长非常短,通常比自由空间中的波长短得多。
2.
衰减快:良导体表面平面电磁波在传播过程中会受到导体表面的阻抗影响,导致波的能量迅速衰减,因此传播距离较短。
3.反射强:由于良导体表面
平面电磁波在传播过程中会受到导体表面的反射,因此反射强度非常大,
可以达到100%。
4.极化方向:良导体表面平面电磁波的极化方向垂直于
导体表面,因此在传播过程中会受到导体表面的影响,导致波的极化方向
发生变化。
5.传播速度:良导体表面平面电磁波的传播速度与自由空间中
的电磁波速度相同,即光速。
总之,良导体表面平面电磁波传播特征是由
于其在导体表面上传播的特殊环境所决定的,具有波长短、衰减快、反射强、极化方向垂直、传播速度快等特点。
这些特征在电磁波传播和应用中
具有重要的意义。
平面波特性
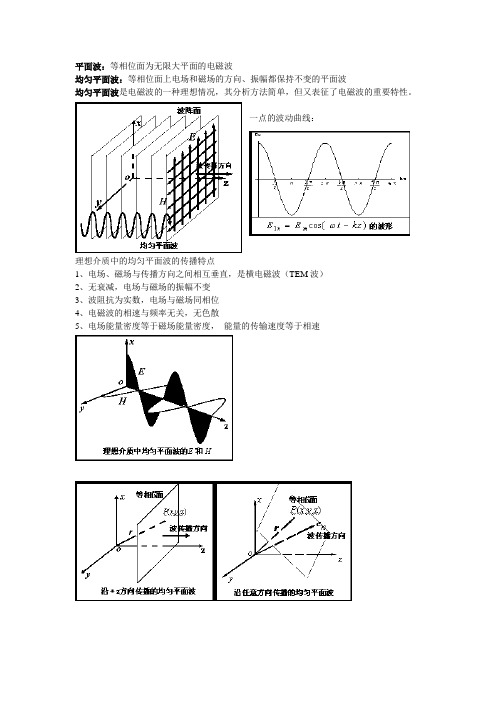
平面波:等相位面为无限大平面的电磁波
均匀平面波:等相位面上电场和磁场的方向、振幅都保持不变的平面波
均匀平面波是电磁波的一种理想情况,其分析方法简单,但又表征了电磁波的重要特性。
一点的波动曲线:
理想介质中的均匀平面波的传播特点
1、电场、磁场与传播方向之间相互垂直,是横电磁波(TEM波)
2、无衰减,电场与磁场的振幅不变
3、波阻抗为实数,电场与磁场同相位
4、电磁波的相速与频率无关,无色散
5、电场能量密度等于磁场能量密度,能量的传输速度等于相速。
均匀平面波的极化特性

6.6 均匀平面波的极化特性1.电磁波的极化定义2.电磁波的极化形式1.电磁波的极化定义电磁波的极化是指空间某点的电场强度矢量方向随时间的变化规律。
用空间某点电场强度矢量的端点随时间变化所描画出的轨迹来表示。
电磁波的极化特性在日常生活中也经常使用例如:超短波收音机U E l =⋅θElcos E l =⋅θ均匀平面波的极化特性平面波的表达式:mˆcos()xE E t kz a =-+ωϕmˆcos()yH H t kz a=-+ωϕxyz2.电磁波的极化形式(1)线极化:电场强度矢量端点随时间变化的轨迹是一条直线。
yx2.电磁波的极化形式(1)线极化:电场强度矢量端点随时间变化的轨迹是一条直线。
(2)圆极化:电场强度矢量端点随时间变化的轨迹是圆。
yEx2.电磁波的极化形式(1)线极化:电场强度矢量端点随时间变化的轨迹是一条直线。
(2)圆极化:电场强度矢量端点随时间变化的轨迹是圆。
(3)椭圆极化:电场强度矢量端点随时间变化的轨迹是椭圆。
yx(1)线极化假设空间任意一个平面波:x yE E E =+若电场表示为:m ˆcos()x x x x E E t kz a ϕ=ω-+演示1——x 方向的线极化波m ˆcos()y y y y E E t kz aϕ=ω-+演示2——y 方向的线极化波线极化条件:ϕϕϕ==y x 或x y ϕϕπ-=±两个相互垂直线极化波叠加:条件:ϕϕϕ==y x 22mmcos()x y E EEt kz ωϕ=+-+与x 轴的夹角为:E θarctan()ymxmE E θ=x yE E E =+m ˆcos()x x x x E E t kz aϕ=ω-+m ˆcos()y y y y E E t kz aϕ=ω-+其中:结论:两个相互垂直线极化波叠加,其初始相位相同时,形成新的线极化波。
两个相互垂直线极化波叠加:条件:22mmcos()x y E EEt kz ωϕ=+-+与x 轴的夹角为:E θarctan()ymxmE E θ=-x yE E E =+m ˆcos()x x x x E E t kz aϕ=ω-+m ˆcos()y y y y E E t kz aϕ=ω-+x y ϕϕπ-=±其中:结论:两个相互垂直线极化波叠加,其初始相位相同时,形成新的线极化波。
第四章-平面波

第四章 平面波本章从麦克斯韦方程及物质的本构关系出发,研究在均匀介质中平面波的传播及其主要特征。
首先讨论线性、均匀、各向同性介质中均匀平面波的传播,再推广到各向异性介质中的情况。
比平面波更复杂的电磁波也可用平面波展开,本章对此也作了讨论。
最后讨论平面波传播的传输线模型,为以后用传输线模型求解复杂的场问题打下基础。
4.1得出电场强度E 与磁场强度H 满足的波方程,4.2从波方程得到简单介质中的平面波解,4.3、4.4讨论平面波的极化特性以及平面波在有耗介质中的传播,4.5介绍色散与群速的基本概念,4.6与4.7分别研究电各向异性介质和磁各向异性介质中平面波的传播特征。
4.8讨论髙斯波束的平面波展开,4.9证明电磁波沿某一方向传播可与特定参数传输线上电压、电流波的传播等效,即电磁波传播的传输线模型。
4.1 波方程3.4已分析过,麦克斯韦方程组中两个旋度方程是独立的。
在两个旋度方程中电场强度E 与磁场强度H 耦合在一起。
从解方程角度看,先要将E 跟H “去耦”,即从两个旋度方程消去H (或E ),然后得到只关于E (或H )的方程。
本节讨论无源、简单介质中麦克斯韦方程的解,所谓无源,就是指所研究的区域内不存在产生电磁场的源J 与ρv 。
对于简单介质,ε、μ是常量。
在这种特定情况下,将物质的本构关系(3.4.1)、(3.4.2)代入麦克斯韦方程(3.2.8)~(3.2.11),得到 ∇⨯E =–j ωμH (4.1.1) ∇⨯H = j ωεE (4.1.2) ∇⋅E = 0 (4.1.3) ∇⋅H = 0 (4.1.4) 式(4.1.1)、(4.1.2)两个方程中,只有E 和H 两个独立的场量,但E 和H 耦合在一起。
为了从这两个方程得到只关于E 或H 的方程,对式(4.1.1)取旋度,并将式(4.1.2)代入,得到 ()()()E E H E μεωωεωμωμ2=-=⨯∇-=⨯∇⨯∇j j j利用恒等关系()()E E E 2∇-⋅∇∇=⨯∇⨯∇,而根据式(4.1.3),0=⋅∇E ,所以上式成为022=+∇E E μεω(4.1.5)同样对式(4.1.2)取旋度,将式(4.1.1)代入,并利用式(4.1.4)及上面的矢量运算恒等关系,得到022=+∇H H μεω(4.1.6)式(4.1.5)、(4.1.6)可合并写成 ()022=⎩⎨⎧+∇HEk(4.1.7) 式中μεω22=k(4.1.8)在自由空间或真空中,μ = μ0,ε = ε0,k 记作k 000220εμω=k(4.1.9)式(4.1.5)、(4.1.6)或(4.1.7)叫做无源简单介质中的波方程,在这个方程中E 跟H 不再耦合在一起。
第五讲 平面波

= ηHr
× erz
r A
⋅
(
r B
×
r C)
=
r B
⋅
r (C
×
r A)
=
r C
⋅(
r A
×
r B)
( ) erz
erz
⋅ ⋅
r H r E
= =
erz erz
⋅ ⋅
⎜⎛⎝ηη1Hrer×z
×
r E
⎟⎞
erz
⎠ =
η=Hrerz⋅⋅(⎜⎛⎝erezrz××erηz1)
r E =
⎟⎞ ⎠ 0
=
1
η
r E
=
yˆ 1
η
E(z,t)
3. 本征阻抗(特征阻抗)
计算式 η = ωμ = ωμ = μ k ω με ε
单位:欧姆(Ω)
η数值等于电场强度与对应磁场强度的振幅之比,并且仅决定于媒质的
电磁参数。
真空中 ④结论:
η0 =
μ0 = 120π ≈ 377 (Ω ) ε0
x
Ex = Emx cos(ω t − kz + ϕ x )
亥姆霍兹方程的解
结论
①亥姆霍兹方程的解代表正弦电磁波,进一步说,它们代表着等相位面(又
称波面)为平面的平面电磁波。如果将不同nˆ 的平面波进行叠加,还可以表
示等相位面为柱面或球面等其它形式的电磁波。
②从电场和磁场的叉积关系可以看出,电磁波的电场矢量、磁场矢量与波矢量
方向两两正交,且满足右手螺旋关系 Eˆ × Hˆ = kˆ。电场和磁场只有垂直于传播
在理想电介质中的波动方程解表示为
Ei (rv,t) = Ei m cos[ω
平面波的特性与波长的计算

平面波的特性与波长的计算波动现象是自然界中普遍存在的一种物理现象,而波长是用来描述波的特性的定量指标之一。
在物理学中,平面波是一种理想化的波模型,其特性与波长之间存在一定的关系。
本文将探讨平面波的特性以及如何计算波长。
1. 平面波的特性平面波是一种在无限远处传播、波前呈平面的波动。
与球面波和柱面波不同,平面波的波阵面是一个平面,不存在波源和波纹的聚焦或发散现象。
平面波特性的关键在于其波矢和传播方向。
平面波的波矢k定义为波矢的模长与传播方向的乘积,即k = |k| * n。
其中,|k|表示波矢的大小,n表示波的传播方向,即单位矢量。
平面波的表达式可以表示为Ae^(ik·r),其中A为振幅,k为波矢,r为位置矢量。
平面波的传播速度与波矢的大小成正比,即v = ω/|k|,其中v表示传播速度,ω表示角频率。
2. 波长的计算波长是用来描述波动的空间周期性的物理量,指在一个完整波动周期内,波动传播的距离。
对于平面波来说,波长的计算可以通过波矢的大小求倒数得到。
波矢的模长|k|与波长λ之间存在以下关系:|k| = 2π/λ。
由此可得,波长λ = 2π/|k|。
这个公式说明了波矢的大小与波长之间的倒数关系,即波矢越大,波长越短,反之亦然。
以光波为例,光是一种电磁波,其波长范围很宽,从红外到紫外都有不同波长的光。
对于可见光来说,其波长范围约为380nm到780nm之间。
3. 示例计算现在我们以一个具体的例子来计算平面波的波长。
假设我们有一个平面波,其振幅A为2,波矢k为1.5。
根据前述公式,波长λ = 2π/|k| = 2π/1.5 ≈ 4.188。
根据计算结果可知,该平面波的波长约为4.188个长度单位,可以是米、厘米、纳米等等,具体的单位需根据具体的物理系统来确定。
4. 总结平面波是一种在无限远处传播且波前呈平面的波动,其特性由波矢和传播方向决定。
波长是描述波动空间周期性的物理量,对于平面波来说,波长可以通过波矢的大小求倒数得到。
第六章-平面波详解

E exEx ey Ey
两个分量可以表示成为
Ex
E e jkz jx xm
Ey
E e jkz jy ym
第六章 平面波
合成场矢量E可以写为
E ex Exme jkz jx ey Eyme jkz jy
瞬时值表达式分别为
Ex Exm cos(t kz x ) Ey Eym cos(t kz y ) E ex Exm cos(t kz x ) ey Eym cos(t kz y )
E2
1 4
E02e2az
第六章 平面波
平均磁能密度:
wav,m
1 4
H
2
1 4
E02
2
f
e2az
1 4
E02
e2
az
1 ( )2
总的平均能量密度:
wav
wav,e
wav,m
1 4
E02e2
z
1 4
E02e2
z
1 ( )2
1 4
E E
Ex2
E
2 y
Em
合成场矢量E与x轴正方向的夹角α为
arctan
Ey Ex
arctan
sin(t cos(t
x x
) )
(t
x
)
圆极化波有左旋和右旋之分,规定如下:
将大拇指指向电磁波的传播方向,其余四指指向电
第六章 平面波
场矢量E矢端的旋转方向,若符合右手螺旋关系,则 称之为右旋圆极化波;
良导体中的的平面波

良导体中的的平面波
良导体中的平面波是一种特殊的电磁波,在导体中传播。
当电
磁波穿过导体时,它会与导体中的自由电子相互作用,导致电磁波
的衰减。
在良导体中,电磁波的传播受到导体电导率的影响,电导
率越高,电磁波的衰减越严重。
在电磁波传播中,平面波是一种特定的波动形式,它的波前是
平坦的,波峰和波谷是平行的。
在良导体中,平面波的传播受到导
体的影响,导体中的自由电子会对电磁波产生阻尼效应,使得平面
波在传播过程中衰减。
这种衰减会导致电磁波的能量逐渐转化为热能,最终被导体吸收。
良导体中的平面波还受到导体内部结构的影响,比如晶格结构、缺陷等因素都会对平面波的传播产生影响。
此外,频率、波长等也
会影响平面波在良导体中的传播特性。
总的来说,良导体中的平面波受到多种因素的影响,包括导体
的电导率、内部结构以及电磁波的频率和波长等。
这些因素共同作用,决定了平面波在良导体中的传播特性和衰减程度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面波:等相位面为无限大平面的电磁波
均匀平面波:等相位面上电场和磁场的方向、振幅都保持不变的平面波
均匀平面波是电磁波的一种理想情况,其分析方法简单,但又表征了电磁波的重要特性。
一点的波动曲线:
理想介质中的均匀平面波的传播特点
1、电场、磁场与传播方向之间相互垂直,是横电磁波(TEM波)
2、无衰减,电场与磁场的振幅不变
3、波阻抗为实数,电场与磁场同相位
4、电磁波的相速与频率无关,无色散
5、电场能量密度等于磁场能量密度,能量的传输速度等于相速。
