排列组合:小球入盒
排列组合(正式版)

排列组合——隔板法隔板法就是在n 个元素间的(n-1)个空中插入 若干个(b )个板,可以把n 个元素分成(b+1)组的方法.应用隔板法必须满足三个条件:(1) 这n 个元素必须互不相异(2) 所分成的每一组至少分得一个元素 (3) 分成的组别彼此相异.【例题解析】例1、把10个相同的小球放入3个不同的箱子,每个箱子至少一个,问有几种情况?(3629=C )例2、高二年级8个班级协商组成年级篮球队,共需10名队员,每个班级至少要出一名,有多少种不同的 组成方式?分析:将10名队员理解成10个球,排成一列,共形成9个空隙,设想有7个隔板,将排成一列的10个球隔成8段,注意:任意两块隔板不能相邻!故为3679=C 种. 附加:从5个学校选出8名学生组成代表团,每校至少有一人的选法种数是多少?分析:问题转化为将8个学生分成5组,每组至少一人,故有3547=C 种选法.例3、求方程X+Y+Z+W=23的正整数解的个数.分析:我们设想有23个无区别的球排成一列,共形成22个空,可以理解为有3块隔板,将排成一列的球隔成4段,共有1540322=C 个正整数解。
对某些不符合上述隔板法条件的一些问题可以通过一些技巧“转化”为符合条件的隔板问题.〖技巧一:添加球数用隔板法〗例4、求方程X+Y+Z+W=23的非负整数解的个数.分析:注意到x 、y 、z 、w 可以为零,故上题解法中的限定“每空至多插一块隔板”就不成立了,此时只要添加四个球,给x 、y 、z 、w 各一个球。
这样原问题就转化为求X+Y+Z+W=27的正整数解的个数了,故解的个数为2600326=C .例5、20个相同的球分给3个人,允许有人不取,但必须分完,有多少种分法?分析:问题转化为:20个相同的球分给1,2,3编号的盒子,允许有盒为空,但必须分完,有多少种分法?解析:添加3个球,给3个人每人一个,问题转化为:23个相同的球分给3个人,每人至少分一个球,且必须分完,有多少种分法?也就是23个球有22个空隙,2块隔板分成三部分,231222=C 种.评述:这个问题是典型的玻瑟——爱因斯坦(Bose-Einstein )统计模型:要将k 个相同的球放入n 个不同的盒子,每盒所放球数不限,有多少种不同放法?〖技巧二:减少球数用隔板法〗例6: 将20个相同的小球放入编号分别为1,2,3,4的四个盒子中,要求每个盒子中的球数不少于它的编号数,求放法总数.分析:先在编号1,2,3,4的四个盒子内分别放0,1,2,3个球,剩下14个无区别的球,问题等价于将14个球放入4个编号为1,2,3,4的四个盒子里,每个盒子至少有一个球的问题.剩下14个无区别的球排成一列,共形成13个空,可以理解为有3块隔板,将排成一列的球隔成4段,每段至少1个,有286313=C 种.附加:20个不加区别的小球放入编号为1号、2号、3号的三个盒子里,要求每个盒内的球数不小于盒子的编号数,问有多少种放法?解析:先取出3个球,在编号1,2,3的三个盒子内分别放0,1,2个球。
解决排列组合中分组与分配问题的一类重要模型——“小球入盒”模型

解决排列组合中分组与分配问题的一类重要模型——“小球入盒”模型凤斌;叶菊【摘要】<正>数学建模是一种数学的思考方法,是运用数学的语言和方法,通过抽象、简化,建立能近似刻画并"解决"实际问题的数学模型的一种强有力的数学手段。
排列组合问题的情景设置千变万化,"小球入盒"是一类典型的数学模型,将其用来解读排列、组合问题,可以搭起挖掘知识的内涵和外延的平台,直击目标。
【期刊名称】《青苹果:高中版》【年(卷),期】2016(000)009【总页数】3页(P42-44)【关键词】排列组合;数学模型;数学手段;分配问题;组合问题;情景设置;问题解决;思考方法;非负整数;正整数解【作者】凤斌;叶菊【作者单位】安徽省宿州二中【正文语种】中文【中图分类】G634.6数学建模是一种数学的思考方法,是运用数学的语言和方法,通过抽象、简化,建立能近似刻画并“解决”实际问题的数学模型的一种强有力的数学手段。
排列组合问题的情景设置千变万化,“小球入盒”是一类典型的数学模型,将其用来解读排列、组合问题,可以搭起挖掘知识的内涵和外延的平台,直击目标。
模型1(球少盒多)5个不同的球,放入8个不同的盒子中,每盒至多放1个球,共有多少种放法?解析(方法一)由于球与盒子均不同,每盒至多放1个球,所以这是一个排列问题,可直接从8个不同盒子中取出5个盒子进行排列(即放球),所以完成这件事有4=6720种放法。
(方法二)由于每盒至多放1个球,所以第1个球有8种放法,第2个球有7种放法,…,第5个球有4种放法。
因此,完成这件事有8×7×6×5×4=6720种方法。
模型2(球多盒少)(1)4个不同的球,放入3个不同的盒子,每个盒子至少放1个球,共有多少种放法?(2)6个不同的球放入4个不同的盒子,每个盒子至少放1个球,共有多少种放法?解析(1)这是一个分组和分配的问题,先将4个不同的球分成3组,再进行全排列(即入盒),所以完成这件事有种放法。
两个原理及排列组合经典例题
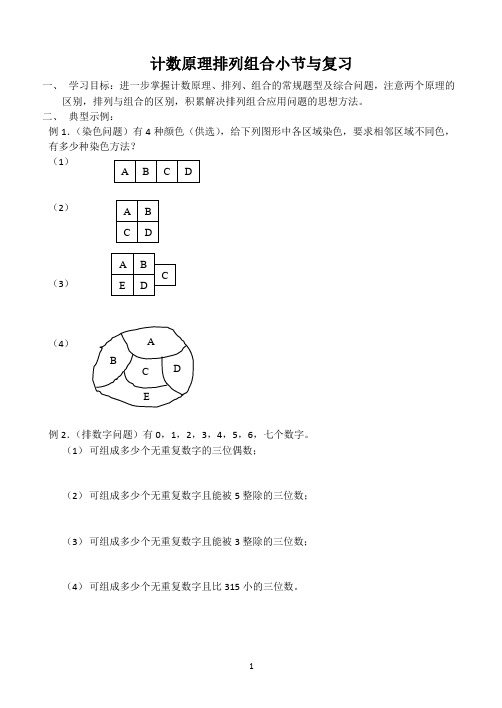
计数原理排列组合小节与复习一、 学习目标:进一步掌握计数原理、排列、组合的常规题型及综合问题,注意两个原理的区别,排列与组合的区别,积累解决排列组合应用问题的思想方法。
二、 典型示例:例1.(染色问题)有4种颜色(供选),给下列图形中各区域染色,要求相邻区域不同色,有多少种染色方法?(1)(2)(3)(4)例2.(排数字问题)有0,1,2,3,4,5,6,七个数字。
(1) 可组成多少个无重复数字的三位偶数;(2) 可组成多少个无重复数字且能被5整除的三位数;(3) 可组成多少个无重复数字且能被3整除的三位数;(4) 可组成多少个无重复数字且比315小的三位数。
例3.(排队照相问题)解决下列问题,掌握解决问题的方法。
(1)7名学生站成一排照相,其中甲不站左端,乙不站右端,有多少种站法?(2)7名学生站成一排照相,其中甲、乙相邻且都与丙不相邻,有多少种站法?(3)7名学生站成一排照相,其中甲、乙在丙的同侧,有多少种站法?(4)7名学生站成一排照相,7人身高各不相同,要求中间高两边低,有多少种站法?(5)8名学生站成两排照相,要求后排4人都比前排对应的4人高,有多少种站法?例4.(小球分配问题)解决下列问题,注意它们的区别并掌握解决问题的方法。
(1)把3个不同的小球放入4个不同的盒子中,有多少种不同放法?(2)把3个不同的小球放入4个不同的盒子中,每个盒子最多放1个,有多少种不同放法?(3)把4个不同的小球放入3个不同的盒子中,有多少种不同放法?(4)把4个不同的小球放入3个不同的盒子中,每个盒子最少放一个,有多少种不同放法?(5)把4个相同的小球放入3个不同的盒子中,每个盒子最少放一个,有多少种不同放法?(7个小球呢?)(6)把4个相同的小球放入3个不同的盒子中,盒子可空,有多少种不同放法?(7)把4个不同的小球放入3个相同的盒子中,有多少种不同放法?三、 补充练习:(1) (2013山东理)用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为( )A .243B .252C .261D .279(2) (2013福建理)满足{},1,0,1,2a b ∈-,且关于x 的方程220ax x b ++=有实数解的有序数对(,)a b 的个数为( )A .14B .13C .12D .10(3) (2013四川理)从1,3,5,7,9这五个数中,每次取出两个不同的数分别为,a b ,共可得到lg lg a b -的不同值的个数是 ( )A .9B .10C .18D .20(4) (2013大纲文)从进入决赛的6名选手中决出1名一等奖,2名二等奖,3名三等奖,则可能的决赛结果共有 种.(用数字作答)(5) (2013上海春)36的所有正约数之和可按如下方法得到:因为2236=23⨯,所以36的所有正约数之和为22(122)(133)91++++=参照上述方法,可求得2000的所有正约数之和为_________.(6) (2013浙江理)将F E D C B A ,,,,,六个字母排成一排,且B A ,均在C 的同侧,则不同 的排法共有________种(用数字作答) .(7) (2013北京理)将序号分别为1,2,3,4,5的5张参观券全部分给4人,每人至少1张,如果分给同一人的2张参观券连号,那么不同的分法种数是_________.(8) (2013大纲理)6个人排成一行,其中甲、乙两人不相邻的不同排法共有_______种.(用数字作答).(9) 以正方体的顶点为顶点的四面体有 个.(10) 如图,用四种不同的颜色给图中的,,,,,A B C D E F 六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法共有________种(用数字作答).四、总结: B C F E D A。
小学数学《排列组合》练习题(含答案)

小学数学《排列组合》练习题(含答案)1、计算①4356C A -;②2265C A ÷。
解答:①4356C A -=5432⨯⨯⨯-654321⨯⨯⨯⨯=120-20=100。
②2265C A ÷5465321⨯=⨯÷=⨯ 2、某班要从30名同学中选出3名同学参加数学竞赛,有多少种选法?如果从30名同学中选出3名同学站成一排,又有多少种站法?解答: 参加竞赛的选法:330302928321C ⨯⨯⨯⨯==4060种 站成一排的站法:330A =30×29×28=24360种参加竞赛的选法有4060种,站成一排的站法有24360种3、7个不同的小球放入4个不同的盒子中,每个盒子只能放一个,一共有多少种情况? 解答:47A =7654⨯⨯⨯=840(种)一共有840种不同的情况。
4、7个相同的小球放入4个不同的盒子中,每个盒子至少放一个,一共有多少种情况? 解答:1+1+1+0=3,1+2+0+0=3,3+0+0+0=3,分三种情况①选出一个盒子,不再放入球,其他三个盒子再各放入一个:14C ;②选出两个盒子,分别再放入一个球,两个球:24A③选出一个盒子,再放入三个球:14C总的放法:14C +24A +14C =20(种)5、从1,3,5,7,9中任取三个数字,从2,4,6,8中任取两个数字,组成没有重复数字的五位数,一共可以组成多少个数?解答:第一步,从1,3,5,7,9中任取三个数字,这是一个组合问题,有35C 种方法; 第二步,从2、4、6、8中任取两个数字,也是一个组合问题,有24C 种方法;第三步,用取出的5个数字组成没有重复数字的五位数,有55A 种方法。
再由分步计数原理求总的个数。
325545A 7200C C ⨯⨯=(个) 一共能组成7200个没有重复数字的五位数。
6、在6名女同学,5名男同学中选出4名女同学,3名男同学站成一排,有多少种排法? 解答:437657A C C ⨯⨯=765000(种)有765000种排法。
排列组合典型问题-分球入盒

分球入盒问题高二数学组朱育璋分球入盒问题(球在盒子的分布情况)是概率中常见的一类题型,如:(1)生日问题:n个人的生日的可能情况(每个人生日是365天之一),相当于n个球放入N=365个盒子中的可能情况(设一年365天);(2)书籍分堆问题: 6 本画册分给 3 份,每份至少一本(3)名额分配问题:7 个参赛名额分给不同班级(4)有n 封信随机的投放在N 个信筒中(筒内信数不限);此类问题具有背景丰富,应用广泛等特点。
本文旨在总结解此类题的规律,理清思路,以便更好的更快的求解问题。
例题分析【例1】按下列要求分配6个不同的小球,各有多少种不同的分配方式(1)分成三份, 1 份1 个,1 份2个, 1 份3个;(2)甲、乙、丙三人中,一人得 1 个,一人得2个,一人得3个;分析:(1)为典型无序分组问题,可分三步完成,即拿出一个做第一份,拿出2个做第二份,拿出3个做第三份,完成分组,对于(2)为有序分组问题,可采取先按(1)分组,再进行分配,即排列。
归纳:从1,2 问区分分组要求与分配要求,并掌握基本方法。
另外,举出类似问题,一起归结为:不同小球投入相同的盒子,不同小球投入不同的盒子(3)分成三份, 1 份 4 个,另外两份每份 1 个;(4)甲、乙、丙三人中,一人得4个,另外两人每人得 1 个;分析:(3 )与( 1 )问题类型相同,同为分组要求,不同的地方:出现两份小球数目一样,即有均分组,此时按原方法计算会导致重复计算,举例:不妨记6个球为A、B、 C D E、F,若第一步取了ABCD第二步取了E,第三步取了F,记该种分法为(ABCD,E,F),则同样分法中还有(ABCD,F,E),共2种情况,而这2种情况仅是E,F的顺序不同,从排列角度易算出不同的分法为A22,需在原基础上除以A22,消去顺序。
归纳:在分组中出现均分组情况,需要消序,即除以均分组的组数全排列数【例2】按下列要求分配 6 个相同的小球,各有多少种不同的分配方式(1)分成三份, 1 份1 个,1 份2个, 1 份3个;(2)甲、乙、丙三人中,一人得 1 个,一人得2个,一人得3个;一.(1)通过穷举的办法算出结果,认识到分法差异在于各组小球数量的相对性二.(2)分法差异在于不同的小组小球的数量,方法:先定数量分配,再分配入盒。
专题十一:隔板法在解排列组合问题中的应用(同元分组问题)

隔板法在解排列组合问题中的应用隔板法又称隔墙法、插板法是处理名额分配、相同物体的分配等排列组合问题的重要方法,本文将将通过例题将这种方法作以介绍,供同学们学习时参考.一、将n 件相同物品(或名额)分给m 个人(或位置),允许若干个人(或位置)为空的问题例1将20个大小形状完全相同的小球放入3个不同的盒子,允许有盒子为空,但球必须放完,有多少种不同的方法?分析:本题中的小球大小形状完全相同,故这些小球没有区别,问题等价于将小球分成三组,允许有若干组无元素,用隔板法.解析:将20个小球分成三组需要两块隔板,将20个小球及两块隔板排成一排,两块隔板将小球分成三块,从左到右看成三个盒子应放的球数,每一种隔板与球的排法对应一种分法.将20个小球和2块隔板排成一排有22个位置,先从这22个位置中取出两个位置放隔板,因隔板无差别,故隔板之间无序,是组合问题,故隔板有222C 种不同的放法,再将小球放入其他位置,由于小球与隔板都无差别,故小球之间无序,只有1种放法,根据分步计数原理,共有222C ×1=231种不同的方法.点评:对n 件相同物品(或名额)分给m 个人(或位置),允许若干个人(或位置)为空的问题,可以看成将这n 件物品分成m 组,允许若干组为空的问题.将n 件物品分成m 组,需要1m -块隔板,将这n 件物品和1m -块隔板排成一排,占1n m +-位置,从这1n m +-个位置中选1m -个位置放隔板,因隔板无差别,故隔板之间无序,是组合问题,故隔板有11m n m C -+-种不同的方法,再将物品放入其余位置,因物品相同无差别,故物品之间无顺序,是组合问题,只有1种放法,根据分步计数原理,共有11m n m C -+-×1=11m n m C -+-种排法,因1m -块隔板将n 件相同物品分成m 块,从左到右可以看成每人所得的物品数,每一种隔板与物品的排法对应于一种分法,故有11m n m C -+-种分法.二、将n 件相同物品(或名额)分给m 个人(或位置),每人(或位置)必须有物品问题例2将20个优秀学生名额分给18个班,每班至少1个名额,有多少种不同的分配方法?分析:本题是名额分配问题,用隔板法.解析:将20个名额分配给18个班,每班至少1个名额,相当于将20个相同的小球分成18组,每组至少1个,将20个相同的小球分成18组,需要17块隔板,先将20个小球排成一排,因小球相同,故小球之间无顺序,是组合,只有1种排法,再在20个小球之间的19个空档中,选取17个位置放隔板,因隔板无差别,故隔板之间无序,是组合问题,故隔板有1719C 种不同的放法,根据分步计数原理,共有1719C 种不同的方法,因17块隔板将20个小球分成18组,从左到右可以看成每班所得的名额数,每一种隔板与小球的排法对应于一种分法,故有11m n m C -+-种分法.点评::对n 件相同物品(或名额)分给m 个人(或位置),每个人(或位置)必须有物品问题,可以看成将这n 件物品分成m 组,每组不空的问题.将n 件物品分成m 组,需要1m -块隔板,将这n 件物品排成一排,因物品无差别,故物品之间无顺序,是组合问题,只有1种排法,再在这n 件物品之间的1n -空档中选取1m -个位置放隔板,占1n m +-位置,从这1n m +-个位置中选1m -个位置放隔板,因隔板无差别,故隔板之间无序,是组合问题,故隔板有11m n C --种不同的放法,根据分步计数原理,共有1×11m n C --=11m n C --种不同排法,因1m -块隔板将n 件相同物品分成m 块,从左到右可以看成每人所得的物品数,每一种隔板与物品的排法对应于一种分法,故有11m n C --种分法.对相同物品分配问题,注意某若干组能否为空,能为空和不能为不空,方法不同,要体会和掌握.。
数学教学:浅谈排列组合中的“球入盒”问题

数学教学:浅谈排列组合中的“球入盒”问题作者:蔡丽菊来源:《数学大世界·中旬刊》2019年第08期在高中数学中有《排列组合》这一章,对学生逻辑推理能力、分类讨论以及建构模型的能力都有极高的要求,包括现在的数学竞赛中都涉及排列组合问题。
其中,“小球与盒子”的模型问题一直是一个热门话题。
由于球与盒子都有着“相同”与“不同”的分类,并且具有知识上的综合性、解题技巧上的灵活性以及思维方式上的抽象性,使同学对此类问题感到很是困惑,感觉千变万化,无从下手。
下面我就对此模型问题的解法及运用作一个总结和分析,望同学有所感悟。
类型一:不同小球入不同盒子的模型1.球少盒多型例1:若将4个不同的小球,放入5个不同的盒子里,有几种不同的放法?解:分四步完成,每一个小球都有5种放法,所以共有种不同的放法。
变式1:若将4个不同的小球,放入5个不同的盒子里,每盒至多放一个,有几种不同的放法?解:与例1相比,这次把盒子看成元素,即从5个不同的盒子里任意取出4个盒子,来放4个不同的小球,所以这是个排列问题。
有种不同的方法。
变式2:若将5个不同的小球,放入5个不同的盒子里,每盒至少放一个,有几种不同的放法?解:此题是5个不同小球的全排列问题,所以有种不同的方法。
注:此类问题一般用排列组合思想,利用分步计数原理2.球多盒少且每盒至少放一球型例2:若将5个不同的小球,放入4个不同的盒子里,每盒至少放一个,有几种不同的放法?解:分两步完成,先将5个小球先分成4组,根据题意,每组分别是2个、1个、1个、1个,有种方法;然后再将分成4组的小球放到4个不同的盒子里,相当于全排列,即有种方法,所以共有种不同的方法。
变式:若将5个不同的小球放入4个不同的盒子里,恰有1个空盒,有几种不同的放法?解:分三步完成。
第一步,选1个空盒,有种不同的方法;类型二:相同小球放入不同盒子的模型例3:若将10个相同的小球,放入3个不同的盒子里,每个盒子不空,有多少种不同的放法?解:此类问题可以用隔板法解决,即在10个小球中间的9个空中放两个相同隔板的问题,自然分成3组,代表放入三个不同盒子中,故有种方法。
微专题 隔板法解排列组合问题

微专题 “隔板法”模型的构建与应用隔板法隔板法是将n 个相同元素分成m 组(每组的任务不同),求不同分法种数的一种解题方法。
利用隔板法能够巧解许多排列、组合问题.(1)当每组至少含一个元素时,其不同分组方式有11--m n C 种,即给n 个元素中间的(1-n )个空隙中插入(1-m )个隔板.(2)任意分组,可出现某些组含0个元素的情况,其不同分组方式有11--+m m n C 种,即将n 个相同元素与(1-m )个相同隔板进行排序,在(1-+m n )个位置中选(1-m )个安排隔板.典例解析题型一:每盒非空例1.将10个相同的小球分别装入3个不同的盒子中且每盒非空(即每盒至少放入1个小球),有 种不同的装法.解析:将10个小球排成一排,在其两两之间的9个空位中任意取两个划上竖线,这样就将10个小球分成了3组.图1-1所示的是其中一种装法.图11-将每组小球按顺序装入3个盒子中,则划竖线的方法数等于题中所求的装法数,装法共有3629=C (种).例2.求方程1x +2x +…+5x =7的正整数解的个数.解析:用7个相同的小球代表数7, 用5个标有1x 、2x 、…、5x 的5个不同的盒子表示未知数1x 、2x 、…、5x ,要得到方程1x +2x +…+5x =7的正整数解的个数.可分以下两步完成:第一步:从7个相同的小球中任取5个放入5个不同的盒子中,仅有1种放法; 第二步:把剩余的2个小球放入5个不同的盒中,由隔板法知,此时有46C 种放法.由分步计数原理知,共有46C 种不同放法.我们把标有i x (i=1,2,…,5)的每个盒子得到的小球数i k (i=1,2,…,5; i k N ∈+),记作:i x =i k .这样,将7个相同的小球放入5个不同的盒子中的每一种放法,就对应着方程1x +2x +…+5x =7的每一组解(1k ,2k ,…,5k ).46C =26C =1256⨯⨯=15(个) 所以,方程1x +2x +…+5x =7的正整数解共有15个.点评:准确理解隔板法的使用条件,是使用隔板法求方程1x +2x +…+5x =7的非负(或正)整数解的个数的理论依据.题型二:每盒至少有n 个例3.将20本练习本分给4名学生,要求每名学生至少得3本,有 种不同的分法.解析:首先分给每人2本练习本,然后将剩下的12本练习本按例1中划竖线的方法分给4名学生,这样每人就至少得3本练习本,所以不同的分法共有(种)165311=C .题型三:每盒分别有m n n n ,,,21 个例4.将20个相同的小球全部放入编号为3,4,5的三个盒子中,要求每个盒子内的球数不少于它的编号数,则不同的放法有 种.解析:首先在三个盒子中依次放入2,3,4个球,再将剩余的11个球按例1中划线的方法分到三个盒子中,这样就能满足“每个盒内的球数不少于它的编号数”的要求.于是不同的放法共有(种)45210=C题型四:每盒可空例5.把8个相同的球放入4个不同的盒子,有多少种不同方法?解析:取3块相同隔板,连同8个相同的小球排成一排,共11个位置.由隔板法知,在11个位置中任取3个位置排上隔板,共有C 311种排法.311C =12391011⨯⨯⨯⨯=165(种) 所以,把8个相同的球放入4个不同的盒子,有165种不同方法.点评:相同的球放入不同的盒子,每个盒子放球数不限,适合隔板法.隔板的块数要比盒子数少1.例6.求10521)(x x x +⋅⋅⋅++展开式中共有多少项?解:用10个相同的小球代表幂指数10, 用5个标有1x 、2x 、…、5x 的5个不同的盒子表示数1x 、2x 、…、5x ,将10个相同的小球放入5个不同的盒子中,把标有i x (i=1,2,…,5)每个盒子得到的小球数i k (i=1,2,…,5; i k N ∈),记作i x 的i k 次方.这样,将10个相同的小球放入5个不同的盒子中的每一种放法,就对应着展开式中的每一项.由隔板法知,这样的放法共有414C 种,故10521)(x x x +⋅⋅⋅++的展开式中共有414C 项。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小球入盒模型的推广应用
摘要:小球入盒是排列组合的典型问题,本文从小球同与不同及盒子同与不同几方面对小球入盒模型的加以推广应用。
小球入盒是排列组合的典型问题,与之相关的有名额分配、人员分配等问题,形式多样.“小球入盒问题”问题可以分为四类:不同的小球放入不同的盒子里;不同的小球放入相同的盒子里;相同的小球放入不同的盒子里;相同的小球放入相同的盒子里(此类不做重点讨论)。
解答小球入盒问题的最有效、最易于操作的方法是“先分组后分配”,即先将元素分组、再分配到位置.分组时应注意平均分组与非平均分组的区别;放入相同盒子可看作分组无分配问题;解答相同小球入不同盒子问题的最有效、最易于操作的方法是隔板法。
【引例】
①把4个相同的小球放入3个相同的盒子,共有多少种不同的放法
②把4个不同的小球放入3个不同的盒子,共有多少种不同的放法
③把4个不同的小球放入3个相同的盒子,共有多少种不同的放法
④把4个相同的小球放入3个不同的盒子,共有多少种不同的放法
【解析】①由于小球相同,盒子也相同,故小球数目的不同分组就对应不同的放法,小球数目分组有4+0+0型、3+1+0型、2+2+0型、2+1+1型,故只有4种放法.
②(乘法原理)分4步,把小球一个一个地放入盒子,每一个小球都有3种放法,由乘法原理,共有种放法.
③(先分组后分配)先将不同小球分为三组,有4+0+0型(种方法)、3+1+0型(种方法)、2+2+0型(种方法)、2+1+1型(种方法),共14 种分组方法,再将三组小球分配到三个盒子,由于盒子相同,故都只有1种方案,故共有14 种放法.
④法1:(先分组后分配)先将小球分为三组,有4+0+0型、3+1+0型、2+2+0型、2+1+1型,
由于小球相同,故各只有1种分组方法;再将三组小球分配到三个盒子,由于盒子不同,故有种放法.
法2:(隔板法)每种放法对应于将4个相同小球与2个相同“隔板”进行的一次排列,即从6个位置中选2个位置安排隔板,故共有 =15种放入的方式。
一. n个相同的小球放入m个不同的盒子模型
在排列组合中,对于将不可分辨的球装入到可以分辨的盒子中而求装入方法数的问题,常用隔板法。
模型1 将n个相同的小球放入编号分别为1,2,3,4,…,m的m个盒子中(m≤n),每个盒子中至少有一个小球的不同放法总数为。
【解析】n个相同小球串成一串从n-1个间隙里选m-1个结点剪成m段(或者看作插入m-1块隔板),有种方法.
模型2 将n个相同的小球放入编号分别为1,2,3,4,…,m的m个盒子中(m≤n),每个盒子可空的放法总数为。
【解析】任意分组,可出现某些组含元素为0个时,其不同分组方式为:m个盒子排成一行,中间有m-1块隔板,把n个球放入m个盒子,不同的放法对应着n个球和m-1块隔板的不同排列,于是在n+m-1个位置中选m-1个位置安排隔板,所以放法总数为。
模型3 将n个相同的小球放入编号分别为1,2,3,4,…,m的m个盒子中(m≤n),要求每个盒子中的球数不少于它的编号数的放法总数为。
【解析】法1:先在编号1,2,3,4,…,m的m个盒子内分别放0,1,2,3,4,…,m-1个球,剩下个球分成m组,每组至少1个,由模型1方法知有(种)方法。
法2:第一步先在编号1,2,3,4,…,m的m个盒子内分别放1,2,3,4,…,m个球,剩下个球放入m个盒子,不同的放法对应着个球和m-1块隔板的不同排列,于是在个位置中选m-1个位置安排隔板,有(种)方法。
隔板法:将放有小球的盒子紧挨着成一行放置,便可看作成一行的小球的空隙中插入了若干隔板,相邻两块隔板形成一个“盒”.每一种插入隔板的方法对应着小球放人盒子的一种方法,此法称为隔板法.隔板法专门解决相同元素的分配问题.
应用1(求不定方程整数解)
1.不定方程的正整数解的个数为。
【解析】可看作n个相同的小球放入m个不同盒子中,要求每个盒子不空时球的放法数,于是将n个小球排成一行,它们形成n-1个空挡,只插m-1个隔板,故有种方法。
2.不定方程的非负正整数解的个数为。
【解析】可看作n个相同的小球放入m个不同盒子中,要求每个盒子可空时球的放法数,由模型2知非负正整数解的个数为。
应用2(多项式定理中展开式项数问题)
3.三项式展开式共有多少不同的项
【解析】的展开式中每一项的指数和均是 n,相当于 n个无区别的球放入、、三个不同的盒子里,每个盒放入的球数不限,由模型2知为展开式中共有不同的项数为。
应用3(名额分配问题)
4.将10个优秀的指标分配给3个班级,
(1)每班至少一个,则共有多少种分配方法
(2)任意分配共有多少种分配方法
(3)若班级为一、二、三班,若名额数不小于班级数,则共多少种分配方法
【解析】:由于10个优秀指标是相同的,该题等价于10个相同的小球放入3个不同盒子模型。
可采用“隔板法”。
(1)插隔板,即9个空格中插入2个隔板,共有种分配方法。
(2)排隔板,即10个指标和2个隔板,共12个位置选2个放隔板,共有种分配方法。
(3)先给一班0个优秀名额,二班1个优秀名额,三班2个优秀名额,再对剩下的7个优秀名额用插隔板法,共有种分配方法。
总之,凡是处理与“相同元素有序分组”模型时,我们都可采用“隔板法”。
若每组元素数目至少一个时,可用插“隔板”,若出现每组元素数目为0个时,可用排“隔板”。
二.n个不同的小球放入m个不同的盒子模型
模型4. 把n个不同的小球放入m个不同的盒子,有多少种不同放法
【解析】每个小球有m种放法,共有种放法。
模型5. 把n个不同的小球放入m个不同的盒子,每盒放球不超过1个,直至球放完或盒子放满为止,有多少种不同放法
【解析】(1)若n>m,将n个小球当做n个元素,这样问题实质即在n个元素中取m个元素的排列问题,有种。
(2)若n<m,将m个小盒当做m个不同元素,这样问题实质即在m个元素中取n个元素的排列问题,有种。
(3)若n=m, 有 ==n!
模型6. 在n个不同的小球中取m个放入m个不同的盒子中,每盒只放一个,其中某一个小球必须放在某一个指定的盒子中,有多少种不同的放法
【解析】先将某一个小球放在指定的盒子中,然后从剩下的n-1个不同的小球中任取m-1个,放入m-1个不同的小盒中,共有种放法。
模型7 在n个不同的小球中取m个放入m个不同的盒子中(m<n),每盒只放一个,其中某一个小球不能放在某一个指定的盒子中,有多少种不同的放法
【解析】第一类:某一小球没有取到,则从n-1个小球中取出m个小球放入m个盒子中,共有种;第二类:某一小球被取到,它只能被放到指定小盒以外的m-1个盒子中。
第一步放指定小球有m-1种,第二步从n-1个小球中取m-1个放入剩下的m-1个盒子中,有种,所以有种。
综上共 +种放法。
应用4. (1) 5本不同的书全部送给6人,每人至多1本,有多少种不同的送书方法
(2)6本不同的书送给5人,每人至多1本,有多少种不同的送书方法
(3)6本不同的书送给5人,每人至少1本,有多少种不同的送书方法
(4)6本不同的书送给5人,每人1本,且其中一本《麻将技巧》不能送给小学生章子怡,则有多少种不同的送书方法
【解析】(1)相当于5个不同小球放入6个不同的盒子中,每盒至多一球,所以有种不同送书方法。
(2)相当于6个不同小球放入5个不同的盒子中,每盒至多一球,所以有种不同送书方法。
(3)第一步先将6本书分成5堆,其中一堆2本书,有种方法,第二步把5堆书分给5个人,有种方法,所以共有1800种不同送书方法.(4)第一类:《麻将技巧》没送出,有种方法;第二类:《麻将技巧》送给章子怡以外的4人中某一人,有4种方法;然后从剩下的5本书中取4本送另外4个人,有种方法,所以有480种方法;综上,知有120+480=600种方法.
应用5. 四位选手争夺三个运动项目的金牌,则有多少不同的金牌结果种数
【解析】可看作3个不同小球放在4个不同盒子中的放法,共种结果。
三.n个不同的小球放入m个相同的盒子模型
模型8. n个不同的小球放入m个相同的盒子可看作将n个元素分成m组无分配的分法种数,我们有下面的结论:
(1)若k1+ k2+ k3+ ……+km=n且k1,k2,k3,……km互不相等,
则将n个元素分成m个组(其中第一个组k1个元素,第二个组k2个元素,第m个组km个元素)的不同分法种数为
(2)若将n个元素平均分成m个组,每组k个元素(n=mk),则所有不同的分法种数为
(3)一般地,n个不同的元素分成m组,各组内元素数目分别为k,k,…,,其中h组内元素数目相等,那么分组方案是。
应用6. 6本不同的书(6个不同的小球)分成4组(放入4个相同盒子,每盒不空),有多少种不同的分法
【解析】先将不同小球分为4组,有3+1+1+1型(种方法)、2+2+1+1型(种方法),共 +=65种分组方法,再将4组小球分配到4个盒子,由于盒子相同,故都只有1种方案,故共有65 种放法.。
