1-6极限存在准则PPT课件
合集下载
1-6函数极限

| 2x 1 | 2 | x | 1 | x |
x1 1 3 1 3 1 3 2x 1 2 2 |2x 1| 2| x | | x |
0 要使 x 1 1
2x 1 2
只须 | x | 1和 | x | 3同时成立
令X max{1, 3} 则当 | x | X时,便有
( x x0 )
右极限 0, 0,使当x0 x x0 时,
恒有 f (x) A .
记作 lim f ( x) A 或
x x0 0
(
x
x
0
)
注意 :{x 0 x x0 }
f ( x0 0) A.
{ x 0 x x0 } { x x x0 0}
定理 : lim x x0Fra bibliotekf (x)
A
f (x0
0)
f (x0
0)
A.
例6 验证 lim x 不存在. x0 x
y
证 lim x lim x x0 x x0 x lim (1) 1
x 0
1
o
x
1
lim x lim x lim 1 1
x1 1 3 1 2x 1 2 2 |2x 1|
3
|x|
lim x 1 1 n 2 x 1 2
定义 : 如果lim f ( x) c,则直线 y c是函数y f ( x) x
的图形的水平渐近线.
二、自变量趋向有限值时函数的极限
先看一个例子 考察x 1时,函数f ( x) 2( x2 1)的变化趋势
定理(保号性) 若 lim f ( x) A,且A 0(或A 0), x x0
1-6 两个重要极限

n n2 1 n2 2
n2 n
2.单调有界准则
如果数列 xn满足条件 x1 x2 xn xn1 , 单调增加 x1 x2 xn xn1 , 单调减少
单调数列
几何解释:
x1 x2 x3xn xn1 A M
x
二、两个重要极限
证:
当
x(0,
π 2
)
时,
△AOB 的面积< 圆扇形AOB的面积
•
7、最具挑战性的挑战莫过于提升自我 。。20 20年12 月上午 12时31 分20.1 2.1000: 31Dece mber 10, 2020
•
8、业余生活要有意义,不要越轨。20 20年12 月10日 星期四 12时31 分35秒 00:31:3 510 December 2020
•
9、一个人即使已登上顶峰,也仍要自 强不息 。上午 12时31 分35秒 上午12 时31分 00:31:3 520.12. 10
x0 x
(2) lim sin 5x x0 sin 8x
(4) lim
x0
1
cos x2
x
arcsin x
(5) lim
x0
x
(3) lim tan x x0 x
(6) lim sin x x x
说明:1. 以下结论也可直接作为公式使用
lim tan u 1 u0 u lim arcsin u 1 u0 u
• 10、你要做多大的事情,就该承受多大的压力。12/10/
2020 12:31:35 AM00:31:352020/12/10
• 11、自己要先看得起自己,别人才会看得起你。12/10/
谢 谢 大 家 2020 12:31 AM12/10/2020 12:31 AM20.12.1020.12.10
高等数学课件同济六版上册1-6

法2 找两个趋于
n
, 使 的不同数列 xn 及 xn
n
) lim f ( xn ) lim f ( xn
例1. 证明
不存在 .
证: 取两个趋于 0 的数列 1 1 xn 及 xn 2n 2n 2 有
(n 1, 2 ,)
1 lim sin lim sin 2n 0 n xn n 1 lim sin lim sin(2n ) 1 2 n n xn
x
x lim (1 1 ) e x
当
时, 令 x (t 1) , 则
1 ) (t 1) lim (1 t 1 t
从而有
t ) (t 1) 1) t 1 lim ( t lim ( 1 1 t t t t 1)] e lim [(1 1 ) ( 1 t t t
定理1. lim f ( x) A
x x0 ( x )
xn x0 , f ( xn ) 有定义
有 lim f ( xn ) A .
n
且
( xn )
Note: 此定理常用于判断函数极限不存在 .
法1 找一个数列
n
xn x0 ,
使 lim f ( xn ) 不存在 .
( x )
原式 lim (1
x
1 ) x 1 x
e 1
例7. 求
解: 原式 =
1 ) 2 ]2 lim [(sin 1 cos xx x x 2x
lim (1 sin 2 ) x
x
(1 sin 2 ) x
1 sin 2 x
m 7. lim 1 _____ x x
n
, 使 的不同数列 xn 及 xn
n
) lim f ( xn ) lim f ( xn
例1. 证明
不存在 .
证: 取两个趋于 0 的数列 1 1 xn 及 xn 2n 2n 2 有
(n 1, 2 ,)
1 lim sin lim sin 2n 0 n xn n 1 lim sin lim sin(2n ) 1 2 n n xn
x
x lim (1 1 ) e x
当
时, 令 x (t 1) , 则
1 ) (t 1) lim (1 t 1 t
从而有
t ) (t 1) 1) t 1 lim ( t lim ( 1 1 t t t t 1)] e lim [(1 1 ) ( 1 t t t
定理1. lim f ( x) A
x x0 ( x )
xn x0 , f ( xn ) 有定义
有 lim f ( xn ) A .
n
且
( xn )
Note: 此定理常用于判断函数极限不存在 .
法1 找一个数列
n
xn x0 ,
使 lim f ( xn ) 不存在 .
( x )
原式 lim (1
x
1 ) x 1 x
e 1
例7. 求
解: 原式 =
1 ) 2 ]2 lim [(sin 1 cos xx x x 2x
lim (1 sin 2 ) x
x
(1 sin 2 ) x
1 sin 2 x
m 7. lim 1 _____ x x
高等数学1-6极限存在准则,两种重要极限

n
xn a 成立,
该准则可以推广到函数的极限
准则 I'
如果当 x U ( x0 ) (或 | x | M )时,有
(1) g( x ) f ( x ) h( x ),
(2) lim g ( x ) A,
x x0 ( x ) x x0 ( x )
o
lim h( x ) A,
lim 那么 x x f ( x ) 存在, 且等于 A .
( x )
0
准则 I 和准则 I’ 称为夹逼准则. 注意: 利用夹逼准则求极限关键是构造出 yn与 zn
( g( x ), h( x )), 并且 yn ( g ( x ))与zn ( h( x )) 的极限
1 x lim (1 ) e . x x
1 x 再证 xlim (1 ) e , x
令 t x,
1 x lim (1 ) e . x x
1 x 1 t t t lim (1 ) lim(1 ) lim( ) x t t t 1 x t 1 t lim(1 ) lim(1 1 )t 1 (1 1 ) e. t t 1 t t 1 t 1 1 令t , x
复习
1. 无穷小与无穷大的定义
2. 无穷小与函数极限的关系 3. 无穷小与无穷大的关系
几点注意:
1. 无穷小和无穷大是相对于过程而言的;
2. 无穷小(大) 是变量,不能与很小(大)的数混淆; 3. 零是唯一可作为无穷小的数; 4. 无界变量未必是无穷大.
1. 极限运算法则
(1) 无穷小运算法则 (2) 极限四则运算法则 (3) 复合函数极限运算法则
arcsin x . 例5. 求 lim x 0 x
xn a 成立,
该准则可以推广到函数的极限
准则 I'
如果当 x U ( x0 ) (或 | x | M )时,有
(1) g( x ) f ( x ) h( x ),
(2) lim g ( x ) A,
x x0 ( x ) x x0 ( x )
o
lim h( x ) A,
lim 那么 x x f ( x ) 存在, 且等于 A .
( x )
0
准则 I 和准则 I’ 称为夹逼准则. 注意: 利用夹逼准则求极限关键是构造出 yn与 zn
( g( x ), h( x )), 并且 yn ( g ( x ))与zn ( h( x )) 的极限
1 x lim (1 ) e . x x
1 x 再证 xlim (1 ) e , x
令 t x,
1 x lim (1 ) e . x x
1 x 1 t t t lim (1 ) lim(1 ) lim( ) x t t t 1 x t 1 t lim(1 ) lim(1 1 )t 1 (1 1 ) e. t t 1 t t 1 t 1 1 令t , x
复习
1. 无穷小与无穷大的定义
2. 无穷小与函数极限的关系 3. 无穷小与无穷大的关系
几点注意:
1. 无穷小和无穷大是相对于过程而言的;
2. 无穷小(大) 是变量,不能与很小(大)的数混淆; 3. 零是唯一可作为无穷小的数; 4. 无界变量未必是无穷大.
1. 极限运算法则
(1) 无穷小运算法则 (2) 极限四则运算法则 (3) 复合函数极限运算法则
arcsin x . 例5. 求 lim x 0 x
高等数学1-6 同济第六版

2π
例4. 已知圆内接正 n 边形面积为
n
2π sin n 证: lim An lim πR 2 n 2π n n
证明:
R
注: 计算中注意利用
( x ) 0 重要 !
三、单调有界数列的收敛准则
准则II :单调有界数列必有极限。
若数列{xn}满足 x1 x2 x3 xn xn1
t 1 t t
x
e
x 1 x 1 x 故 lim (1 1 ) e ( 因 lim ( 1 ) lim ( 1 x x x) e )
x
x
例5.
解: 令 t x , 则
1 t lim (1 ) t t 1 lim
t
几何平均值 算术平均值
n
a1 a2 an a1 a2 an n
Cauchy不等式
第二步, 证明数列{xn}有界.
1 1 1 n 1 1 1 1 1 xn (1 ) (1 ) (1 )(1 ) 4 4 n 2 2 n n n
( 形如1 的情形要注意用此极限并 “凑”成标准型 )
课堂练习
求极限:
作业
P56-57
1/(2)(3)(4)(6)
2
4/(2)(3)
提示:利用单调有界数列有极限证明。 先用归纳法证明有界, 再证明单调。
下页有思考题.
思考题
(中科院2001硕士入学考题)
(研1996 )
ε 0, 正整数 N 1 , 当n N 1 时, | yn a | ε. ε 0, 正整数 N 2 , 当n N 2 时, | zn a | ε.
例4. 已知圆内接正 n 边形面积为
n
2π sin n 证: lim An lim πR 2 n 2π n n
证明:
R
注: 计算中注意利用
( x ) 0 重要 !
三、单调有界数列的收敛准则
准则II :单调有界数列必有极限。
若数列{xn}满足 x1 x2 x3 xn xn1
t 1 t t
x
e
x 1 x 1 x 故 lim (1 1 ) e ( 因 lim ( 1 ) lim ( 1 x x x) e )
x
x
例5.
解: 令 t x , 则
1 t lim (1 ) t t 1 lim
t
几何平均值 算术平均值
n
a1 a2 an a1 a2 an n
Cauchy不等式
第二步, 证明数列{xn}有界.
1 1 1 n 1 1 1 1 1 xn (1 ) (1 ) (1 )(1 ) 4 4 n 2 2 n n n
( 形如1 的情形要注意用此极限并 “凑”成标准型 )
课堂练习
求极限:
作业
P56-57
1/(2)(3)(4)(6)
2
4/(2)(3)
提示:利用单调有界数列有极限证明。 先用归纳法证明有界, 再证明单调。
下页有思考题.
思考题
(中科院2001硕士入学考题)
(研1996 )
ε 0, 正整数 N 1 , 当n N 1 时, | yn a | ε. ε 0, 正整数 N 2 , 当n N 2 时, | zn a | ε.
1-6.极限的性质
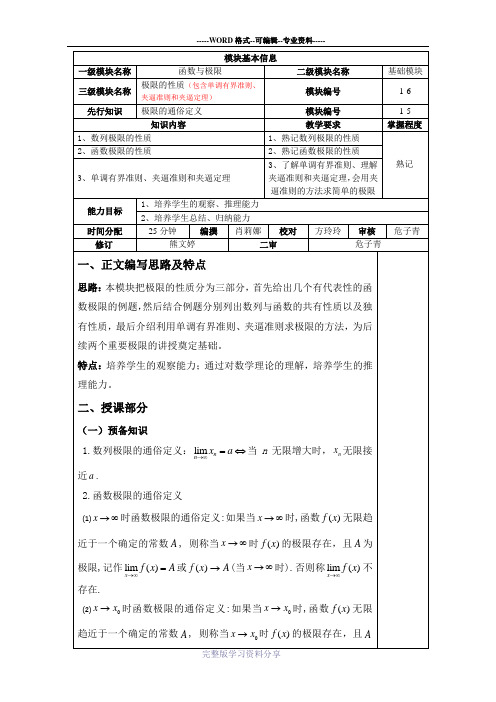
为极限,记作0
lim ()x x f x A →=或A x f →)((当0x x →时).否则称
lim ()x x f x →不存在.
(二)新课讲授 1. 函数极限的例题
考虑下列数列与函数的极限 当∞→n 时,
⑴ ;1+=n n x n ⑵ 1(1);2
n
n x +-=
以及 ⑶ ;1
lim
+∞→x x
x ⑷ .lim 0x x x →
2. 数列与函数的共有性质以及独有性质
⑴ 共有性质
根据11lim =+∞→n n n 、11lim =+∞→x x
x 、2
)1(1lim
n n -+∞→不存在以及x x x 0lim → 不存在,可得以下性质:
定理1 (数列极限的唯一性) 若数列{x n }收敛,则极限是唯一的.
例如:数列()112n
⎧⎫-+⎪⎪
⎨⎬⎪⎪⎩⎭
,当n 无限增大时,数列分别趋近于0和
1,因此该数列无极限.
定理2 (函数极限的唯一性) 如果极限)(lim 0
x f x x →存在, 那么这极限
唯一.
例如:由于0
0lim 1,lim 1x x x x x
x +
-→→==-,则0lim x x x →无极限.
注:定理1和定理2常被用在证明数列极限和函数极限的不存在性上. 根据11lim =+∞→n n n ,011n n <<+,即{1
n
n +}有界.
定理3 (收敛数列的有界性) 如果数列{x n }收敛, 那么数列{x n }一
5,n x =+2
1
n ⎫
+
+21n +
⎪+⎭
.。
1.6 极限存在准则

9
例4 证明:(1) lim(1 1 )n e; (2) lim(1 1 )x e
n
n
x
x
证 (1) 设
xn
1
1 n
n
,
yn
1
1 n
n1
a1a2
an1
a1
a2 n
1
an1
n1
(ai 0)
xn
1
1 2
n2
1 n
1 n2
2 n
2
L
n2
n n
n
所以
1 2 L n n (n 1) / 2 n2 n 1 n 2 n 1
lim
n
n
2
1 n
1 n2
2 n
L 2
4
定理1.6.2(函数的两边夹准则) 设函数f(x),g(x),h(x)满足条件
Table[N[(1 + 1/n)^n, 20], {n, 1000, 10000, 1000}] 运行得:
{2.7169239322358924574,2.7176025693231394203,
2.7178289198746224552, 2.7179421210793585709,
2.7180100501018540468, 2.7180553395755901871,
(1)g( x) f ( x) h( x),x U 0( x0 ) (或 x X ) (2)lim g( x) A,lim h( x) A 则函数f (x)的极限存在,且有 lim f (x) A。 其中极限趣向,可以是任何情形。
高等数学1.6极限存在准则、两个重要极限

二、两个重要极限
例4
1 cos x 求 lim . 2 x0 x
2 x x 2 sin 2sin 2 1 lim 2 解 原式 lim 2 x 0 2 x x 0 x 2 2 2
0 0
sin x lim 1 x 0 x
lim cos x 1,
x 0
x x0 x x0
lim f ( u ) A, 则 lim f [ g ( x )] A lim f ( u )
u a
证明
lim(1 x ) e
x 0
1 x
x x0 1 x
u a
1 1 令 x , lim(1 )t = lim(1 x ) t t t x0
x x0 ( x ) x x0 ( x )
f ( x) lim h( x ) A, 那末 xlim x
( x)
0
存在, 且等于 A 上述两准则称为两边夹准则.
例1 求 lim( n 解:
1 n 1
2
1 n 2
2
1 n n
2
).
n n n
2
n
x 1 sin x 1, cos x 1 sin x cos x x
A
下面证 lim cos x 1,
x0
2 x x x 2 2 1 cos x 2 sin 2( ) , 2 2 2
0 cos x 1 x2 lim 0, lim(1 cos x ) 0, x0 x0 2 sin x lim cos x 1, lim1 1, lim x 0 x0 x0 x
(2)
1 x lim (1 ) e x x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
lim n
xn
a.
上述数列极限存在的准则可以推广到函数的极限
内蒙古工业大学
3
贾永旺
Advanced Mathematics
准则Ⅰ′
如果当
x
U
0
(
x 0
)
(或
x
M )时,有
(1) g( x) f ( x) h( x),
(2) lim g( x) A, lim h( x) A,
x x0 ( x )
并且 yn与 zn的极限是容易求的 . (2).此准则对于x 时的情形也成立
夹逼定理示意图
g( x) f ( x) h( x)
A
内蒙古工业大学
5
贾永旺
Advanced Mathematics
例1 求 lim( 1 1 1 ).
n n2 1 n2 2
n2 n
解
n n2 n
1 n2 1
Advanced Mathematics
§1.6 极限存在准则 两个重要极限
本节将给出两个在后面求极限时经常要用到的重 要的极限公式:
lim sin x 1 x0 x
li
内蒙古工业大学
1
贾永旺
Advanced Mathematics
一、极限存在准则
2
2
1 13
lim n
xn
2
.
内蒙古工业大学
8
贾永旺
Advanced Mathematics
二、两个重要极限
(1) lim sin x 1 x0 x
首先注意到 函数 sin x 对一切x 0都有定义
x
sin x
设法构造一个“夹逼不等式”,使函数 x
在x=0的某去心邻域内置于具有同一极限值的两个
1 n2 n
n ,
n2 1
又 lim n
n lim n2 n n
1 1 1 1,
n
n
1
lim
n
lim n2 1 n
1,
1
1 n2
由夹逼定理得
lim( 1 1 1 ) 1.
n n2 1 n2 2
n2 n
内蒙古工业大学
6
贾永旺
Advanced Mathematics
2.单调有界准则
x2
2 sin 2
lim
x0
x2
1
sin lim(
.
x 2
x 2)
1 lim
sin 2
x 2
2 x0 ( x)2
2
2 1 12 1 .
2 x0 x
2
2
2
例4
求
lim
x0
tan
x x3
sin
x
解
原式
lim
x0
sin
x(1 cos x3 cos x
x)
内蒙古工业大学
12
贾永旺
Advanced Mathematics
Advanced Mathematics
当
n
N
时恒有
1
yn a
,
当n
N
时恒有
2
zn
a
,
取 N max{N1 , N 2 }, 上两式同时成立,
即 a yn a , a zn a ,
当 n N时, 恒有 a yn xn zn a ,
即 xn a 成立,
lxim0 sinx
x
1
cos x2
x
1 cos
x
111 1 2
例5
求
lim
x 2
cos
2
x x
解 令t x 则当x 时t 0
2
2
于是 cos x
lim
x 2
2
x
cos( t)
lim 2
t0
t
lim sin t 1 t0 t
内蒙古工业大学
13
贾永旺
Advanced Mathematics
x x0 ( x )
那末 lim f ( x)存在, 且等于A. x x0 ( x)
A
A
A
(( 1
x0
内蒙古工业大学
y h( x) y f (x) y g(x)
x0
)) 2
x0
4
贾永旺
Advanced Mathematics 准则 Ⅰ和准则 Ⅰ'称为夹逼准则. 注意: (1).利用夹逼准则求极限关 键是构造出 yn与 zn ,
(2) lim(1 1 )x e
x
x
定义 lim(1 1)n e
n
n
设
xn
(1
1)n n
1 n 1 n(n 1) 1 n(n 1)(n n 1) 1
x0 2
x0
lim cos x 1, 又lim1 1,
x0
x0
lim sin x 1. x0 x
注 此结论可推广到 lim sin ( x) 1
xa ( x)
条件是x a时, ( x) 0,其中a可为
有限值,也可为
内蒙古工业大学
11
贾永旺
例3 解
求 lim x0
原式
1 coAs xdvanced Mathematics
sin x x tan x, 即 cos x sin x 1, x
上式对于 x 0也成立. 2
当 0 x 时,
2
内蒙古工业大学
10
贾永旺
Advanced Mathematics
0 cos x 1 1 cos x
2sin2 x 2
2( x )2
x2 ,
22
lim x 2 0, lim(1 cos x) 0,
如果数列 xn满足条件 x1 x2 xn xn1 , 单调增加 单调数列 x1 x2 xn xn1 , 单调减少
准则Ⅱ 单调有界数列必有极限. 几何解释:
x1 x2 x3xn xn1 A M
x
内蒙古工业大学
7
贾永旺
Advanced Mathematics
例2 证明数列 xn 3 3 3 (n重根 式)的极限存在.
1.夹逼准则
准则Ⅰ 如果数列xn , yn 及zn 满足下列条件: (1) yn xn zn (n 1,2,3)
(2)
lim
n
yn
a,
lim
n
zn
a,
那末数列 xn的极限存在,
且lim n
xn
a.
证 yn a, zn a,
0, N1 0, N2 0, 使得
内蒙古工业大学
2
贾永旺
证 显然 xn1 xn , xn是单调递增的 ;
又 x1 3 3, 假定 xk 3, xk1 3 xk 3 3 3,
xn是有界的 ;
lim n
xn
存在.
xn1
3 xn ,
x2 n1
3
xn ,
lim
n
x2 n1
lim(3
n
xn ),
A2 3 A, 解得 A 1 13 , A 1 13 (舍去)
函数 g(x), h(x) 之间,以便应用准则Ⅰ
内蒙古工业大学
9
贾永旺
Advanced Mathematics 作如图所示的单位圆
C B
设单位圆 O, 圆心角AOB x, (0 x )
2
作单位圆的切线,得ACO .
o
x
D
A
扇形OAB的圆心角为 x , OAB的高为 BD ,
于是有 sin x BD, x 弧 AB, tan x AC ,
