第12讲 等势面 电势梯度 静电场中的电偶极子
电势电势梯度

静电场的环路定理
当带电体在静电场中移动时,静电场力对带电体要作 功,这说明静电场具有能量。
一、静电场力的功
d A = F . d l = q E .dl b r rb = q E .dl cosφ dl qq φ φ q = q E .dr = 4 r 2d r π ε ra q E q q rb d r qq 1 1 a A= 2 = r r 4π 4 π ra r b ε a ε
§5-5
等势面 电场强度与电势梯度的关系
注:相邻等势面之间的电势差相等。
一.等势面:在静电场中,电势相等的点所组成的面。
等势面的性质: (2)等势面与电场线处处正交 (3)电场线指向电势降低的方向 (4)等势面和电场线密集 处场强量值大,稀疏处场强 量值小
(1)在静电场中,沿等势面移动电荷时,电场力作功为零
=
q 4πε
o
[
x (x + R )
2 2 3 2
]
V dV
B2
n
B3
dn φ
B1
dV E dn
V
dl
II I
E
dV E dn
负号表示E与n的方向相反,正是E的方向
dV E n gradV dn
电场中各点的场强等于各点的电势 梯度矢量的
负值。
任一方向的电场强度的分量:
V dV
B3 II dn φ
B2
n
1. 点电荷的电势 Vp =
p
E .dl =
8
q 4 πε 0 r
2
8
p
d r cos 0
0
q 1 1 4o r r a
等势面静电场中的电偶极子

2
2
qlE sin
M pE
pE sin
第9章 静电场
返回
17
南通大学
Nantong University
9-4 静电场中的电偶极子
当 p E 时, 90 M最大 M pE
当 p // E , 0 时, M=0
F
(C)
q
4 0 r R
(D)
q
4 0
1 R
1 r
P
R
q
r P'
[]
第9章 静电场
返回
22
南通大学
Nantong University
9-4 静电场中的电偶极子
3. 如图所示,在匀强电场 E 中取一半径为
R的半球面ACB,求:
(1)通过ACB半球面的电通量;
(2)沿 ACB 路径搬迁电荷q时,电场力所
返回
9
南通大学
Nantong University
9-4 静电场中的电偶极子
V V
V
en
A
B l
E
q 1
dV El dl
电场强度沿 l 方向 的分量,等于电势 沿这个方向空间变 化率的负值.
第9章 静电场
返回
10
南通大学
Nantong University
9-4 静电场中的电偶极子
南通大学
9-4 静电场中的电偶极子
Nantong University
例4:半径为R的无限长圆柱体,电荷按体密
度 分布,分别以(1)轴线处为零电势位
置,(2)圆柱体表面为零电势位置,求圆
电势场强微分关系,电偶极子,电介质

UP
k
p cos θ r2
k
p r r3
k
p
r0
r2
28
五、电介质(了解) 无极分子位移极化 有极分子取向极化 极化强度: 描述极化程度
P
pi
V
均匀电介质中的电场:E E0 r r 1 e 0r
29
r2
14
U
k
p r0
k
p cos
r2
r2
电势与p成正比, 与距离的平方成反比, 还与方位有关。
求中垂面上的电势:
U=kq/r+(-kq/r) = 0
U k p cos 0
r2
y
rr
q q l
x
15
A●
B
●
●C
U A 0;UB 0;UC 0
p cos
U k
r2
16
3 电偶极子电场中的场强
a q0E dl
3. 电势:(1)
UA
E dl
A
(2)
Ua
q
4 π 0r
4. 电势差:
b Ua Ub a E dl
2
6.3.1 场强与电势的关系
1 等势面(电势图示法) 等势面:电势相等的点连成的面。
规定任意两相邻等势面间的电势差相等
为什么这么规定?
3
等势面的特征:
➢电荷沿等势面移动时,静电力做功为零
电势沿法线n方向的变
化率: dU dU dn dl
电势沿法线n方向的变化最快
(电势变化率最大)
电势梯度:gradU
dU dn
n0
单位:V/m
9
3 电势与场强的微分关系
q0沿法线n方向从A移到B, 电场力做的功:
静电场的环路定理(北邮)

W Ua a q0
a
0
q 0 E dl
E
a
E dl
a
4、电势差:
U a U b E dl E dl
a b
E 减少, 能量哪里去了?
解: 由高斯定理
0
E
r RA r RB
2
q q
RA
q 4 0 r
RA r RB
RB
U AB U A U B
RB E dl
B A
q q 1 1 dr ( ) 2 40 RA RB RA 40 r
2.如图已知+q 、-q、R ①求单位正电荷沿adc 移至c ,电场力所作的功
例2:求半径为R、电量Q均匀分布的球面在 球心O处产生的电势。
dq Q dq 思路(1): dU U 4 0 R 40 R 40 R
好
(2):
U
O
E dl
R
O
E dl E dl
R
E dl R
F-
q
M
能量最低,稳定平衡。
, W pE 能量最大,非稳定平衡。
5、电场力作正功时,电势能减少,能量
哪里去了?
Aa b q0 E dl q0 ( U a U b )
b a
1 q0 ( Ua Ub ) mv 2 2
1eV=1.6×10-19J
求E 。
例:用电势梯度法计算带电圆环轴线上 一点的场强。 r
o x p X
04电势梯度、电偶极子-精选文档

5. 基本的电势分布 (1) 点电荷的电势
q Vp 4 0 r
(2) 均匀带电球面的电势
Vin
u (r )
Q 4 0 R
Q Vout(r) 4 0r
0
R
r
(下一页)
§8 - 8 等势面 和电势梯度
一、 等势面 (1)等势面定义 :由电场中电势相等的点组成的曲面
c
即:等势面与电力线处处正交.
d
E
②电力线指向电势降低的方向; ★沿电力线移动 q d V W W q ( V V ) A E d l 0 ; c c d c d cd
c
V d
(下一页)
③等势面较密集的地方场强大,较稀疏的地方 场强小(证明待后)。
●
F
q
如果电偶极子放在非均匀电场中,所受合力不为零。则电 偶极子不仅要转动,而且还会作平动。 (下一页)
二、电偶极子在电场中的电势能和平衡位置
q ●
r0
●
F
电势分别为V 和V- 。 + E
Wp = qV+-qV-
r 如图 电偶极子 0 pq 在匀强电场 E 中。 设 q 和 q 所在处的
等势面类比于地形图中的等高线.
(2)等势面的获得:
①利用电势的解析表达式:
V ( x , y , z ) V , i 1 , 2 , 3 ... i
②利用实际测量的方法.
规定:场中任意两相邻等势面间的电势差相等
+
(3)等势面的例子
正点电荷电场 中的等势面 (下一页)
电偶极子的等势面
+
(下一页)
【大学物理】静电场的环路定理 电势 等势面 电势梯度
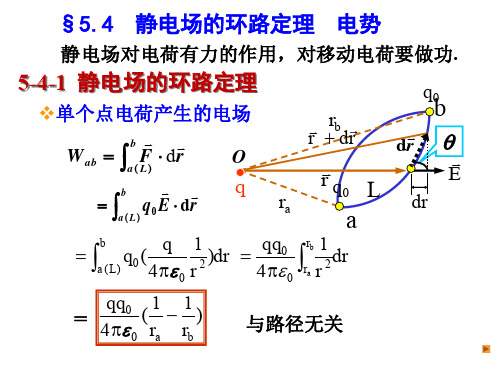
r r r r- r l cos
r
r
r+
q l
q+
3. 连续分布电荷电场中的电势 利用电势叠加原理:
dV
dq
dq VP 4 π 0 r
r
P
使用此公式的前提条件为有限大带电体且选无限远 处为电势零点;积分是对整个带电体的积分。 E 利用电势定义式: dl “ 0 ” P
qr E1 3 4 π 0 R
r
q E2 2 4 π 0 r
V1 E1dr E 2 dr
r R
R
q R
R
r
qr q dr dr 3 2 R 4 π r 4 π 0 R 0
2
q q q (3 R r ) 2 2 (R r ) 3 8 π 0 R 4 π 0 R 8 π 0 R
与路径无关
a
dr
任意带电体系产生的电场
任意带电体系都可以看成电荷系 q1、q2、…,移动q0, 静电力所作功为: b b q E •b dr W F dr 0
ab
q0 a• q0 ( E1 E 2 E n ) dr a( L) n b q 0 E i d r = qi q0 ( 1 1 ) a( L) i 1 rbi i 4 0 rai
注意:
• 电势能的零点可以任意选取,但是在习惯上, 当场源电荷为有限带电体时,通常把电势能的零 点选取在无穷远处。 这时,空间a点的电势能:
E pa
a
q0 E dl
• 电势能为电场和位于电场中的电荷这个系统所 共有。
物理 电磁学 第12讲 等势面 电势梯度 静电场中的电偶极子
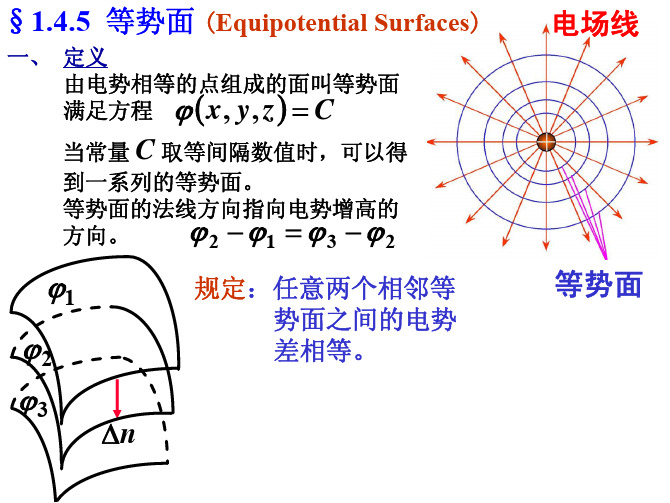
P3
e ˆr
P1
d
E dl Edlcos ( d ) d E cos E l l E x , E y , Ez y x z
E En n l max E e ˆn grad n
c
a A
C
0
等势面的疏密反映了场的强弱
设电场中任意两个相邻等势面之 间的电势差为一定的值
Δ
E P n Q
Δ Δ E Δn 或 E Δn
Δn 0
Δ E lim Δn 0 Δn
等势面密的地方场强大
1. 2. 两个基本定理
真空中静电场小结 两个物理量 E
[例] 求均匀带电圆盘 (R, ) 轴线上的场强。
2 0
R x x
2
2
O x P
x ˆ d ˆ i i 1 E 2 2 2 0 dx R x
Some hammerhead sharks can detect electric fields as weak as 50 picovolts per meter!
M p E
讨论: 当 p // E 时, W Wmin pE,M 0;稳定平衡态 当 p // E 时,W Wmax pE, M 0;非稳定平衡态
使电偶极子转向电场强度的方向。 (2) 非匀强电场
电偶极子不会平动 正、负电荷所受的对偶极子中心的力矩之和:
F F F qE qE 0
电偶极子会平动
M p E
一般而言,同时又会有转动,由于 l 很小,在计算力矩 时,可近似认为正、负电荷所在处的电场相同。 故电偶极子在非匀强电场中既有平动又有转动。
电势梯度、电偶极子课件

2 电偶极子的性质与特点
电偶极子具有矢量性质、具有二极性、具有 偶极矩和偶极矩矩量的概念。
3 电偶极子的电势与电场
电偶极子产生的电势与电场与距离的关系符 合特定的数学表达式。
4 电偶极子的应用与实例
电偶极子的应用广泛,涉及电子学、光学、 化学等多个领域。例如,它可以用于理解分 子极性、光电效应等。
示范演示文稿
电势梯度、电偶极子ppt 课件
本课件将详细介绍电势梯度以及电偶极子的相关知识。电势梯度是指在电场 中单位正电荷移动时电势能变化的快慢程度,与电场强度有密切关系。电偶 极子是指两个相等但异号的电荷之间的一对。通过本课件,您将深入了解电 势梯度与电偶极子的性质、计算方法以及应用实例。
电势梯度的定义
电势梯度
是指在电场中单位正电荷移 动时电势能变化的快慢程度。
电场强度与电势梯度的 关系
电场强度与电势梯度成正比, 即电场强度越大,电势梯度 越大。
电势梯度的计算方法
可以通过导数的定义来计算 电势梯度,即沿电场方向上 的导数。
电偶极子的定义
1 电偶极子
是指两个相等但异号的电荷之间的一对存在 特定距离关系的物理系统。
3 提问与答疑
如果您有任何与电势梯度和电偶极子相关的 问题,请随时提问。
4 结束语
感谢您的阅读,希望本课件能够对您在电学 学习中有所帮助。
总结
通过本课件,您已经了解了电势梯度与电偶极子在电ห้องสมุดไป่ตู้中的重要性。掌握电势梯度的计算方法和电偶极子的定 义、特性以及应用场景,将有助于更深入地理解电场的性质和电学原理。
1 重点回顾
电势梯度是单位正电荷移动时电势能变化的 快慢程度,与电场强度成正比。
2 讲解的要点
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第12讲等势面电势梯度
静电场中的电偶极子
电场线与等势面的关系
♉电场线处处垂直等势面
♉电场线指向电势降的方向
♉等势面的疏密反映了场的强弱
电场强度和电势的关系
积分关系式
⎰⋅=b a a l E
d ϕ0
=
b ϕ微分关系式
ϕ
ϕ-∇=-=g ra d E
k z j y i x ˆˆˆ∂∂+∂∂+∂∂=∇ϕ
ϕ
ϕ
ϕ
电偶极子( )在电场( )中所受的力矩 E
p M ⨯=电偶极子( )在均匀外场( )中的势能 E
p W ⋅-=E p E p 电场中的电偶极子
O 图中所示以 O 为心的各球冠
面为静电场的等势面,已知
ϕ1 < ϕ2 < ϕ3,在图上画出 a 、
b 两点的电场强度的方向,并
比较它们的大小。
E a E b
(填 <、=、>)。
ϕ1 ϕ2 ϕ3 a b = a E b E Q3.12.1
1.若静电场的某个区域电势等于恒量,则该区
域的电场强度分布是 ;若电势
随空间坐标作线性变化,则该区域的场强分布是 。
处处为零 不为零的恒量(或均匀分布) Q3.12.2
设有两个电偶极矩分别为 和 的电偶极子。
如果它们重叠在一起,此带电系统的电偶极矩为多少? 答:
1p 2p Q3.12.3
221121l q l q p p p
+=+=
Q3.12.4
电偶极子在均匀电场中总要使自身转向稳定平衡的位置,若此电偶极子处在非均匀电场中,它将怎样运动呢?你能说明吗?
答:见视频。
[Q3.12.5] 证明 Q1.3.7 中的电四极子在它的轴线延长线上的电势为
式中 Q = 2ql 2 叫做它的电四极矩。
利用梯度验证,所得场强公式与Q1.3.7一致。
)(l r r Q >>= π4130εϕ+q P
-2q +q l l r
解: 根据电势的叠加原理
⎪⎭⎫ ⎝⎛--++=r l r l r q 211π40εϕ+q P
-2q +q l l r
2π422220)
()()()(l r r l r l r r l r r q ---++-=ε)(22202π4l r r l q -=ε当 l << r 时, 3
0π4r Q
εϕ≈r E ∂∂-=ϕ40π43r Q ε=
[Q3.12.5]* 电偶极层: 一厚度 l 均匀的曲面薄壳,两面带
有符号相反的面电荷 。
e σ±求 P 点的电势和场强。
解:由电势叠加原理
⎰
-+⎰''='S S r
S
r S P d π41d π41e 0e 0)()(σεσεϕ⎰⎪⎭
⎫ ⎝⎛-'=)(S S r r d 11π40e εσ夹角
),(: ˆ n e r
θθ
cos l r r +≈'r
r
'
S
S 'e
σ-e σ+S
d S '
d n
ˆe θ
l
P
θcos 1
1l r r +≈'⎪
⎭⎫ ⎝
⎛+=r l r θcos 11⎪⎭⎫ ⎝⎛-≈r l r θcos 112
cos 1r l r θ-
=2cos 11r
l r r θ
-=-'⎰⎪⎭
⎫ ⎝⎛-'=)()(S S
r r P d 11π40e εσϕ⎰-=)(S S r l d cos π420e θεσ⎰
-=)
(S Ωl d π40e εσr
r ' S
S 'e σ-e σ+S d S 'd n ˆe θ
l
P
平面角
∙
O A B
θ
R
A '
B '
R
B A ''=θ(弧度)
S '
立体角 ∙
O
S
Ω
R
2R
S '
=Ω(球面度)
与 R 无关
Ω
S 'd 面元 S
d ∙
O S
d r
Ω
d 2d d r
S '=Ωn
ˆe r e
ˆθ2
cos d r
S θ=
⎰-=)
()(S Ω
l
P d π40e εσϕ定义电偶极层强度(层矩):
单位面积上的电偶极矩 l
e e στ≡Ω:曲面 S 对场点 P 所张的立体角
r
r ' S
S 'e σ-e σ+S d S 'd n ˆe θ
l
P
Ω
P 0
e
π4ετϕ-=)(Ω
- P - - - - Ω:曲面 S 对场点 P 所张的立体角
Ω
P 0
e
π4ετϕ-=)(+ 闭合曲面薄壳内: 0
e
ετϕ-
=)(P P '
闭合曲面薄壳外: 0
=')(P ϕ+ + + + + +
+
+ +
- - - - - 心肌细胞静息
讨论 (1) 电偶极层的电势和场强只与它对场点
所张的立体角这一几何性质有关。
Ω:曲面 S 对场点 P 所张的立体角
r
r ' S S
'e σ-e σ+S
d S '
d n ˆ
e θl P ΩP 0
e
π4ετϕ-=)(ΩP E ∇=-∇=0e π4ετϕ)(
(2) 几何上决定,电偶极层两侧
立体角有一 4p 的跃变。
负电荷一侧: ,
2
d cos d r
S Ωθ=
,,0cos 2π
><θθ0d >⎰=-S ΩΩ正电荷一侧: ,,0cos 2π
<>θθ0
d <⎰=+S
ΩΩr
r ' S
S 'e σ-e σ+S d S 'd n ˆe θ
l
P
具体考察图中两点
-
+ΩP ΩP −−−→−−−−→−-+立体角
立体角
π
4=+=-+-+-ΩΩΩΩ当该两点趋于偶极层表面时,相对应的立体角之差 电偶极层两侧的电势跃变
π4π40e ⨯=ετ)()(-+-P P ϕϕ)(-+--
=ΩΩ0e π4ετ0
e
ετ=。
