1储油罐的变位识别与罐容表标定_王力工指导
储油罐的变位标识与罐容表的标定

摘要为解决加油站的地下储油罐在使用一段时间后,由于地基的变形会导致无法根据预先标定的罐容表计算储油罐内油量容积的问题,研究如何识别储油罐变位以及对罐容表的重新标定的问题.得到储油罐的总油量与油标高度、纵向偏转角、横向偏转角之间的关系模型.利用该模型可根据加油站的出油量以及对应的油标高度来识别储油罐的变位,通过建立优化模型, 搜索算法和MATLAB软件求解出了所识别的变位的变位角度, 并利用实验数据对求解结果进行了检验; 最后利用得到的油量表达式给出了两个储油罐的罐容表.为了得到变位参数的有效估计,对进出油实测数据建立非线性的最小二乘回归模型,在数值求解中,采用截面积的微元方法,有效减少了复杂的体积积分计算,从而完成罐容表的修正标定。
关键词:MATLAB 变位标识罐容表标定储油罐ABSTRACTIn order to solve the problem that the calculation of oil tank volume must be calibrated periodically because an oil tank shift for the foundation deformation,the fuction relation between oil volume,altitude,direction deflection angle,transverse direction deflection angle is given out.The shift parameter Can be found with the model and data of oil volume.The new calculation of oil tank volume can be finned after tank shift.a1.Further more,we have gained the displacement angle by developing a optimization model, gradually decrease interval search algorithm and Matlab software, and then apply the experimental data to verify our solved results.We develop the non—linear of least squared regression model to estimate the parameters of position change.In particular,the differential element method of the sectional area is proposed to effectively reduce the complex numerical computation of integral.Therefore,the volume table is readjusted by the estimation of parameters of position change.Keywords:MATLAB;shift confirm ;calibration calculation of volume;oil tank第一章绪论1.1 储油罐问题的背景由来储油罐是储存油品的容器,在我们周边加油站是普遍存在的,一般加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,先通过流量计和油位计来测量进/出油量与罐内油位高度等数据,再通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,使地面上的人很容易了解罐内油位高度和储油量的变化情况。
储油罐的变位识别与罐容表标定

H 3 h' H 2 和 h' H 3 .
我们以第三种情况为例,来建立变位椭圆罐体模型. 首先,我们给出变位后的椭圆罐体纵向截面图,如下所示:
B
Q
P
h2 A
h1
M
l2
h
D
l1
N
图 3 椭圆罐体倾斜 角度时的横向截面图
在图 3 中, 我们以 D 点为端点作平行于 MN 的直线 DB ,B 点位于直线 AM 上. h1 表
y
b
O dx
a x
h
f(y)
图 2 小椭圆油罐体在无变位时的纵向截面图
图 2 中的 h 为小椭圆界面油量的高度,阴影部分就是罐体内部储油量的截面面积. 我们以椭圆圆心为圆点 O ,椭圆的长半轴为 x 轴,短半轴为 y 轴建立直角坐标系. 设椭 圆的长半轴为 a ,短半轴为 b ,根据这些变量我们可以容易得到椭圆的方程: x2 y 2 1 a 2 b2 由于截面面积的边界是和椭圆相连接的,不能够用 / 360 S 椭圆来求,所以我们 运用了数学上的积分来对此部分面积进行求解. 首先,我们先将面积分为左右两部分进行计算. 以右半部分为例,由于曲边梯形
4
度最高的 、 的值,并据此给出油位高度间隔 10 cm 的罐容表标定值,验证所建立的 模型的正确性与方法的可靠性.
五、模型的建立与求解
5.1 问题一模型的建立与求解 5.1.1 椭圆罐体模型的建立 在对问题一进行分析时, 我们分别对罐体无变位和纵向倾斜的变位情况进行了分析. 因此,我们针对这两种情况建立无变位椭圆罐体模型和变位椭圆罐体模型. 无变位椭圆罐体模型的建立 在椭圆罐体未发生纵向倾斜,即在无变位的情况下,油罐体与地面没有夹角,此时 0, 罐体内部的油量在液面各处都是平稳的. 下图为椭圆罐体在无变位时的纵向截面 图.
2010高教社杯全国大学生数学建模竞赛官方题目(含ABCD)
\A 题 储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β )之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm 的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
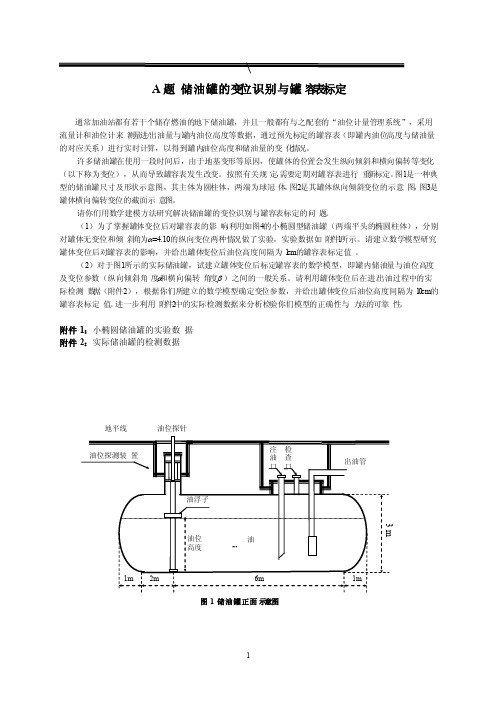
附件1:小椭圆储油罐的实验数据 附件2:实际储油罐的检测数据油油浮子出油管油位探测装置注油口 检查口地平线 2m6m1m1m3 m油位高度图1 储油罐正面示意图油位探针油位探针α地平线 图2 储油罐纵向倾斜变位后示意图油油浮子出油管油位探测装置注油口 检查口水平线(b) 小椭圆油罐截面示意图α油油浮子出油管油位探针注油口水平线2.05mcm 0.4m1.2m1.2m1.78m(a) 小椭圆油罐正面示意图图4 小椭圆型油罐形状及尺寸示意图图3 储油罐截面示意图(b )横向偏转倾斜后正截面图地平线β地平线垂直线油位探针(a )无偏转倾斜的正截面图油位探针油位探测装置地平线油3m油B题2010年上海世博会影响力的定量评估2010年上海世博会是首次在中国举办的世界博览会。
储油罐的变位识别与罐容表标定

储油罐的变位识别与罐容表标定摘要许多储油罐在使用一段时间后,由于地基变形等原因,使油罐发生纵向倾斜或者横向偏转,从而导致罐容表发生改变。
据此,我们用微积分与数据拟合的方法建立储油罐的变位识别与罐容表标定的模型。
通过对问题的分析,将问题化成若干个小问题,从而建立了五个数学模型。
其中模型一、二主要针对的是一问提出的,模型三、四、五针对的是二问提出的。
模型一通过用微积分知识确定了无变位时罐内油量与油位高度的关系式,并通过编写MATLAB程序对模型进行了求解。
模型二考虑变位时罐内油量与油位高度的关系,通过附件1中给的数据,拟合出了罐内油量的理论值与实验值之差v∆与油位高度h的关系式,通过v∆与h的关系式可以将倾斜角度α拟合进去,从而得到v∆与h、α的函数关系式,再根据v v v=-∆理实确定出v实的表达式。
模型三考虑的是无变位时储油量与油位高度的关系,与模型一不同的是储油罐的形状不同,通过二重积分求得储油量与油位高度的关系式,最后通过编写MATLAB程序对模型进行了求解。
模型四考虑的也是无变位时储油量与油位高度的关系,只是研究方法与模型三不同,即模型三和模型四是研究同一问题的不同方法。
模型四是将罐子看成一个卧式的圆柱体,求其体积,进而分析误差,并求出误差,最后也可得到较为精确的罐内油量与油位高度的关系式,最后通过编写MATLAB程序对模型进行了求解。
模型五考虑了横向和纵向的倾斜角度的变化,通过对附件2显示油高和显示油量容积两列数据的拟合确定油位高度为0时的罐内油量,即常数L,然后根据新建立的关系式和模型四来确定纵向倾斜角α和横向偏转角β,最终得到了存在倾斜角α和横向偏转角β罐内油量与油位高度的关系式。
应用以上五个模型可以很好的解决题中的两个问题,即模型一、二解决一问,模型三、四、五解决二问。
关键词:微积分数据拟合储油罐油位高度罐容表1 基本假设1)储油罐的形状是规则的2)油位高度为0时,罐内油量为常数L2 符号说明1) h ——油位高度2) l ——小椭圆形储油罐的长度3) a ——小椭圆形储油罐横截面椭圆的长半轴长 4) b ——小椭圆形储油罐横截面椭圆的短半轴长3 模型的建立、求解与应用3.1模型一3.1.1模型的建立对于(1)问,首先考虑储油罐无变位的情况,其横截面积如图:其阴影部分的面积2hs xdy =⎰ ,其中x =则 2v sl =理,其中v 理表示无变位罐内的油量。
2010年建模优秀论文解析

储油罐的变位识别与罐容表标定目录摘要本文对储油罐的变为识别和罐容表的标定问题进行了深入的探讨,针对这一问题,我们建立了数学模型,并利用matlab等软件对其进行求解。
针对问题一,我们利用了积分的方法推导出小椭圆储油罐在无变位和发生纵向倾斜变位时的储油量与油位高度之间的一般公式,然后把附表一中的变位前后油位高度分别代入两个模型求得体积,所求得的体积与附表一中相对应的累加进油量和罐内容量初始值之和基本相符,说明我们建立的模型是可以接受的。
用这两个模型变位前后的曲线,计算测量值与实际值之间的误差。
并利用变位后的模型给出间隔1cm的罐容表的标定值。
针对问题二,我们先考虑纵向倾斜,将实际模型分为三部分,分别求出左右球冠体,中间部分,的体积。
用Matlab求出高度H和体积V的一般关系。
再考虑横向倾斜,得到综合横向倾斜和纵向倾斜后H和V的关系。
根据附表2,用Matlab进行最小二乘,求解最小误差下纵向倾斜角α和横向倾斜角β。
得到油位高度间隔为10cm的罐容表标定值。
并通过附件2中实际数据,检验此模型可行性。
关键词:微元法;最小二乘法;Matlab;一问题重述通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
问题一:为了掌握罐体变位后对罐容表的影响,利用题中所给的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,并给出附件一。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm的罐容表标定值。
2010年我校参加全国大学生数学建模竞赛获全国二等奖论文A题

储油罐的变位识别与罐容表标定模型【摘要】本文针对油罐的变位识别和罐容表标定的具体问题,通过建立模型将储油分成无数个小微元,研究小微元的规律从而利用微积分的方法推导出,当纵向倾斜α角度和横向偏移β角度一定时,通过建立数学模型将储油罐中剩余油的体积与油位探针显示高度的函数关系表示出来,并制定罐容表标定值。
针对问题一:研究罐体变位对灌容表的影响,首先利用了逼近法计算油罐未变位前的储油体积,在MATLAB 中对实际与理论数据进行拟合利用误差分析公式真实值真实值理论值-=E ,求得其误差E 范围为034917.0E 014866.0≤≤,求储油罐中储油量时将油罐分成多部分考虑,利用微元思想和积分方法求得其储油量的体积与油位探针的读数h 及变位角α,β的函数关系()βα,,h f V =在此问中︒==1.4,0αβ时得出()0,1.4,︒=h f V ,求出其一定h 时的V 。
用模型求出的理论值与题目附表1中的实际值相比较,得出其误差%37.3%42.1≤≤E 。
并标出变位后间距为cm 1罐容表。
针对问题二:对实际储油罐建立罐体变位罐容表的标定模型。
在问题一的理论和方法的基础上加上球冠中的储油体积即可得到实际储油罐储油体积,并采用最小二乘法推导出所求变位参数α及β。
并得出当α及β一定时油位探针的高度与剩余储油体积的关系()h f V =,进而制定间距为cm 10罐容表标定值。
本文充分运用了数学分析、高等数学等知识对储油体积积分,并通过MATLAB 软件模拟的方法对理论数据进行了误差分析,以及运用最小二乘法估计其变位参数值α,β。
最后对模型的优缺点进行了评价,并给出了改进方向。
关键词:MATLAB 数据拟合、微元法、最小二乘法、罐容表标定1 问题重述A 题 储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
储油罐的变位识别与罐容表标定
2. 模型假设 2. 模型假设
2. 模型假设
1、假设当油面高度到达一定的高度后 、假设当油面高度到达一定的高度后 高度 不再出油。 不再出油。 2、由于压强关系,假设油面高度不 、由于压强关系, 能超过罐深的。 能超过罐深的。 3、因为考虑到储油罐横向偏移和纵向 、 倾斜的角度不会太大, 倾斜的角度不会太大,所以假设油罐 不会露出罐底。 不会露出罐底。
Y=0.0012x+74.6429
既而得出储油罐变位后的罐容表
4.模型建立与求解
油位高度 (cm) 8.5 9.5 10.5 11.5 储油量(L) 5.2948 14.9381 27.3736 42.0371 油位高度 (cm) 45.5 46.5 47.5 48.5 储油量(L) 1099.6 1139.3 1179.3 1219.5 油位高度 (cm) 82.5 83.5 84.5 85.5 储油量(L) 2647.3 2688.5 2729.4 2770.1
4.模型建立与求解
4.模型建立与求解
问题一
b O
图中椭圆弓形的高为 h,图中阴影部分为 , 储油横截面,先用定积分求储油体积。 储油横截面,先用定积分求储油体积。设弓形 的面积为 S ( h), 当 0 ≤ h ≤b 时
O
O
h (2b h ) a S ( h ) = ab arcsin + ( h b ) h (2b h ), b b
储油量(L)
油位高度(cm)
储油量(L)
油位高度(cm)
储油量(L)
48772.34 51269.78 53651.81 55896.23 57982.21 59881.01 61565.02 62982.81 64073.41 64664.82
储油罐的变位识别与罐容表标定
b b (2)当罐体变位时,设横截面椭圆方程为
x2 a2
(y
b)2 b2
1(a
b
0),
a=0.89,b=0.6,l=2.45. 由(9)式得 | x | a b2 (y b)2 . b 当油浮标的观测高度为 h 时,横截面面积
平面上的 n 个点(hi,Vi),i=1,2,…,n。需要寻找一个函数 f(x),使其在最小二乘 准则下与所有数据点最为接近。
设
f (x ) a0 a 1r 1x( )a r2 x2 ( ) amrm x ( ) ,
(1)
其中 rk (x) xk 是一组线性无关的函数, ak 是待定系数。 (k 1, 2, , m; m n)
A=(RTR)-1RTY. 4.2.2 体积的计算 (1)当罐体无变位时,设罐体横截面椭圆方程为
x2 a2
y2 b2
1(a
b 0),
(6)
其中 a=0.89,b=0.6.
解得| x | a b2 y2 a b2 (b h)2 .当油浮标的观测高度为 h 时,横截面
b
将(18)代入(11),得
S (z,h) 2 a (1.2h)(2.05z)tan b2 (y b)2 dy,
b0
(20)
将(20)代入(19)得罐体油量体积的表达式
1.2h2.05
V (h) ab l 2 tan dz
a (1.2h)(2.05z) tan
(2)S——只考虑纵向变位时,油面假想高度为 h 时,在罐体的 z 轴某点上平行 于罐底面圆作一横截面,所得油的横截面积,如图 5 所示。考虑罐体纵向变位时,
2010数学建模A题答案论文 储油罐的变位识别与罐容表标定
摘要
储油罐作为加油站常用的贮存设施,对油品在不同液面高度时的贮油量进行精确的 计量变得尤为重要,本文讨论了,加油站卧式储油罐的变位识别与罐容表标定问题。其 主要方法是参考卧式储油罐罐内油品体积标定测量技术,结合几何关系及积分计算,建 立储油罐内储油量,油位高度及变位参数(纵向倾斜角 与横向倾斜角 )之间的关系 模型。然后分析模型,在油位高度一定时,由储油量确定变位参数 与 的值,即为对 储油罐进行变位识别;在变位参数 与 一定时,根据油位高度可确定储油量,即为对 罐容表(罐内油位高度与储油量之间对应的函数关系表达式)进行标定。
地平线
油位探针
油位探测装置
注检 油查 口口
出油管
油浮子
3m
油位
油
高度
1m 2m
6m
1m
图 1 储油罐正面示意图
-2-
地平线 油位探测装置
油位探针
油浮子
注检 油查 口口
出油管
油
α
图 2 储油罐纵向倾斜变位后示意图
水平线
地平线
油位探针
油位探测装置
地平线 油位探针
油 油
β
3m
地平线垂直线
(a)无偏转倾斜的正截面图
-6-
S ' a2 / 2 (a h' )a sin( / 2)
公式(2)
从而求得所求截面面积: S ( a2 / 2 (a h')a sin( / 2)) cos
公式(3)
将式(3)带入式(1)求得: V ( a2 / 2 (a h' )a sin( / 2))l cos
首先,结合上述因素及汽油热膨胀系数,建立模型并对模型进行修正,修正热膨胀 所带来的计算误差。代入附表实际测量数据验证模型。
2010数学建模全国赛
储油罐的变位识别与罐容表标定摘要加油站储油罐受到地基等因素的影响会发生位置的变化,导致罐容表数据与事实不符,根据这个实际问题建立数学模型,利用二重积分求体积,通过对各种数据的分析,比如高度差,体积差,纵向倾斜角度,横向倾斜角度等,建立油位高度与储油量之间的对应关系(即罐容表)。
利用matlab ,spss 等数学软件对关系方程进行求解,绘制图表进行分析比较。
从实际情况出发,对无变位和已变位的罐体分别建立数学模型,用较为科学的方法减小了罐体变位对罐容表标定的影响。
优化了对罐容表的标定。
问题一研究两端平头椭圆柱罐体纵向变位对罐容表的影响。
首先,应用定积分中的微元法分别对无变位和已变位两种情况建立数学模型,即()h v d b h b b aH d 222--=和 ()h v d b h b baH d 22tan 4.02α+--=, 应用数学软件将函数图像与附件1所给实际数据呈现的图像进行比较,由附件1中的实际数据带入方程所得的数值与实际数值相比较,经计算误差较小,从而说明所建的模型具有一定合理性。
其次,通过对两种模型的对比进行识别,对两种情况下的罐内油位高度差的分析,识别罐体是否变位。
从已变位情况的数学模型分析知,给出已知纵向变位1.4=α时油位高度间隔为1cm 的罐容表标定值。
问题二研究实际储油罐在横纵向均有变位时罐内储油量与油位高度的变化关系。
建立了实际储油罐无变位数学模型,()2232235.182hh h d d h v --=通过对实际情况的分析,在油量一定的情况下,由储油量深度与变位参数α和β之间的关系分析可知,两种变位参数存在对应关系,而联系二者的就是油面到罐底的深度,对各项参数进行整合,研究油体体积、油位高度、变位参数之间的关系。
给出了三者之间的一种对应关系:()[]()[]()[]()[]22222tan 6cos 5.15.1tan 6cos 5.125.1tan 2cos 5.15.1tan 2cos 5.125.172αβαβαβαβ---+--++-----=h h h h d d h v用控制变量法分析出变位参数的对应关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
储油罐的变位识别与罐容表标定摘 要加油站都有地下储油罐,一般是通过查看罐容表得知储油罐的剩余油量。
由于地基变形等原因,储油罐会发生变位,从而导致罐容表的改变。
因此研究储油罐的变位识别与罐容表重新标定具有重要意义。
问题一,首先,把求平底椭圆柱储油罐的储油量的问题转化为求体积积分的问题,做三重积分时,利用了平行于椭圆柱母线的截面微元,并利用Maple 软件,求出储油量关于油位高度和倾斜角α的关系表达式;然后通过分析理论值和实验值的相对误差,利用0α= 的实验数据对该表达式进行了误差系数补偿,得到了储油量与罐内油位高度及倾斜角的关系的(,)V h α数学模型,利用 4.1α= 的实验数据对补偿后的模型进行了检验,平均相对误差由补偿前的5%变为不到2%;在分析变位后对罐容表的影响时取定不同油位高度,研究储油量关于倾斜角的变化关系,得到了当油位高度较高、较低及在一定中间范围时不同的变化规律。
然后基于此模型得到了变位后油位高度间隔为1cm 的罐容表标定值(见14、15页);问题二,研究了主体为圆柱、两端为球冠的储油罐变位后的罐容问题。
首先将该问题转化为球冠和圆柱所含油的体积积分问题。
圆柱所含油的体积可利用问题一中的模型求解(其中油位高度要经过一定转化);球冠部分利用三重积分直接运算很难计算;而后我们通过分析球冠采用了近似积分算法,得到了储油量关于显示油位高度、两个变为参数(横向偏转角及纵向倾斜角)的一般关系式;为求αβ、,基于此一般关系式(,,)V h αβ,建立了目标为理论出油量和实际出油量之差的平方和最小的优化模型,利用附表二中的出油量的前半部分数据,并利用逐步减小区间的搜索算法,αβ、同时逐次以10.01 、0.1、为步长,用Matlab 进行了三次搜索,求得 2.13, 4.44αβ== ;然后利用附表二中显示油高和显示储油量两组数据,与αβ、取为0 时显示油高对应的理论出油量进行比较,得到的相对误差的数量级为510-(见24页图);并利用附表二中出油量后半部分数据,与2.13, 4.44αβ== 时所得出的理论出油量进行比较,得到平均相对误差为0.57%,从而检验了模型的正确性与方法的可靠性。
最后利用此模型得到了变位后油位高度间隔为10cm 的储容表标定值(见23页)。
关键词:储油罐 油位高度 储油量 纵向倾斜角 横向偏转角一、问题重述通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β)之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm 的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
二.基本假设1、注油管、出油管及浮杆所占的体积忽略不计2、问题一中所给的是油桶内径的尺寸(即忽略壁厚对结果的影响)3、问题二中储油罐在没有变位时的罐容表准确无误4、假设在所研究的时间段内纵向倾斜角度α和横向偏转角度β保持不变三、符号说明四、问题的分析4.1概论该题主要是解决解决储油罐的变位识别与罐容表标定两个问题,而核心问题是求储油量关于显示油位高度、储油罐两个方向的转角的关系表达式。
求此表达式的思路是先求油所占的体积关于参量s(参量s为和油高相关的参量)及两角度的关系式,进而利用参量s和显示油高的关系式求得最终表达式;由于问题二中的圆筒具有旋转对称性(旋转时所要积分的体积形状不改变),故问题一和问题二中储油量关于和油高相关的参量s的表达式的求法(实际为三重积分)在本质上是一样的,而区别仅在于参量s和显示油高的的关系表达式。
4.2问题一对于问题一,可通过三重积分和Maple软件先求解储油量关于参量s和倾斜角的一般表达式,然后找到参量s和显示油高h的关系,代入表达式可得到储油量关于显示油高和倾斜角的表达式;然后将理论值与实验值对比,参阅资料得出误差修正方法,利用倾角为0 时的数据进行修正,并利用倾角为4.1 的数据对修正后的表达式进行检验,得到了较理想的模型。
然后基于此模型求出当倾斜角变化时对罐容表的影响,并得到4.1 时的罐容表标定值。
4.3问题二对于问题二,同问题一一样,也需找到储油量关于参量s和两方向倾角的一般表达式,由于积分过程很复杂,有必要对此积分进行近似求解,得到一般表达式后,再找到参量s和显示油高h的关系式,代入即可得到储油量关于参量s和两倾角αβ、的一般关系。
然后利用附表二中出油量和显示油高,基于一般关系式,确立优化目标为理论出油量和实验出油量的误差平方和最小,变量为两偏角的优化模型,利用逐步逼近的搜索算法,得到了两偏角的值。
变位后的罐容表很自然的可利用一般表达式得到。
最后利用附表二中的显示油高和显示油量(实际为无偏角时的油高关于油量的精确对应关系),对模型的准确性验证;利用实验出油量和理论出油量的对比,对模型的可靠性进行验证。
五、模型的建立与求解5.1问题一---两端平头的椭圆柱体5.1.1数据预处理根据附件1,在无变位的情况下,我们根据进油过程和出油过程分别作出储油量V随h变化的图,由上图可以看出,在无变位的情况下,用进油数据求得的()V h 进变化曲线几乎与用出油数据求得的()V h 出变化曲线相同。
此外,在有倾角的时候,同理作出下图。
图2有倾角进出油过程储油量与高度的关系对比同样可以得到上述结论。
这就意味着,进油过程和出油过程地位是相等的(基本是相同的),如果我们可以对所有的进油量和出油量求其对应的储油量V ,即可增加样本容量,减小误差。
因此,在后文的计算过程中,我们会将所有的进油量值和出油量值当做求储油量的样本点。
5.1.2倾斜角为(0)αα≠ 时计算储油量1V 的一般模型1)状态分析讨论先过哪个点:当(0)αα≠ 一定时,桶内油量不同,对应的储油量计算公式不同。
根据储油量的多少,可以将此问题分为5个状态。
如下图另一方面,不同的倾斜角所对应的5种状态有所不同,液面直线可能先过2O,或者先过4O点。
临界条件如下图所示:根据上图,我们可以求出此临界状态下的倾斜角1.2arctan26.12.45α=≈ ,即只要α小于这个角,当储油量增加时,液面直线必定先过2O点。
而在此题中,储油罐的倾角是由于地基变形等原因引起的,角度不可能太大。
在此问题中,我们认为,α不会大于临界值,即液面直线必定先过2O点。
因此,图4所表示的状态即为桶内油量的所有状态。
讨论先求那种状态:通过分析可知,在油罐倾斜的时候,如果运用积分的方法,不同的油位高度h ,储油量的求解公式也不同。
故求出的储油量1V 的公式应当为关于h 的分段函数。
2)储油量1V 的计算---油量特少和油量特多在油量特少的情况下,油面高度h 一直保持为零。
即无法通过h 的变化,求得储油量1V 。
即1V 在此情况下无法计算。
同理,对于油量特多的情况, 1V 无法计算。
3)储油量1V 的计算---油量较少根据已知条件,我们以O 点为坐标原点,建立空间直角坐标系,示意如下:图5油量较少立体示意图 在图5的基础上,我们设定相关参数,得下图图6油罐yoz 面截面图在上图中,截取在区间[,]z z dz 内的体积元dV 。
然后将dV 在xoz 面的截面图,如下:图7油罐xoz 面的截面图参考图5后,体积元dV 为长方体。
若以xoy 面为底面,其面积为S '底,根据图6中的各个参数,可以求得此矩形底面的长和宽。
长:在图6中,有如下等量关系:tan hAC α=(1) tan hOC c α=+(2)tan tan OD OC h c αα==+ (3) 据几何关系得, tan DE OD OE h c z α=-=+-(4)tan tan tan DE h c zEF ααα+-===长 (5)宽:2P Q ''==宽 (6)底面面积:2S '=底(7)体积元体积:2dV S dz '==底面 (8)积分区间:求储油量须从O 到D 点对z 积分,积分区间为[0,]OD ,其中由(9)式得tan OD h c α=+。
积分模型:储油量1()V h 满足tan tan 110()2h c h c V V h dV αα++===⎰⎰(9)化简结果:用Maple 求解(15)式,化简后得到22213()(2a r c s i n 2)2()6t a n a b s V b b s s b b s b b πα-⎧⎫⎤=----+-⎨⎬⎦⎩⎭(10) 其中,(,)tan s s h OD h c αα===+。
由已知条件得0.89a =,0.6b =,0.4c =。
因此(10)式中,s 只是间接变量,最终唯有h 是自变量,即1111()[(,)](,)V V s V s h V h αα=== (11)4)储油量1V 的计算---油量中等参考图3,延长液面直线,得到油量中等状态的示意图如下:图8油量中等状态示意图由图中几何关系可得11(,)tan s s h h c αα==+(12)22(,)tan s s h h d αα==- (13)根据上图,并联系(16)、(17)式,得到此情况下储油量满足11112()()V V s V s =- (14)解(20)式得此情况下储油量为11122122112222212(,)[(,),(,)]{3[()2()arcsin 2()arcsin ]6tan ()]()]}V h V s h s h a b s b s b s s b s b s b b b b s b b s αααπα=--=----+--+-++- (15)5)储油量1V 的计算---油量较多图9油量较多状态示意图由图中几何关系求得33(,)2tan s s h b h d αα==-- (16) 根据圆柱体积公式得V S L abL π==椭油罐 (17)故可以利用公式(16)、(17),求得此情况下的储油量113233223(,)[(,)]{3()(2arcsin )6tan 2()}V h V V s h a b s abL b b s b b b b s ααππα=--=+--⎤-+-⎦油罐(18)6)问题一误差修正前模型参考图3,由几何关系易得各条临界线所对应的油位高度h :1234:0:tan :2()tan :2l h l h d l h b d L l h b αα=⎧⎪=⎨=+-⎪=⎩(19)综上,倾斜角为 4.1α= 时储油量1V 可以分段表示为: ①当h 一直保持0时,1V 无法计算; ②当0tan h d α<≤时,22211(,)[(,)]3()(2arcsin )2()6tan a b s V h V s h b b s b b s b b ααπα-⎧⎫⎤==----+-⎨⎬⎦⎩⎭其中,(,)tan s s h OD h c αα===+ ③当tan 2()tan d h b d L αα<≤+-时,11122122112222212(,)[(,),(,)]{3[()2()arcsin 2()arcsin ]6tan ()]()]}V h V s h s h a b s b s b s s b s b s b b b b s b b s αααπα=--=----+--+-++-其中,11(,)tan s s h h c αα==+,22(,)tan s s h h d αα==- ④当2()tan 2b d L h b α+-<≤时,2313223(,){3()(2arcsin)6tan2()}a b sV h abL b b sb bb b sαππα-=+--⎤-+-⎦其中33(,)2tans s h b h dαα==--⑤当h一直保持0是,1V无法计算5.1.3倾斜角为0α= 时计算储油量V的模型由于在1(,)V hα的分段表达式,总会存在tanα出现在分母上,故0α= ,即无变位的储油量需要单独计算依据题意,在已知参数a、b、、L的前提下,根据微积分的思想,在xoy面[,]z z dz+截取一个体积元dV,厚度为dz。
