圆的垂径定理练习题
垂径定理实例练习题

垂径定理实例练习题
根据垂径定理,设有一个圆,有一个直径和一个点位于该圆上,连接该点与直径的两个端点,则连接该点与圆心的线段垂直于直径。
下面是一些关于垂径定理的实例练题:
1. 问题描述:在一个圆上,有一条直径AB,并且连接圆上一
点C与直径的两个端点A和B,证明线段AC与线段BC互相垂直。
解答:因为AC连接了圆上的一点与圆心,所以根据垂径定理,线段AC与直径AB垂直。
同理,线段BC与直径AB也垂直。
因此,线段AC与线段BC互相垂直,证毕。
2. 问题描述:在圆P上,有一条直径EF,并且连接了圆上一
点D与直径的两个端点E和F。
已知EF长度为10厘米,点D离
圆心的距离为8厘米,求线段DF的长度。
解答:根据垂径定理,因为点D连接了圆上的一点与圆心,所以线段DF垂直于直径EF。
由于EF长度为10厘米,根据直角三角
形的性质,可以使用毕达哥拉斯定理计算线段DF的长度。
根据毕达哥拉斯定理,我们有:
其中,c代表斜边(即线段EF),a和b代表直角边(即线段DF和DE)。
已知EF长度为10厘米,代入公式可得:
解方程可得DF的值为6厘米,即线段DF的长度为6厘米。
以上是垂径定理的一些实例练习题的讲解。
希望能够帮助你理解和应用垂径定理。
如有任何问题,请随时向我提问。
专题2.1 圆中垂径定理综合应用(3大类题型)(原卷版)
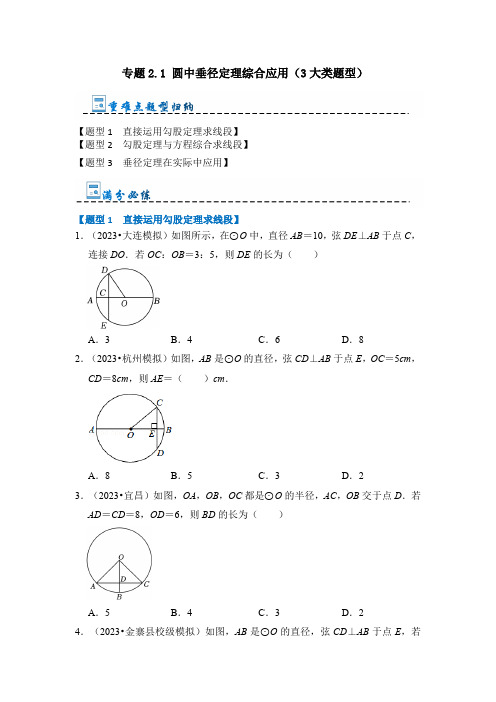
专题2.1 圆中垂径定理综合应用(3大类题型)【题型1 直接运用勾股定理求线段】【题型2 勾股定理与方程综合求线段】【题型3 垂径定理在实际中应用】【题型1 直接运用勾股定理求线段】1.(2023•大连模拟)如图所示,在⊙O中,直径AB=10,弦DE⊥AB于点C,连接DO.若OC:OB=3:5,则DE的长为()A.3B.4C.6D.8 2.(2023•杭州模拟)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=()cm.A.8B.5C.3D.2 3.(2023•宜昌)如图,OA,OB,OC都是⊙O的半径,AC,OB交于点D.若AD=CD=8,OD=6,则BD的长为()A.5B.4C.3D.2 4.(2023•金寨县校级模拟)如图,AB是⊙O的直径,弦CD⊥AB于点E,若CD=6,AB=10,则AE的长为()A.1B.2C.3D.4 5.(2023•亳州三模)如图,在⊙O中,直径AB⊥CD于点H.若AB=10,CD =8,则BH的长为()A.5B.4C.3D.2 6.(2023•容县一模)如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为点E,CD=8cm,AB=10cm,则AE=.7.(2023•衡南县三模)在⊙O中,直径AB=4,弦CD⊥AB于P,OP=,则弦CD的长为.8.(2023•东台市校级模拟)如图,A、B、C是⊙O上的点,OC⊥AB,垂足为点D,若OA=5,AB=8,则线段CD的长为=.9.(2023•望城区模拟)如图,AB是⊙O的直径,且AB=10cm,弦CD⊥AB 于点E,CD=8cm,连接OC,则BE=cm.10.(2023•长沙县二模)如图,⊙O的半径为5,弦AB=8,点C是AB的中点,连接OC,则OC的长为.【题型2 勾股定理与方程综合求线段】11.(2023•邯郸模拟)如图,以CD为直径的⊙O中,弦AB⊥CD于M.AB=16,CM=16.则MD的长为()A.4B.6C.8D.10 12.(2022秋•南开区校级期末)如图,在⊙O中,半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC,若AB=8,CD=2,则EC的长度为()A.B.8C.D.13.(2022秋•文登区期末)如图,AB为⊙O的直径,弦CD⊥AB于点E,若AE=CD=8,则⊙O的半径为()A.3B.4C.D.5 14.(2022秋•西湖区校级期末)如图,AB是⊙O的直径,弦CD⊥AB交于点E.若BE=10,CD=8,则⊙O的半径为()A.3B.4.2C.5.8D.6 15.(2022秋•泰山区校级期末)一块圆形宣传标志牌简图如图所示,点A,B,C在⊙O上,CD垂直平分AB于点D.现测得AB=16dm,DC=4dm,则圆形标志牌的半径为()A.6dm B.5dm C.10dm D.3dm 16.(2022秋•任城区校级期末)如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=2寸,AB=16寸,直径CD的长是()A.28寸B.30寸C.36寸D.34寸17.(2023•汉阳区校级一模)如图,CD为⊙O直径,弦AB⊥CD于点E,CE =1,AB=6,则CD长为()A.10B.9C.8D.5 18.(2023•汇川区三模)在半径为r的圆中,弦BC垂直平分OA,若BC=6,则r的值是()A.B.C.D.19.(2023春•仪征市期末)如图,AB是⊙O的直径,弦CD⊥AB于点E,,BE=1,则OC=.20.(2023•大冶市一模)如图,AB是⊙O的弦,C是AB的中点,连接OC并延长交⊙O于点D.若CD=1,AB=4,则⊙O的半径是.【题型3 垂径定理在实际中应用】21.(2022秋•海淀区校级月考)如图,一条公路的转弯处是一段圆弧AB,点O 是弧AB的圆心,C为弧AB上一点,OC⊥AB,垂足为D.已知AB=60m,CD=10m,求这段弯路的半径.22.(2022秋•郾城区期中)如图是一根圆形下水管道的横截面,管内有少量的污水,此时的水面宽AB为0.6米,污水的最大深度为0.1米.(1)求此下水管横截面的半径;(2)随着污水量的增加,水位又被抬升0.7米,求此时水面的宽度增加了多少?23.(2022秋•沭阳县期中)如图是某蔬菜基地搭建一座圆弧型蔬菜棚,跨度AB=3.2米,拱高CD=0.8米(C为AB的中点,D为弧AB的中点).(1)求该圆弧所在圆的半径;(2)在距蔬菜棚的一端0.4米处竖立支撑杆EF,求支撑杆EF的高度.24.如图,有一拱桥是圆弧形,它的跨度(所对弦长)为60m,拱高18m,当水面涨至其跨度只有30m时,就要采取紧急措施.某次洪水来到时,拱顶离水面只有4m,问是否需要采取紧急措施?25.如图,残缺轮片上弦AB的垂直平分线交弧AB于点C,交弦AB于点D,已知AB=24cm,CD=8cm.(1)找出此残缺轮片所在圆的圆心(写出找到圆心的方法);(2)求此圆的半径.26.某地有一座圆弧形拱桥,所在圆的圆心为点O,桥下水面宽度AB为7.2m,过点O作OC⊥AB于点D,交圆弧于点C,CD=2.4m(如图).现有一艘宽3m、船舱顶部高出水面AB2m的货船要经过这座拱桥,此货船能否顺利通过这座拱桥?27.我国古算书《九章算术》中有“圆材埋壁”一题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径(直径)几何?”(注:如图,⊙O表示圆材截面,CE是⊙O的直径,AB表示“锯道”,CD表示“锯深”,1尺=10寸,求圆材的直径长就是求CE的长.)28.如图,半圆拱桥的圆心为O,圆的半径为5m,一只8m宽的船装载一集装箱,箱顶宽6m,离水面AB高3.8m,这条船能过桥洞吗?请说明理由.29.(2022秋•沭阳县校级月考)如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且AB=26m,OE⊥CD于点E.水位正常时测得OE:CD=5:24(1)求CD的长;(2)现汛期来临,水面要以每小时4m的速度上升,则经过多长时间桥洞会刚刚被灌满?30.(2022秋•东台市期中)如图,是一张盾构隧道断面结构图.隧道内部为以O为圆心,AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为1.6m,顶棚到路面的距离是6.4m,点B到路面的距离为4.0m.请求出路面CD的宽度.(精确到0.1m)。
垂径定理练习题及答案

垂径定理练习题及答案一、选择题1. 在一个圆中,如果一条直径的端点与圆上一点相连,这条线段的中点与圆心的距离是直径的()A. 一半B. 半径B. 直径D. 无法确定2. 垂径定理指出,如果一条线段是圆的直径,那么它与圆上任意一点连线所形成的直角三角形的斜边是()A. 直径B. 半径C. 线段D. 无法确定3. 圆内接四边形的对角线互相平分,且其中一条对角线是圆的直径,那么这个四边形是()A. 平行四边形B. 矩形C. 菱形D. 无法确定4. 如果圆的半径为r,那么圆的直径是()A. 2rB. rC. r的平方D. 2r的平方二、填空题1. 垂径定理告诉我们,如果一条线段是圆的直径,那么它与圆上任意一点连线所形成的直角三角形的斜边是______。
2. 圆的内接四边形中,如果对角线互相平分,且其中一条对角线是圆的直径,那么这个四边形的对角线长度相等,等于______。
3. 已知圆的半径为5cm,那么圆的直径是______。
三、解答题1. 已知一个圆的半径为7cm,圆内有一点P,连接点P和圆心O,得到线段OP。
如果OP的长度为4cm,求点P到圆上任意一点的距离。
2. 一个圆的直径为14cm,圆内接四边形ABCD,其中AC为直径。
已知AB=6cm,求BC的长度。
四、证明题1. 证明:如果一个三角形是直角三角形,且斜边是圆的直径,那么这个三角形的外接圆的直径是这个三角形的斜边。
2. 证明:如果一个圆的内接四边形的对角线互相平分,且其中一条对角线是圆的直径,那么这个四边形的对角线长度相等。
答案:一、选择题1. A2. A3. B4. A二、填空题1. 直径的一半2. 圆的直径3. 10cm三、解答题1. 点P到圆上任意一点的距离是3cm(利用勾股定理,OP为直角三角形的一条直角边,半径为斜边,另一直角边为点P到圆上任意一点的距离)。
2. BC的长度是8cm(利用圆内接四边形的性质,对角线互相平分,且AC是直径,所以BD=7cm,再利用勾股定理求BC)。
垂径定理练习题4套

1、已知:AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为_______。
2、在⊙O中,P为其内一点,过点P的最长的弦为8cm,最短的弦长为4cm,则OP =____ _。
3、已知圆的半径为5cm,一弦长为8cm,则该弦的中点到弦所对的弧的中点的距离为__ _____。
4、已知圆心到圆的两条平行弦的距离分别是2和3,则两条平行弦之间的距离为_ ____。
5、在半径为5cm的圆内有两条互相平行的弦,一条弦长为8cm,另一条弦长为6cm,则这两条弦之间的距离为_____ _。
6、如图,在⊙O中,OA是半径,弦AB=cm,D是弧AB的中点,OD交AB于点C,若∠OAB=300,则⊙O的半径____cm。
7、在⊙O中,半径OA=10cm,AB是弦,C是AB弦的中点,且OC:AC=3:4,则AB=_____。
8、在弓形ABC中,弦AB=24,高CD=6,则弓形所在圆的半径等于。
9.如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点,AB=10cm,CD=6cm,则AC的长为_____。
1、已知:AB 是⊙O 的直径,弦CD ⊥AB 于点P ,CD =10cm ,AP:PB =1:5,则⊙O 的半径为_______。
2、在⊙O 中,P 为其内一点,过点P 的最长的弦为8cm ,最短的弦长为4cm ,则OP =____ _。
3、已知圆的半径为5cm ,一弦长为8cm ,则该弦的中点到弦所对的弧的中点的距离为__ _____。
4、已知圆心到圆的两条平行弦的距离分别是2和3,则两条平行弦之间的距离为_ ____。
5、在半径为5cm 的圆内有两条互相平行的弦,一条弦长为8cm ,另一条弦长为6cm ,则这两条弦之间的距离为_____ _。
6、如图,在⊙O 中,OA 是半径,弦AB =310cm ,D 是弧AB 的中点,OD 交AB 于点C ,若∠OAB =300,则⊙O 的半径____cm 。
《垂径定理-弧弦圆心角-圆周角》练习

1《圆》练习题(垂径定理, 弧、弦、圆心角, 圆周角)一、选择题1.已知在⊙O 中, 弦AB 的长为8厘米, 圆心O 到AB 的距离为3厘米, 则⊙O 的半径是( )A. 3厘米B. 4厘米C. 5厘米D. 8厘米2.半径等于12的圆中, 垂直平分半径的弦长为( )A. B. C. D.3.如图1, 在⊙O 中, ∠ABC=50°, 则∠AOC 等于( )A. 50°B. 80°C. 90°D. 100°4.如图2, AB 是⊙O 的直径, ∠ABC=30°, 则∠BAC =( )A. 90°B. 60°C. 45°D. 30°5.如图3, △ABC 内接于⊙O, 连结OA.OB, 若∠ABO =25°, 则∠C 的度数为( ).A. 55°B. 60°C. 65°D. 70°6.如图4, 四边形ABCD 内接于⊙O, 若它的一个外角∠DCE=70°, 则∠BOD=( )A. 35°B.70°C. 110°D.140°7、如图5, △ABC 内接于⊙O, AD ⊥BC 于点D, AD=2cm, AB=4cm, AC=3cm, 则⊙O 的直径是( )A. 2cmB. 4cmC. 6cmD. 8cm8、如图6, BD 是⊙O 的直径, 圆周角∠A = 30(, 则∠CBD 的度数是( )A. 30(B. 45(C. 60(D. 80(9、如图7, AB 为⊙O 的直径, C .D 是⊙O 上的两点, ∠BAC=30º, AD=CD, 则∠DAC 的度数是( )A. 30ºB. 60ºC. 45ºD. 75º10、圆内接四边形ABCD 中, ∠A ∶∠B ∶∠C ∶∠D 可以是( )A. 1∶2∶3∶4B. 1∶3∶2∶4C. 4∶2∶3∶1D. 4∶2∶1∶3AB O C图1 图2 O 30D B C A O D CBA 图3 图4图6图7图52二、填空题11.如图8, ∠A 是⊙O 的圆周角, ∠A=40°, 则∠OBC 的度数为_______.12.如图9, AB 是⊙O 的直径, 点D 在⊙O 上∠AOD=130°, BC ∥OD 交⊙O 于C, 则∠A= .13、如图10, ⊙O 的直径AB=8cm, C 为⊙O 上的一点, ∠BAC=300, 则BC= .14、如图,量角器外沿上有A 、B 两点,它们的读数分别是70°、40°,则∠1的度数为 .三、解答题: 15、.如图, AB 、CD 是⊙O 的两条弦, 延长AB 、CD 交于点P, 连结AD 、BC 交于点E . , , 求 的度数.16.如图所示, AB 是⊙O 的一条弦, OD ⊥AB , 垂足为C, 交⊙O 于点D , 点E 在⊙O 上。
圆的垂径定理习题及答案

圆的垂径定理习题一. 选择题 1.如图1,00的直径为10,圆心0到弦AB 的距离0M 的长为3,那么弦AB 的长是( )2.如图,O 0的半径为5,弦AB 的长为8,M 是弦AB 上的一个动点,则线段0M 长的最小值为()3.过O 0内一点M 的最长弦为10cm 最短弦长为8cm 则0M 的长为()A* 9cmE, 5cm4.如图,小明同学设计了一个测量圆直径的工具,标有刻度的尺子 0A 0B 在 0点钉在一起,并使它们保持垂直,在测直径时,把 0点靠在圆周上,读得刻度0E=8个单位,0F=6个单位,则圆的直位 D. 15个单位5.如图,00的直径AB 垂直弦CD 于 P,且P 是半径0B 的中点,6cmCD ,则直径AB 的长是()6. 下列命题中,正确的是(A .平分一条直径的弦必垂直于这条直径B .平分一条弧的直线垂直于这条弧所对的弦C .弦的垂线必经过这条弦所在圆的圆心D .在一个圆内平分一条弧和它所对的弦的直线必经过这个圆的圆心7. 如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为A.4B. 6C. 7D. 8 B. 3 C. 4 D. 5B . 10个单位 C. 1个单A . 212个单位E & 5米B, 8米C. 7米D,出米D8.0O 的半径为5cm 弦AB//CD ,且AB=8cm,CD=6cn 则AB 与CD 之间的距离为( ) A . 1 cm B. 7cm C. 3 cm 或 4 cm D. 1cm 或 7cm9•已知等腰△ ABC 的三个顶点都在半径为5的0 0上,如果底边BC 的长为8,那么BC 边上的高为 ( ) A . 2 B. 8 C. 2 或 8 D. 3 二、填空题1. _________________________________________________________________________ 已知AB 是O 0的弦,AB= 8cm, OCL AB 与C, 0C=3cm 则O 0的半径为 __________________________ c m2. ____________________________________________________________________ 在直径为10cm 的圆中,弦 AB 的长为8cm,则它的弦心距为 _______________________________ cm3. 在半径为10的圆中有一条长为16的弦,那么这条弦的弦心距等于 _____________________4. 已知AB 是O 0的弦,AB= 8cm, OC L AB 与C, 0C=3cm 则O O 的半径为 ________________ cm5. ______________________________________________________________________________ 如图,O 0的直径AB 垂直于弦CD ,垂足为E ,若/C0氐120°, 0E= 3厘米,贝U CD= ___________ 厘6. _____________________________________________________________ 半径为6cm 的圆中,垂直平分半径 0A 的弦长为 _______________________________________________ c m7. 过O 0内一点M 的最长的弦长为6cm,最短的弦长为4cm,则0M 勺长等于 cm8. 已知AB 是O 0的直径,弦CDL AB E为垂足,CD=8 0E=1则AB= __________9. 如图,AB 为O 0的弦,O 0的半径为5, OC L AB 于点D,交O 0于点C,且CD= l ,则弦AB 的长11. __________________________ 如图,在直角坐标系中,以点P 为圆心的圆弧与轴交于 A 、B 两点,已知P(4, 2)和A(2, 0), 贝卩点B 的坐标是12. ____________________________________________________________ 如图,AB 是O 0的直径,ODL AC 于点D, BC=6cm 则0D ________________________________ cm10. 某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知 AB= 16m 半径04 10m 则中间柱 CD的高度为13. 如图,矩形ABCDf圆心在AB上的圆0交于点G B、F、E, GB=10 EF=8 那么AD= ______14.___________________________________________________________________________ 如图,O O 的半径是 5cm P 是o o 外一点,PO=8cm / P=3GO,则 AB ______________________ cm是 __________________ Cm16. 已知AB 是圆O 的弦,半径OC 垂直AB 交AB 于D,若AB=8 CD=2则圆的半径为 _______________ 17. 一个圆弧形门拱的拱高为1米,跨度为4米,那么这个门拱的半径为 ___________________ 米 18. 在直径为10厘米的圆中,两条分别为6厘米和8厘米的平行弦之间的距离是厘米19. 如图,是一个隧道的截面,如果路面AB 宽为8米,净高CD 为8米,那么这个 隧道所在圆的20. 如图,AB 为半圆直径,O 为圆心,C 为半圆上一点,E 是弧AC 的中点,OE 交弦AC 于点0 若 AC=8cm DE=2cm 则 OD 的长为 _____________ c m21. 已知等腰△ ABC 的三个顶点都在半径为5的。
初中垂径定理试题及答案

初中垂径定理试题及答案一、选择题1. 在圆中,垂直于弦的直径是该弦的()。
A. 垂线B. 垂径C. 弦心距D. 弦长答案:B2. 垂径定理告诉我们,如果一条线段垂直于弦,并且平分弦,那么它也平分弦所对的()。
A. 弧B. 圆心角C. 弦心距D. 弦长答案:A3. 在圆中,如果一条直径垂直于弦,那么这条直径将弦分成的两段长度()。
A. 相等B. 不相等C. 无法确定D. 取决于圆的大小答案:A二、填空题4. 在圆中,如果弦AB的中点为M,且直径CD垂直于弦AB于点M,则弦AB所对的弧ACB的度数为______。
答案:90°5. 垂径定理在圆的几何学中非常重要,它说明了垂直于弦的直径将弦平分,并且平分的弦所对的弧是______。
答案:相等的三、解答题6. 已知圆O的半径为10cm,弦AB垂直于直径CD于点M,求弦AB的长度。
答案:由于直径CD垂直于弦AB,根据垂径定理,弦AB被直径CD平分,因此弦AB的长度为圆的直径,即20cm。
7. 在一个圆中,弦AC的长度为12cm,弦BC的长度为8cm,且AC和BC相交于点O,求圆的半径。
答案:由于AC和BC相交于圆心O,根据垂径定理,OA=OC,OB=OA,因此OA=OC=6cm,OB=OA=6cm。
根据勾股定理,圆的半径r满足r^2 =OA^2 + OB^2 = 6^2 + 6^2 = 72,所以r = √72 = 6√2 cm。
四、证明题8. 证明:在圆中,如果一条直径垂直于弦,那么这条直径将弦平分。
答案:设圆心为O,直径为CD,弦为AB,且CD垂直于AB于点M。
要证明CM=MD。
由于CD是直径,所以∠CMO=∠DMO=90°。
根据垂径定理,CM=MD,因此这条直径将弦平分。
圆垂径定理综合应用六十道经典题(答案解析)

(1)这条公路上的车辆形成的噪音是否会对学校造成影响?
(2)若车辆形成的噪音会对学校造成影响,为消除噪音,计划在公路边修筑一段消音墙,请你计算消音墙的长度.(只考虑声音的直线传播)
37.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC、BC,若∠BAC=30º,CD=6cm.
(1)求∠BCD的度数;
(2)求⊙O的直径.
38.如图,AC为⊙O的直径,CD为⊙O的弦,BE⊥CD于点E, = .
(1)求证:BE的⊙O切线.Fra bibliotek(2)若AD=4,EC=1,求BD的长.
39.如图,A,B,C是⊙O上的点,其中 ,过点B画BD⊥OC于点D.
C.若△BCD是等腰三角形,则△ACD也是等腰三角形
D.若PB=4PA,则CD=PB
3.如图,在 中, , 为互相垂直且相等的两条弦, , ,垂足分别为 , ,若 ,则 的半径是()
A. B. C. D.
4.如图, 的直径为10,弦 , 是 上一个动点,则 的最小值为()
A.2B.3C.4D.5
5.如图是一个圆弧形门拱,拱高 ,跨度 ,那么这个门拱的半径为()
A. B. C. D.
11.平面直角坐标系中,在以(2,1)为圆心,5为半径的圆上的点的坐标是()
A.(4,7)B.(-1,-2)C.(5,4)D.(2,-4)
12.如图,⊙O的半径OA=8,以A为圆心,OA为半径的弧交⊙O于B,C点,则BC=( )
A. B. C. D.
13.如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,AC=4,则OD的长为( )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆的垂径定理练习题
圆的垂径定理是几何学中的重要定理之一,它给出了圆上的垂径之间的关系。
在这篇文章中,我们将通过一些练习题来加深对这个定理的理解和应用。
练习题一:给定一个半径为5的圆,其中一条垂径的长度为12。
求另一条垂径的长度。
解析:根据圆的垂径定理,垂径的乘积等于半径的平方。
设另一条垂径的长度为x,则有12 * x = 5 * 5。
解这个方程可以得到x的值,进而求出另一条垂径的长度。
练习题二:在一个半径为8的圆中,一条垂径的长度为15。
求另一条垂径的长度。
解析:同样地,根据圆的垂径定理,垂径的乘积等于半径的平方。
设另一条垂径的长度为y,则有15 * y = 8 * 8。
解这个方程可以得到y的值,进而求出另一条垂径的长度。
练习题三:在一个半径为10的圆中,一条垂径的长度为24。
求另一条垂径的长度。
解析:同样地,根据圆的垂径定理,垂径的乘积等于半径的平方。
设另一条垂径的长度为z,则有24 * z = 10 * 10。
解这个方程可以得到z的值,进而求出另一条垂径的长度。
通过以上三个练习题,我们可以看到圆的垂径定理的应用。
它告诉我们,对于一个圆来说,任意两条垂径的乘积都等于半径的平方。
这个定理在解决一些几何问题中非常有用。
除了上述练习题,我们还可以通过一些实际问题来应用圆的垂径定理。
例如,
假设有一个圆形花坛,我们想在花坛中心种一棵树。
为了确保树能够均匀地分布在花坛中,我们可以利用垂径定理来确定每棵树之间的最佳位置。
另一个实际应用的例子是在建筑设计中。
如果我们想在一个圆形庭院中建造一个喷泉,我们可以利用垂径定理来确定喷泉的位置,以确保水能够均匀地喷射到庭院的各个角落。
综上所述,圆的垂径定理是一个重要的几何定理,它给出了圆上的垂径之间的关系。
通过练习题和实际应用,我们可以更好地理解和应用这个定理。
无论是解决几何问题还是在实际生活中应用,垂径定理都发挥着重要的作用。
