理学-空间力系习题
空间力系习题答案

空间力系习题答案空间力系习题答案在学习物理学的过程中,空间力系是一个重要的概念。
它描述了物体在空间中受到的各种力的作用情况。
学生们经常会遇到一些关于空间力系的习题,这些习题旨在帮助他们理解和应用这个概念。
在本文中,我将给出一些常见的空间力系习题,并提供详细的解答过程。
1. 一个质量为2kg的物体悬挂在一根长度为1m的细线上,细线的一端固定在天花板上。
求物体受到的重力和细线拉力的大小。
解答:根据题目中给出的信息,可以得知物体受到的重力大小为2kg *9.8m/s^2 = 19.6N。
由于物体处于静止状态,所以细线拉力的大小必须与重力大小相等,即为19.6N。
2. 一个质量为3kg的物体放置在一个倾斜角度为30°的斜面上,斜面的摩擦系数为0.2。
求物体受到的重力分解到斜面上的分力和垂直于斜面的分力的大小。
解答:首先,将重力分解成斜面上的分力和垂直于斜面的分力。
斜面上的分力可以通过将重力乘以斜面的正弦值得到,即3kg * 9.8m/s^2 * sin(30°) ≈ 14.7N。
垂直于斜面的分力可以通过将重力乘以斜面的余弦值得到,即3kg * 9.8m/s^2 * cos(30°) ≈ 25.5N。
接下来,我们需要考虑斜面的摩擦力。
根据题目中给出的摩擦系数和斜面上的分力,可以计算出摩擦力的大小。
摩擦力的大小等于斜面上的分力乘以摩擦系数,即14.7N * 0.2 = 2.94N。
综上所述,物体受到的重力分解到斜面上的分力大小约为14.7N,垂直于斜面的分力大小约为25.5N,斜面对物体的摩擦力大小约为2.94N。
3. 一个质量为4kg的物体放置在一个光滑的水平面上,受到一个水平方向的力为10N和一个竖直向上的力为20N。
求物体受到的合力的大小和方向。
解答:根据题目中给出的信息,可以将水平方向的力和竖直方向的力相互分离。
水平方向的力为10N,竖直方向的力为20N。
首先,我们需要计算水平方向的合力。
第三章空间力系习题解答

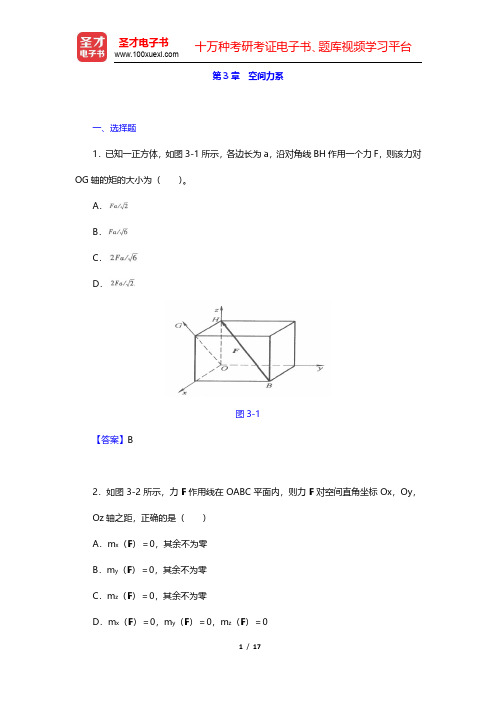
习 题3-1 在边长为a 的正六面体上作用有三个力,如图3-26所示,已知:F 1=6kN ,F 2=2kN ,F 3=4kN 。
试求各力在三个坐标轴上的投影。
图3-26kN 6001111====F F F F z y x0kN245cos kN245cos 2222==︒=-=︒-=z y x F F F F FkN 33433kN 33433kN 33433333333==-=-===F F F F F F z y x3-2 如图3-27所示,已知六面体尺寸为400 mm ×300 mm ×300mm ,正面有力F 1=100N ,中间有力F 2=200N ,顶面有力偶M =20N ·m 作用。
试求各力及力偶对z 轴之矩的和。
图3-27203.03444.045cos 21-⨯+⨯︒-=∑F F M zm N 125.72034240220⋅-=-+-=3-3如图3-28所示,水平轮上A 点作用一力F =1kN ,方向与轮面成a =60°的角,且在过A 点与轮缘相切的铅垂面内,而点A 与轮心O '的连线与通过O '点平行于y 轴的直线成b =45°角,h =r =1m 。
试求力F 在三个坐标轴上的投影和对三个坐标轴之矩。
图3-28N 354N 225045sin 60cos 1000sin cos ==︒⨯︒⨯==βαF F x N 354N 225045sin 60cos 1000cos cos -=-=︒⨯︒⨯-=-=βαF F yN 866350060sin 1000sin -=-=︒⨯-=-=αF F zm N 25845cos 18661354cos ||||)(⋅-=︒⨯⨯-⨯=⨯-⨯=βr F h F M z y x F m N 96645sin 18661354sin ||||)(⋅=︒⨯⨯+⨯=⨯+⨯=βr F h F M z x y Fm N 500160cos 1000cos )(⋅-=⨯︒⨯-=⨯-=r F M z αF3-4 曲拐手柄如图3-29所示,已知作用于手柄上的力F =100N ,AB =100mm ,BC =400mm ,CD =200mm ,a =30°。
第三章空间力系习题解答

3-10如图3-35所示的空间支架。已知:∠CBA=∠BCA=60°,∠EAD=30°,物体的重量为W=3kN,平面ABC是水平的,A、B、C各点均为铰接,杆件自重不计。试求撑杆AB和AC所受的压力FAB和FAC及绳子AD的拉力FT。
图3-35
3-11空间构架由三根直杆铰接而成,如图3-36所示。已知D端所挂重物的重量W=10kN,各杆自重不计。试求杆AD、BD、CD所受的力。
图3-41
3-17曲轴如图3-42所示,在曲柄E处作用一力F=30kN,在曲轴B端作用一力偶M而平衡。力F在垂直于AB轴线的平面内且与铅垂线成夹角a=10°。已知:CDGH平面与水平面间的夹角f=60°,AC=CH=HB=400mm,CD=200mm,DE=EG。不计曲轴自重,试求平衡时力偶矩M之值和轴承的约束反力。
习 题
3-1在边长为a的正六面体上作用有三个力,如图3-26所示,已知:F1=6kN,F2=2kN,F3=4kN。试求各力在三个坐标轴上的投影。
图3-26
3-2如图3-27所示,已知六面体尺寸为400 mm×300 mm×300mm,正面有力F1=100N,中间有力F2=200N,顶面有力偶M=20N·m作用。试求各力及力偶对z轴之矩的和。
图3-36
3-12空间桁架如图3-37所示。力F作用在ABDC平面内,且与铅垂线成45°角,ΔEAK≌ΔFBM,等腰三角形ΔEAK、ΔFBM和ΔNDB在顶点A、B和D处均为直角,又EC=CK=FD=DM。若F=10kN,试求各杆的受力。
图3-37
结点A
结点B
3-13三轮车连同上面的货物共重W=3kN,重力作用点通过C点,尺寸如图3-38所示。试求车子静止时各轮对水平地面的压力。
图3-42
第六章 空间力系 重心 习题

第六章空间力系重心习题概念题:4.14.24.34.44.54.64.74.84.94.104.114.12计算题:4.2 4.34.44.54.6 4.74.8课后习题6-1已知力P大小和方向如图所示,求里P对z轴的矩。
(题6-1图a中的P位于其过轮缘上作用点的切平面内,且与轮平面成α=60度角;图b中的力P位于轮平面内与轮的法线成β=60度角)。
6-2作用于手柄端的力F=600KN,试求计算力在x,y,z轴上的投影及对x,y,z 轴之矩。
6-3图示三脚架的三只角AD,BD,CD各与水平面成60度角,且AB=BC=AC,绳索绕过D处的滑轮由卷扬机E牵引将重物G吊起,卷扬机位于∠ACB的等分线上,且DE与水平线成60度角。
当G=30KN时被等速地提升时,求各角所受的力。
6-4重物Q=10KN,由撑杆AD及链条BD和CD所支持。
杆的A端以铰链固定,又A,B和C三点在同一铅垂墙上。
尺寸如图所示,求撑杆AD和链条BD,CD 所受的力(注:OD垂直于墙面,OD=20cm)。
6-5固结在AB轴上的三个圆轮,半径各为r1,r2,r3;水平和铅垂作用力大大小F1=F1’,F2=F2’为已知,求平衡时F3和F3’两力的大小。
6-6平行力系由5个力组成,各力方向如图所示。
已知:P1=150N,P2=100N,P3=200N,P4=150N,P5=100N。
图中坐标的单位为cm。
求平行力系的合力。
6-7有一齿轮传动轴如图所示,大齿轮的节圆直径D=100mm,小齿轮的节圆直径d=50mm。
如两齿轮都是直齿,压力角均为α=20度,已知作用在大齿轮上的圆周力P1=1950N,试求转动轴作匀速转动时,小齿轮所受的圆周力P2的大小及两轴承的反力。
6-8一减速机构如图所示,动力由I轴输入,通过连轴节在I轴上作用一力偶,其矩为m=697NM,如齿轮节圆直径为D1=160mm,D2=632mm,D3=204mm,齿轮压力角为20度,试求Ⅱ轴两端轴承A,B的约束反力。
哈工大理论力学教研室《理论力学Ⅰ》(第7版)章节题库-空间力系(圣才出品)
矩。已知:F=1kN,a=18cm,b=c=10cm。
图 3-6 解:解法一:利用力对点之矩与力对轴之矩的关系定理来计算。由于 CD 轴和 CE 轴均 过 C 点,因此可以先计算力对 C 点之矩,再将其分别向 CD 轴和 CE 轴投影来求解。
4 / 17
圣才电子书 十万种考研考证电子书、题库视频学习平台
1 17
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 3-2 【答案】C 【解析】先计算 F 在各轴上的投影大小
Fx = −F cos30。cos 60。, Fy = −F cos30。sin 60。, Fz = F sin 30。
再计算对各轴的矩
3.有重力为 W、边长为 a 的均质正方形薄板,与—重力为 0.75W、边长分别为 a 和 2a 的直角均质三角形薄板组成的梯形板,如图 3-3 所示。其重心的坐标(xc,yc)为( )。
A. B. C. D.
2 / 17
圣才电子书 十万种考研考证电子书、题库视频学习平台
【答案】B
图 3-3
二、填空题 1.空间力系若不平衡,其简化的最后结果:或者是一个力,或者是______;或者是 ______。 【答案】一个力偶;一个力螺旋 【解析】空间任意力系简化的最终结果有 4 种情况:合力、合力偶、力螺旋和平衡。当 主矢不为零,主矩为零或主矩不为零但主矢主矩垂直时,最终结果为合力;当主矢主矩均不 为零,主矢与主矩平行或成任意角(不包括垂直角度时),最终结果为力螺旋;当主矢为零 主矩不为零时,最终结果为合力偶;当主矢主矩均为零时,力系平衡。
(1)先将力 F 分解为沿坐标轴的三个分力如图 3-6(b)所示,其中有
代入数据可计算出
(2)计算力对过 C 点的三根正交轴之矩,因为有
理论力学---第四章空间力系习题

例4-11
已知:F、P及各尺寸
求: 杆内力
解:研究对象,长方板,列平衡方程
M
AB AE
F 0 F 0
F6 a
a 2
P 0 F6
F5 0
P 2
F D y 1 3 .0 3 K N
例 已知:各边长,载荷P、Q。 求:各杆的约束反力。 解:(1)考虑板的平衡,各杆均 为二力杆,设均受拉力。 (2)画受力图,建立坐标系,注 意各矢量的空间关系。 (3)列写平衡方程,空间一般力系有6个方程,尽量使 一个方程包含一个未知数。
M M
AB
F2 b
P F3 cos 45 b 0
F3 2 2 P
汽车后半桥传动轴,如图所示,A 处是向心推力轴承 (止推轴承),B 处是向心轴承(颈轴承)。设汽车匀 速直线行驶(平衡)。 已知:地面法向反力FD = 20 kN,锥齿轮上受的三个力 Ft = 117(kN),Fr = 36 kN,Fa =22.5 kN。齿轮节圆直 径 d = 98 mm,车轮半径R = 440 mm,尺寸如图。 求: 地面的摩擦力及两轴承的约束反力。
FOx Fx 0
F
y
0
FOy Fy 0
F
z
0
FOz Fz 0
100 FZ M x 0
30 FZ M y 0
100 Fx 30 Fy M z 0
M F 0
x
M F 0
y
M F 0
z
FOx 4.25kN, FOy 6.8kN, FOz 17kN
空间力系(理论力学电子教程)

力矩关系定理:力对于任一点之矩矢在通过该点的任一轴上 的投影等于力对于该轴之矩。
M o ( F ) cos M z ( F ) [M o ( F )]Z
应用上述定理可以求出力对于坐标轴之矩的解析表达式。
M0 ( F ) r F (yz zy) i (yz xz) j (zy yz) k
该力系的多边形2选择题1空间力偶矩是a代数量b滑动矢量c定位矢量d自由矢量讨论与分析理论力学电子教程第四章空间力系2一空间力系中各力的作用线均平行于某一固定平面而且该力系又为平衡力系则可列独立平衡方程的个数是3如果一空间力系中各力的作用线分别汇交于两个固定点则当力系平衡时可列独立平衡方程的个数是4如图所示矩形板重p用球铰链c以及柔绳bd支承在水平面上则力理论力学电子教程第四章空间力系理论力学电子教程第四章空间力系3如图所示曲杆abcdabbcbcdc
理论力学电子教程
第四章 空间力系
由于 z1 轴垂直于y 轴,所以根据合力投影定理可得
Fz F xcos 2 Fz cos 1
1
a a c c F 2 2 F 2 2 2 2 2 2 2 a b c a c a b c a c2
a2 c2 F 2 64 N 2 2 2 2 a b c a c
F1
A2
x
FR F' F F' R
x
Mo M M0 ( F ) M0
空间任意力系向任一点简化的结果。一般可得到一力和一力偶, 该力作用于简化中心,其力矢等于力系的主矢,该 力偶 的力偶矩矢等于力系对于简化中心的主矩。
理论力学电子教程
第四章 空间力系
与平面力系一样,空间力系的主矢与简化中心的位置无关, 而矩的一般将随着简化中心的位置不同而改变。
理论力学第6讲空间基本力系

x
x
F
Fx Fy Fz 4.52 6.32 182
2 2 2
Fy y
α β γ
19.6 kN
力F的方向
cos
cos
Fz
Fx F
Fy F Fz
4.5 19.6
6.3 19.6 18
0.220 ,
0.322 ,
7641'
z
F
717'
点O,其上作用有铅直载荷F。钢丝OA和OB所构成的平面垂直于铅直平面 Oyz,并与该平面相交于OD,而钢丝OC则沿水平轴y。已知OD与轴z间的夹
角为β,又∠AOD = ∠BOD = α,试求各钢丝中的拉力。
第五章 空间基本力系
例题 5-3
§5–3 空间共点力系合成的解析法及其平衡的解析条件
例题 5-3
§5–4 力 偶 矩 矢
力偶作用面的平移
力偶作用面的平移
第五章 空间基本力系
§5–4 力 偶 矩 矢
2. 力偶矩矢
(1) 概念: 用来表示力偶矩的大小、转向、作用面方位的有向线段。
(2) 力偶的三要素:
力偶矩的大小。 力偶的转向。 力偶作用面的方位 (3) 符号:M
M1
M2
第五章 空间基本力系
cos M , k
0.262 , M , j 74.8
0.965 , M , k 15.2
M Mz
M
45°
O
4. 为使这个刚体平衡,需加一力
偶,其力偶矩矢为 M4= -M 。
第五章 空间基本力系
x
§2–9 空间力偶系的合成和平衡条件
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间力系习题第四章空间力系4-1 力系中,F 1=100 N 、F 2=300 N 、F 3=200 N ,各力作用线的位置如图所示。
试将力系向原点O 简化。
解:由题意得N 34552200132300R -=?-?-=x FN 250133300R =?=y F N 6.1051200100R =?-=z Fm N 8.513.0512001.0133300?-=??-??-=x Mm N 6.361.013220020.0100?-=??+?-=y Mm N 6.1033.0522002.0133300?=??+??=z M 主矢N 4262R 2R 2R R =++=x y z F F F F ,N )6.10250345(R k j i ++-=F主矩m N 122222?=++=z y x O M M M M ,m N )1046.368.51(?+--=k j i O M4-3 图示力系的三力分别为N 3501=F 、N 4002=F 和N 6003=F ,其作用线的位置如图所示。
试将此力系向原点O 简化。
解:由题意得N 144216001810060350'R -=?-?=x F N1010866.0600707.04001810080350'R =?+?+?=y FN 517707.04001810090350'R -=?--?=z F主矢N 11442'R 2'R 2'R R =++=z y x F F F 'F ,N )5171011144(R k j i F -+-=';m N 48mm N48000120707.0400601810090350?-=?-=??-??-=x M m N 07.21mm N 21070901810090350?=?=??=y M 602160090866.0600601810060350901810080350??+??-??-??=z M m N 4.19mm N 19400?-=?-=主矩m N 55.9mm N 55900222?=?=++=z y x O M M M Mm N )4.191.2148(?-+-=k j i M O4-5 轴AB 与铅直线成α角,悬臂CD 与轴垂直地固定在轴上,其长为a ,并与铅直面zAB 成θ角,如图所示。
如在点D 作用铅直向下的力F ,求此力对轴AB 的矩。
解:将力F 分解为F 1、F 2两个力,F 1垂直于AB 而与CE 平行,F 2平行于AB如图(a )。
这两个分力分别为:αs i n 1F F =,αcos 2F F =)()()(21F M F M F M AB AB AB +=0s i n 1+?=θa F θαs i n s i n Fa =4-7 图示空间构架由三根无重直杆组成,在D 端用球铰链连接,如图所示。
A 、B 和C 端则用球铰链固定在水平地板上。
如果挂在D 端的物重W =10 kN ,试求铰链A 、B 和C 的反力。
解:取节点D 为研究对象,假设各杆都为拉力、受力如图(a )。
平衡方程为:0=∑x F ,045cos 45cos =?-?A B T T (1)0=∑y F ,015cos 30cos 45sin 30cos 45sin =?-??-??-C B A T T T (2)0=∑z F ,015sin 30sin 45sin 30sin 45sin =-?-??-??-T T T T C B A(3)把T=W =10 kN 代入式(3)解出:kN 4.26-==B A T T (压力)kN 5.33=C T (拉力)4-9 图示空间桁架由六杆1、2、3、4、5和6构成。
在节点A 上作用一力F ,此力在矩形ABDC 平面内,且与铅直线成45°角。
FBM EAK ?=?。
等腰三角形EAK 、FBM 和NDB 在顶点A 、B 和D 处均为直角,又EC=CK=FD=DM 。
若F =10 kN ,求各杆的内力。
解:一、取节点A 为研究对象,受力图及坐标如图(a )。
0=∑x F ,045cos )(21=?-S S (1)0=∑y F ,045sin 3=?+F S(2)0=∑z F ,045cos 45sin )(21=?-?+-F S S(3)解出:kN 5221-=-==FS S ,kN 07.73-=S 二、取节点B 为研究对象,受力如图(a )。
0=∑x F ,045cos )(54=?-S S (4)0=∑y F ,045sin 36=-?S S(5)0=∑z F ,045sin )(654=?++-S S S(6)解出:kN 554==S S (拉力),kN 106-=S (压力)4-11 图示三圆盘A 、B 和C 的半径分别为150 mm 、100 mm 和50 mm 。
三轴OA 、OB 和OC 在同一平面内,AOB ∠为直角。
在这三圆盘上分别作用力偶,组成各力偶的力作用在轮缘上,它们的大小分别等于10 N 、20 N 和F 。
如这三圆盘所构成的物系是自由的,不计物系重量,求能使此物系平衡的力F 的大小和角α。
解:画出三个力偶的力偶矩矢如图(a ),由力偶矩矢三角形图(b )可见:mm N 5000400030002222?=+=+=B AC M M M由图(a )100?=F M C ,N 50100==CM F 由图(b )可知:43tan ==BAM M β,'523687.36?=?=β '08143180?=-?=βα4-13 如图所示,已知镗刀杆刀头上受切削力500=z F N ,径向力150=x F N ,轴向力75=y F N ,刀尖位于Oxy 平面内,其坐标x =75 mm, y =200 mm 。
工件重量不计,试求被切削工件左端O 处的约束反力。
解:取镗刀杆为研究对象,受力如图(a )所示。
0=∑x F ,0=+-Ox x F F (1)0=∑y F ,0=+-Oy y F F (2)0=∑z F ,0=+-Oz z F F (3)0=∑x M ,02.0=+?-x z M F(4)0=∑y M ,0075.0=+?y y M F(5)0=∑z M ,0075.02.0=+?-?z y x M F F(6)解得:N 150=ox F ,N 75=oy F ,N 500=oz F ;m N 100?=x M ,m N 5.37?-=y M (与原始反向),m N 4.24?-=z M (与原始反向)4-15 某减速箱由三轴组成如图所示,动力由I 轴输入,在I 轴上作用转矩M1=697 N ?m 。
如齿轮节圆直径为D 1=160 mm ,D 2=632 mm ,D 3=204 mm ,齿轮压力角为20°。
不计摩擦及轮、轴重量,试求等速传动时,求轴承A 、B 、C 、D 的约束反力。
解:(一)研究对象:AB 轴,受力图(a )0=∑y M 11τ2M D F =?N 5.871216.06972211τ=?=?D M F 又αc o s τF F =,N 3171tan sin ττ===ααF F F 0=∑x M ,0580200=-?Bz F F τN 30042910τ==F F Bz0=∑z F ,0=+--τF F F Bz AzN 5708=Az F0=∑z M ,0580200r =?+?-Bx F FN 1093=Bx F0=∑x F ,0r =-+Bx Ax F F FN 2078-=Ax F(二)研究对象:CD 轴,受力图(b )0=∑y M ,02'2'3t32τ=-D F D F N 269925.8712204632'τ32τ3=?==F D D FN 982420tan t3t3=?=F F0=∑x M ,0580435200't3τ=?-?-?-D z F F F0580435269922005.8712=?+?-?-Dz F ,N 23248-=Dz F 0=∑z F ,0't3t =---D z Cz F F F F ,N 12456=Cz F 0=∑z M ,0580435200'r3r =?+?-?D x F F F058043598242003171=?+?-?D x F ,N 6275=Dx F0=∑x F ,0'r3r =-+-D x Cx F F F F ,N 378-=Cx F4-17 如图所示,均质长方形薄板重W =200 N ,用球铰链A 和蝶铰链B 固定在墙上,并用绳子CE 维持在水平位置。
求绳子的拉力和支座反力。
解:取薄板为研究对象,受力如图(a )。
尽量采用力矩式求解。
0=∑z M ,0=?-AB F Bx ,0=Bx F 0=∑AC M ,030sin =??AB F Bz ,0=Bz F 0=∑y M ,0230sin =?+??-BCW BC T N 200==W T0=∑BC M ,02=?-?AB F ABW Az N 1002==W F Az0=∑x F ,030sin 30cos =??-T F Ax ,N 6.86=Ax F 0=∑y F ,030cos 2=?-T F Ay ,N 150=Ay F4-19 无重曲杆ABCD 有两个直角,且平面ABC 与平面BCD 垂直。
杆的D 端为球铰支座,另一A 端受轴承支持,如图所示。
在曲杆的AB 、BC 和CD 上作用三个力偶,力偶所在平面分别垂直于AB 、BC 和CD 三线段。
已知力偶矩2M 和3M ,求使曲杆处于平衡的力偶矩1M 和支座反力。
解:取曲杆为研究对象,受力图及坐标系如图(a )所示。
平衡方程为:0=∑x F ,0=Dx F (1)0=∑y F ,0=+Dy Ay F F (2)0=∑z F ,0=+Dz Az F F (3)0=∑x M ,01=?-?-b F c F M Az Ay (4)0=∑y M ,02=-?M a F Az (5)0=∑z M ,03=?-a F M Ay(6)由式(5)、(6)解出:a MF Az 2=,aM F Ay 3=代入式(2)、(3),得:a M F Dy 3-=,aMF Dz 2-=再代入式(4),得:231M abM a c M +=,即0321=--cM bM aM(7)从图上看,在直角系中,)(321k j i M M M M +-=)(k j i DA c b a +--=式(7)表示,0=?-DA M ,即DA M ∠,M 只有满足此式才能使曲杆达到平衡。
