第二节 二重积分的计算法(一)..
合集下载
第二节 二重积分的计算
2
a
O
a
a
0
2a
x
原式= dy
a a2 y2 f ( x, y2 2a
2 2
y ) dx
2a 2a y2 f 2a
dy
0
a
2a
a a y
f ( x , y )dx dy
a
( x , y ) dx
19
二重积分的计算法
交换积分次序的步骤
(1) 将已给的二次积分的积分限得出相
计算结果一样. 但可作出适当选择.
a
b
x
11
二重积分的计算法
(4) 若区域如图, 则必须分割.
y
D1
在分割后的三个区域上分别 使用积分公式.
(用积分区域的可加性质)
O
D3
D2
x
D
D
1
D2 D3
D1、D2、D3都是X型区域
12
二重积分的计算法
例 求 ( x 2 y )dxdy , 其中D是抛物线 y x 2和
R
R
dy
R2 y2
R 2 x 2 y 2 dx
8
二重积分的计算法
注 特殊地 D为矩形域: a≤x≤b,c≤y≤d
则
f ( x , y )d dx f ( x , y )dy a c D dy f ( x, y ) d x
d b c a
b
d
如D是上述矩形域, 且f ( x , y ) f1 ( x ) f 2 ( y ) 则
立体的体积.
D
曲顶z R 2 x 2
z
解 V1 f ( x , y ) d
a
O
a
a
0
2a
x
原式= dy
a a2 y2 f ( x, y2 2a
2 2
y ) dx
2a 2a y2 f 2a
dy
0
a
2a
a a y
f ( x , y )dx dy
a
( x , y ) dx
19
二重积分的计算法
交换积分次序的步骤
(1) 将已给的二次积分的积分限得出相
计算结果一样. 但可作出适当选择.
a
b
x
11
二重积分的计算法
(4) 若区域如图, 则必须分割.
y
D1
在分割后的三个区域上分别 使用积分公式.
(用积分区域的可加性质)
O
D3
D2
x
D
D
1
D2 D3
D1、D2、D3都是X型区域
12
二重积分的计算法
例 求 ( x 2 y )dxdy , 其中D是抛物线 y x 2和
R
R
dy
R2 y2
R 2 x 2 y 2 dx
8
二重积分的计算法
注 特殊地 D为矩形域: a≤x≤b,c≤y≤d
则
f ( x , y )d dx f ( x , y )dy a c D dy f ( x, y ) d x
d b c a
b
d
如D是上述矩形域, 且f ( x , y ) f1 ( x ) f 2 ( y ) 则
立体的体积.
D
曲顶z R 2 x 2
z
解 V1 f ( x , y ) d
二重积分的计算法
b
( x)
( x)
( x)
f ( x, y ) d y 2
( x)
0
f ( x, y ) d y
( x)
f ( x, y ) d y
y
f ( x, y) d y
2
[2
a
b
( x)
0
f ( x, y ) d y ]d x 2
若 f ( x , y) f ( x, y), 则 ( x ) f ( x, y ) d y 0 ( x) b 则 D f ( x, y) d a 0 d x 0 当区域关于 y 轴对称, 函数关于变量 x 有奇偶性时, 仍 在第一象限部分, 则有 2 2 ( x y ) d x d y D ( x y ) d x d y 0
1
(2) f ( x , y) f ( x, y), 则 f ( x, y ) d 0
D
( x)
证明域D 关于x 轴对称,故不妨记为 则
0 y ( x ) D1 : a xb
( x) y ( x) a xb
故
D1
f ( x, y ) d
b
a
d x
( x)
0
f ( x, y) d y
D f ( x, y) d a d x ( x ) f ( x, y ) d y
b
( x)
若 f ( x , y) f ( x, y), 则
则 D f ( x, y ) d d x a
x
结束
(3)对称性 在闭区域上连续, 域D 关于x 轴对称, 设函数 y D 位于 x 轴上方的部分为D1 , 在 D 上 ( x) (1) f ( x , y) f ( x, y), 则 D1 b D f ( x, y) d 2D f ( x, y) d a o D x
( x)
( x)
( x)
f ( x, y ) d y 2
( x)
0
f ( x, y ) d y
( x)
f ( x, y ) d y
y
f ( x, y) d y
2
[2
a
b
( x)
0
f ( x, y ) d y ]d x 2
若 f ( x , y) f ( x, y), 则 ( x ) f ( x, y ) d y 0 ( x) b 则 D f ( x, y) d a 0 d x 0 当区域关于 y 轴对称, 函数关于变量 x 有奇偶性时, 仍 在第一象限部分, 则有 2 2 ( x y ) d x d y D ( x y ) d x d y 0
1
(2) f ( x , y) f ( x, y), 则 f ( x, y ) d 0
D
( x)
证明域D 关于x 轴对称,故不妨记为 则
0 y ( x ) D1 : a xb
( x) y ( x) a xb
故
D1
f ( x, y ) d
b
a
d x
( x)
0
f ( x, y) d y
D f ( x, y) d a d x ( x ) f ( x, y ) d y
b
( x)
若 f ( x , y) f ( x, y), 则
则 D f ( x, y ) d d x a
x
结束
(3)对称性 在闭区域上连续, 域D 关于x 轴对称, 设函数 y D 位于 x 轴上方的部分为D1 , 在 D 上 ( x) (1) f ( x , y) f ( x, y), 则 D1 b D f ( x, y) d 2D f ( x, y) d a o D x
第二节 二重积分的计算法(一)
例1 计算 xyd , D 其中D为y2 =x 和y =x2 所围的闭区域.
解: D为X－型区域
D 0 x 1, x 2 y
1 x
2
x
xyd 0 dx x xydy
D
y 1 y=x2
y x
y 0 x dx 2 x
1 2
2
x
1 1 2 5 0 ( x x )dx 2
0 dx 0 f ( x , y )dy
y=x D x
1
1
x
f ( x , y )dxdy
D
0
0 dy y f ( x , y )dx
1 1
例5 改换二次积分 0 dy 0
1
2 y y2
f ( x , y )dx 的积分次序.
解： D : 0 x
2 y y2 ,0 y 1
x
z=f (x, y)
A( x)
D
2 ( x )
1( x)
f ( x , y )dy
f ( x , y )d
a [ ( x ) f ( x , y )dy ]dx
b
1
A( x)
1(x)
y
2(x)
2 ( x )
a dx ( x ) f ( x , y )dy
1 2
先交换交换顺序
1 1 cos 1 2
例7 计算I
x e
2 D
y2
dxdy ,
其中D为x 0, y 1, y x围成。
解 区域D既是X－型，又是Y－型的
e 的原函数不是初等函数。
y2
y
y=1
0902二重积分的计算法-1
D
b ϕ2( x) f ( x , y )dy ; = dx a ϕ1 ( x )
∫
∫∫ f ( x , y )dσ ∫
D
d ϕ2 ( y) f ( x , y )dx . = dy c ϕ1 ( y )
∫
［混合型］ 混合型］ （在积分过程中要正确选择积分次序） 在积分过程中要正确选择积分次序） 积分次序
y
A(x)
a
x
y = ϕ2 ( x)
b
x
D
y = ϕ1( x)
b ϕ ( x) ∴ ∫∫ f ( x , y )dσ =∫a dx ∫ϕ 2( x ) f ( x , y )dy . ……二次积分公式 ? 1 二次积分公式
D
◆如果积分区域为：c ≤ y ≤ d , ϕ1 ( y ) ≤ x ≤ ϕ 2 ( y ). 如果积分区域为：
π
练习1 练习 改变下列积分的积分次 序
∫
1 2 x− x2 2 2− x dx f ( x , y )dy + dx f ( x , y )dy . 0 0 1 0
∫
∫
∫
解 积分区域如图： 积分区域如图：
y = 2− x
原式 = ∫0 dy ∫
1
2− y
2
y = 2x − x2
1− 1− y
f ( x , y )dx.
1
o
1
x
2.设f ( x , y )在D上连续 , 其中 D是由直线 y = x , y = a及x = b (b > a )所围成的闭区域 , 证明 :
(1)∫
b x dx a a
∫ f ( x , y )dy = ∫
b b dy y a
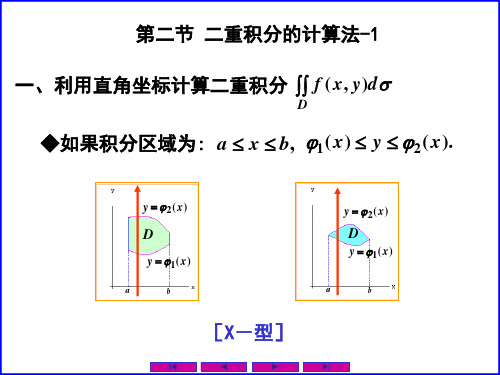
b ϕ2( x) f ( x , y )dy ; = dx a ϕ1 ( x )
∫
∫∫ f ( x , y )dσ ∫
D
d ϕ2 ( y) f ( x , y )dx . = dy c ϕ1 ( y )
∫
［混合型］ 混合型］ （在积分过程中要正确选择积分次序） 在积分过程中要正确选择积分次序） 积分次序
y
A(x)
a
x
y = ϕ2 ( x)
b
x
D
y = ϕ1( x)
b ϕ ( x) ∴ ∫∫ f ( x , y )dσ =∫a dx ∫ϕ 2( x ) f ( x , y )dy . ……二次积分公式 ? 1 二次积分公式
D
◆如果积分区域为：c ≤ y ≤ d , ϕ1 ( y ) ≤ x ≤ ϕ 2 ( y ). 如果积分区域为：
π
练习1 练习 改变下列积分的积分次 序
∫
1 2 x− x2 2 2− x dx f ( x , y )dy + dx f ( x , y )dy . 0 0 1 0
∫
∫
∫
解 积分区域如图： 积分区域如图：
y = 2− x
原式 = ∫0 dy ∫
1
2− y
2
y = 2x − x2
1− 1− y
f ( x , y )dx.
1
o
1
x
2.设f ( x , y )在D上连续 , 其中 D是由直线 y = x , y = a及x = b (b > a )所围成的闭区域 , 证明 :
(1)∫
b x dx a a
∫ f ( x , y )dy = ∫
b b dy y a
第九章第2节二重积分的计算(1)
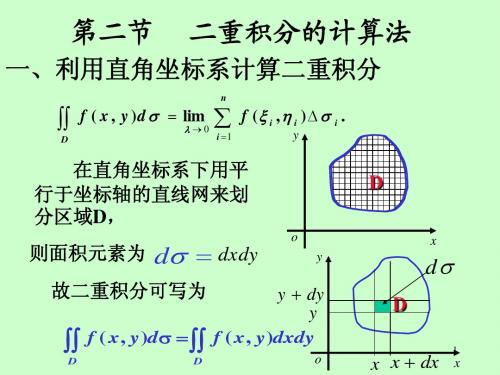
y + dy y ∫∫ f ( x, y)dσ =∫∫ f ( x, y)dxdy
D D
dσ
D
x
o
x x + dx
1
x
直角坐标系下的计算公式
a 如果积分区域为： 如果积分区域为： ≤ x ≤ b, ϕ 1 ( x ) ≤ y ≤ ϕ 2 ( x ).
y = ϕ2 ( x )
y = ϕ2 ( x )
ϕ1 ( x )
f ( x , y )dy
4
如果积分区域为： 如果积分区域为：
c ≤ y ≤ d , ϕ 1 ( y ) ≤ x ≤ ϕ 2 ( y ).
d
d
x = ϕ1 ( y )
D
x = ϕ2 ( y)
x = ϕ1 ( y )
D
c
c
x = ϕ2 ( y)
∫∫ f ( x , y )dσ = ∫
π
例4. 求 ∫∫ x e
D
2 − y2
dxdy ，其中 D 是以(0,0), (1,1),
(0,1)为顶点的三角形.
解 Q∫ e
− y2
dy 无法用初等函数表示
∴ 积分时必须考虑次序
∫∫ x e
D
2 − y2
dxdy = ∫ dy ∫ x e
0 0
1
y
2 − y2
dx
=∫ e
0
1
− y2
y ⋅ dy = − 3
2 2 2
2
2
2
利用对称性, 考虑第一卦限部分, 其曲顶柱体的顶为
R
o x
R2 −x2
x2 + y2 = R2
z = R2 − x2 0 ≤ y ≤ R2 − x2 (x, y) ∈D: 0 ≤ x ≤ R
二重积分的计算1
z
y
D
z = f (x, y)
O
a x0 b x
目录 上页 下页 返回 结束
设曲顶柱的底为
y = ϕ2 (x)
z z = f (x, y)
ϕ1(x) ≤ y ≤ ϕ2 (x) D = (x, y) a ≤ x ≤b
任取 截面积为 故曲顶柱体体积为 平面 截柱体的
y
D
O
a x0 b x y = ϕ1(x)
D
x
∫c d y∫ψ ( y)
1
d
ψ 2 ( y)
c f (x, y) dx O =ψ ( y) x x 1
当被积函数 f (x, y) 在D上变号 变号时,结论仍成立。 变号
目录 上页 下页 返回 结束
说明: 说明 (1) 若积分区域既是 X - 型区域又是Y - 型区域 , 则有
∫∫D
b a d
V = ∫∫ f (x, y) dσ = ∫ A(x)记 d x
ϕ2 (x) f (x,y) dy ]d x = d x = [ f (x,y)dy a ϕ1( x) a ϕ1(x)
b
∫ ∫
D b ϕ2 ( x)
a
作
∫
b
∫
目录
上页
下页
返回
结束
同样, 曲顶柱的底为
D = { (x, y) ψ1( y) ≤ x ≤ψ2 ( y), c ≤ y ≤ d }
−4
y
−2
y2 = x
x
y
=[
12y − 1 y2 − 1 y3 2 3
D
注: 计 ∫∫ 算
2 ] −[ ] = 52 3 −4 −2 f (x, y) dσ 时 若 f (x, y) 可 展 D , 扩 到 1
y
D
z = f (x, y)
O
a x0 b x
目录 上页 下页 返回 结束
设曲顶柱的底为
y = ϕ2 (x)
z z = f (x, y)
ϕ1(x) ≤ y ≤ ϕ2 (x) D = (x, y) a ≤ x ≤b
任取 截面积为 故曲顶柱体体积为 平面 截柱体的
y
D
O
a x0 b x y = ϕ1(x)
D
x
∫c d y∫ψ ( y)
1
d
ψ 2 ( y)
c f (x, y) dx O =ψ ( y) x x 1
当被积函数 f (x, y) 在D上变号 变号时,结论仍成立。 变号
目录 上页 下页 返回 结束
说明: 说明 (1) 若积分区域既是 X - 型区域又是Y - 型区域 , 则有
∫∫D
b a d
V = ∫∫ f (x, y) dσ = ∫ A(x)记 d x
ϕ2 (x) f (x,y) dy ]d x = d x = [ f (x,y)dy a ϕ1( x) a ϕ1(x)
b
∫ ∫
D b ϕ2 ( x)
a
作
∫
b
∫
目录
上页
下页
返回
结束
同样, 曲顶柱的底为
D = { (x, y) ψ1( y) ≤ x ≤ψ2 ( y), c ≤ y ≤ d }
−4
y
−2
y2 = x
x
y
=[
12y − 1 y2 − 1 y3 2 3
D
注: 计 ∫∫ 算
2 ] −[ ] = 52 3 −4 −2 f (x, y) dσ 时 若 f (x, y) 可 展 D , 扩 到 1
第二节_二重积分的计算法
第二节_二重积分的计算法二重积分：在平面上规定一个有界闭合区域D，对于D上的每一点P(x,y)，都有一个标量函数f(x,y)与之对应。
则二重积分的数值就是由函数f(x,y)在区域D上所有点处的函数值决定的。
二重积分一般可以表示为∬Df(x,y)dA。
计算二重积分的方法主要有以下几种：直角坐标法、极坐标法、换元积分法和累次积分法。
1.直角坐标法：针对矩形、直角三角形、抛物线和折线边界的区域，可以直接使用直角坐标法来计算二重积分。
具体步骤如下：(1)写出二重积分的累加和形式：I=ΣΣf(x,y)ΔA。
(2)将区域D分成若干小矩形，计算每个小矩形的面积ΔA。
(3)在每个小矩形上选择代表点(x,y)，计算f(x,y)的函数值。
(4)将函数值与相应小矩形的面积相乘，加和求和即可得到二重积分的数值。
2.极坐标法：当具有极坐标对称性的区域时，采用极坐标法可以简化计算。
具体步骤如下：(1) 确定极坐标变换：x=r*cosθ，y=r*sinθ。
(2) 根据变换的雅可比矩阵计算面积元素dA的极坐标形式：dA=rdrdθ。
(3) 将二重积分转化为极坐标下的累次积分：I=∫∫Df(x,y)dxdy=∫∫Df(r*cosθ,r*sinθ)rdrdθ。
(4)将极坐标下的积分区域和积分限进行变换，然后按照累次积分进行计算。
3.换元积分法：当二重积分区域D的边界方程比较复杂时，可以使用换元积分法来简化计算。
具体步骤如下：(1)根据边界方程对二重积分区域D进行变换，将原来的二重积分区域映射到一个新的坐标系中的区域G。
(2)根据变换的雅可比矩阵，计算新坐标系下的面积元素dA'。
(3) 将二重积分转化为新坐标系下的累次积分：I=∫∫Df(x,y)dxdy=∫∫Gf(x(u,v),y(u,v))，J(u,v)，dudv，其中J(u,v)为雅可比行列式。
(4)对新坐标系下的累次积分按照直角坐标法或极坐标法进行计算。
4.累次积分法：当二重积分区域D可以通过垂直于坐标轴的直线进行划分时，可以使用累次积分法进行计算。
10.2二重积分的计算(1)
xydx]dy
2
1
[
y
x2 ] y dy 21
2
1
[
y3 2
y ]dy 2
y4 [
8
y2 4
]
12
1
1 8
.
例 2 计算 y 1 x2 y2d , 其中 D 是由直线 D
y x、x 1和 y 1 所围成的闭区域.
解 如图, D 既是 X 型, 又是Y 型.若视为X
型, 则
11
原积分 [ y 1 x2 y2dy]dx 1 x
第二节 二重积分的计算法（1）
一、利用直角坐标系计算二重积分 二、交换二次积分次序 三、对称性、奇偶性的应用
一、利用直角坐标系(right angle coordinate system)计算二重积分
如果积分区域为：a x b, 1( x) y 2( x).
［X－型］
y 2(x)
D
y 1( x)
y2 x 及直线 y x 2所围成的闭区域.
解 如图,
D 既是 X 型, 也是Y 型. 但易见选择前者计算
较麻烦, 需将积分区域划分为两部分来计算, 故选
择后者.
2 y2
xyd
[ 1 y2
xydx]dy
D
2 [ x2 1 2
y]
y y2
2
dy
1 2
2
[ y( y 2)2 y5 ]dy
)(e
y
1 0
)
(e
1)2 .
例 6 求两个底圆半径都等于 R 的直交圆柱面所围
成的立体的体积.
解 设两个圆柱面的方程分别为 x2 y2 R2 及
d
dy
2 ( y) f ( x, y)dx.
第二节二重积分的计算方法
r4 4
)
|ba
d
(b4 a4 )
2
例7 计算 ex2 y2 dxdy
D
D : x2 y2 a2
ex2y2 dxdy
2
d
a er2 rdr
0
0
D
2 0
(
er2 2
) |0a
d
(1 ea2 )
此题若采用直角坐标系方法无法积分
例8.化为极坐标形式: 2R
2R
2Ry y2
0 dy0
d
D
f (x, y)dxdy
d
[cΒιβλιοθήκη x2 ( y) x1 ( y)
f (x, y)dx]dy
x x1(y) D c
f (x, y)dxdy
d
dy
x2 ( y) f (x, y)dx
D
c
x1 ( y)
x x2(y)
先对x 后对y 的二次积分
注:(1).如果D 既是X 型域又是Y 型域,则
0
2
5.
arctan y d
4 d
2
rdr
4 d
2 rdr 3 2 .
D
x
0
1
0
1
64
1 x2 y2 4, y x, y 0围成的第一象限的区域
6.
sin x2 y2 d
2
2
d sin rdr 4.
D
x2 y2
0
1
1 x2 y2 4
7. D
f (x, y)dx
2 R sin
0
2 d
f (r cos , r sin )rdr
0
0
注意:下列情形适合用极坐标计算: (1).积分区域适于极坐标表示,例如:圆,圆环; (2).被积函数形如 f (x2 y2 ); (3).用直角坐标系计算不出时.
二重积分的计算
y = 1 − x. 所以
∫∫ ∫ ∫ f (x, y)dσ =
1
1− x
dx f (x, y)dy.
0
0
D
y
同理
∫∫ ∫ ∫ f (x, y)dσ =
1
dy
1− y
f (x, y)dx.
0
0
D
x+ y =1
O
x
3.∫∫ f (x, y)dxdy. 其中 D = {(x, y) 0 ≤ y ≤ x, 0 ≤ x ≤ 1}. D
例7.5 交换下列积分次序
1
x2
1.∫0 dx∫0 f (x, y)dy.
解 积分区域如图所示, 所以
1
x2
∫0 dx∫0 f (x, y)dy
1
1
= ∫0 dy∫ y f (x, y)dx.
y
y = x2, x = y
1
D O 1x
∫∫ 例7.6 计算积分 xydσ, 其中D由 y = 1, y = x, x = 2 D
一、利用直角坐标系计算二重积分
利用直角坐标计算二重积分的关键是将二重积 分化为二次积分. 如果积分区域为： a ≤ x ≤ b, ϕ1( x) ≤ y ≤ ϕ2( x).
［X－型］
y = ϕ2(x)
D
y = ϕ1(x)
y = ϕ2(x)
D
y = ϕ1( x)
a
b
a
b
其中函数ϕ1( x) 、ϕ2( x) 在区间 [a,b]上连续.
1.将区域投影至 x轴, 得区间[a,b];
2.由 x = a, x = b得区域的上、下边界曲线 y = ϕ2 ( x),
y = ϕ1 ( x), 则
二重积分计算1
y2x y 2xx2
原 式 0 1d1 2 y y 1 y2f(x ,y)d.x
例 3改 变 积 分 0 2adx2 2a a x xx2f(x,y)dy(a0)
的 次 序 .
解：
2a
y 2ax
a
y 2axx2 xaa2y2
a 2a
= 原式
D
a 1(x)
f(x ,y)ddd y 2(y)f(x ,y)d［.x Y－型］ c 1(y)
D
在积分中要正确选择积分次序与正确给出积分
限，且定积分中的各种技巧在这里仍然适用。
练习一：将二重积分化成二次积分 If(x,y)dxdy
D: 由四条直线 : x=3，x=5, y
sin ydxd y1dyysin ydx o
Dy
y 0 y2
x
1
0(siynysiny)dy
1si1n
二次积分中的第一次积分要易于计算， 且最终形成只是关于第二个变量的函数。
(练习)将二重积分化成二次积分 If(x,y)dxdy
一、 先对x积分
D
y
b
o
D
ax
b
a
I dya f(x,y)dx
2 先对 y 积分（从下到上）
y
1
xydxdy
dx
x
xydy
D
x
x
xdx ydy
x
1 1(x3 x5)dx 1
20
24
D
3 先对 x 积分（从左到右）
0
1x
xydxdy d y
D
二重积分的计算法(1)
二、小结
二重积分在直角坐标下的计算公式
f ( x, y)d
b
dx
2 ( x) f ( x, y)dy.
［X型］
D
a
1( x)
f ( x, y)d
d
dy
2 ( y) f ( x, y)dx. ［Y型
D
c
1( y)
（在积分中要根据积分区域和被积 函数的特征正确选择积分次序）
练习题
一、 填空题:
例5 计算 yexydxdy, D : x 1, x 2, y 2, xy 1
D
22
解 D是X—型区域 I dx yexydy
要分部积分，不易计算
1
1 x
若先 x 后 y 则须分片
12
22
I dy yexydx dy yexydx
D
0
1 y
11
易见尽管须分片积分，但由于被积函
D
y 1( x)
两个交点.
a
b
a
b
其中函数1( x) 、2( x) 在区间 [a,b]上连续.
f ( x, y)d 的值等于以 D 为底，以曲面 z
D
f (x, y) 为曲顶的柱体的体积．
应用计算“平行截 面面积为已知的立
z
体求体积”的方法,
y
z f (x, y)
A(x0 )
y 2(x)
解 积分区域如图
原式
1 1 y
dy f ( x, y)dx .
00
y 1 x
例 3 改变积分
1
dx
2 x x2
f ( x, y)dy
2
dx
2x f ( x, y)dy的次序.
二重积分的计算
y x2
y2 2 1 2 x y 2 dy 2 y 1
1
y
xy d x
1 22 1
sin x d xd y, 其中D 是直线 例3. 计算 D x 所围成的闭区域. y y x 解: 由被积函数可知, 先对 x 积分不行, D xπ 因此取D 为X - 型域 : π x O 0 y x D: 0 xπ π sin x x sin x d xd y dx d y 0 D x 0 x
二重积分极坐标表达式
【注意】极坐标系下的面积元素为
d d d
直角坐标系下的面积元素为
区别
d dxdy
24
2.二重积分化为二次积分的公式
（1）极点O在区域D的边界曲线之外时 区域特征如图
j1 ( )
j 2 ( )
,
D
j1 ( ) j 2 ( ).
及直线 例2. 计算 D x yd , 其中D 是抛物线 y 所围成的闭区域. 2 y2 x 解: 为计算简便, 先对 x 后对 y 积分, y 则
y2 x y 2 D: 1 y 2
O 1
D
4 x
x yd d y
D
2
y2
2
a
a j1 ( x)
f (x, y)dy]dx .
j1 ( x0 )
j2 ( x0 )
V A(x)dx [
a
b
b j 2 ( x)
a j1 ( x)
f (x, y)dy]dx .
二重积分的计算 设f(x, y)0, D{(x, y)|j1(x)yj2(x), axb}. 对于x0[a, b], 曲顶柱体在xx0的截面面积为
第二节二重积分的计算法(1)
o
A
（2）的特例
d
0
2
( )
0
f ( cos , sin ) d .
3. 极坐标系下区域的面积
dd .
D
8
机动 目录 上页 下页 返回 结束
［观察练习］ 下列各图中区域 D 分别与 x , y 轴相切 于原点,试问 的变化范围是什么? (1)
i i
i
D
( ri ) 2 i 是比ri i更 高阶的无穷小量，若 1 略去 ( ri ) 2 i , 则得 2
o
i
A
i ri ri i ,
2
机动 目录 上页 下页 返回 结束
从而得极坐标系下的面积元素为
d rdrd
d
2 ( )
1 ( )
f ( cos , sin ) d .
6
机动 目录 上页 下页 返回 结束
（2）极点O恰在区域D的边界曲线之上时
( )
区域特征如图
,
0 ( ).
o
D
（1）的特例
A
f ( cos , sin ) dd D
6
2 sin r
4 sin
r d r 15 ( 3 ) 2
13
机动 目录 上页 下页 返回 结束
sin( x 2 y 2 ) dxdy, 【例 4】计算二重积分 2 2 x y D 2 2 其中积分区域为 D {( x , y ) | 1 x y 4}.
o
a x
a
arccos
a
第二节： 二重积分的计算(一)
D { ( x, y ) | c y d , 1( y) x 2( y) }
y
y
d
·M 1
x 1( y ) D
c
·M 2
x 2( y )
d
x 1( y )
x 2( y )
D
c
· M 1
·M 2
0
x
0
x
特点：用平行于 x 轴的直线自左往右穿过 D 时，与 D 的边界最多只有两个交点。
D : 0 x 1, x2 y x,
y x2
( x2 y)dxdy
1 dx
0
x
x
2
(
x
2
y)dy
D
1
[
x
2
(
x x2 ) 1 ( x x4 )]dx 33 .
0
2
140
例3：计算二重积分 x y d x d y
D
其中 D 是由抛物线 y 2 x 及直线
所围成的闭区域。
b a
d
x
2(x) 1(x)
f (x,
y) d y
累次积分法又俗称 “穿线法”
0
ax
bx
X 型区域
y
• 若 D 是一边平行于坐标轴的
d
矩形区域，如图所示，则
D
c
f (x, y) d x d y
0a
bx
D
b a
d
x
d c
f (x,
y) d y
d c
d
y
b
a
f (x,
y) d x
• 当 D 既是 X 型，又是 Y 型区域时
D
(0,1)为顶点的三角形.
第二节 二重积分的计算
其中 D由 y =
y
1
y=x
y= x
x , y = x所围 .
解 (按先 y后 x积分次序计算 )
I = ∫ dx ∫
0 1
1
x
x
sin y dy y
o
1
x
积不出的积分，无法计算。 积不出的积分，无法计算。
(改变积分次序 , 按先 x后 y积分次序计算 )
sin y 1 sin y I = ∫ dy ∫ 2 dx = ( y − y 2 )dy 0 y ∫0 y y
积分域由两部分组成: 解: 积分域由两部分组成
0 ≤ y ≤ 2x − x2 D1 : , 0≤ x ≤1
0 ≤ y ≤ 2 − x D2 : 1≤ x ≤ 2
y = 2− x
视为 型区域 将D = D + D2 视为Y–型区域 , 则 1
1− 1− y2 ≤ x ≤ 2 − y D: , 0≤ y ≤1
∫∫D
b a d
f (x, y) dx dy
ϕ2 ( x)
1
= ∫ d x ∫ (x) f (x, y) dy ϕ = ∫ d y∫
c
ψ 2 ( y)
ψ 1( y) y)
f (x, y) dx
y y = ϕ (x) 2 d x =ψ2 ( y) x =ψ1( y) D y y = ϕ1(x) c o a x bx
根据二重积分的几何意义, 根据二重积分的几何意义,当
D
时,
为底， ∫∫ f ( x, y )dσ 等于以 D 为底，以曲面 z = f ( x, y ) 为顶的 曲顶柱体的体积． 曲顶柱体的体积．
z 应用计算“ 应用计算“平行截 面面积为已知的立 y = ϕ2 (x) 体求体积”的方法, 体求体积”的方法
y
1
y=x
y= x
x , y = x所围 .
解 (按先 y后 x积分次序计算 )
I = ∫ dx ∫
0 1
1
x
x
sin y dy y
o
1
x
积不出的积分，无法计算。 积不出的积分，无法计算。
(改变积分次序 , 按先 x后 y积分次序计算 )
sin y 1 sin y I = ∫ dy ∫ 2 dx = ( y − y 2 )dy 0 y ∫0 y y
积分域由两部分组成: 解: 积分域由两部分组成
0 ≤ y ≤ 2x − x2 D1 : , 0≤ x ≤1
0 ≤ y ≤ 2 − x D2 : 1≤ x ≤ 2
y = 2− x
视为 型区域 将D = D + D2 视为Y–型区域 , 则 1
1− 1− y2 ≤ x ≤ 2 − y D: , 0≤ y ≤1
∫∫D
b a d
f (x, y) dx dy
ϕ2 ( x)
1
= ∫ d x ∫ (x) f (x, y) dy ϕ = ∫ d y∫
c
ψ 2 ( y)
ψ 1( y) y)
f (x, y) dx
y y = ϕ (x) 2 d x =ψ2 ( y) x =ψ1( y) D y y = ϕ1(x) c o a x bx
根据二重积分的几何意义, 根据二重积分的几何意义,当
D
时,
为底， ∫∫ f ( x, y )dσ 等于以 D 为底，以曲面 z = f ( x, y ) 为顶的 曲顶柱体的体积． 曲顶柱体的体积．
z 应用计算“ 应用计算“平行截 面面积为已知的立 y = ϕ2 (x) 体求体积”的方法, 体求体积”的方法
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 2
D1
1 y x
o
2 x2 2 2x dx 2 dy 1 dx x 2 dy y y 1 1 2 2 1 x
1 1 2
2
x
81 192
例4 改换二次积分 0 dx 0 f ( x , y )dy 的积分次序. 解： D：0≤y ≤ x, 0 ≤ x ≤ 1
1
x
y
1
1( x)
b
x x+dx b
x
z=f (x, y)
A( x)
D
f ( x , y )dy
A( x)
1(x)
y
f ( x , y )d
a [
b
b
2(x)
2 ( x )
1( x)
f ( x , y )dy]dx
a dx
2 ( x )
1( x)
f ( x , y )dy
y
D1
o
D2 D3
x
D
.
D1 D2 D3
x2 例3 计算 2 d , D y
其中D由y =2, y=x及xy=1所围闭区域
2 x2 2 yx y 2 d 1 dy 1 y 2 dx D y
解: D为Y－型区域
y 2 1 o • •
1 x y
3 6 1
o
y=x2 1x
1x x 1 2 3 6 0 12
2. Y－型积分区域D： 1(y)≤x≤2(y) , c ≤y≤d
x=1( y) y d y d y d
x=2( y)
D
x=1( y)
x=2( y)
x=1( y)
D
D
c o
x
c o
x
d
c o
f ( x , y )d c [ ( y ) f ( x , y )dx ]dy
D
1
2 ( y)
c dy
d
2 ( y)
1( y)
f ( x , y )dx
x=2( y) x
f ( x , y )d c dy
d
D
2 ( y)
1(
y)
f ( x , y )dx
D是Y 型区域，二重积分化为先对x，
后对y的二次积分。 关键：确定各积分变量的积分限。 后积分的先定限,先积分的后定限,限内作条线, 先交的为下限,后交的为上限。
D
y
2
x yd 0 dx 0
2 D
1
2 2 x
x ydy
2
y = 2 2 x o
1
y 0 x dx 2 0 1 1 0 (4 x 2 8 x 3 4 x 4 )dx 1 4 2x 2 3 5 0 15
0 dx 0 f ( x, y )dy
y=x D x
1
1
x
f ( x , y )dxdy
D
0
0 dy y f ( x , y )dx
1
1
例5 改换二次积分 0 dy 0
1
2 y y2
f ( x , y )dx 的积分次序.
解： D : 0 x
2 y y ,0 y 1
a
f ( x , y )d V a A( x )dx
D
b
x
b
x
一、 直角坐标系下的计算法.
1. X－型积分区域D: 特点： 穿过区域且平行于y轴的直线与区域边 界相交不多于两个交点.
1(x)≤y≤2(x) , a ≤x≤b
y o
y 2 ( x)
y
y 2 ( x)
例1’ 计算 xyd ,
D
其中D为y2 =x 和y =x2 所围的闭区域.
D也为Y－型区域 D 0 y 1, y 2 x y
y 1 x=y2
x y
xyd
D
0 dy y xydx
2
1
y
o
1 x
1 12
2 计算 x 例2 ydσ ,
其中D为由 x=0 和 y=0 及 y = 22x所围成闭域. 解: D为X－型区域
3
5 1
y
2
y x 1 2
D也为Y－型区 域
2 x yd 0 dy 0 D 2 1 y 2
x 2 ydx
o
1
x
1 15
X－型区域的特点： 穿过区域且平行于y轴的 直线与区域边界相交不多于两个交点. Y－型区域的特点：穿过区域且平行于x轴的 直线与区域边界相交不多于两个交点. 3. 若区域如图， 则必须分割. 在分割后的三个区域上分别 使用积分公式
第二节 二重积分的计算法
一、直角坐标系下的计算法 二、极坐标系下的计算法
基本思路：化为定积分
f ( x , y )d 的值等于以 D 为底，
D
以曲面 z f ( x , y ) 为曲顶柱体的体积．
z
z f ( x, y)
应用计算“平行截 面面积为已知的立 体求体积”的方法,
y
A( x )
f ( x , y )d a dx ( x ) f ( x , y )dy D
1
b
2 ( x )
D是X型区域，二重积分化为先对y，
后对x的二次积分。 关键：确定各积分变量的积分限。 后积分的先定限,先积分的后定限,限内作条线, 先交的为下限,后交的为上限。
例1 计算 xyd ,
y x o a
y 2 ( x) y 1 ( x)
D
D
D
a
y 1 ( x)
x o a b
y 1 ( x)
b
x b
z y
o
z a
z f ( x, y)
y 2 ( x) y 1 ( x)
f ( x , y )d
D
a A( x )dx
2 ( x )
x= y
1 x 1 2 dy y 3 1
2 3 y
y
1 2 1 1 ( y 5 )dy 3 y
x
1y 1 81 4 3 2 4 y 1 192
2
2
D也为X－型区域
若先对y再对x积分
x y 2 d D
y
2
x=y
D2
x2 x2 2 d 2 d D y D y
D
其中D为y2 =x 和y =x2 所围的闭区域.
解: D为X－型区域
D 0 x 1, x
1
2
y x
x
xyd 0 dx x xydy
2
D
y 1
y x
y 0 x dx 2 x
1 2
2
x
1 1 2 5 0 ( x x )dx 2
2
x 2 y y2 x 2 + ( y – 1 ) 2 = 1 y 1 1 x2 y 1 2 y y2 f ( x , y )dx 2 0 dy 0
D1
1 y x
o
2 x2 2 2x dx 2 dy 1 dx x 2 dy y y 1 1 2 2 1 x
1 1 2
2
x
81 192
例4 改换二次积分 0 dx 0 f ( x , y )dy 的积分次序. 解： D：0≤y ≤ x, 0 ≤ x ≤ 1
1
x
y
1
1( x)
b
x x+dx b
x
z=f (x, y)
A( x)
D
f ( x , y )dy
A( x)
1(x)
y
f ( x , y )d
a [
b
b
2(x)
2 ( x )
1( x)
f ( x , y )dy]dx
a dx
2 ( x )
1( x)
f ( x , y )dy
y
D1
o
D2 D3
x
D
.
D1 D2 D3
x2 例3 计算 2 d , D y
其中D由y =2, y=x及xy=1所围闭区域
2 x2 2 yx y 2 d 1 dy 1 y 2 dx D y
解: D为Y－型区域
y 2 1 o • •
1 x y
3 6 1
o
y=x2 1x
1x x 1 2 3 6 0 12
2. Y－型积分区域D： 1(y)≤x≤2(y) , c ≤y≤d
x=1( y) y d y d y d
x=2( y)
D
x=1( y)
x=2( y)
x=1( y)
D
D
c o
x
c o
x
d
c o
f ( x , y )d c [ ( y ) f ( x , y )dx ]dy
D
1
2 ( y)
c dy
d
2 ( y)
1( y)
f ( x , y )dx
x=2( y) x
f ( x , y )d c dy
d
D
2 ( y)
1(
y)
f ( x , y )dx
D是Y 型区域，二重积分化为先对x，
后对y的二次积分。 关键：确定各积分变量的积分限。 后积分的先定限,先积分的后定限,限内作条线, 先交的为下限,后交的为上限。
D
y
2
x yd 0 dx 0
2 D
1
2 2 x
x ydy
2
y = 2 2 x o
1
y 0 x dx 2 0 1 1 0 (4 x 2 8 x 3 4 x 4 )dx 1 4 2x 2 3 5 0 15
0 dx 0 f ( x, y )dy
y=x D x
1
1
x
f ( x , y )dxdy
D
0
0 dy y f ( x , y )dx
1
1
例5 改换二次积分 0 dy 0
1
2 y y2
f ( x , y )dx 的积分次序.
解： D : 0 x
2 y y ,0 y 1
a
f ( x , y )d V a A( x )dx
D
b
x
b
x
一、 直角坐标系下的计算法.
1. X－型积分区域D: 特点： 穿过区域且平行于y轴的直线与区域边 界相交不多于两个交点.
1(x)≤y≤2(x) , a ≤x≤b
y o
y 2 ( x)
y
y 2 ( x)
例1’ 计算 xyd ,
D
其中D为y2 =x 和y =x2 所围的闭区域.
D也为Y－型区域 D 0 y 1, y 2 x y
y 1 x=y2
x y
xyd
D
0 dy y xydx
2
1
y
o
1 x
1 12
2 计算 x 例2 ydσ ,
其中D为由 x=0 和 y=0 及 y = 22x所围成闭域. 解: D为X－型区域
3
5 1
y
2
y x 1 2
D也为Y－型区 域
2 x yd 0 dy 0 D 2 1 y 2
x 2 ydx
o
1
x
1 15
X－型区域的特点： 穿过区域且平行于y轴的 直线与区域边界相交不多于两个交点. Y－型区域的特点：穿过区域且平行于x轴的 直线与区域边界相交不多于两个交点. 3. 若区域如图， 则必须分割. 在分割后的三个区域上分别 使用积分公式
第二节 二重积分的计算法
一、直角坐标系下的计算法 二、极坐标系下的计算法
基本思路：化为定积分
f ( x , y )d 的值等于以 D 为底，
D
以曲面 z f ( x , y ) 为曲顶柱体的体积．
z
z f ( x, y)
应用计算“平行截 面面积为已知的立 体求体积”的方法,
y
A( x )
f ( x , y )d a dx ( x ) f ( x , y )dy D
1
b
2 ( x )
D是X型区域，二重积分化为先对y，
后对x的二次积分。 关键：确定各积分变量的积分限。 后积分的先定限,先积分的后定限,限内作条线, 先交的为下限,后交的为上限。
例1 计算 xyd ,
y x o a
y 2 ( x) y 1 ( x)
D
D
D
a
y 1 ( x)
x o a b
y 1 ( x)
b
x b
z y
o
z a
z f ( x, y)
y 2 ( x) y 1 ( x)
f ( x , y )d
D
a A( x )dx
2 ( x )
x= y
1 x 1 2 dy y 3 1
2 3 y
y
1 2 1 1 ( y 5 )dy 3 y
x
1y 1 81 4 3 2 4 y 1 192
2
2
D也为X－型区域
若先对y再对x积分
x y 2 d D
y
2
x=y
D2
x2 x2 2 d 2 d D y D y
D
其中D为y2 =x 和y =x2 所围的闭区域.
解: D为X－型区域
D 0 x 1, x
1
2
y x
x
xyd 0 dx x xydy
2
D
y 1
y x
y 0 x dx 2 x
1 2
2
x
1 1 2 5 0 ( x x )dx 2
2
x 2 y y2 x 2 + ( y – 1 ) 2 = 1 y 1 1 x2 y 1 2 y y2 f ( x , y )dx 2 0 dy 0