第四章 电路原理
(完整版)电路原理课后习题答案
因此, 时,电路的初始条件为
t〉0后,电路的方程为
设 的解为
式中 为方程的特解,满足
根据特征方程的根
可知,电路处于衰减震荡过程,,因此,对应齐次方程的通解为
式中 。由初始条件可得
解得
故电容电压
电流
7-29RC电路中电容C原未充电,所加 的波形如题7—29图所示,其中 , 。求电容电压 ,并把 :(1)用分段形式写出;(2)用一个表达式写出。
或为
第六章“储能元件”练习题
6—8求题6-8图所示电路中a、b端的等效电容与等效电感.
(a) (b)
题6—8图
6—9题6—9图中 , ; 。现已知 ,求:(1)等效电容C及 表达式;(2)分别求 与 ,并核对KVL。
题6-9图
解(1)等效电容
uC(0)=uC1(0)+uC2(0)=-10V
(2)
6—10题6-10图中 , ; , , ,求:(1)等效电感L及 的表达式;(2)分别求 与 ,并核对KCL。
应用规则2,有 ,代入以上方程中,整理得
故
又因为
当 时,
即电流 与负载电阻 无关,而知与电压 有关.
5—7求题5-7图所示电路的 和输入电压 、 之间的关系。
题5-7图
解:采用结点电压法分析。独立结点 和 的选取如图所示,列出结点电压方程,并注意到规则1,得(为分析方便,用电导表示电阻元件参数)
应用规则2 ,有 ,代入上式,解得 为
(f)理想电流源与外部电路无关,故i=—10×10—3A=—10—2A
1-5试求题1—5图中各电路中电压源、电流源及电阻的功率(须说明是吸收还是发出)。
(a) (b) (c)
题1-5图
解(a)由欧姆定律和基尔霍夫电压定律可知各元件的电压、电流如解1—5图(a)故电阻功率 (吸收20W)
电路原理课件_第4章_谐振互感三相 (1)

g g 1 IL U ( ) ( j 0C ) U I C j 0 L
g
g
电感电流与电容电流幅值相同,相位差180°
2)并联谐振品质因数
谐振时电路感纳(容 纳)与电导之比。
1 0 L R
IL C Q R 1 1 IR L U
R
1 U 0 L
R 当 Q 0 L
i2 u22
di2 U12 e12 M dt
3)同名端 二个线圈间绕向不同时,产生的互感电压方向不同。
1
di1 0 , 图1:当 i1 增加时 dt 线圈2互感电压方向为 2 2 。 di1 u2 M dt
di1 0, dt 线圈2互感电压方向为 2 2。
i1
2
u1
减小电阻或增大电感可使UL变大。电压放大。
对于电流源:采用并联谐振方法 。
IL R Q并 0 L I S
增大电阻或减小电感可使IL变大。电流放大。
4.2 互感耦合电路
1)互感现象 邻近线圈间由于磁通 的交链,一个线圈电流的 变化会在另一线圈产生感 应电势(互感电势),这 一现象为互感偶合。 线圈1中通以电流
dψ1 dL1i1 di1 L1 线圈1 的自感电势 e11 dt dt dt
用电压降表示 线圈2 的互感电势
di1 U11 e11 L1 dt
互感电压 参考方向
dψ21 dMi1 di1 e21 M dt dt dt
用电压降表示
i1 u11
u21
di1 U 21 e21 M dt
同理: 当 i 2 变化时,引起 的变化, 二个线圈中产生感应电势, 线圈2 的自感电势: 用电压降表示:
ch4讲稿-电路原理教程(第2版)-汪建-清华大学出版社

时,I1=3A,I2=7A。问当合上K,调节R3,使I2=5A时,I1=?
解 由电路中的线性关系I1=a+kI2 ,根据已知条件,有
2=a+6b
I1 R1
N
则解R2当之3I=I2,2a=得+57Aba时=,-4 , b=1
I1=-4+1*5=1A
R3 K
例 –US1 +
IS
N0
–+ US2
a
Uab=k1IS+k2US1+k3US2
4-2 叠加定理
4-2-222 备注 7、关于定理的应用
- 例2 已知i1=5A,i2=2A,
若将电阻R3沿虚线钳 断,求钳断后的i1。
i1 + R1 us
i1 + R1
- us
i3=0
R3
R2
R2
R3
- R1us+ i2
R3
R1
R2
R2
i2
R3
i1=i1+i1 i1=5–2=3A
i1 + R1
- us
3A
4-2 叠加定理
4-2-2 备注 9、电路中的线性关系(两支路的电压、电流为线性关系)
+ im
-um Rm
含源 线性 网络
in
+
y=kx+b
- Rn
un 先用替代定理,再用叠加定理
+ im
-um Rm
含源
+
- 线性 un
网络
um=um+um= um+a1un im=im+im= im+a2un
R3
R2
《电路原理》(第2版) 周守昌 目录

第九章 拉普拉斯变换
§9-1 拉普拉斯变换 §9-2 拉普拉斯变换的基本性质 §9-3 进行拉普拉斯反变换的部分分式展开法 §9-4 线性动态电路方程的拉普拉斯变换解法
第十章 电路的复频域分析
§10-1 基尔霍夫定律的复复频域导纳 §10-3 用复频域模型分析线路动态电路 §10-4 网络函数
绪论
第一章 基尔霍夫定律和电阻元件
§1-1 电路和电路模型 §1-2 电流和电压的参考方向 §1-3 基尔霍夫定律 §1-4 电阻元件 §1-5 独立源 §1-6 受控源 §1-7 运算放大器 §1-8 支路分析法
第二章 电阻电路的分析
§2-1 线性电路的性质·叠加定理 §2-2 替代定理 §2-3 戴维宁定理 §2-4 诺顿定理 §2-5 有伴电源的等效变换 §2-6 星形电阻网络与三角形电阻网络的等效变换 §2-7 特勒根定理 §2-8 互易定理 §2-9 节点分析法 §2-10 回路分析法 §2-11 电源的转移
第三章 动态元件和动态电路导论
§3-1 电容元件 §3-2 电感元件 §3-3 耦合电感元件 §3-4 单位阶跃函数和单位冲激函数 §3-5 动态电路的输入— 输出方程 §3-6 初始状态与初始条件 §3-7 零输入响应 §3-8 零状态响应 §3-9 全响应
第四章 一阶电路与二阶电路
§4-1 一阶电路的零输入响应 §4-2 一阶电路的阶跃响应 §4-3 一阶电路的冲激响应 §4-4 一阶电路对阶跃激励的全响应 §4-5 二阶电路的冲激响应 §4-6 卷积积分及零状态响应的卷积计算法
第一章基尔霍夫定律和电阻元件11电路和电路模型12电流和电压的参考方向13基尔霍夫定律14电阻元件15独立源16受控源17运算放大器18支路分析法第二章电阻电路的分析21线性电路的性质叠加定理22替代定理23戴维宁定理24诺顿定理25有伴电源的等效变换26星形电阻网络与三角形电阻网络的等效变换27特勒根定理28互易定理29节点分析法210回路分析法211电源的转移第三章动态元件和动态电路导论31电容元件32电感元件33耦合电感元件34单位阶跃函数和单位冲激函数35动态电路的输入输出方程36初始状态与初始条件37零输入响应38零状态响应39全响应第四章一阶电路与二阶电路41一阶电路的零输入响应42一阶电路的阶跃响应43一阶电路的冲激响应44一阶电路对阶跃激励的全响应45二阶电路的冲激响应46卷积积分及零状态响应的卷积计算法第五章正弦电流电路导论51正弦电压和电流的基本概念52线性电路对正弦激励的响应正弦稳态响应53正弦量的相量表示法54基尔霍夫定律的相量形式55电路元件方程的相量形式56阻抗和导纳57阻抗的串联与并联第六章正弦电流电路的分析61正弦电流电路的相量分析62正弦电流电路中的功率63谐振电路64含有耦合电感元件的正弦电流电路65理想变量器第七章三相电路71对称三相电压72三相制的联接法73对称三相电路的计算74不对称三相电路的计算75三相电路中的功率第八章非正弦周期电流电路的分析81周期函数的傅里叶级数展开式82线性电路对周期性激励的稳态响应83非正弦周期电流和电压的有效值平均功率84傅里叶级数的指数形式85周期信号的频谱简介86对称三相电路中的高次谐波第九章拉普拉斯变换91拉普拉斯变换92拉普拉斯变换的基本性质93进行拉普拉斯反变换的部分分式展开法94线性动态电路方程的拉普拉斯变换解法第十章电路的复频域分析101基尔霍夫定律的复频域形式102电路元件的复频域模型复频域阻抗和复频域导纳103用复频域模型分析线路动态电路104网络函数附录非线性电路1非线性电阻元件及其约束关系2非线性电阻元件的串联和并联3非线性电阻电路的图解分析法4小信号分析法绪论返回
电路分析第四章

A
u
2 3
2 3i
8 9
v
-
0.5A
+
14 3
V
2 3
V
+
+
1V -
a
i
a
+
-
1V + 10 i1 2 N1 4 0.5A
a i1 1/3A b 图(c) 2 4 1/6A
图(d)
(3) 为求i1,将N2用1/3A电流源替代(图(c) 、(d))
4.1 叠加定理 (Superposition Theorem)
一、线性电路的齐次性和叠加性 线性电路:由线性元件和独立源构成的电路。 1.齐次性(homogeneity)(又称比例性,proportionality) 齐次性:若输入x(t) → 响应y(t) ,则输入K x(t) → Ky(t)
+ x(t) -
电 路
+ y(t) -来自+ Kx(t) -
+
电路
Ky(t) -
2.叠加性(superposition)
若输入x1(t) → y1(t)(单独作用) ,
x2(t) → y2(t) … xn(t) → yn(t) 则x1(t) 、x2(t) … xn(t) 同时作用时 响应y (t)= y1(t)+ y2(t)+ … +yn(t) + x1(t) -
3.替代后外电路及参数不能改变(只在一点等效)。
4. 3 互易定理 (Reciprocity Theorem)
例:
a
Us + 对(a): 对(b):
《电路原理导论》第四章习题解答
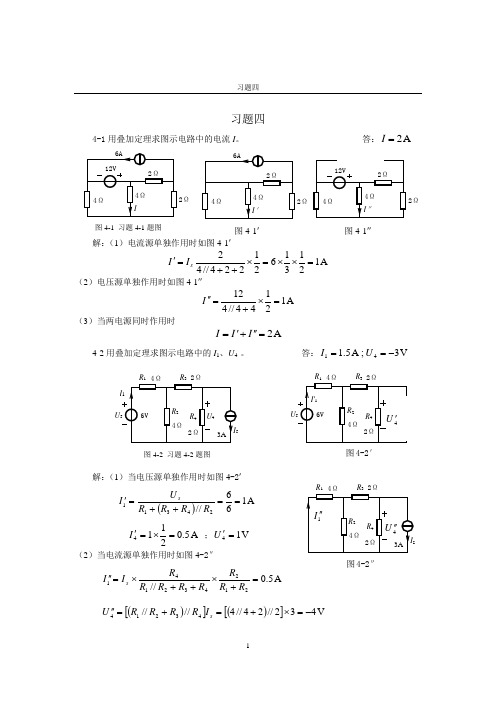
习题四习题四4-1用叠加定理求图示电路中的电流I 。
答:A 2=I解:(1)电流源单独作用时如图4-1′A 12131621224//42=⨯⨯=⨯++='sI I(2)电压源单独作用时如图4-1″A 12144//412=⨯+=''I(3)当两电源同时作用时A 2=''+'=I I I4-2用叠加定理求图示电路中的I 1、U 4 。
答:V 3;A 5.141-==U I解:(1)当电压源单独作用时如图4-2′()A 166//24311==++='R R R R U I sA 5.02114=⨯='I ;V 14='U (2)当电流源单独作用时如图4-2″A 5.0//212432141=+⨯++⨯=''R R R R R R R R I I s()[]()[]V 432//24//4////43214-=⨯+=+=''s I R R R R U 图4-1 习题4-1题图图4-2 习题4-2题图2Ω图4-1′ 2Ω图4-1″图4-2′图4-2″习题四(3)当两电源同时作用时A 5.15.01111=+=''+'=I I I V 341444-=-=''+'=U U U 4-3利用叠加定理求图4-3电路中的电压U 。
答:V 6=U解:(1)当电压源单独作用时如图4-3′V 11516=+⋅='U (2)当电流源单独作用时如图4-3″A 51556=+⨯=''I ,V 551=⨯=''U (3)当两电源同时作用时V 651=+=''+'=U U U4-4利用叠加定理求图示电路的电压U ab 。
答:V 9=ab U解:(1)当电流源单独作用时如图4-4′V 5.46241866186A 3-=⨯-=Ω⨯+⨯-='abU (2)当电压源单独作用时如图4-4″A 875.12.1936181218121236==+⨯+=''us I习题四V 5.1312875.15312181218=⨯⨯=Ω⨯''+=''usabI U (3)当两电源同时作用时V 95.135.4=+-=''+'=ab abab U U U 4-5图4-5电路中已知Ω=11R ,Ω=22R ,Ω=33RΩ=44R ,Ω=55R ,V 6=s U ,A 7=s I ,试用叠加定理求电路中的I 。
第四章_电路原理图绘制提高

2、设置输入输出端口 定义端口名称 设定端口外形 设定端口类形 设定端口名的位置 设定端口宽度 设定端口坐标 设定端口边线颜色 设定端口填充颜色 文字标注颜色 是否选取
2、设置输入输出端口
不定义端口类型 定义端口为输出类型 定义端口为输入类型 定义端口为双向类型
4.1 使用绘制电路工具
4.1.8 放置电路方块图 1、Place/Sheet Symbol 或单击 执行命令后,光标变为十字状,在方 块图的一角单击鼠标,再将鼠标移到 方块图的另一角,再单击鼠标。 2、设置电路方块图 在放置状态下,按Tab;或放置完后用 鼠标双击端口,可打开Sheet Symbol对 话框。
元件库默的元 件型号 元件的流水号
显示在图纸上 的元件型号
元件的封装类 型
4、元器件属性对话框 Part
元件库默的元件型号 元件的封装类型 元件的流水号 显示在图纸上的元件型号 定义图纸元件的路径 定义子元件序号 切换选取状态 显示元器件的隐藏引脚 显示元器件标注 显示元器件标注栏的栏名
4、元器件属性对话框 Part
2、设置文本框属性 在放置状态下,按Tab;或放完后用鼠标双 击该文本框,可打开Text Frame对话框
4.2 图形绘制
4.2.7 绘制直角矩形 1、Place/Drawing Tools/Rectangle 或单击 2、设置直角矩形属性 在放置状态下,按Tab; 或放完后用鼠标双击该 矩形,可打开 Rectangle对话框
4.1 使用绘制电路工具
4.1.1 画导线 1、Place/Wire 或单击工具栏中的 2、画导线的步骤 3、导线属性对话框的设置
4.1 使用绘制电路工具
4.1.1 画导线 1、Place/Wire 或单击工具栏中的 2、画导线的步骤 3、导线属性对话框的设置
模电课件第四章集成运算放大电路

§4.1集成运算放大电路概述 一、集成运放的电路结构特点
集成运算放大电路:高电压放大倍数的直接耦合多级放大电路。
2019/7/28
模电课件
二、集成运放的电路组成
1、输入级:运算放大器的输入级通常是差分放大电路,其主 要功能是抑制共模干扰和温漂,双极型运放中差分管通常采 用CC-CB复合管,以便拓展通频带。 2、中间级:电压放大,要求:放大倍数要尽可能大,通常采 用共201射9/7/2或8 共源电路,并采用恒模电流课源件 负载和复合管以增加电压 放大倍数。
工作在放大状态。
当T0与 T1特性参数完全一致时,由U BE0 = U BE1可推得
IB0 = IB1 = IB IC0 = IC1 = Io 由基极输入回路得,
Io
IR
VCC
U BE R
I0 2IB
I0
2
I0
所以,I0
1 1 2
IR
基准电流
输出电流
当
时,I0 IR 。
在集成运放电路中通常只能制作小容量(几十pF)电容,不能 制作大201容9/7/量28 电解电容,级间通常模采电课用件 直接耦合。
四、以电流源为有源负载的放大电路
在集成运放的共射(共源)放大电路中,为了提高电压放大 倍数,常用电流源电路取代Rc (或Rd ),这样在电源电压不 变的情况下,既获得合适的静态电流,又可以得到很大的等效 的Rc(或 Rd )。
(1) 运放电路的结构分解 输入级是一个差动放大电路,主要由T1、T3(共集-共基组合)
和T2、T4组成。中间放大级由T16、T17、T13组成共集—共射电路; 输出级由T14、T18 、 T19组成互补输出电路。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
R11i1 R12i2 R21i1 R22i2 RM 1i1 RM 2i2
R1M iM u s11 R2 M iM u s 22 RMM iM usMM
usjj
us 0
当电源us出现在回路j中 否则
, j 1, 2,
u2 us ris
例 4.1-4 图 4.1-5 为 一线性有源二端网络 A , 其内部结构不详。已知激 励源 us 是下列数值时的实 验数据为: 当us=10V,i=1A; 当 us=20V , i=1.5A 。 问当us=30 V时,电流i=?
+ -
us
线性有源二 端网络A
i
图 4.1-5
i) (m i 1 N
R21 RM 1
(i ) usMM
当一独立源作用时,其他独立源应设为零(独 立理想电压源短路,独立理想电流源开路)。 若电路中含有受控源,叠加时受控源不要单 独作用,在独立源每次单独作用时受控源都 要保留其中,其数值随每一独立源单独作用 时控制量数值的变化而变化。 叠加方式是任意的,可一次使一个独立源单 独作用,也可一次使几个独立源同时作用。
△I
(f)
电路中某支路电阻值由R→R+△R变化时,电路中各部分 的电压、电流变化由线性无源二端网络P与R+△R及△E 35 连接的电路(图 4.2-8(f))确定。
例4.2-3 如图4.2-7所示电路,已知 E=2V,R1=R2=400Ω,R3=R4=R5=800Ω, 问当R1变为500Ω时,求I5。
I (a)
线性有 源二端 网络A R
替 图 4.2-8 I (b) 代 I=I’ (c) 线性有 -△R 定 线性有 - △E= 源二端 源二端 理 网络A R 网络A + I△ R
△R
R+△R
即可得到:
线性有 源二端 网络A 线性 有源 二端 R+△R (d) 网络A
I+△I
I
R
+
(e)
线性 + △E= 无源 I△ R 二端 R+△R 网络P
例4.3-1 图4.3-6所示电路,负载电阻 RL 可以改变。求 RL=1Ω 其上的电流 i ; 若RL改变为6Ω,再求电流i。
图 4.3-6
例4.3-2 对图4.3-7所示电路,求电压u。
图 4.3-7
例4.3-3 对图4.3-8所示电路,求负载
RL上消耗的功率pL。 图4.3-8
例4.3-4 对图4.3-9所 示电路,已知:IR=2A, R I=1/3A; R增加10Ω时, IR=1.5A,I=1/2A; 求R减小10Ω时,I=?。
R1 8A + 8V – 13A R2
R1 3A + 3V – 5A R2
I
I'=1A +
2A RL
2V –
解: 采用倒推法:设I'=1A,推出此时us'=34V。
则
i us ' i' us us 51 即 i ' i' 1 1.5V us 34
入端电阻
Ki + 线性不含独 Ku 立源的二端 网络 -
+ us
线性有源二 端网络A
i
i ( g kf usf kf isf ) ( g kf usf kf isf ) gus
f f A
i0 gus (i0为常数)
第4章 电路的若干定理
4.2 替代定理
图 4.2-1 平衡电桥电路
替代定理
具有唯一解的电路中,若知某支路k的电压为 uk,电流为ik,且该支路与电路中其他支路无 耦合,则无论该支路是由什么元件组成的, 都可用下列任何一个元件去置换: (1)电压等于uk的理想电压源; (2) 电流等于ik的理想电流源; (3) 阻值为uk/ik的电阻。 若ik或uk只知其一,结论(1)和(2)依然成立。
l 1 i 1 (i ) sll i 1 l 1 (i ) sll i 1 M N N M N
(i ) u s11 i 1 N
N
R1M R2 M
R21
u
i 1 N
(i ) s 22
(i ) u sMM i 1 i) us(11 ) us(i22
RMM R1M R2 M RMM
例 4.2-2 如 图 4.2-5 所 示 电 路 , 已 知 uab=0,求电阻R。
图 4.2-5
补偿定理*
电路中,任何一电阻 的电阻值变动将导致 整个电路各支路电流 重新分配,补偿定理 描绘了线性电路电阻 变化量和各支路电流 变化量的关系 。图 4.2-6
线性有 源二端 网络A I R
33
的二端电路N,对其两个端子来说可等 效为一个理想电压源串联内阻的模型。 其理想电压源的数值为有源二端电路N 的两个端子间的开路电压uoc,串联的内 阻为N内部所有独立源置零(理想电压源 短路,理想电流源开路),受控源保留时 两端子间的等效电阻Req,常记为R0 。
图4.3-1 戴维南定理示意图
i +
(1) 开路、短路法。
uoc R0 isc
(2) 外加电源法。
u Req R0 i
42
图4.3-3 求等效内阻的两种方法的电路
4.3.2 诺顿定理
一个含独立电源、线性受控源和线性电
阻的二端电路N,对两个端子来说可等 效为一个理想电流源并联内阻的模型。 其理想电流源的数值为有源二端电路N 的两个端子短路时其上的电流isc,并联 的内阻等于N内部所有独立源为零时电 路两端子间的等效电阻,记为R0。
我们也可以由替代定理结 合叠加定理去更好地理解电路的基本 分析方法,如节点电压法:
Gk1v1 Gk 2v2
节点 k + vk Gkk
Gknvn uskf Gkf iskk
f
其它节点 节点 k
-Gkf
节点 f
+ vf -
例 4.2-1 对图4.2-4所示电路,求电流i1。
图 4.2-4
第4章 电路的若干定理
4.1 叠加定理 4.2 替代定理 4.3 戴维南定理和诺顿定理 4.4 特勒根定理 4.5 互易定理 4.6 对偶电路与对偶原理
电路定理反映了电路的一些基本性质,利 用这些性质有利于我们更好更清晰地理解 电路,以及理解我们处理电路的一些基本 分析和计算方法。 利用电路定理有助于我们简化和计算电路 ,甚至于一些不完整的电路在给出一定的 数据后仍然可以利用电路定理分析求解。
u -
+ i u
-
u uoc R0i
i +
有源二 端网络N + 有源二 端网络N
u
-
替代定理
u -
i
图4.3-2 证明戴维南定理用图
+ 有源二 端网络N uoc -
+
无源二 端网络 -iR0 N0 -
+
i
叠 加 定 理
开路电压uoc的计算可以直接断开二个端子进行; 等效内阻R0的求取通常采用下面两种方法:
usjj (i )
(i ) us ; 0
usjj usjj (i ) , j 1, 2,
i 1
N
,M
m im
?
i
(i ) m
i) (m
R11 R11 m R21 RM 1 us11 us 22 usMM R1M R2 M RMM RM 1 R11 ( u ) lm u lm
无源一端口网络:网络内部不含有独立电源。
第4章 电路的若干定理
4.1 叠加定理
叠加定理可表述为:在任何由线
性元件、线性受控源及独立源组 成的线性电路中,每一支路的响 应(电压或电流)都可以看成是各 个独立电源单独作用时,在该支 路中产生响应的代数和。
给每个独立电源编号(1--N),则原电路和第i 个独立电源us (i)单独作用时电路的回路电流 的KVL方程为:
i
a A 1. 几个名词 (1) 端口( port )
i
b
端口指电路引出的一对端钮,其中从一个端钮(如a) 流入的电流一定等于从另一端钮(如b)流出的电流。
(2) 一端口网络 (network) (亦称二端网络) 网络与外部电路只有一对端钮(或一个端口)联接。 (3) 含源(active)与无源(passive)一端口网络 含源一端口网络: 网络内部含有独立电源。
例4.1-1 如图4.1-2所示电路,求电压uab和 电流i1。
图 4.1-2
例4.1-2 如图4.1-3电路,含有一受 控源,求电流i, 电压u。
图4.1-3
4.1.2 齐次定理(线性定理)
齐次定理:当仅有一个激
励源(独立电压源或独立电 流源)作用于线性电路,其 任意支路的响应(电压或电 流)与该激励源成正比。
线性有 源二端 网络A
I + △I R+△R
线性有 源二端 网络A
(a)
I+△I R+△R
线性有 源二端 网络A
I+△I + △E R+△R
△E +
(b) 由叠加定理
线性有 △E 源二端 + R + △ R 网络A
34 (c)
I'
+
图 4.2-7
线性无 源二端 网络P R+△R
(d)
I”
+ -
△E
R2 R5 I5 R4 36
R1 I1
R3
E +
图 4.2-7
