高程系统
高程系统的概念

高程系统:概念、历史与发展高程系统是测量学中的一个概念,用于确定地球表面点的高程位置。
高程系统的发展经历了不同的历史阶段,从早期的参考椭球体到现代的大地水准面,都在不断地完善和改进。
本文将详细介绍高程系统的概念,包括参考椭球体、大地水准面、高程起算点、高程测量方法、高程系统应用、高程系统的历史与发展等方面。
1.参考椭球体参考椭球体是高程系统的基础之一,它是一个虚构的椭球体,用于模拟地球的形状。
84椭球体是当前广泛使用的一种参考椭球体,其半长轴为6378137米,扁率(长短轴之比)为298.257224。
参考椭球体的形状和大小是由两个主轴和扁率确定的,这些参数是通过测量地球表面的点位数据计算得出的。
2.大地水准面大地水准面是指与平均海水面重合并延伸到大陆内部的水平面。
大地水准面是一个理想的等高面,用于表示地球表面的海拔高程。
大地水准面的形状和大小与地球的形状和大小密切相关,因为它的形成是由地球表面的重力场和海水面共同作用的结果。
3.高程起算点高程起算点是高程系统的起点,通常是以某一点的高程作为基准,然后通过测量得出其他点的高程。
在中国的传统测量中,黄海海平面被广泛采用作为高程起算点。
随着测量技术的发展,现代高程起算点通常采用全球定位系统(GPS)测量的水准点。
4.高程测量方法高程测量方法包括水准测量、三角测量、GPS测量等方法。
水准测量是使用水准仪测量两点之间的高差,三角测量是通过测量三角形角度和边长来确定点位高程的方法,GPS测量则是通过接收卫星信号来确定点位高程的现代方法。
这些方法可以根据不同的需求和条件进行选择和应用。
5.高程系统应用高程系统广泛应用于水利、交通、建筑、地质等领域。
例如,在水利工程中,高程系统被用于确定水库大坝和河道的高程位置,以确保水利工程的稳定性和安全性;在交通工程中,高程系统被用于确定道路和桥梁的高程位置,以确保交通的顺畅和安全;在建筑领域中,高程系统被用于确定建筑物和公共设施的高程位置,以确保城市的规划和建设的美观和质量。
第四节我国的高程系统
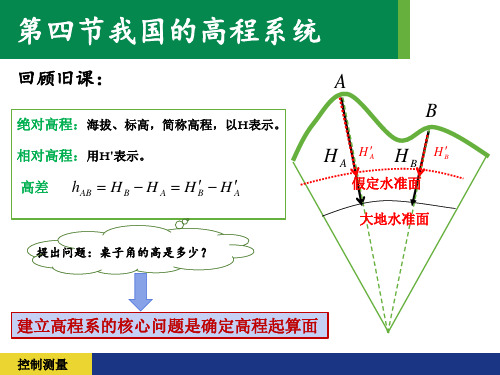
回顾旧课:
绝对高程:海拔、标高,简称高程,以H表示。 相对高程:用H′表示。
高差 hAB H B H A H B H A
提出问题:桌子角的高是多少?
A B
H H H A A
H B
B
假定水准面
大地水准面
建立高程系的核心问题是确定高程起算面
控制测量
第四节我国的高程系统
四、水准测量的理论闭合差
2、正常水准面不平行性对水准测量产生的影响 B
Hn
结论:沿两条不同路线施测的两点 间高差结果不一致。
控制测量
A h3
N
h/3H3
h2 h1
h/2 H2
h/1
H1
O
大地水准面
C
7
第四节我国的高程系统
四、水准测量的理论闭合差
3、水准测量理论闭合差
已知:闭合环形OABNO
控制测量
向量之间的夹角。
控制测量
第四节我国的高程系统
二、高程系统之间的关系
控制测量
第四节我国的高程系统
二、高程系统之间的关系
第四节我国的高程系统
控制测量
第四节我国的高程系统
三、我国的高程系统
❖ 我国现行的两个高程系统: ▪ 1956年黄海高程系的水准原点高72.2893米 ▪ 1985国家高程基准的水准原点高72.2604米
∵:
H
B 测
H 测 B
∴:即使水准测量完全没有误差,这个水准环形路线的闭 合差也不为零。
在闭合环形水准路线中,由于水准面不平行所产生的闭合 差称为理论闭合差。
措施:对高差结果加改正数,统一到“正常高高程系统”。
控制测量
高程系统简单介绍

高程系统简单介绍高程系统是指一种用来确定和测量地表和地球表面上各个点的高度的技术和方法。
高程系统在地理信息系统、土地测绘、工程设计等领域应用广泛,能够提供各种精度要求下的地表数据,为地质勘探、水文分析、地形建模等研究提供基础数据。
高程系统的原理是通过测量地球表面上的点相对于其中一基准面的高度差。
基准面可以是大地水准面、椭球面或其他参考面。
在实际应用中,通常采用水准测量或全球导航卫星系统(GNSS)测量等方法来确定点的高程。
高程系统可以提供绝对高程(相对于大地水准面)或相对高程(相对于参考点或其中一标高面)的测量结果。
高程系统包括高程控制网、高程测量和高程计算三个主要组成部分。
高程控制网是由一系列具有已知高度的基准点和控制点组成的测量网络,用于提供高程测量的参考框架。
高程测量是通过测量和记录各个点的高程差来确定点的高度。
高程计算是通过数学模型和计算方法,将测量结果转化为高程数值。
高程计算可以包括大地水准面的拟合计算,以及椭球面的转化计算等。
高程系统的应用范围广泛。
在土地测绘中,高程系统可以用来确定土地的坡度和坡向,以及地表特征的高程分布。
在工程设计和建设中,高程系统可以用来确定地面的高度和变化,以进行地形分析和土地利用评估。
在地质勘探和矿产资源调查中,高程系统可以用来确定地下水位和矿井的高程,以进行资源评估和开采规划。
在水文分析和环境研究中,高程系统可以用来确定河流、湖泊和水库的高程,以进行水文模拟和水资源管理。
高程系统的精度要求根据应用的需求而定。
在一般土地测绘和工程设计中,高程精度一般要求在几厘米到几十厘米范围内。
在水利工程和交通工程等需要更高精度的领域,高程精度要求可以达到亚厘米甚至毫米级。
为了满足不同应用的需要,高程系统通常会与其他测量技术和数据源相结合,如全球导航卫星系统、激光扫描和遥感影像等。
总之,高程系统是一种应用于地理信息系统、土地测绘和工程设计等领域的技术和方法,用于确定和测量地表和地球表面上各个点的高度。
不同高程系统之间的关系和转换

不同高程系统之间的关系和转换概述:不同高程系统是指在地球表面上测量和表示高程的不同方法和标准。
由于地球是一个不规则的椭球体,不同的高程系统会采用不同的基准和测量方法。
本文将介绍几种常见的高程系统,包括大地水准面、椭球面高程、正高程和大地水准面与椭球面的转换关系。
一、大地水准面(Mean Sea Level)大地水准面是指地球上所有点的平均海平面。
它是一个理想的参考面,用于测量和比较不同地点的高程。
在大地水准面上,海平面的高程被定义为0。
大地水准面可以通过水准测量和重力测量等方法来确定和维护。
二、椭球面高程(Ellipsoidal Height)椭球面高程是指相对于一个参考椭球体的高程。
参考椭球体是一个近似于地球形状的椭球体,可以通过测量和计算得到。
椭球面高程的基准点通常是一个参考椭球体上的某个点,称为基准点。
椭球面高程与大地水准面的高程之间存在一定的差异,这个差异被称为大地水准面偏差。
三、正高程(Orthometric Height)正高程是指相对于大地水准面的高程。
它是通过测量从地面到大地水准面的垂直距离来确定的。
正高程可以通过水准测量和重力测量等方法来测量和计算。
在测量正高程时,需要考虑地球表面的地形起伏和重力变化等因素。
四、大地水准面与椭球面的转换关系由于大地水准面和椭球面是两种不同的高程系统,它们之间存在一定的转换关系。
常见的转换方法有以下几种:1. 大地水准面高程到椭球面高程的转换:大地水准面高程可以通过加上大地水准面偏差来转换为椭球面高程。
大地水准面偏差可以通过水准测量和重力测量等方法来确定。
2. 椭球面高程到大地水准面高程的转换:椭球面高程可以通过减去大地水准面偏差来转换为大地水准面高程。
3. 正高程到椭球面高程的转换:正高程可以通过加上大地水准面偏差来转换为椭球面高程。
4. 椭球面高程到正高程的转换:椭球面高程可以通过减去大地水准面偏差来转换为正高程。
需要注意的是,大地水准面和椭球面的转换关系是基于特定的基准点和参考椭球体来确定的,不同的基准点和参考椭球体会导致不同的转换结果。
高程系统及其相互关系

高程控制 网的布设
高程测量
外业计算
内业计算
确定地面点正常高流程
Process of Getting Normal Height
往测高差=所有往测测站高差读数中数之和
往 h12
高程控制 网的布设
往测
高程测量
1
水 准 返测
… …
水
2
准
点
外业计算
点
测站
内业计算
返 h12
返测高差=所有返测测站高差读数中数之和
i i ζ i H 大 H常,( i 1, ,n ) ζ为似大地水准面差距
1
2
… n
4.3.不同高程系统之间的关系
二、GPS水准
Relation of different height system
i vi a0 a1 xi a2 yi a3 xi a4 xi yi a5 yi a6 xi a7 xi yi a8 xi yi a9 yi
p gdh (GPU )
1 GPU =1千伽米=105厘米2/秒2
4.2.高程系统
Height System
大地高 正 高
几何意义 物理意义 半物理意义 物理意义 物理意义
H正 H常
H力
1 gdh gm 1
正常高 力 高
m
1
gdh
gdh
45
重力位数
p gdh
(路线闭合差) W HA h中2 h中2 HB A1 12
外业计算
(路线闭合差改正)v i
即简单的平差
R
n 1
Ri
W
i
内业计算
高程系统

高程系统武汉大学测绘学院 潘正风一.正高系统正高系统以大地水准面为高程基准面,地面上任一点的正高是指该点沿垂线方向至大地水准面的距离。
⎰=gdh g H B m B 1正式中,B m g 为B 点沿垂线方向不同深处重力的平均值,⎰gdh 是过B 点的水准面与起始大地水准面之间位能差。
但由于B 点沿垂线方向不同深处的重力不能测定,所以B m g 不能精确得到,正高也就不能精确求得。
二.正常高系统将B m g 用正常重力B m γ代替,便得到另一种系统的高程,称其为正常高。
⎰=gdh H Bm B γ1常式中,g 由沿水准测量路线的重力测量得到,dh 是水准测量的高差,B m γ是按正常重力公式算得的正常重力平均值。
正常重力按下式计算:H 3086.00-=γγH 以米为单位,正常重力0γ按1975年国际地球物理和大地测量联合会推荐的正常重力公式计算:()ϕϕγ2sin 0000058.0sin 005302.01032.978220-+=我国规定采用正常高高程系统。
正常高以似大地水准面为基准面的高程。
在海面上, 大地水准面和似大地水准面重合。
三.国家高程基准采用大地水准面作为高程基准面。
有“1956年黄海高程系统”和“1985国家高程基准”。
m H H 029.05685-=四.GPS 高程GPS 除测出平面坐标外,还测出大地高H (即沿WGS-84椭球体法线到椭球面的距离)。
如果能知道WGS-84椭球面和似大地水准面之间的差值,则可由GPS 的大地高求得正常高。
在一个区域确定WGS-84椭球面和似大地水准面之间的差值,是在该区域建立高精度的似大地水准面。
通过高精度GPS 控制网和水准测量控制网,综合利用重力资料,进行似大地水准面的拟合来实现。
高程系统

正高系统正高系统以大地水准面为高程基准面,地面上任一点的正高是指该点沿垂线方向至大地水准面的距离。
要推算这种平均重力值,必须知道地面和大地水准面之间岩层的密度分布,这是不能用简单方法来推求的。
所以过去都是采用近似的数据,只能求得正高的近似值。
高程系统正常高系统1945年前苏联的M.C.莫洛坚斯基提出了“正常高”的概念,即将正高系统中的分母gm 改用平均正常重力值γm来代替,γm是可以精确计算的,因此正常高也可以精确地计算出来。
由各地面点沿正常重力线向下截取各点的正常高,所得到的点构成的曲面,称为似大地水准面,它是正常高的基准面。
似大地水准面很接近于大地水准面,在海洋上两者是重合的,在平原地区两者相差不过几厘米,在高山地区两者最多相差2米。
似大地水准面不是等位面,没有明确的物理意义。
它是由各地面点按公式计算的正常高来定义的,这是正常高系统的缺陷,其优点是可以精确计算,不必引入人为的假定。
中国《大地测量法式》规定采用正常高系统。
高程系统大地高程地面点在三维大地坐标系中的几何位置,是以大地经度、大地纬度和大地高程表示的。
大地高程以椭球面为基准面,是由地面点沿其法线到椭球面的距离。
大地高程可直接由卫星大地测量方法测定,也可由几何和物理大地测量相结合来测定。
采用前一种方法时,直接由卫星定位技术测定地面点在一全球地心坐标系中的大地高程;采用后一种方法时,大地高程分为两段来测定,其中由地面点至大地水准面或似大地水准面的一段由水准测量结果加上重力改正而得,由大地水准面或似大地水准面至椭球面的一段由物理大地测量方法求得。
当以大地水准面为过渡面时,则:H =Hg+N,式中N为大地水准面至椭球面的差距,称为大地水准面起伏。
如以似大地水准面为过渡面,则:H =H r+ζ,式中ζ为似大地水准面至椭球面的距离,称为高程异常。
由于正高Hg是由地面点沿垂线至大地水准面的距离, 而正常高H r 是由地面点沿正常重力线至似大地水准面的距离,所以由上述两种方法计算得出的大地高程有差异,差数约为十分之几毫米。
高程系统

选择合适的高程异常已知点
所谓已知点的高程异常值一般是通过水准测 量测定正常高、通过GPS测量测定大地高后获得 的。在实际工作中,一般采用在水准点上布设 GPS点或对GPS点进行水准联测的方法来实现,为 了获得好的拟合结果要求采用数量尽量多的已知 点,它们应均匀分布,并且最好能够将整个GPS 网包围起来。
高程异常已知点的数量
若要用零次多项式进行高程拟合时,要确定 1个参数,因此,需要1个以上的已知点;若要采 用一次多项式进行高程拟合,要确定3个参数, 需要3个以上的已知点;若要采用二次多项式进 行高程拟合,要确定6个参数,则需要6个以上的 已知点。
已知点为一个
把已知点上的高程异常改正到其 它点上去 定义了高程平差面,此平面沿着 直线方向前进 定义了高程平差面 二次曲面拟合定义了曲面
采用等值线图法确定点的正常高和正高时要 注意以下几个问题:
1、注意等值线图所适用的坐标系统,在求解正 常高或正高时,要采用相应坐标系统的大地高数据。 2、采用等值线图法确定正常高或正高,其结 果的精度在很大程度上取决于等值线图的精度。
2、地球模型法
地球模型法本质上 是一种数字化的等值 线图,目前国际上较 常采的地球模型有 EGM96、OSU91A等。带 入经纬度坐标即可得 到 ζ或hg 。不过可 惜的是这些模型均不 适合于我国。
GPS高程
高程系统
大地高系统
大地高系统是以参考椭球面为基准面的高程 系统。某点的大地高是该点到通过该点的参考椭 球的法线与参考椭球面的交点间的距离。大地高 也称为椭球高,大地高一般用符号H表示。 大地高是一个纯几何量,不具有物理意义, 同一个点,在不同的基准下,具有不同的大地高。
正高系统
正高系统是以大地水准面为基准面的高 程系统。某点的正高是该点到通过该点的铅 垂线与大地水准面的交点之间的距离,正高 用符号Hg表示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
黄河流域将统一使用“1985国家高程基准”
黄委水文局讯由于历史原因,黄河流域高程系统较为紊乱,目前使用的高程系统有9种之多(大沽、黄海、假定、冻结、1985国家高程基准、引据点III、导渭、坎门中潮值、大连葫芦岛),给流域规划、工程布局、工程设计、水文水情预报、河道冲淤变化、防汛指挥等工作带来诸多不便。
为了把已使用的高程基准换算到“1985国家高程基准”,需要制定统一的工作计划和技术标准,同时要把黄河流域未控区纳入“1985国家高程基准”,从而使黄河流域历史延用的各种高程和未控区统一到“1985国家高程基准”面。
“1985国家高程基准”是采用青岛验潮站1953年至1979年验潮资料计算确定的,1987年5月经国务院国测发[1987]198号文批准,依此基准推算全国各类水准点高程成果,逐步归算至“1985国家高程基准”。
黄河流域高程系统的统一,是由黄委统一管理,委设计院总负责,相关部门参与编制了《黄河流域统一高程系统任务书》,该任务书的编制为流域系统高程统一产生积极的影响。
黄委水文局作为高程系统主要使用单位和水文资料的收集提供部门,作了大量工作,提供了委属水文系统水文站、水位站、渠道站所使用的高程基面,并先后几次参加专家座谈、审查会。
统一高程系统是治黄重点项目的基础工作,是防汛工程建设、水资源开发利
用、水土保持生态环境建设工作的前提,是数字黄河、数字水文建设的服务平台,是保障《黄河近期重点治理开发规划》顺利实施的重要条件,高程系统的统一为全面推进“三条黄河”建设打下坚实的基础。
(水利部网站)。
