四面体外接球表面积公式
四面体外接球的球心、半径求法

四面体外接球的球心、在立体几何中,几何体外接球是一个常考的知识点,对于学生来说这是一个难点,一方面图形不会画,另一方面在画出图形的情况下无从下手,不知道球心在什么位置,半径是多少而无法解题。
本文章在给出图形的情况下解决球心位置、半径大小的问题。
、出现“墙角”结构利用补形知识,联系长方体。
【原理】:长方体中从一个顶点出发的三条棱长分别为a,b,c,则体对角线长为________ / 2 . b2 + ~2I = J a2+b2+C2,几何体的外接球直径2R为体对角线长I即R = ---------- --【例题】:在四面体ABCD中,共顶点的三条棱两两垂直, 其长度分别为1, V6,3,若该四面体的四个顶点在一个球面上,求这个球的表面积。
解:因为:长方体外接球的直径为长方体的体对角线长所以:四面体外接球的直径为AE的长即:4R2=AB2+AC2+AD2C 4R2 =12+32+ 府=16 所以R =2球的表面积为S=4;IR2=16;I二、出现两个垂直关系,利用直角三角形结论。
【原理】:直角三角形斜边中线等于斜边一半。
球心为直角三角形斜边中点。
【例题】:已知三棱锥的四个顶点都在球0的球面上,AB丄BC且PA =7,PB=5, PC =751,AC =10,求球0 的体积。
解:AB 丄BC 且PA =7,PB=5,P C=妬,AC =10,!_ 2因为=102所以知AC2=PA2+ PC2设球心坐标为O(x, y,z)贝U AO=BO=CO =DO ,由空间两点间距离公式知x 2 +y 2 +z 2 =(x -1)2 +(y -73)2 +z 2J 3解得 “1 y=- z =1所以PA 丄PC 所以可得图形为:在RtAABC 中斜边为AC 在RU PAC 中斜边为AC取斜边的中点0 , 在 RUABC 中 0A = 0B = 0C在 RtiPAC中 OP = OB =OC 所以在几何体中OP = OB =OC =OA ,即O 为该四面体的外接球的球心1R = — AC = 52 所以该外接球的体积为V 丄职―500工3 3 【总结】斜边一般为四面体中除了直角顶点以外的两个点连线。
球与几何体的切接问题

r3=392π3r3.故圆锥SD与其外接球的体积比为 3323ππrr33=392.故选A. 93
题型二 几何体的内切球
例3 (1)半径为R的球的外切圆柱(球与圆柱的侧面、两底面 都相切)的表面积为__6_π_R_2___,体积为__2_π_R_3___.
状元笔记
柱体的外接球问题,其解题关键在于确定球心在多面体中的 位置,找到球的半径或直径与多面体相关元素之间的关系,结合 原有多面体的特征求出球的半径,然后再利用球的表面积和体积 公式进行正确计算.常见的方法是将多面体还原到正方体或长方 体中再去求解.
思考题 1 (1)已知各顶点都在一个球面上的正四棱柱
(2)已知直三棱柱 ABC-A1B1C1 的 6 个顶点都在球 O 的球面 上,若 AB=3,AC=4,AB⊥AC,AA1=12,则球 O 半径为( C )
3 17 A. 2
B.2 10
C.123
D.3 10
【解析】 由球心 O 作平面 ABC 的垂线,设垂足为 BC 的中点 M.
又 AM=12BC=52,OM=12AA1=6,
【解析】 本题考查几何体的外接球的表面积.因为四个
面都是直角三角形,且AB⊥平面BCD,所以CD⊥BC或
CD⊥BD,不妨设CD⊥BC,由鳖臑ABCD的体积为
2 3
,得
1 3
S△
BCD·AB=
1 3
×
1 2
×1×BC×2=
2 3
,则BC=2,BD=
BC2+CD2
= 5.
将鳖臑ABCD补成直三棱柱如图,取BD的中点
∵球心 O 到四个顶点的距离相等,均等于该正三棱锥外接球 的半径 R,
立体几何专题:外接球问题中常见的8种模型(学生版)

立体几何专题:外接球问题中常见的8种模型1.知识梳理一、墙角模型适用范围:3组或3条棱两两垂直;可在长方体中画出该图且各顶点与长方体的顶点重合直接用公式(2R )2=a 2+b 2+c 2,即2R =a 2+b 2+c 2,求出R【补充】图1为阳马,图2和图4为鳖臑二、麻花模型适用范围:对棱相等相等的三棱锥对棱相等指四面体的三组对棱分别对应相等,且这三组对棱构成长方体的三组对面的对角线。
推导过程:三棱锥(即四面体)中,已知三组对棱分别相等,(AB =CD ,AD =BC ,AC =BD )第一步:画出一个长方体,标出三组互为异面直线的对棱;第二步:设出长方体的长宽高分别为a ,b ,c ,AD =BC =x ,AB =CD =y ,AC =BD =z ,列方程组,a 2+b 2=x 2b 2+c 2=y 2c 2+a 2=z 2⇒(2R )2=a 2+b 2+c 2=x 2+y 2+z 22,补充:V A −BCD =abc −16abc ×4=13abc 第三步:根据墙角模型,2R =a 2+b 2+c 2=x 2+y 2+z 22,R 2=x 2+y 2+z 28,R =x 2+y 2+z 28,求出R .三、垂面模型适用范围:有一条棱垂直于底面的棱锥。
推导过程:第一步:将ABC 画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O .第二步:O 1为ABC 的外心,所以OO 1⊥平面ABC ,算出小圆O 1的半径O 1D =r(三角形的外接圆直径算法:利用正弦定理a sin A =b sin B=csin C =2r ,OO 1=12PA .第三步:利用勾股定理求三棱锥的外接球半径:(1)(2R )2=PA 2+(2r )2⇔2R =PA 2+(2r )2;(2)R 2=r 2+OO 21⇔R =r 2+OO 21.公式:R 2=r 2+h 24四、切瓜模型适用范围:有两个平面互相垂直的棱锥推导过程:分别在两个互相垂直的平面上取外心O 1、O 2过两个外心做两个垂面的垂线,两条垂线的交点即为球心0,取B C 的中点为E ,连接OO 1、OO 2、O 2E 、O 1E 为矩形由勾股可得|OC |2=|O 2C |2+|OO 2|2=|O 2C |2+|O 1C |2-|CE |2∴R 2=r 21+r 22-l 24公式:R 2=r 21+r 22-l 24五、斗笠模型适用于:顶点的投影在底面的外心上的棱锥推导过程:取底面的外心01,连接顶点与外心,该线为空间几何体的高h ,在h 上取一点作为球心0,根据勾股定理R 2=(h -R )2+r 2⇔R =r 2+h 22h公式:R =r 2+h 22h六、矩形模型适用范围:两个直角三角形的斜边为同一边,则该边为球的直径推导过程:图中两个直角三角形ΔPAB 和ΔQAB ,其中∠APB =∠AQB =90°,求外接圆半径取斜边AB 的中点O ,连接OP ,OQ ,则OP =12AB =OA =OB =OQ 所以O 点即为球心,然后在ΔPOQ 中解出半径R 公式:R 2=l22(l 为斜边长度)七、折叠模型适用范围:两个全等三角形或等腰三角形拼在一起,或菱形折叠.推导过程:两个全等的三角形或者等腰拼在一起,或者菱形折叠,设折叠的二面角∠A EC =α,CE =A E =h .如图,作左图的二面角剖面图如右图:H 1和H 2分别为△BCD ,△A BD 外心,分别过这两个外心做这两个平面的垂线且垂线相交于球心O CH 1=r =BD 2sin ∠BCD,EH 1=h -r ,OH 1=(h -r )tanα2由勾股定理可得:R 2=OC 2=OH 21+CH 21=r 2+(h -r )2tan 2α2.公式:R 2=r 2+(h -r )2tan 2α2八、鳄鱼模型适用范围:所有二面角构成的棱锥,普通三棱锥方法:找两面外接圆圆心到交线的距离m ,n ,找二面角α,找面面交线长度l 推导过程:取二面角两平面的外心分别为O 1,O 2并过两外心作这两个面的垂线,两垂线相交于球心O ,取二面角两平面的交线中点为E ,则O ,O 1,E ,O 2四点共圆,由正弦定理得:OE =2r =O 1O 2sin α①在ΔO 1O 2E 中,由余弦定理得:O 1O 2 2=O 1E 2+O 2E 2-2O 1E O 2E cos α②由勾股定理得:OD 2=O 1O 2+O 1D 2③由①②③整理得:OD2=O 1O 2+O 1D 2=OE 2-O 1E 2+O 1D 2=O 1O 2sin α2-O 1E 2+O 1D 2=O 1E2+O 2E 2-2O 1E O 2E cos αsin 2α-O 1E 2+O 1D 2=O1E2+O2E2-2O1EO2Ecosαsin2α-O1E2+O1B2记O1E=m,O2E=n,AB=l,则R2=m2+n2-2mn cosαsin2α+l22公式:R2=m2+n2-2mn cosαsin2α+l222.常考题型3.题型精析题型一:墙角模型1(2023·高一单元测试)三棱锥A-BCD中,AD⊥平面BCD,DC⊥BD,2AD=BD=DC=2,则该三棱锥的外接球表面积为()A.3π2B.9π2C.9πD.36π1.(2022秋·陕西西安·高一统考期末)在《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑.已知在鳖臑A-BCD中,满足AB⊥平面BCD,且AB=BD=5,BC=3,CD=4,则此鳖臑外接球的表面积为()A.25πB.50πC.100πD.200π2.(2023·高一课时练习)《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年.在《九章算术》中,将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马.如图P-ABCD是阳马,PA⊥平面ABCD,PA=5,AB=3,BC=4.则该阳马的外接球的表面积为()A.1252π3B.50πC.100πD.500π33.(2023·广西南宁·统考二模)在《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,在鳖臑A -BCD 中,AB ⊥平面BCD ,CD ⊥AD ,AB =BD =2,已知动点E 从C 点出发,沿外表面经过棱AD 上一点到点B 的最短距离为10,则该棱锥的外接球的体积为.4.(2023春·辽宁朝阳·高二北票市高级中学校考阶段练习)已知四棱锥P -ABCD 的外接球O 的表面积为64π,PA ⊥平面ABCD ,且底面ABCD 为矩形,PA =4,设点M 在球O 的表面上运动,则四棱锥M -ABCD 体积的最大值为.题型二:麻花模型1(2023春·广东梅州·高二统考期中)已知三棱锥S -ABC 的四个顶点都在球O 的球面上,且SA =BC =2,SB =AC =7,SC =AB =5,则球O 的体积是()A.83π B.3223π C.423π D.823π1.(2022春·江西景德镇·高一景德镇一中校考期中)在△ABC 中,AB =AC =2,cos A =34,将△ABC 绕BC 旋转至△BCD 的位置,使得AD =2,如图所示,则三棱锥D -ABC 外接球的体积为.2.(2023秋·吉林·高一吉林一中校考阶段练习)如图,在△ABC 中,AB =25,BC =210,AC =213,D ,E ,F 分别为三边中点,将△BDE ,△ADF ,△CEF 分别沿DE ,EF ,DF 向上折起,使A ,B ,C 重合为点P ,则三棱锥P -DEF 的外接球表面积为()A.72π B.7143π C.14π D.56π3.(2023·江西·统考模拟预测)在三棱锥P -ABC 中,已知PA =BC =213,AC =BP =41,CP =AB =61,则三棱锥P -ABC 外接球的表面积为()A.77πB.64πC.108πD.72π4.(2022·全国·高三专题练习)已知四面体ABCD 的棱长满足AB =AC =BD =CD =2,BC =AD =1,现将四面体ABCD 放入一个轴截面为等边三角形的圆锥中,使得四面体ABCD 可以在圆锥中任意转动,则圆锥侧面积的最小值为.题型三:垂面模型1(2023·高一单元测试)在三棱锥P -ABC 中,PA ⊥平面ABC ,PA =6,BC =3,∠CAB =π6,则三棱锥P -ABC 的外接球半径为()A.3B.23C.32D.61.(2023·全国·高一专题练习)已知A ,B ,C ,D 在球O 的表面上,△ABC 为等边三角形且边长为3,AD ⊥平面ABC ,AD =2,则球O 的表面积为()A.4πB.8πC.16πD.32π2.(2020春·天津宁河·高一校考期末)在三棱锥P -ABC 中,AP =2,AB =3,PA ⊥面ABC ,且在△ABC 中,C =60°,则该三棱锥外接球的表面积为()A.20π3B.8πC.10πD.12π3.(2023·全国·高一专题练习)已知A ,B ,C ,D 在球O 的表面上,△ABC 为等边三角形且其面积为334,AD ⊥平面ABC ,AD =2,则球O 的表面积为()A.πB.2πC.4πD.8π4.(2022春·山东聊城·高一山东聊城一中校考阶段练习)在四棱锥P -ABCD 中,PA ⊥平面ABCD ,四边形ABCD 为矩形,BC =2,PC 与平面PAB 所成的角为30o ,则该四棱锥外接球的体积为()A.433π B.43πC.823πD.833π题型四:切瓜模型1(2023·贵州贵阳·校联考模拟预测)在三棱锥A -BCD 中,已知AC ⊥BC ,AC =BC =2,AD =BD =6,且平面ABD ⊥平面ABC ,则三棱锥A -BCD 的外接球表面积为()A.8πB.9πC.10πD.12π1.(2023·四川达州·统考二模)三棱锥A -BCD 的所有顶点都在球O 的表面上,平面ABD ⊥平面BCD ,AB =AD =6,AB ⊥AD ,∠BDC =2∠DBC =60°,则球O 的体积为()A.43πB.32π3C.49π3D.323π2.(2023春·陕西西安·高一长安一中校考期中)在直三棱柱ABC -A 1B 1C 1中,AB ⊥BC ,AB =BC =AA 1=4,点P 为B 1C 1的中点,则四面体PABC 的外接球的体积为()A..41416π B.41413π C.41412π D.4141π3.(2022·高一单元测试)四棱锥P -ABCD 的顶点都在球O 的表面上,△PAD 是等边三角形,底面ABCD 是矩形,平面PAD ⊥平面ABCD ,若AB =2,BC =3,则球O 的表面积为()A.12πB.16πC.20πD.32π4.(2021·高一课时练习)在四棱锥P -ABCD 中,平面PAD ⊥平面ABCD ,且ABCD 为矩形,∠DPA =π2,AD =23,AB =2,PA =PD ,则四棱锥P -ABCD 的外接球的体积为()A.163π B.323π C.643π D.16π5.(2023春·全国·高一专题练习)在四棱锥P-ABCD中,ABCD是边长为2的正方形,AP=PD=10,平面PAD⊥平面ABCD,则四棱锥P-ABCD外接球的表面积为()A.4πB.8πC.136π9D.68π3题型五:斗笠模型1(2023·全国·高一专题练习)正四面体S-ABC内接于一个半径为R的球,则该正四面体的棱长与这个球的半径的比值为()A.64B.33C.263D.31.(2022·高一专题练习)已知正四棱锥P-ABCD(底面四边形ABCD是正方形,顶点P在底面的射影是底面的中心)的各顶点都在同一球面上,底面正方形的边长为10,若该正四棱锥的体积为50 3,则此球的体积为()A.18πB.86πC.36πD.323π2.(2022·全国·高一专题练习)某四棱锥的底面为正方形,顶点在底面的射影为正方形中心,该四棱锥内有一个半径为1的球,则该四棱锥的表面积最小值是()A.16B.8C.32D.243.(2022春·安徽·高三校联考阶段练习)在三棱锥P-ABC中,侧棱PA=PB=PC=10,∠BAC=π4,BC=22,则此三棱锥外接球的表面积为.题型六:矩形模型1(2022春·全国·高一期末)已知三棱锥A-BCD中,CD=22,BC=AC=BD=AD=2,则此几何体外接球的表面积为()A.2π3B.2π C.82π3D.8π1.(2022春·广东惠州·高一校考期中)在矩形ABCD中,AB=6,BC=8,现将△ABC沿对角线AC翻折,得到四面体DABC,则该四面体外接球的体积为()A.1963π B.10003π C.4003π D.5003π2.(2022春·河北沧州·高一校考阶段练习)矩形ABCD中,AB=4,BC=3,沿AC将三角形ABC折起,得到的四面体A-BCD的体积的最大时,则此四面体外接球的表面积值为()A.25πB.30πC.36πD.100π3.(2022春·四川成都·高一统考期末)在矩形ABCD 中,AB =6,AD =8,将△ABC 沿对角线AC 折起,则三棱锥B -ACD 的外接球的表面积为()A.36πB.64πC.100πD.与二面角B -AC -D 的大小有关题型七:折叠模型1(2022春·陕西西安·高一长安一中校考期末)已知菱形ABCD 的边长为3,∠ABC =60°,沿对角线AC 折成一个四面体,使平面ACD 垂直平面ABC ,则经过这个四面体所有顶点的球的体积为().A.5152π B.6πC.515πD.12π1.已知等边△ABC 的边长为2,将其沿边AB 旋转到如图所示的位置,且二面角C -AB -C 为60°,则三棱锥C -ABC 外接球的半径为2.(2023·广西南宁·统考二模)蹴鞠,又名“蹴球”“蹴圈”等,“蹴”有用脚蹴、踢的含义,鞠最早系外包皮革、内饰米糠的球,因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动,类似今日的足球,现已知某“鞠”的表面上有四个点A ,B ,C ,D 满足AB =BC =CD =DA =DB =433cm ,AC =23cm ,则该“鞠”的表面积为cm 2.3.(2022秋·福建泉州·高三校考开学考试)在三棱锥S -ABC 中,SA =SB =AC =BC =2,SC =1,二面角S -AB -C 的大小为60°,则三棱锥S -ABC 的外接球的表面积为.4.(2022秋·山东德州·高二统考期中)已知在三棱锥中,S -ABC 中,BA ⊥BC ,BA =BC =2,SA =SC =22,二面角B -AC -S 的大小为5π6,则三棱锥S -ABC 的外接球的表面积为()A.56π3B.58π3C.105π4D.124π9题型八:鳄鱼模型1(2022春·四川成都·高一树德中学校考期末)已知在三棱锥S-ABC中,AB⊥BC,AB=BC=2,SA =SC=22,二面角B-AC-S的大小为2π3,则三棱锥S-ABC的外接球的表面积为()A.124π9B.105π4C.105π9D.104π91.(2023春·全国·高一专题练习)如图,在三棱锥P-ABC,△PAC是以AC为斜边的等腰直角三角形,且CB=22,AB=AC=6,二面角P-AC-B的大小为120°,则三棱锥P-ABC的外接球表面积为()A.5103π B.10π C.9π D.4+23π2.(2023·陕西榆林·统考三模)在三棱锥A-BCD中,AB⊥BC,BC⊥CD,CD=2AB=2BC= 4,二面角A-BC-D为60°,则三棱锥A-BCD外接球的表面积为()A.16πB.24πC.18πD.20π3.(2023春·安徽阜阳·高三阜阳市第二中学校考阶段练习)如图1,四边形ABCD中,AB=AD =2,CB=CD=2,AB⊥AD,将△ABD沿BD翻折至△PBD,使二面角P-BD-C的正切值等于2,如图2,四面体PBCD的四个顶点都在同一个球面上,则该球的表面积为()A.4πB.6πC.8πD.9π4.(2023·江西南昌·校联考模拟预测)在平面四边形ABCD中,AD=CD=3,∠ADC=∠ACB =90°,∠ABC=60°,现将△ADC沿着AC折起,得到三棱锥D-ABC,若二面角D-AC-B的平面角为135°,则三棱锥D-ABC的外接球表面积为.5.(2023春·广东广州·高三统考阶段练习)在三棱锥P-ABC中,△ABC为等腰直角三角形,AB=AC=2,△PAC为正三角形,且二面角P-AC-B的平面角为π6,则三棱锥P-ABC的外接球表面积为.。
专题06 经典三类球:外接球、内切球、棱切球(解析版)

专题06 经典三类球:外接球、内切球、棱切球【考点预测】考点一:正方体、长方体外接球1.正方体的外接球的球心为其体对角线的中点,半径为体对角线长的一半. 2.长方体的外接球的球心为其体对角线的中点,半径为体对角线长的一半. 3.补成长方体(1)若三棱锥的三条侧棱两两互相垂直,则可将其放入某个长方体内,如图1所示. (2)若三棱锥的四个面均是直角三角形,则此时可构造长方体,如图2所示. (3)正四面体P ABC -可以补形为正方体且正方体的棱长2a =,如图3所示.(4)若三棱锥的对棱两两相等,则可将其放入某个长方体内,如图4所示图1 图2 图3 图4考点二:正四面体外接球如图,设正四面体ABCD 的的棱长为a ,将其放入正方体中,2,显然正四面体和正方体有相同的外接球.正方体外接球半径为236R ==,即正四面体外接球半径为6R =.考点三:对棱相等的三棱锥外接球四面体ABCD 中,AB CD m ==,AC BD n ==,AD BC t ==,这种四面体叫做对棱相等四面体,可以通过构造长方体来解决这类问题.如图,设长方体的长、宽、高分别为,,a b c ,则222222222b c m a c n a b t ⎧+=⎪+=⎨⎪+=⎩,三式相加可得222a b c ++=222,2m n t ++而显然四面体和长方体有相同的外接球,设外接球半径为R ,则22224a b c R +=+,所以2228m n t R ++=.考点四:直棱柱外接球如图1,图2,图3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)图1 图2 图3第一步:确定球心O 的位置,1O 是ABC ∆的外心,则1OO ⊥平面ABC ; 第二步:算出小圆1O 的半径1AO r =,111122OO AA h ==(1AA h =也是圆柱的高); 第三步:勾股定理:22211OA O A O O =+⇒222()2hR r =+⇒22()2h R r =+R考点五:直棱锥外接球如图,PA ⊥平面ABC ,求外接球半径.图3-1C 1B 1AEFA 1O 1OO 2BC图3-2C 1B 1AA 1O 1OO 2BC图3-3C 1B 1AEFA 1O 1O O 2BC解题步骤:第一步:将ABC ∆画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ;第二步:1O 为ABC ∆的外心,所以1OO ⊥平面ABC ,算出小圆1O 的半径1O D r =(三角形的外接圆直径算法:利用正弦定理,得2sin sin sin a b c r A B C ===),112OO PA =; 第三步:利用勾股定理求三棱锥的外接球半径:①222(2)(2)R PA r =+⇔222(2)R PA r +②2221R r OO =+⇔221R r OO =+ 考点六:正棱锥外接球正棱锥外接球半径:222r h R h+= .考点七:垂面模型如图1所示为四面体-P ABC ,已知平面⊥PAB 平面ABC ,其外接球问题的步骤如下: (1)找出PAB △和ABC △的外接圆圆心,分别记为1O 和2O .(2)分别过1O 和2O 作平面PAB 和平面ABC 的垂线,其交点为球心,记为O . (3)过1O 作AB 的垂线,垂足记为D ,连接2O D ,则⊥2O D AB .(4)在四棱锥-12A DO OO 中,AD 垂直于平面12DO OO ,如图2所示,底面四边形12DO OO 的四个顶点共圆且OD 为该圆的直径.ADPO 1OCBhl rDB图1 图2考点八:锥体内切球方法:等体积法,即3VRS=体积表面积考点九:棱切球方法:找切点,找球心,构造直角三角形【典型例题】例1.(2022·河北邢台·高一阶段练习)已知菱形ABCD的边长为360BAD∠=︒,将△ABD沿BD折起,使A,C两点的距离为3A-BCD的外接球的表面积为()A.12πB.18πC.24πD.30π【答案】B【解析】【分析】确定折起后三棱锥A-BCD为正四面体,将此正四面体放置在正方体中,使得正方体的面对角线是正四面体的棱,正方体的对角线就是外接球的直径,此球也是三棱锥A-BCD的外接球.由此计算可得球表面积.【详解】由已知得BAD为等边三角形,∴对角线23BD AB BC CD DA=====将ABD△沿BD折起,使A,C两点的距离为3∴折起后三棱锥A-BCD为正四面体,各棱长都是23将此正四面体放置在正方体中,使得正方体的面对角线是正四面体的棱,设正方体的棱长为a23a=32a R =,其中R 为正方体的外接球半径,322R =, 由于正方体的外接球就是正四面体ABCD 的外接球, ∴正四面体ABCD 的外接球表面积为2418R ππ= 故选:B.例2.(2022·安徽·合肥市第六中学高一期中)设直三棱柱111ABC A B C -的所有顶点都在一个球面上,1AB AC AA ==,120BAC ∠=︒,且底面ABC 的面积为23接球的表面积是( ) A .16π B 4010πC .40πD .64π【答案】C 【解析】 【分析】由三角形面积公式求得AB ,由正弦定理求得底面三角形外接圆半径,设,M N 分别是ABC 和111A B C △的外接圆圆心,则MN 的中点O 是三棱柱111ABC A B C -的外接球球心,求球半径后可得表面积. 【详解】设1AB AC AA m ===,因为120BAC ∠=︒, 所以1sin120232m m ⨯⨯⨯︒=22m = 而30ACB ∠=︒,所以22sin 30r =︒(r 于是是ABC 外接圆的半径),22r =即22AM = 如图,设,M N 分别是ABC 和111A B C △的外接圆圆心,由直棱柱的性质知MN 的中点O 是三棱柱111ABC A B C -的外接球球心, 111222OM MN AA === 所以外接球为22R OA AM OM =+=()()2222210+=.于是球的表面积为24S R =π=(241040ππ=.故选:C.例3.(2022·湖南·长郡中学高一期中)如图,在正四棱台1111ABCD A B C D -中,4AB =,112A B =,若半径为r 的球O 与该正四棱台的各个面均相切,该球的表面积S =( )A .4πB .6πC .8πD .10π【答案】C 【解析】 【分析】作正棱台的轴截面.设内切球的半径为r ,利用勾股定理得到222MG FG MF +=,解得2r =.【详解】如图,作该正棱台的轴截面.其中E ,F ,M ,N 分别是AB ,CD ,11C D ,11A B 的中点,H ,K 是MN ,EF 的中点,G 是内切球的球心,H ,K 是内切球和上、下底面的切点,Q 是内切球和侧面11CDD C 的切点,内切球的半径为r ,由正棱台的结构可以得到,1HM =,2KF =,HG KG QG r ===,易得1MQ HM ==,2FQ FK ==,3MF =,2221MG r =+,2222FG r =+,且90MGF ∠=︒,所以222MG FG MF +=,即22149r r +++=,解得2r =248S r ππ==.故选:C.例4.(2022·河北省唐县第一中学高一期中)已知三棱锥P ABC -的各顶点都在同一球面上,且P A ⊥ 平面ABC ,AB AC ⊥,且1AB AC ==,若此球的表面程等于4π,则三棱锥P ABC -的体积为( )A 2B .1C 2D .13【答案】A 【解析】 【分析】将三棱锥P ABC -补成长方体,则三棱锥P ABC -的外接球即为该长方体的外接球,求出球的半径,即可得出长方体的对角线的长度,从而可得出答案. 【详解】由题意,将三棱锥P ABC -补成长方体,则三棱锥P ABC -的外接球即为该长方体的外接球.则该长方体的外接球的直径为该长方体的对角线. 如图,4S π=球,则球半径1R =, 所以()222222PA AB AC R PA ++=⇒=, 所以123P ABC ABC V S PA -∆=⋅=故选:A.例5.(2022·河南·高一期中)已知三棱锥P ABC -的四个顶点在球O 的球面上,3,4,5,5,34,PA PB PC AB AC ===== 41BC =O 的表面积为( )A .16πB .25πC .32πD .50π【答案】D 【解析】 【分析】利用勾股定理可证明三条侧棱,,PA PB PC 两两垂直,符合墙角模型,补成长方体,那么球的直径就是长方体的体对角线. 【详解】根据题中数据,22222+3534PA PC AC =+==,故PA PC ⊥,类似的,同理容易验证222+PA PB AB =,222+PC PB BC =,于是PA PB ⊥,PB PC ⊥, 即三条侧棱,,PA PB PC 两两垂直,下以P 为顶点,,,PA PB PC 分别为一个长方体的长宽高,将三棱锥P ABC -补成长方体, 易知长方体的外接球就是三棱锥P ABC -的外接球, 长方体的体对角线长为: 22234552++=于是球O 的表面积为(2250ππ⋅=.故选:D.例6.(2022·全国·3顶点的多面体为正八面体,那么该正八面体的内切球表面积为( )A .6πB .πC .43π D .4π【答案】B 【解析】 【分析】6正八面体的内切球半径,即可求出球的表面积. 【详解】2233622⎛⎫⎛⎫+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭如图,在正八面体中连接AF ,DB ,CE ,可得AF ,DB ,CE 互相垂直平分,在Rt AOD △中,22226262223AO AD OD ⨯=-=⨯⎪⎛⎫⎛⎫-= ⎪ ⎪ ⎪⎝⎭⎝⎭ 则该正八面体的体积1363236V =⨯= 该八面体的表面积236833S ==⎝⎭设正八面体的内切球半径为r ,13S r V =,即13333r ⨯=12r =, 24球S πr π∴==故选:B例7.(2022·山西·大同市第二中学校高一期中)球O 为三棱锥P ABC -的外接球,ABC 和PBC 都是边长为3PBC ⊥平面ABC ,则球的表面积为( ) A .28π B .20πC .18πD .16π【答案】B 【解析】 【分析】取BC 中点为T ,以及ABC 的外心为1O ,PBC 的外心为2O ,依据平面PBC ⊥平面ABC 可知12OO TO 为正方形,然后计算外接球半径,最后根据球表面积公式计算. 【详解】设BC 中点为T ,ABC 的外心为1O ,PBC 的外心为2O , 如图由ABC 和PBC 均为边长为3 则ABC 和PBC 23260=,又因为平面PBC ⊥平面ABC , 所以2O T ⊥平面ABC ,可知21O T O T ⊥ 且21O T O T =,过21,O O 分别作平面PBC 、平面ABC 的垂线相交于O 点O 即为三棱锥P ABC -的外接球的球心, 且四边形12OO TO ()22231-=的正方形,所以外接球半径2222145R OO O P =++则球的表面积为20π, 故选:B .例8.(2022·全国·高一单元测试)四个半径为2的球刚好装进一个正四面体容器内,此时正四面体各面与球相切,则这个正四面体外接球的表面积为( ) A .(168486)π+ B .(168426)π+ C .(188486)π+ D .(168326)π+【答案】A 【解析】 【分析】画出直观图,梳理条件,再画出截面图,从中找到等量关系,求出外接球半径,从而求出外接球的表面积. 【详解】如图1所示,正四面体ABCD 中,AH ⊥底面BCD ,E 、F 、G 、K 为四个球的球心,M 为CD 中点,连接BM ,AM ,易知B 、H 、M 三点共线,直线AH 交平面EFG 于点1H ,连接1EH ,交GF 于点N ,则N 为GF 的中点,因为内切球半径为2,故EF =4,画出截面ABM 如图2所示,正四棱锥EFGK 外接球球心设为O ,则正四面体ABCD 的外接球球心与正四面体EFGK 外接球球心重合,设正四面体ABCD 的外接球半径为R ,正四面体EFGK 外接球半径为r ,在图2中,EK =4,23EN =12433EH EN ==,146KH ==146OH r = 由22211OE OH EH =+,即2224643r r ⎫=+⎪⎪⎝⎭⎝⎭,解得:6r =所以1466OH r =-=过点E 作EP ⊥BM 于点P ,则EP =2 则△BEP ∽△1OEH∴1OH OE BE EP=6632= 解得:6BE =∴66R OB BE OE ==+=+∴正四面体ABCD 的外接球表面积(24168483S R ππ==+故选:A 【点睛】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.(多选题)例9.(2022·湖北·沙市中学高一期中)如图,已知棱长为1的正方体1111ABCD A B C D -中,下列命题正确的是( )A 3B .点P 在线段AB 上运动,则四面体111P A BC -的体积不变 C .与所有122πD .M 是正方体的内切球的球面上任意一点,则AM 32-【答案】BC 【解析】 【分析】对于A ,利用正方体的性质即得,对于B ,判断出四面体111P A B C -的高为1,底面积不变即得,对于C .先求出球的半径2R =,即可求体积,对于D .判断出线段AM 长度的最小值是A 到球心的距离减去内切球的半径,直接求解即可. 【详解】对于A ,由正方体的性质可知正方体外接球的直径为其体对角线,故正方体外接球的半径3A 错误; 对于B ,点P 在线段AB 上运动,则四面体111P A BC -的高为1,底面积不变,则体积不变,故B 正确;对于C ,与所有12条棱都相切的球的直径2R 等于面的对角线12BC 22R =2R =, 则球的体积334422(33V R ππ==⨯⨯=,故C 正确;对于D ,正方体的内切球为正方体的中心,内切球的半径为r , 可知线段AM 长度的最小值是A 到球心的距离减去内切球的半径, 正方体1111ABCD A B C D -的棱长为1,∴12r =,A 3AM 31-D 错误. 故选:BC .例10.(2022·广东·广州市协和中学高一期中)在三棱锥P ABC -中,33,5AB AC BC PA PB PC ======,D 、E 、F 分别为AB 、AC 、BC 的中点,则以下结论正确的是( )A .平面PDE ⊥平面ABCB .平面PAF ⊥平面ABCC .//AB 平面PEFD .三棱锥P ABC -的外接球表面积为625π16【答案】BCD 【解析】 【分析】对于A ,利用逆推方式要证明面面垂直,就去证明线面垂直,再去证线线垂直,根据题意不存在AM PM ⊥即可判断;对于B ,根据面面垂直的判定定理及等腰三角形的三线合一即可判断; 对于C ,根据线面平行的判定定理结合三角形的中位线定理即可判断;对于D ,要求三棱锥P ABC -外接球的表面积,首先找出外接球的球心,在利用球的半径、截面圆半径、球心到截面圆圆心的距离三者关系求出球的半径,再利用球的表面积公式即可判断; 【详解】对于A ,设AF 与DE 的交点为M ,则AF DE ⊥,若平面PDE ⊥平面ABC ,那么根据面面垂直的性质定理,必有AF ⊥平面PDE ,此时须有AM PM ⊥成立,又因为M 是AF 的中点,此时须有PA PF =成立,上式显然不成立,故A 不正确;对于B ,由于,AB AC PB PC ==,F 为BC 的中点,所以AF BC ⊥,PF BC ⊥,AFPF F =,故BC ⊥平面PAF ,而BC ⊂平面ABC ,所以平面PAF ⊥平面ABC ,故B正确;对于C ,由E , F 分别为AC ,BC 的中点,得//EF AB ,EF ⊂平面PEF ,AB ⊄平面PEF ,所以因此//AB 平面PEF ,故C 正确; 对于D ,作PN平面ABC 垂足为N ,则N 为正三角形ABC 的重心,所以22333,534,AN PN ===-设三棱锥P ABC -的外接球球心为O ,则O 在PN 上,连接AO ,设三棱锥P ABC -的外接球半径为R ,则在AON 中,()22243R R =-+,解得258R =,因此其外接球表面积为2625π4π16R =,故D 正确.故选:BCD.【点睛】解决此类型题的关系记住线面,面面平行与垂直的判定定理及性质定理,求外接球的问题关键核心就是找出球心,找球心的方法就是找截面圆的圆心,再做过截面圆的圆心的垂线,球心就在过截面圆的圆心的垂线上,然后球的半径、截面圆半径、球心到截面圆圆心的距离三者关系求出球的半径进而可以求解关于球的任何问题.【过关测试】 一、单选题1.(2022·广东·海珠外国语实验中学高一期中)已知一个圆锥的母线长为2,侧面积为2π.若圆锥内部有一个球,当球的半径最大时,球的体积为( ) A .3π B 23C 3D 43【答案】D 【解析】 【分析】由题可知球内切于圆锥,利用图形关系求得球的半径,即可得解. 【详解】由题可知,母线2PA PB ==,若内部有一个球,半径最大时, 球内切于圆锥,如图所示,O 为球心,M 为球O 与母线PB 的切点,E 为底面圆心, 设球O 的半径为R ,底面圆E 的半径为r 因为圆锥侧面积为2π,所以()1222π⋅=πr PB ,解得1==r EB . 由勾股定理222413=-=-=PE PB EB ,所以3PE = 又因为POM 与PBE △相似,31-=⇒=PO OM R R PB EB ,解得3R =, 所以球的体积344334333=π==V R . 故选:D2.(2022·天津市求真高级中学高一阶段练习)正方体的外接球与内切球的表面积之比是( ) A .13B .3C .33D 3【答案】B 【解析】 【分析】设正方体的棱长为a ,求出其外接球的半径和内切球的半径,再根据表面积公式可得结果. 【详解】设正方体的棱长为a 3,内切球的半径为12a ,所以正方体的外接球与内切球的表面积之比是2234142a ππ⎫⋅⎪⎝⎭⎛⎫⋅ ⎪⎝⎭3=. 故选:B3.(2022·云南师大附中高一期中)如图,蹴鞠,又名“蹋鞠”、“蹴球”、“蹴圆”、“筑球”、“踢圆”等,“跳”有用脚蹴、蹋、踢的含义,“鞠”最早系皮革外包、内实米糠的球.因而“蹴鞠”就是指古人以脚蹴、蹋、踢皮球的活动,类似今日的足球.2006年5月20日,蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家级非物质文化遗产名录.若将“鞠”的表面视为光滑的球面,已知某“鞠”表面上的四个点A ,B ,C ,D 满足13AB CD ==,5BD AC ==cm ,5AD BC ==cm ,则该“鞠”的表面积为( )A .20πcm 2B .24πcm 2C .27πcm 2D .29πcm 2【答案】D 【解析】 【分析】由于,,AB CD BD AC AD BC ===,所以可以把,,,A B C D 四点放到长方体的四个顶点上,则该长方体的体对角线就是“鞠”的直径,求出体对角线长,从而可求出该“鞠”的表面积 【详解】因为“鞠”表面上的四个点A ,B ,C ,D 满足13AB CD ==,25BD AC ==,5AD BC ==cm ,所以可以把,,,A B C D 四点放到长方体的四个顶点上,则该长方体的体对角线就是“鞠”的直径,设该长方体的长、宽、高分别为,,x y z ,“鞠”的半径为R ,则 2222(2)R x y z =++,由题意得22222220,13,25x y x z y z +=+=+=, 所以2222(2)29R x y z =++=,即2429R =, 所以该“鞠”的表面积为22429cm R ππ=, 故选:D4.(2022·浙江·嘉兴一中高一期中)在三棱锥P ABC -中,P A 、AB 、AC 两两垂直,3AP =,6BC =,则三棱锥外接球的表面积为( )A .57πB .63πC .45πD .84π【答案】C 【解析】 【分析】由P A ,AB ,AC 两两垂直,可判定该三棱锥为长方体的一部分,则三棱锥的外接球即为长方体的外接球,可知外接球半径为长方体体对角线的一半,进而求解. 【详解】由于P A ,AB ,AC 两两垂直,故可得该三棱锥为长方体的一部分, 因为外接球半径为长方体体对角线的一半, 所以2222235PA AB AC PA BC R +++==, 故2445S R ππ==, 故选:C5.(2022·安徽·合肥市第八中学高一期中)如图,在正四棱柱1111ABCD A B C D -中,底面ABCD 是边长为1的正方形,P 为11A D 上一点,且满足2APD π∠=,PA PD =,则以四棱锥P ABCD -外接球的球心O 为球心且与平面PBC 相切的球的体积为( )A 5πB 5πC 45πD 45π【答案】B 【解析】 【分析】在直角PAD △中,求得2PA PD ==O 即为四棱锥P ABCD -的外接球的球心,分别连接,,PN NQ PQ ,过点O 作OM PQ ⊥,证得OM ⊥平面PNQ ,求得25OM =25r =.【详解】在直角PAD △中,1AD =,PA PD =,可得222PA PD AD +=, 即2PA PB ==过正方形ABCD 的中心O 作1OO ⊥平面ABCD , 取AD 的中点N ,连接ON ,则ON ⊥平面PAD , 则直线1OO ON O =,则O 即为四棱锥P ABCD -的外接球的球心,分别连接,,PN NQ PQ ,在PNQ 中,过点O 作OM PQ ⊥, 又由BC ⊥平面PNQ ,可得OM BC ⊥, 因为BCPQ Q =,所以OM ⊥平面PBC ,又由PNQ 和QOM 相似,可得OM OQPN PQ =,所以1122525OQ PN OM PQ ⨯⋅==,所以O 为球心且与平面PBC 相切的球的半径为25r OM ==所以该球的体积为33445(3325V r πππ==⨯= 故选:B.6.(2022·安徽·淮南第一中学高一阶段练习)在三棱锥P ABC -中,,2,4,5PB AC PA PB AB AC BC ⊥=====,则三棱锥P ABC -外接球的表面积是( )A .52πB .643πC .1123πD .2563π【答案】B 【解析】 【分析】利用勾股定理证得AB AC ⊥,再根据线面垂直的判定定理可得AC ⊥平面PAB ,故三棱锥C PAB -的外接球在过底面PAB △外接圆圆心且垂直于底面PAB △的直线上,利用正弦定理求得PAB △外接圆的半径为r ,再根据三棱锥C PAB -外接球的半径为R 求出外接球半径,即可得出答案. 【详解】解:由2,4,5AB AC BC ===, 可得222BC AB AC =+,所以AB AC ⊥, 又,PB AC AB PB B ⊥⋂=,且PB ,AB 平面PAB ,所以AC ⊥平面PAB ,故三棱锥B PAB -的外接球在过底面PAB △外接圆圆心且垂直于底面PAB △的直线上, 由正弦定理,可得PAB △外接圆的半径为122sin603PA r =⨯=所以三棱锥C PAB -外接球的半径为22222162233AC R r ⎛⎫⎛⎫=++= ⎪ ⎪⎝⎭⎝⎭ 所以三棱锥C PAB -外接球的表面积为2216644433S R πππ==⨯=, 即三棱锥P ABC -外接球的表面积为2216644433S R πππ==⨯=. 故选:B.7.(2022·福建龙岩·高一期中)已知三棱锥A -BCD 中,22CD =2BC AC BD AD ====,则此几何体外接球的表面积为( ) A .23πB .2πC 82πD .8π【答案】D 【解析】 【分析】根据三棱锥的几何特点计算出三棱锥外接球的半径,即可计算出表面积. 【详解】如图,O 为CD 的中点,根据题意,BCD △和ACD △都是直角三角形,且 2OA OB OC OD ===O ∴是三棱锥外接球的球心,且外接球的半径2R OA =所以外接球的表面积为:24?8S R ππ==. 故选:D.8.(2022·湖南·雅礼中学高一期中)在正三棱锥P ABC -中,23AB =正三棱锥P ABC -的体积是43P ABC -外接球的表面积是( ) A .5π B .15πC .25πD .35π【答案】C【分析】根据体积求得锥体高度,利用正弦定理求出底面所在的圆的半径,结合勾股定理求得外接球的半径,即可求出其表面积. 【详解】如图所示,设点G 为ABC 的外心,则PG ⊥平面ABC ,由13P ABC ABCV SPG -=⋅=1132334332PG ⨯⨯= ∴4PG =,则三棱锥P ABC -的外接球的球心O 在直线PG 上.设其外接球的半径为R , 由正弦定理得22sin3AB AG π==,在Rt OAG 中,|||4|OG PG R R =-=-,由勾股定理得222OA OG AG =+,即2222|4|R R =+-,解得52R =. 正三棱锥P ABC -外接球的表面积是22544252S R πππ⎛⎫==⨯= ⎪⎝⎭,故选:C .二、多选题9.(2022·浙江宁波·高一期中)已知点,,,A B C D 是半径为2的球面上不共面的四个点,且23AB CD ==,则四面体ABCD 体积的值可能为( )A .3B .4C .43D .6【答案】AB 【解析】 【分析】设球心为O ,,E F 分别为,AB CD 中点,根据球心的特征可知求得1OE OF ==,知,E F 是以O 为球心,1为半径的球面上的点,从而得到02EF OE OF <+=≤,利用三棱锥体积公式可确定223A BCD A CDE CDEV V S d --==⋅,结合3d AE =≤CDE △边CD 上的高2h EF ≤≤可求得体积最大值,由此确定选项.设O 为,,,A B C D 所在球面的球心,,E F 分别为,AB CD 中点,2OA OC .3AB CD ==OE AB ∴⊥,OE CD ⊥且3AE CF ==1OE OF ∴==,则,E F 均是以O 为球心,1为半径的球面上的点,则02EF OE OF <+=≤,E 是AB 中点,223A BCD A CDE CDEV V S d --∴==⋅(d 为点A 到平面CDE 距离,3d AE ≤, 又12CDESCD h =⋅(h 为点E 到CD 距离,2h EF ≤≤), 2232343A BCD V -⨯∴=≤,当且仅当,,E O F 三点共线且AB CD ⊥时等号成立.故选:AB . 【点睛】关键点点睛:本题考查立体几何中的外接球相关问题的求解,解题关键是能够确定,AB CD 中点,E F 是以O 为球心,1为半径的球面上的点,从而能够确定点A 到平面CDE 距离和点E 到CD 距离的范围,利用棱锥体积公式可求得体积的最大值.10.(2022·福建师大附中高一期中)在直三棱柱111ABC A B C -中,3ABC π∠=,1AC AA =,若该三校柱的外接球的表面积为28π,则该三棱柱的体积不可能是( ) A .15 B .18 C .21 D .24【答案】CD 【解析】 【分析】设1AC AA m ==,求得ABC 的外接圆的半径3r =结合球的表面积公式和球的截面性质,列出方程求得23m =ABC 面积的最大值,根据柱体的体积公式求得棱柱的最大体积,结合选项,即可求解. 【详解】如图所示,设1AC AA m ==, 在ABC 中,3ABC π∠=,AC m =,所以外接圆的半径23sin3m r π==3r = 取上底面111A B C △和下底面ABC 的外心,分别为21,O O ,连接12O O ,取得12O O 的中点O ,可得O 为直三棱柱111ABC A B C -的外接球的球心, 设直三棱柱111ABC A B C -的外接球的半径为R ,可得2428R ππ=,解得27R =,在1BOO 中,可得22211OB O B OO =+,即222(()723m R =+=,解得212m =,所以23m =111ABC A B C -的高为3在ABC 中,由余弦定理得2222122cos23b c bc b c bc bc bc bc π=+-=+-≥-=,当且仅当b c =时,等号成立,所以12bc ≤, 所以ABC 的最大面积为max 1sin 3323S bc π==所以三棱柱111ABC A B C -的体积的最大值为332318V Sh ==. 所以三棱柱111ABC A B C -不可能为21和24. 故选:CD.11.(2022·浙江省定海第一中学高一期中)数学中有许多形状优美、寓意独特的几何体,“等腰四面体”就是其中之一,所谓等腰四面体,就是指三组对棱分别相等的四面体.关于“等腰四面体”,以下结论正确的是( ) A .长方体中含有两个相同的等腰四面体B .“等腰四面体”各面的面积相等,且为全等的锐角三角形C .“等腰四面体”可由锐角三角形沿着它的三条中位线折叠得到D .三组对棱长度分别为a ,b ,c 的“等腰四面体”222a b c ++【答案】ABC 【解析】【分析】作出长方体,根据等腰四面体的定义得出图形,根据长方体的性质判断各选项. 【详解】如图,长方体1111ABCD A B C D -有两个相同的等腰四面体:11ACB D 和11AC BD ,A 正确;如等腰四面体11AC BD 中,每个面可能看作是从长方体截一个角得出的, 如图,设11111,,A D A B AA 的长分别为,,x y z ,不妨设x y z ≥≥, 则2211B D x y +221AD x z +221AB y z +1BD 最大, 其所对角的余弦值为22222221122222222cos 02B AD y z x zy z x z∠==>+⋅++⋅+,最大角11B AD ∠为锐角,三角形为锐角三角形,同理其它三个面都是锐角三角形,各个面的三条边分别相等,为全等三角形,面积相等,B 正确;把一个等腰四面体沿一个顶点出发的三条棱剪开摊平,则得一个锐角三角形,还有三条棱是这个三角形的三条中位线,如等腰四面体11ACB D ,沿11,,AB AD AC 剪开摊平,11,ND PD 共线,同理可得,CM DP 共线,11,B M B N 共线,MNP △为锐角三角形(与等腰四面体11ACB D 的面相似),且1111,,B C B D CD 是这个三角形的中位线,因此C 正确;如上等腰四面体11AC BD 中三条棱长分别是长方体的三条面对角线长,由长方体性质知长2222a b c ++D 错。
四面体外接球表面积公式

四面体外接球表面积公式四面体是由四个面组成的立体图形,其中每个面都是一个三角形。
外接球是能够切过四面体的球,且球的表面刚好与四面体的每个面接触。
四面体外接球的表面积可以通过以下公式计算:S = 4πR²其中,S表示四面体外接球的表面积,π是圆周率(约等于3.14),R是外接球的半径。
为了理解这个公式,我们需要了解四面体和外接球的几何性质。
首先,四面体有几个重要的性质:1. 一个四面体有四个顶点、六条棱和四个面。
2. 如果一条线段既垂直于四面体的平面又垂直于四面体的一个面,那么这条线段称为四面体的高。
3. 四面体的高交于面的中心。
4. 四面体的三个面两两相交于一条线段,这些线段分别称为四面体的棱。
5. 四面体的棱的中点构成一个四面体的内接球的球心。
其次,我们需要了解外接球的性质:1. 外接球的球心位于四面体的高交点。
2. 外接球的球心到四面体的顶点的距离相等,都等于外接球的半径R。
3. 外接球的球心到四面体的面的距离也相等,也等于外接球的半径R。
4. 外接球的球面刚好与四面体的每个面接触,即球面上的每个点都和四面体的一个面相接触。
根据四面体和外接球的性质,我们可以推导得到四面体外接球的表面积公式。
首先确定外接球的半径R,这个半径就等于外接球的球心到四面体任意一个顶点的距离。
由于这个距离相等,我们可以任选一个顶点,假设它到外接球的球心的距离为R。
然后,计算外接球的表面积S。
由于外接球的球面刚好与四面体的每个面接触,所以四面体的每个面的面积等于外接球的球面的一部分。
我们可以将每个三角形的面积进行求和,即可得到外接球的表面积。
由于四面体的每个面都是一个三角形,三角形的面积可以用以下公式计算:A = 0.5 * a * h其中,A表示三角形的面积,a表示三角形的底边长,h表示三角形的高。
我们已经知道四面体的每个面都是一个三角形,所以可以计算出每个面的面积。
接下来,计算外接球的表面积。
由于球面的面积可以用以下公式计算:S = 4πR²其中,R表示外接球的半径。
2023学年上海高二数学上学期同步知识点 几何体的表面积、体积、轴截面、多面体与球体内切外接问题

重难点02 几何体的表面积、体积、轴截面、多面体与球体内切外接问题(重难点突破解题技巧与方法)1.求解几何体表面积的类型及求法求多面体的表面积只需将它们沿着棱“剪开”展成平面图形,利用求平面图形面积的方法求多面体的表面积求旋转体的表面积可以从旋转体的形成过程及其几何特征入手,将其展开后求表面积,但要搞清它们的底面半径、母线长与对应侧面展开图中的边长关系求不规则几何体的表面积通常将所给几何体分割成基本的柱体、锥体、台体,先求出这些基本的柱体、锥体、台体的表面积,再通过求和或作差,求出所给几何体的表面积2.求体积的常用方法直接法对于规则的几何体,利用相关公式直接计算割补法首先把不规则的几何体分割成规则的几何体,然后进行体积计算;或者把不规则的几何体补成规则的几何体,不熟悉的几何体补成熟悉的几何体,便于计算等体积法选择合适的底面来求几何体体积,常用于求三棱锥的体积,即利用三棱锥的任一个面可作为三棱锥的底面进行等体积变换3.几何体的外接球:一个多面体的顶点都在球面上即为球的外接问题,解决这类问题的关键是抓住外接球的特点,即球心到多面体的顶点的距离等于球的半径.几何体的内切球:求解多面体的内切球问题,一般是将多面体分割为以内切球球心为顶点,多面体的各侧面为底面的棱锥,利用多面体的体积等于各分割棱锥的体积之和求内切球的半径.4.截面问题:在高考立体几何考点中涉及到空间几何体的截面的地方较多,如:判断截面的形状、计算出空间几何体的截面周长或面积、或者求与之相关的体积问题、以及最值问题都在考察之列,但是要顺利地解决前面所提到的诸多问题,关键是根据题意作出截面,并判断其形状.能力拓展技巧方法题型一:柱、锥、台体的表面积、体积、轴截面 一、填空题1.(2021·上海·格致中学高二期中)已知一个圆锥的侧面展开图恰好是一个半圆,任取圆锥的两条母线a ,b ,则a ,b 所成角的最大值为______. 【答案】3π【分析】由题意可得圆锥的母线长R 和底面半径长r 的关系,可知轴截面是等边三角形,即可求解. 【详解】设圆锥的母线长为R ,底面半径长为r ,则222Rr ππ=,解得2R r =,所以圆锥的轴截面是等边三角形. 任取圆锥的两条母线a ,b ,如图:当a ,b 为轴截面的两条母线时,a ,b 所成角最大为3π. 故答案为:3π. 2.(2022·上海浦东新·高二期末)已知正三棱锥O ABC -的底面边长为4,高为2,则此三棱锥的体积为___________ 【答案】833【分析】根据题意条件,计算出底面积,然后再利用'13O ABC ABCV SOO -=⨯⨯,计算可求解出体积.【详解】如图,过O 点作底面ABC 的投影'O ,连接'OO ,取BC 的中点D ,连接AD ,在正三棱锥O ABC -中,底面ABC 为正三角形,边长为4,所以23AD = 1432ABCS AD BC =⨯⨯=,而'OO 为该正三棱锥O ABC -的高,长为2,所以'1833O ABC ABCV SOO -=⨯⨯=故答案为:833. 3.(2022·上海·复旦附中高二期中)如图所示,过三棱台上底面的一边11A C ,作一个平行于棱1BB 的截面,与下底面的交线为DE .若D 、E 分别是AB 、BC 的中点,则111111A B C DBE A B C ABCV V --=______.【答案】37【分析】证得11114A B C ABCSS =,然后结合棱台与棱柱的体积公式即可求出结果.【详解】因为1//BB 平面11DEC A ,且平面11BB C C平面111DEC A C E =,所以11//BB C E ,又因为11//B C BE ,所以四边形11BB C E 为平行四边形,所以11B C BE =,且E 分别是BC 的中点,所以1112B C BC =,同理1112A B AB =,因此11114A B C ABCS S =,设上底面的面积为S ,高为h ,则下底面的面积为4S ,所以()111111317443A B C DBEA B C ABCV ShV S S S S h --==+⋅+,故答案为:37.二、解答题4.(2021·上海·西外高二期中)设四边形ABCD 为矩形,点P 为平面ABCD 外一点,且P A ⊥平面ABCD ,若|P A |=|AB |=1,|BC |=2.(1)求四棱锥P -ABCD 的体积;(2)在BC 边上是否存在一点G ,使得点D 到平面P AG 2|BG |的值,若不存在,请说明理由;(3)若点E 是PD 的中点,在△P AB 内确定一点H ,使|CH |+|EH |的值最小,并求此时|HB |的值. 【答案】(1)23;(2)存在,|BG |=1;(3)位置答案见解析,值为53. 【分析】(1)根据棱锥的体积计算公式计算即可;(2)假设BC 边上存在一点G 满足题设条件,作DQ AG ⊥,可证明DQ ⊥平面PAG ,从而得到2DQ =,由此求解1BG =;(3)延长CB 到C ',使得C B CB '=,连结C E ',过E 作EE AD '⊥于E ',利用三点共线,两线段和最小,得到min ()CH EH +=C E ',过H 作HH AB '⊥于H ',连结HB ,在Rt △HH B '中,求解HB 即可.(1)由题可知112121333P ABCD ABCD V S PA -=⋅⋅=⨯⨯⨯=;(2)假设BC 边上存在一点G 满足题设条件,作DQ AG ⊥,则DQ ⊥P A , 则DQ ⊥平面PAG ,故2DQ =, 由1133P AGD D PAG AGDPAGV V SAP SDQ --=⇒⋅⋅=⋅⋅,则1122AD AB AP PA AG DQ ⋅⋅⋅=⋅⋅⋅ 则AD AB AG DQ ⋅=⋅ 则21|2AG⨯=⋅∣ 则2AG = 则22||211BG AG AB =-=-=故存在点G ,且当G 是BC 中点时,点D 到平面P AG 的距离为2,此时|BG |=1;(3)延长CB 到C ',使得C B CB '=,连结C E ',过E 作EE AD '⊥于E ', 则22141104CH EH C H EHC E EE C E '''''+=+=++ 当且仅当C '、H 、E 三点共线时等号成立,故min 41()2CH EH +=, 过H 作HH AB '⊥于H ',连结HB , 在Rt △HBH '中,13HH '=,23H B '=, ∴2222125()()333HB HH H B ''=+=+=. 5.(2021·上海·华东师范大学第三附属中学高二期中)如图所示,圆锥SO 的底面圆半径1OA =,母线3SA =.(1)求此圆锥的体积和侧面展开图扇形的面积;(2)如图,半平面SOA 与半平面SOP 所成二面角P SO A --大小为120,设线段SO 中点为M ,求异面直线AM 与PS 所成角的余弦值.【答案】(1)22,侧面展开图扇形的面积为3π73【分析】(1)利用锥体的体积公式以及扇形的面积公式可求得结果;(2)取OP 的中点E ,连接AE 、ME ,分析可知异面直线PS 与AM 所成的角为AME ∠或其补角,计算出AME △三边边长,利用余弦定理可求得结果. (1)解:由题意可知,2222SO SA OA - 圆锥SO 的体积为21223V OA SO π=⨯⨯=,该圆锥的侧面展开图扇形的面积为3S OA SA ππ'=⨯⨯=. (2)解:在圆锥SO 中,SO ⊥平面AOP ,AO 、PO ⊂平面AOP ,SO AO ∴⊥,SO PO ⊥,所以,二面角P SO A --的平面角为120AOP ∠=,取OP 的中点E ,连接AE 、ME ,E 、M 分别为PO 、SO 的中点,则//ME PS 且1322ME PS ==, 所以,异面直线PS 与AM 所成的角为AME ∠或其补角,3SA =,1OA =,则2222SO SA AO =-=,223AM AO OM ∴=+=,在AOE △中,12OE =,1OA =,120AOE ∠=, 由余弦定理可得2272cos1202AE AO OE AO OE =+-⋅=, 由余弦定理可得22273cos 218AM ME AE AME AM ME +-∠==⋅. 因此,异面直线AM 与PS 所成角的余弦值为7318. 6.(2021·上海市延安中学高二期中)如图,D 为圆锥的顶点,O 是圆锥底面的圆心,ABC 是底面的内接正三角形,P 为DO 上一点,90APC ︒∠=.(1)证明:PC ⊥平面PAB ;(2)设2DO =,圆锥的侧面积为23π,求三棱锥P ABC -的体积. 【答案】(1)证明见详解3【分析】(1)根据题意,先证明AB ⊥平面POC ,进而可得AB PC ⊥,,再结合090APC ∠=,即可证明PC ⊥平面PAB ;(2)根据题意,结合勾股定理与侧面积公式,即可求出圆锥底面半径为r 和母线长为l ,再根据棱锥的体积公式,即可求解.(1)证明:如图,连接CO 并延长,交AB 于点E .∵O 为ABC 外接圆的圆心,∴CE AB ⊥,即CO AB ⊥.在圆锥中,易知PO ⊥平面ABC ,∵AB 平面ABC ,∴PO AB ⊥,∵CO ⊂平面POC ,PO ⊂平面POC ,且CO PO O ⋂=,∴AB ⊥平面POC ,∴AB PC ⊥, ∵90APC ∠=︒,∴AP PC ⊥,又∵AB 平面PAB ,PA ⊂平面PAB ,且AB PA A ⋂=,∴PC ⊥平面PAB .(2)设圆锥底面半径为r ,母线长为l ,∵2DO =,且圆锥的侧面积为23π,∴222223r lrl ππ⎧+=⎪⎨=⎪⎩,解得26r l ⎧=⎪⎨=⎪⎩∵PA PC =,PA PC ⊥,∴22223PA AC r ==,即6PA =, ∵OA r =,∴3AB AC BC r ===,且2222PO PA OA r =-=, ∴333112663222332P ABC ABCrr V SPO -⋅=⋅⋅==题型二:多面体与球体内切外接问题 一、单选题1.(2021·上海·曹杨二中高二阶段练习)半径为5的球内有一个高为8的正四棱锥,则该球与该内接正四棱锥体积之比为( ) A .2564πB .12564πC .12516πD .1254π【答案】B【分析】由题意画出图形,设正四棱锥P ABCD -,AC 的中点为E ,连接PE 并延长交球于G ,得8PE =,10PG =,根据2·PA PE PG =求出PA ,再由勾股定理求出球内接正四棱锥的底面边长AB ,最后根据球的体积公式和棱锥的体积公式,分别求出球与该内接正四棱锥的体积,即可得出答案. 【详解】解:由题可知,正四棱锥的高为8,外接球半径为5,如图,设正四棱锥P ABCD -,AC 的中点为E ,连接PE 并延长交球于G ,可知PE ⊥底面ABCD ,且PA AG ⊥,则8PE =,10PG =, cos PE PAAPE PA PG∴∠==,即2·80PA PE PG ==,得45PA =,2280648AC AE ∴==-=,28422AB ∴=⨯=, ∴球的体积为:41253V π=⨯,该内接正四棱锥体积为:21256(42)833P ABCD V -=⨯⨯=,∴球与该内接正四棱锥的体积之比为:41251253256643P ABCDV V ππ-⨯==. 故选:B.2.(2021·上海市复兴高级中学高二期中)在三棱锥A BCD -中,7AB BC CD DA ====23BD =面角A BD C --是钝角.若三棱锥A BCD -的体积为2.则三棱锥A BCD -的外接球的表面积是( ) A .12π B .373π C .13π D .534π 【答案】C【分析】取BD 的中点O ,可得AOC ∠为二面角A BD C --的平面角且BD ⊥平面AOC ;利用三棱锥A BCD -体积可构造方程求得AC ,将三棱锥A BCD -补为长方体BMDG HCFA -,则长方体外接球即为三棱锥的外接球,通过求解长方体外接球表面积即可得到结果. 【详解】如图(1),取BD 的中点O ,连接,AO CO ,AB BC CD DA ===,AO BD ∴⊥,CO BD ⊥,AOC ∴∠为二面角A BD C --的平面角,BD ⊥平面AOC .取AC 的中点E ,连接OE ,设AC 2a =,在AOC △中,732AO OC ==-=,OE AC ∴⊥, 则22224OE a a =-=-, 21111232423326A BCD AOCV SBD AC OE BD a a -∴=⋅=⨯⨯⨯⨯=⨯⨯⨯-=,化简得:42430a a -+=,解得:3a =或1a =, 当1a =时,60AOC ︒∠=,不合题意,舍去,23∴=AC .图(1) 图(2)如图(2),把三棱锥A BCD -补形成长方体BMDG HCFA -,使三棱锥A BCD -的各棱分别是长方体的面对角线,则三棱锥A BCD -的外接球即为长方体BMDG HCFA -的外接球. 设,,BM x BG y BH z ===,则222222222(23)(7)(7)x y x z y z ⎧+=⎪⎪+=⎨⎪+=⎪⎩,解得:661x y z ⎧=⎪⎪=⎨⎪=⎪⎩,外接球的直径为22213AM x y z =++=, 四面体ABCD 外接球的表面积为134134S ππ=⨯=. 故选:C .【点睛】本题考查三棱锥外接球表面积的求解问题,涉及到三棱锥体积的应用;解题关键是能够通过将三棱锥补为长方体,通过求解长方体的外接球来求得结果.3.(2021·上海市松江二中高二期中)已知一圆锥底面圆的直径为333个棱长为a 的正四面体,并且正四面体在该几何体内可以任意转动,则a 的最大值为( ) A .3 B 2C .9322D .322【答案】B【分析】根据题意,该四面体内接于圆锥的内切球,通过内切球即可得到a 的最大值. 【详解】依题意,四面体可以在圆锥内任意转动,故该四面体内接于圆锥的内切球设球心为P ,球的半径为r ,下底面半径为R ,轴截面上球与圆锥母线的切点为Q ,圆锥的轴截面如图:则32OA OB ==,因为332SO =, 故可得:223SA SB SO OB ==+=;所以SAB △为等边三角形,故P 是SAB △的中心, 连接BP ,则BP 平分SBA ∠, 所以30PBO ∠=︒; 所以tan 30r R︒=,即33333322r R ==⨯=, 即四面体的外接球的半径为32r =. 另正四面体可以从正方体中截得,如图:从图中可以得到,当正四面体的棱长为a 2, 而正四面体的四个顶点都在正方体上,故正四面体的外接球即为截得它的正方体的外接球, 所以126233r AA =,所以2a =即a 2 故选:B .【点睛】本题考查了正四面体的外接球,将正四面体的外接球转化为正方体的外接球,是一种比较好的方法,本题属于难题. 二、填空题4.(2021·上海市控江中学高二期中)直三棱柱111ABC A B C -的所有顶点都在球O 的球面上,AB BC ⊥,1AB =,22BC =14AA =,则球O 的体积是__________.【答案】1256π 【分析】把直三棱柱111ABC A B C -补成长方体,求出外接球的直径即得解.【详解】把直三棱柱111ABC A B C -补成长方体,则直三棱柱和长方体的外接球重合,外接球的直径25R =,故球O 的体积3412536V R ππ==. 故答案为:1256π 5.(2021·上海·华师大二附中高二期中)已知三棱锥A BCD -的侧棱两两互相垂直,且该三棱锥的外接球的体积为36π,则该三棱锥的侧面积的最大值为________. 【答案】18【分析】由题意将该三棱锥补成一个长方体,由球的体积公式可得外接球的半径R ,令AB x =,AC y =,AD z =,进而可得22236x y z ++=,再利用基本不等式即可得解.【详解】由题意以该三棱锥的三条侧棱为长、宽、高,将该三棱锥补成一个长方体,长方体的体对角线就是外接球的直径,令AB x =,AC y =,AD z =,外接球的半径为R ,根据三棱锥外接球的体积为34363R ππ=,可得球的半径3R =,则()2222236R x y z =++=, 所以该三棱锥的侧面积S 111222yz xy xz =++ ()()()()2222222221111184442y z x y x z x y z ≤++++++=+=,当且仅当x y z ===. 故该三棱锥的侧面积的最大值为18. 故答案为:18.【点睛】本题考查了几何体的外接球相关问题的求解及基本不等式的应用,考查了运算求解能力与转化化归思想,属于中档题.6.(2021·上海·高二专题练习)如图,边长为2的正方形ABCD 中,点E 、F 分别是边AB 、BC 的中点,AED ∆、EBF ∆、FCD ∆分别沿DE 、EF 、FD 折起,使A 、B 、C 三点重合于点A ',若四面体A EFD '的四个顶点在同一个球面上,则该球的表面积为________.【答案】6π【分析】把棱锥扩展为正四棱柱,求出正四棱柱的外接球的半径,就是三棱锥的外接球的半径,由此能求出该球的表面积,得到答案.【详解】由题意,知A EF '∆是等腰直角三角形,且A D '⊥平面A EF ', 三棱锥的底面A EF '扩展为边长为1的正方形,然后扩展为正四棱柱,三棱锥和外接球与正四棱柱的外接球是同一个球, 正四棱柱的对角线长就是外接球的直径, 所以球的半径222112622R ++==, 所以该球的表面积为22644()62S R πππ==⨯=. 故答案为6π.【点睛】本题主要考查了球的表面积的求法,同时考查空间几何体的结构特征的应用,着重考查了推理与论证能力,以及运算能力,属于中档试题.7.(2021·上海市西南位育中学高二期中)已知三棱锥P ABC -中,PA PB PC 、、两两垂直,且长度相等,若P A B C 、、、都在半径为1的同一球面上,则球心到平面ABC 的距离为__________. 【答案】13【分析】由弥补法知三棱锥P ABC -的外接球为以PA PB PC 、、为相邻三条棱的正方体的外接球,球心到平面ABC 的距离即为正方体中心到平面ABC 的距离,利用等体积法可求得P 到平面ABC 的距离,进而求得答案.【详解】因为三棱锥P ABC -中,PA PB PC 、、两两垂直,且长度相等,所以此三棱锥的外接球即为以PA PB PC 、、为相邻三条棱的正方体的外接球,又球的半径为1,所以正方体的棱长为233,即233PA PB PC ===球心到平面ABC 的距离即为正方体中心到平面ABC 的距离, 设P 到平面ABC 的距离为h ,则正三棱锥P ABC -的体积3111123()33323ABCPABV Sh SPC =⋅=⋅=⨯⨯等边ABC 的边长为22232326+=333⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,21263232323ABCS⎛⎫∴=⨯⨯= ⎪ ⎪⎝⎭3311231123()()232332313123333ABC h S ⨯⨯⨯⨯∴===⨯所以球心到平面ABC 的距离为13故答案为:13【点睛】方法点睛:空间几何体与球接、切问题的求解方法(1)求解球与棱柱、棱锥的接、切问题时,一般过球心及接、切点作截面,把空间问题转化为平面图形与圆的接、切问题,再利用平面几何知识寻找几何中元素间的关系求解.(2)若球面上四点P ,A ,B ,C 构成的三条线段 两两互相垂直,一般把有关元素“补形”成为一个球内接长方体,利用长方体的外接球求解.8.(2022·上海奉贤区致远高级中学高二期末)设A B C D ,,,是同一个半径为4的球的球面上四点,ABC 为等边三角形且其面积为93,则三棱锥D ABC -体积的最大值为___________. 【答案】183【分析】求出等边ABC 的边长,画出图形,判断D 的位置,然后求解即可. 【详解】ABC 为等边三角形且其面积为93,则23934ABCSAB ==,6AB ∴= 如图所示,设点M 为ABC 的重心,E 为AC 中点,当点D 在平面ABC 上的射影为M 时,三棱锥D ABC -的体积最大,此时,4OD OB R ===,点M 为三角形ABC 的重心,2233BM BE ∴==,Rt OMB ∴中,有222OM OB BM -=,426DM OD OM ∴=+=+=,所以三棱锥D ABC -体积的最大值19361833D ABC V -=⨯⨯=故答案为:183【点睛】思路点睛:本题考查球的内接多面体,棱锥的体积的求法,要求内接三棱锥体积的最大值,底面是面积一定的等边三角形,需要该三棱锥的高最大,故需要DM ⊥底面ABC ,再利用内接球,求出高DM ,即可求出体积的最大值,考查学生的空间想象能力与数形结合思想,及运算能力,属于中档题. 三、解答题9.(2021·上海·华师大二附中高二期中)已知正方体1111ABCD A B C D -.(1)若正方体的棱长为1,求点A 到平面1A BD 的距离;(2)在一个棱长为10的密封正方体盒子中,放一个半径为1的小球,任意摇动盒子,求小球在盒子中不能达到的空间的体积;(3)在空间里,是否存在一个正方体,它的定点1111A B C D A B C D 、、、、、、、到某个平面的距离恰好为0、1、2、3、4、5、6、7,若存在,求出正方体的棱长,若不存在,说明理由. 【答案】3()3761043cm π-(3)21【分析】(1)利用等体法:11A A BD A ABD V V --=即可求解.(2)求出小球在正方体的8个顶点以及12条棱处不能到达的空间,利用球的体积公式以及柱体体积公式即可求解.(3)设平面α为符合题意的平面,α过点C ,延长1111,,D C A B AB 分别交平面α于点,,E F G ,由题意可得1111::::::1:2:3:4:5:6:7C E BG B F DC D E AG A F =,设正方体的棱长为4a ,根据11C ECF C EC F V V --=,求出点1C 到平面α的距离,进而得出正方体的棱长.(1)正方体的棱长为1,设点A 到平面1A BD 的距离为h , 由11A A BD A ABD V V --=,则111133A BDABDS h SAA⋅=⋅,即11111113232⨯=⨯⨯⨯⨯, 解得h (2)在正方体的8个顶点处的单位立方体空间内,小球不能到达的空间为:331448118833ππ⎡⎤⎛⎫-⨯=- ⎪⎢⎥⎝⎭⎣⎦, 除此之外,以正方体的棱为一条棱的12个118⨯⨯的正四棱柱空间内, 小球不能到达的空间共()21121181896244ππ⎡⎤⨯⨯-⨯⨯=-⎢⎥⎣⎦,其它空间小球均能到达,故小球不能到达的空间体积为:4768962410433πππ-+-=- (3cm )(3)设平面α为符合题意的平面,α过点C , 延长1111,,D C A B AB 分别交平面α于点,,E F G , 由图可知,点1111,,,,,,,C C B B D D A A与平面α的距离分别应为0、1、2、3、4、5、6、7,因为11,,,D E A F DC AG 互相平行,所以它们与平面α所成角相等, 故由比例关系得1111::::::1:2:3:4:5:6:7C E BG B F DC D E AG A F =. 设正方体的棱长为4a ,则11,2,3C E a BGa B F a ===,用几何方法可解得EF =,,EC CF ==, 故2ECFS=,由1CC ⊥平面1111D C B A ,知1CC 为四面体1C EC F -的底面1EC F 上的高, 所以由11C ECF C EC F V V --=,算得点1C 到平面α的距离,121EC FECFSCC d S⋅===,实际上已知1d =1=,从而可得a = 所以正方体的棱长为4a =.10.(2019·上海·华师大二附中高二期中)平面图形很多可以推广到空间中去,例如正三角形可以推广到正四面体,圆可以推广到球,平行四边形可以推广到平行六面体,直角三角形也可以推广到直角四面体,如果四面体ABCD 中棱,,AB AC AD 两两垂直,那么称四面体ABCD 为直角四面体. 请类比直角三角形中的性质给出2个直角四面体中的性质,并给出证明.(请在结论1~3中选择1个,结论4,5中选择1个,写出它们在直角四面体中的类似结论,并给出证明,多选不得分,其中h 表示斜边上的高,,r R 分别表示内切圆与外接圆的半径) 直角三角形ABC直角四面体ABCD条件 AB AC ⊥,,AB AC AB AD AC AD ⊥⊥⊥结论1 222AB AC BC +=结论2 22sin sin 1B C += 结论3222111h AB AC =+结论4 1111AB AC h r ++=结论5 ()()2222122R AB BC CA =++【分析】结论1:分别表示222123S S S 、、,然后证明2222123S S S S ++=结论2:在DAE △中利用等面积法,表示出高d ,然后分别表示222sin sin sin αβγ、、,再证明222sin sin sin 1αβγ++=结论3:利用结论2中得到的d 的表达式,再表示出222111AB AC AD 、、,再证明22221111d AB AC AD =++ 结论4:内切球的球心与四个顶点相连接,把三棱锥分成四个小的三棱锥,利用D ABC O ABC O ABD O ACD O BCD V V V V V -----=+++进行证明结论5:将直角四面体ABCD 补形成为以AB AC AD 、、为长、宽、高的长方体,再进行证明. 【详解】记ABC ABD ACD BCD 、、、的面积依次为123S S S S 、、、, 平面BCD 与AB AC AD 、、所成角依次为αβγ、、,点A 到平面BCD 的距离为d r R ,,分别表示内切球与外接球的半径,内切球的球心为O , 直角三角形ABC直角四面体ABCD条件 AB AC ⊥AB AC AB AD AC AD ⊥⊥⊥,,结论1222AB AC BC += 2222123S S S S ++=结论2221sin B sin C +=222sin sin sin 1αβγ++=结论3222111h AB AC =+ 22221111d AB AC AD =++结论41111AB AC h r ++=11111AB AC AD d r +++=结论5 ()()2222122R AB BC CA =++()22222R AB BC CA =++证明:设AB a AC b AD c ===、、,过A 作AE BC ⊥,垂足为E ,联结DE ,过A 作AH DE ⊥,垂足为H ,易证:DE BC ⊥,AH ⊥平面BCD ,则d AH =,结论1:()22222222222212311112224S S S ab ac bc a b a c b c ⎛⎫⎛⎫⎛⎫++=++=++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,在Rt ABC 中,22AB ACAE BCa b ⋅==+2222222a b DE AD AE c a b=+=++()2222222222222221=214a b a c b a b S a b c a b c ⎛⎫+⋅+= ⎪ ⎪+⎝++⎭s 2222123S S S S ∴++=;结论2:2222222222222abc AD AE abc a bd AH DE a b a b a c b c c a b ⋅⋅+====++++, ∴222222sin d bcaa b a c b c α==++. 同理,222222sin ac a b a c b c β=++,222222sin ab a b a c b c λ=++∴222222222222222sin sin sin 1b c a c a b a b a c b c αβγ++++==++; 结论3:∵222222abc d a b a c b c =++,∴22222222221a b a c b c d a b c ++=,又222222222222222111111b c a c a b AB AC AD a b c a b c ++++=++=, ∴22221111d AB AC AD =++ 结论4:D ABC O ABC O ABD O ACD O BCD V V V V V -----=+++,∴222222111111111632323232abc ab r ac r bc r a c b c a b r =⋅⋅+⋅⋅+⋅⋅+⋅++⋅. 从而22222211111ab ac bc a c b c a b r abc abc abc abc c b a d++=+++=+++,即11111r AB AC AD d =+++; 结论5:将直角四面体ABCD 补形成为以AB AC AD 、、为长、宽、高的长方体,则长方体的体对角线即为直角四面体ABCD 的外接球的直径,即()22222R AB BC CA =++.【点睛】本题考查平面图形向立体图形的推广,涉及到侧面积的表示,线面角的表示,几何体的体积分割法求内切球半径,补齐几何体求外接球半径等,属于难题.一、单选题1.(2022·上海市杨浦高级中学高二期末)大数学家阿基米德的墓碑上刻有他最引以为豪的数学发现的象征图——球及其外切圆柱(如图).以此纪念阿基米德发现球的体积和表面积,则球的体积和表面积均为其外切圆柱体积和表面积的( )巩固练习A .13B .12C .23D .34【答案】C【分析】设球的半径为R ,则圆柱的底面半径为R ,高为2R ,分别求出球的体积与表面积,圆柱的体积与表面积,从而得出答案.【详解】设球的半径为R ,则圆柱的底面半径为R ,高为2R 所以球的体积为343R π, 表面积为24R π. 圆柱的体积为:3222R R R ππ⨯=,所以其体积之比为:3342323RR ππ= 圆柱的侧面积为:2224R R R ππ⨯=, 圆柱的表面积为:222426R R R πππ+=所以其表面积之比为:224263R R ππ= 故选:C2.(2022·上海·复旦附中高二期中)为提高学生数学学习的积极性,复旦附中联合浦东分校、青浦分校、复旦中学组织了复旦附中月度数学学科知识竞赛.本次比赛的年度总冠军奖杯由一个铜球O 和一个底座组成,如图(1)所示,已知球的体积为36π,底座由边长为12的正三角形铜片ABC 沿各边中点的连线垂直向上折叠成直二面角所得,如图(2)所示.则在图(1)所示的几何体中,下列结论中正确的是( )A .CD 与BE 是异面直线B .异面直线AB 与CD 所成角的大小为45°C .由A 、B 、C 三点确定的平面截球所得的截面面积为3πD .球面上的点到底座底面DEF 的最大距离为336++ 【答案】C【分析】取,DF EF 中点N ,M ,利用给定条件证明//,//BC DE AB DF ,推理判断A ,B ;求出ABC 外接圆半径,结合球面截面圆性质计算判断C ,D 作答.【详解】取,DF EF 中点N ,M ,连接,,,,,AB BC AC BM MN CN ,如图,因BEF 为正三角形,则BM EF ⊥,而平面BEF ⊥平面DFE ,平面BEF 平面DFE EF =,BM ⊂平面BEF ,于是得BM ⊥平面DFE ,同理CN ⊥平面DFE ,即//BM CN ,33BM CN ==因此,四边形BCNM 是平行四边形,有////BC NM DE ,则直线CD 与BE 在同一平面内,A 不正确; 由选项A ,同理可得//AB DF ,则异面直线AB 与CD 所成角等于直线DF 与CD 所成角60,B 不正确; 由选项A 知,132BC MN DE ===,同理可得3AB AC ==,正ABC 外接圆半径3r = 由A 、B 、C 三点确定的平面截球所得的截面圆是ABC 的外接圆,此截面面积为3π,C 正确; 体积为36π的球半径R ,由34363R ππ=得3R =,由选项C 知,球心到平面ABC 的距离226d R r =-=由选项A ,同理可得点A 到平面DFE 的距离为33ABC 与平面DFE 的距离为33的点到底座底面DEF 的最大距离为3336R d BM ++=+D 不正确. 故选:C【点睛】易错点睛:异面直线所成的角的取值范围是π0,2⎛⎤⎥⎝⎦,当求出角的余弦值为负时,要取其相反数作为异面直线夹角余弦. 二、填空题3.(2022·上海交大附中高二阶段练习)己知正三棱锥的底面边长为4,高为2,则三棱锥的表面积是_________. 【答案】3【分析】画出图形,求出底面积和侧面积,从而求出表面积.【详解】如图,正三棱锥O -ABC ,高OM =2,取BC 中点N ,连接AN ,ON ,则M 在线段AN 上,且13MN AN =,由AB =4,BN =2,由勾股定理得:16423AN =-=,所以12333MN AN ==,2222343433ON OM MN ⎛⎫=+=+= ⎪ ⎪⎝⎭,所以18323OBCS BC ON =⋅=,1432ABCS BC AN =⋅=,所以三棱锥的表面积为833431233⨯+=. 故答案为:1234.(2018·上海市金山中学高二期中)已知长方体的三条棱长分别为,,,并且该长方体的八个顶点都在一个球的球面上,则此球的表面积为____________. 【答案】6π【详解】22226621126,4(6R R S ππ=++=∴==球5.(2022·上海市建平中学高二阶段练习)正四面体边长为4,则其体积为_________ 162【分析】由正四面体性质求体高,再应用棱锥的体积公式求体积即可. 【详解】由正四面体的体高为h 22161223h h --46h = 所以体积为214613162432⨯=1626.(2021·上海市市西中学高二期中)如图,在正三角形ABC 中,E 、F 依次是AB 、AC 的中点,AD ⊥BC ,EH ⊥BC ,F G⊥BC ,D 、H 、G 为垂足,若将正三角形ABC 绕AD 旋转一周所得的圆锥的体积为V ,则其中由阴影部分所产生的旋转体的体积与V 的比值是______________.【答案】58【分析】利用圆锥的体积公式及圆柱的体积公式即求.【详解】由题可知由阴影部分所产生的旋转体的体积为将正三角形ABC 绕AD 旋转一周所得的圆锥的体积与四边形EFGH 旋转一周所得的圆柱的体积的差,设圆锥的高为h ,底面半径为r ,则圆柱的高为2h,底面圆的半径为2r ,则2252211183r h V V V VV r h ππ⎛⎫⋅⎪-⎝⎭=-=-=圆柱圆柱, 即由阴影部分所产生的旋转体的体积与V 的比值是58.故答案为:587.(2021·上海市南洋模范中学高二期中)一矩形的一边在x 轴上,另两个顶点在函数22(0)1xy x x =>+的图像上,如图,则此矩形绕x 轴旋转而成的几何体的体积的最大值是___________.【答案】π【分析】先利用基本不等式求出y 的取值范围,再设点A ,B 的坐标,由A ,B 的纵坐标相同,得到121=x x ,从而得到h ,再利用圆柱的体积公式以及基本不等式,即可得到答案. 【详解】由22211x y x x x==++,又0x >,则1122x x x x +≥⋅=,当且仅当1x =时取等号, ∴222111x y x x x==≤++,且12x x y+=, ∵矩形绕x 轴旋转而成的几何体为圆柱,设A 1(x ,1)y ,2(B x ,2)y ,如图所示,则圆柱的底面圆的半径为y ,高为21h x x =-,且()112121x f x x =+,()222221x f x x =+, ∴1222122211x x x x =++,即()()211210x x x x --=,由12x x ≠,可得121=x x , ∴()()222212121212114444h x x x x x x x x y ⎛⎫=-=+-=+-=- ⎪⎝⎭,故222144y h y y-=-=, ∴圆柱的体积为()()22222212124y y V y h y y ππππ+-==-≤⋅=,当且仅当22y =时取等号, ∴此矩形绕x 轴旋转而成的几何体的体积的最大值是π. 故答案为:π.8.(2021·上海市南洋模范中学高二期中)如图,已知半径为2的球O 的直径AB 垂直于平面α,垂足为B ,△BCD 是平面α内边长为2的正三角形,线段AC ,AD 分别与球面交于点M ,N ,则三棱锥A BMN -的体积为___________.【答案】【分析】由已知证明三角形相似可得AM AC =45AN AD =,得到求出三棱锥A BMN -的体积为把2R =代入得答案.【详解】2AB R =,BC R =,5AC R =,半径为R 的球O 的直径AB 垂直于面α,垂足为B ,△BCD 是面α内边长为R 的正三角形, 线段AC ,AD 分别与球面交于点M ,N ,BAM BAC ∴∠=∠,90AMB ABC ∠=∠=︒,则ABCAMB ,易知:45AM AC =,同理有45AN AD =,∴三棱锥A BMN -的体积为231613832253475A BMN V R R R -=⨯⨯⨯⨯=,又2R =,∴三棱锥A BMN -的体积为.故答案为:9.(2021·上海·格致中学高二期中)如图,有一个水平放置的透明无盖的正方体容器,容器高8cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm ,如果不计容器的厚度,则球的体积为______.【答案】5003π 【分析】设球的半径为R ,根据已知条件得出正方体上底面截球所得的截面圆的半径4AA '=,球心到截面圆圆心的距离2OA R '=-,利用勾股定理即可求出球的半径,再带入球体积公式即可.【详解】由题意得正方体上底面到水面的高为862-=,设球体的半径为R ,由题意如图所示:三角形OAA '为直角三角形,A 为球与正方体的交点,则2OA R '=-,842AA '==,OA R =,所以:222(2)4R R =-+,解得5R =, 所以球的体积33445005333V R =π=π⨯=π. 故答案为:5003π 10.(2021·上海·闵行中学高二期中)如图,三棱锥P ABC -的四个顶点都在球O 的球面上,PA PC ⊥,ABC。
空间几何体的表面积与体积公式大全,DOC
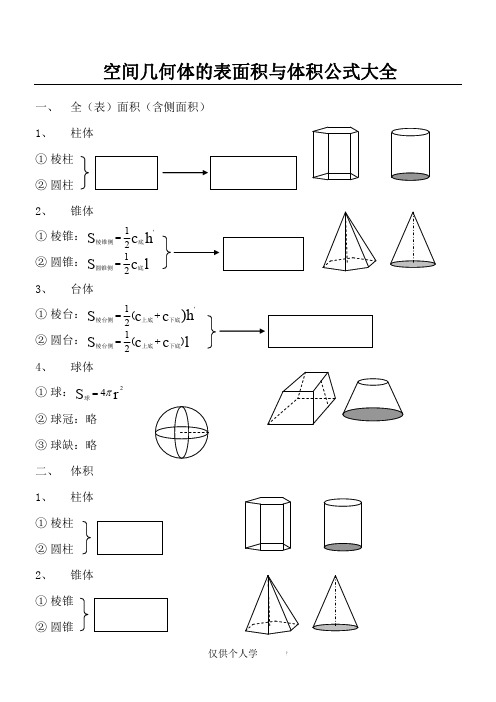
空间几何体的表面积与体积公式大全一、全(表)面积(含侧面积)1、①棱柱②圆柱2、①②3、①②4、①球:②③二、1、①棱柱②圆柱2、①棱锥②圆锥3、①棱台②圆台4、①球:②③三、1、2、则+=即底面直径和高相等的圆柱体积等于与它等底等高的圆锥与同直径的球体积之和 3、台体体积公式公式:)(31S SS S h V 下下上上台++=证明:如图过台体的上下两底面中心连线的纵切面为梯形ABCD 。
延长两侧棱相交于一点P 。
则∴V 即:)(33)(31S SS S h h S S S hS V 下下上上下上下上台++=++=∴)(31S S S S h V 下下上上台++=4、球体体积公式推导分析:将半球平行分成相同高度的若干层(层n ),n 越大,每一层越近似于圆柱,+∞→n 时,每一层都可以看作是一个圆柱。
这些圆柱的高为nr,则:每个圆柱的体积h S V i i ==nrr i 2π……=2r nr ⨯π=[3r n n π=[3r n n π当→n ∴V 半球5、 ∴S =球6、(1则其体积为:a V 3=正方体四个角上切下的每一个三棱锥体积为:中间剩下的正四面体的体积为:a a a a hSV 322231]60sin 21[3131)32232()2()2(=-⨯︒⨯⨯⨯==⨯⨯正三棱锥这样一个即:61(2 (a)(b)(c)(d)(e)(3(a ) 正方体内切球直径=正方体棱长(b ) 正方体内切球与正四面体的四条棱相切。
(c ) 与正四面体四条棱相切的球半径=正方体棱长的一半 (d ) 设正四面体棱长为a ,则与其棱都相切的球半径为r 1有:aar 422211=⨯= 7、利用祖暅原理推导球体体积。
构造一个几何体,使其截面与半球截面处处相等,根据祖暅原理可得两物体体积相等。
证明:作如下构造:在底面半径和高都是r 的圆柱内挖去一个与圆柱等底等高的圆锥。
如图:R ,∴S 1π=即:S 1 8、 正方体与球(1) 正方体的内切球正方体的棱长=a 球体的直径d (2) 正方体的外接球正方体的体对角线=a 3球体的直径d(3) 规律:①正方体的内切球与外接球的球心为同一点; ②正方体的内切球与外接球的球心在体对角线上; ③正四面体的内切球与外接球的的半径之比为:3:1 ④正四面体内切球与外接球体积之比为:1:339(∴a h r 12641==即:a a r V 33321663434)126(πππ===球∴π3:18=V V 球正四机体: (2)正四面体的外接球 外接球的半径=)2332(224343a a⨯-⨯=⨯高=a 46 ∴2:33122:86:33ππ==aaV V 正四面体球 (310、 (1 球体直径、圆柱的高、圆柱底面直径构成直角三角形。
高考数学专题《两招玩转多面体的外接球》填选压轴题及答案

专题60 两招玩转多面体的外接球【方法点拨】解决多面体的外接球问题的关键是“定心”,常用方法有两种:(1)“补体法”:对于符合特殊条件的四面体补形为长方体解决,常见的有下列两种类型. 类型一:墙角模型(三条线两个垂直,补形为长方体,其体对角线的中点即球心)方法:找三条两两垂直的线段,直接用公式2222)2(c b a R ++=,即2222c b a R ++=,求出R .类型二:对棱相等模型(补形为长方体)如下图,三棱锥(即四面体)中,已知三组对棱分别相等,求外接球半径(CD AB =,BC AD =,BD AC =)第一步:画出一个长方体,标出三组互为异面直线的对棱;第二步:设出长方体的长宽高分别为c b a ,,,x BC AD ==,y CD AB ==,z BD AC ==,列方程组,图3图12⎪⎩⎪⎨⎧=+=+=+222222222z a c y c b x b a ⇒2)2(2222222z y x c b a R ++=++=, 补充:abc abc abc V BCD A 31461=⨯-=- 第三步:根据墙角模型,22222222z y x c b a R ++=++=,82222z y x R ++=,8222z y x R ++=,求出R .(2)“窜心法”:多面体的外接球心问题,可转化为其某两个侧面三角形外接圆的垂线来解决,即球心就是分别过两个侧面三角形外接圆的圆心且垂直于该平面的直线的交点(即将三角形外接圆的圆心,垂直上蹿下跳).第一步:先画出如图所示的图形,将BCD ∆画在小圆上,找出BCD ∆和BD A '∆的外心1H 和2H ;第二步:过1H 和2H 分别作平面BCD 和平面BD A '的垂线,两垂线的交点即为球心O ,连接OC OE ,;第三步:解1OEH ∆,算出1OH ,在1OCH Rt ∆中,勾股定理:22121OC CH OH =+. 说明:解法二是通法,具体解题过程中,常常涉及复杂的线面位置关系的论证、多次解三角形等,有一定的难度.【典型题示例】例1 (2021·全国)已知三棱锥P ABC 的四个顶点在球O 的球面上,P A =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是P A ,AB 的中点,∠CEF =90°,则球O 的体积为( )A .86πB .46πC .26πD .6π图11【答案】D【解析】因为点E ,F 分别为P A ,AB 的中点,所以EF ∥PB ,因为∠CEF =90°,所以EF ⊥CE ,所以PB ⊥CE . 取AC 的中点D ,连接BD ,PD ,易证AC ⊥平面BDP ,所以PB ⊥AC ,又AC ∩CE =C ,AC ,CE ⊂平面P AC ,所以PB ⊥平面P AC , 所以PB ⊥P A ,PB ⊥PC ,因为P A =PB =PC ,△ABC 为正三角形,所以P A ⊥PC ,即P A ,PB ,PC 两两垂直,将三棱锥P ABC 放在正方体中如图所示.因为AB =2,所以该正方体的棱长为2,所以该正方体的体对角线长为6,所以三棱锥P ABC 的外接球的半径R =62,所以球O 的体积V =43πR 3=43π×(62)3=6π.故选D. 例 2 在边长为23的菱形ABCD 中,60A =︒,沿对角线BD 折起,使二面角A BD C --的大小为120°,这时点A ,B ,C ,D 在同一个球面上,则该球的表面积为____________. 【答案】28π【解析】设ABD 和BCD 的外心1O 和2O ,过1O 和2O 分别作平面ABD 和平面BCD 的垂线,两垂线的交点即为球心O (两垂线共面的证明,此处从略),连接OA 即为所求球的半径易知二面角A BD C --的平面角为AEC ∠(证明从略),故120AEC ∠=︒, 因为1O 是ABD 的外心,所以32332AE CE ==⨯=,11O E =,12O A = 在1Rt O OE ,11O E =,160OEO ∠=︒,所以13OO =, 在1Rt AOO ,2222211327OA OO O A =+=+= ∴四面体的外接球的表面积为2428R ππ=.CBD AE O 2O 1O例3 在三棱锥ABC P -中,5==BC PA ,17==AC PB ,10==AB PC ,则该三棱锥外接球的表面积为_________;外接球体积为_________. 【答案】3261326ππ,【解析】由题意,该三棱锥的对棱相等,可知该三棱锥可置于一个长方体中,记该长方体的棱长为c b a ,,,所以⎪⎩⎪⎨⎧=+=+=+251710222222c b c a b a ,即431===c b a ,,,所以22622591=++=r ,由此可得,326133426432ππππ====r V r S ,.例4 已知三棱锥P -ABC 的所有顶点都在球O 的球面上,△ABC 满足AB =22,∠ACB =90°,P A 为球O 的直径且P A =4,则点P 到底面ABC 的距离为( ) A. 2B.2 2C. 3D.23【答案】 B【解析】 取AB 的中点O 1,连接OO 1, 如图,在△ABC 中,AB =22,∠ACB =90°,所以△ABC 所在小圆圆O 1是以AB 为直径的圆, 所以O 1A =2,且OO 1⊥AO 1, 又球O 的直径P A =4,所以OA =2,所以OO 1=OA 2-O 1A 2=2,且OO 1⊥底面ABC , 所以点P 到平面ABC 的距离为2OO 1=2 2.【巩固训练】1.在三棱锥D ABC -中,平面ACD ⊥平面ABC ,AB ⊥AC ,且AC =CD =DA =3,AB =3,则三棱锥A BCD -的外接球的表面积为( ). A .15π4B .15πC .3π2D . 6π2.如下图,在四棱锥P ABCD -中,已知PA ⊥底面,,ABCD AB BC AD CD ⊥⊥,且120,2BAD PA AB AD ∠=︒===,则该四棱锥外接球的表面积为( )A .8πB .20πC .205πD . 205π33.三棱锥ABC P -中,平面⊥PAC 平面ABC ,△PAC 和△ABC 均为边长为2的正三角形,则三棱锥ABC P -外接球的半径为 .4.如图所示三棱锥,其中则该三棱锥外接球的表面积为 .2,则该正面体外接球的体积5.正四面体的各条棱长都为为 .6. 在三棱锥P ABC -中,PAB ∆是边长为3的等边三角形,AC BC =,90ACB ∠=︒,二面角P AB C --的大小为120︒,则三棱锥P ABC -外接球的表面积为 .7. 已知在四棱锥S -ABCD 中,SD ⊥底面ABCD ,且底面ABCD 是等腰梯形,BC //AD ,若SD =AD =8,BC =6,AB =CD =2,则四棱锥S -ABCD 的体积为 ;它的外接球的半径为 .(第一空2分,第二空3分)8.在三棱锥BCD A -中,,4,3,2======BD AC BC AD CD AB 则三棱锥BCD A -外接球的表面积为 .9.(多选题)在正六棱锥P ABCDEF -中,已知底面边长为1,侧棱长为2,则 A .AB PD ⊥ B .共有4条棱所在的直线与AB 是异面直线A BCD -5,6,7,AB CD AC BD AD BC ======CDCD .该正六棱锥的外接球的表面积为163π【答案或提示】1. 【答案】B甲乙 丙【解析】∵AB ⊥AC ∴△ABC 外接圆的圆心为BC 中点,∴A BCD -外接球的球心在过BC 中点且垂直于△ABC 所在平面的直线上如上图(乙)中,设BC 中点为O 1,球心为O ,同理,设△ADC 外接圆的圆心为O 2 则OO 2= O 1E =32, 在△OO 2D 中,O 2D =3,所以OD 2= O 1E 2+ O 2D 2=154所以三棱锥A BCD -的外接球的表面积为15π. 2. 【答案】B【解析】四边形ABCD 的外接圆的直径4AC =,故四棱锥外接球的球心在过AC 的中点且垂直于平面ABCD 的直线上,又因为P A 、两点在球面上,故其球心在过PA 中点且垂直于PA 的垂面上, 所以球心即为PC 中点(PAC 的外接圆即为大圆), 故PC 20π. 3. 【解析一】3460sin 22221===r r ,3221==r r ,312=H O , 35343121222=+=+=r H O R ,315=R .【解析二】312=H O ,311=H O ,1=AH , 352121222=++==O O H O AH AO R ,315=R . 4.【答案】55π【解析】同例2,设补形为长方体,三个长度为三对面的对角线长,设长宽高分别为c b a ,,,110493625)(2222=++=++c b a ,55222=++c b a ,5542=R ,π55=S .5. 【解析】这是对棱相等的特殊情况放入长方体中,32=R ,23=R ,ππ2383334=⋅=V . 6.【答案】13π【解析】取AB 的中点M ,连接PM 、CM , 因为PAB ∆是等边三角形,所以PM AB ⊥,又因AC BC =,所以CM AB ⊥,所以PMC ∠即为二面角P AB C --的平面角,即120PMC ∠=︒, 因为PAB ∆是等边三角形,所以PAB ∆的外接圆圆心即为三角形的重心1O ,过1O 作1l ⊥平面PAB ,而M 为ABC ∆的外接圆圆心,过M 作2l ⊥平面ABC , 所以1l 与2l 的交点即为三棱锥P ABC -外接球的球心O , 作平面PMC 截面图,则PM =,113O M ==,13O P == 而9030PMO PMC ∠=∠-︒=︒,则111tan302OO O M =⋅︒=,所以r OP == 所以三棱锥P ABC -外接球的表面积为2413r ππ=.7.【答案】563【提示】球心O 在SD 的中垂面上,所以O 到底面的距离d =4,设底面ABCD 的圆心为H ,半径为r ,1=,解得5r =,所以外接球的半径为R = 8.【答案】π229【解析】如“方法点拨类型二”图,设补形为长方体,三个长度为三对面的对角线长, 设长宽高分别为c b a ,,,则922=+b a ,422=+c b ,1622=+a c∴291649)(2222=++=++c b a ,291649)(2222=++=++c b a ,229222=++c b a ,22942=R ,π229=S . 9.【答案】BCD【解析】设底面中心为O ,PO ⊥平面ABCDEF ,PO AB ∴⊥.若PD AB ⊥,则AB ⊥平面POD ,则AB OD ⊥,即AB AD ⊥矛盾,A 错.AB 与,,,PC PD PE PF 异面,B 对.对于C ,可用几何法.设四棱锥内切球球心为1O ,1O ∴一定在PO上,图中OM =PMPO =AB 中点M ,连接,PM OM ,过1O 作1O H PM ⊥于点H ,1O H ∴⊥平面PABPM1只需11O HO O r ==,由122PO H PMO ⇒=△∽△⇒内切球球半径r =C 正确.设内切圆半径为r ,取AB 中点Q ,2PA PB ==,12BQ =,2PQ ∴==,Δ11224PAB S ∴=⋅⋅=,S ∴侧16112S =⨯⨯⨯=底Rt POQ △中,PO ===1132322r⎛∴⋅=+⋅ ⎝⎭,4r -∴=. 设外接球半径为R,则22)1R R-+=,R ∴=, 21643S πR π==,D 对,选BCD.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四面体外接球表面积公式
四面体是一个具有四个面的立体图形,可以被包围在一个球体的外部。
这个球体被称为四面体的外接球,它的半径和四面体的顶点之间的距离是相等的。
要计算四面体外接球的表面积,我们可以使用下面的公式:
S = 4πR^2
其中,S表示球体的表面积,R表示球体的半径。
在四面体的情况下,我们可以通过顶点的坐标来计算球体的半径。
首先,我们需要找到四面体的顶点。
设四面体的顶点分别为A、B、C 和D。
然后,我们可以通过计算AB、AC和AD的长度来确定球体的半径R。
接下来,我们可以使用球体表面积的公式来计算四面体外接球的表面积。
将半径R代入公式中,即可得到最终结果。
需要注意的是,四面体外接球的表面积只与球体的半径有关,而与四面体的具体形状无关。
因此,无论四面体的顶点如何排列,计算出的表面积都将是相同的。
四面体外接球的表面积公式是一个有用的工具,在几何学和工程学中广泛应用。
通过计算四面体外接球的表面积,我们可以更好地理解四面体的性质,并在实际问题中应用这些知识。
