根轨迹法(自动控制基本知识)
自动控制原理 第四章根轨迹

第四章根轨迹法4-1 根轨迹法的基本概念4-2 常规根轨迹的绘制法则4-3 广义根轨迹4-1 根轨迹法的基本概念一、根轨迹的概念根轨迹:系统中某个参数从零到无穷变化时,系统闭环特征根在s平面上移动的轨迹。
根指的是闭环特征根(闭环极点)。
根轨迹法是根据开环传递函数与闭环传递函数的关系,通过开环传递函数直接分析闭环特征根及系统性能的图解法。
K =0 s 1=0 s 2=-40 < K <1s 1 s 2为不等的负实根K =1s 1=-2 s 2=-21 < K < ∞s 1s2 实部均为-2由根轨迹可知:1)当K =0时,s 1=0,s 2=-1,这两点恰是开环传递函数的极点,同时也是闭环特征方程的极点.2)当0<K < 1 时,s 1,2都是负实根,随着k 的增长,s 1从s 平面的原点向左移,s 2从-1点向右移。
3) 当K = 1时, s 1,2= -2,两根重合在一起,此时系统恰好处在临界阻尼状态。
4) 1 <K <∞,s 1,2为共轭复根,它们的实部恒等于-2,虚部随着K 的增大而增大,系统此时为欠阻尼状态。
★在s平面上,用箭头标明K增大时,闭环特征根移动的方向,以数值表明某极点处的增益大小。
有了根轨迹图就可以分析系统的各种性能:(1)稳定性:根轨迹均在s的左半平面,则系统对所有K>0都是稳定的。
(2)稳态性能:如图有一个开环极点(也是闭环极点)s=0。
说明属于I型系统,阶跃作用下的稳态误差为0。
在速度信号V0t作用下,稳态误差为V0/K,在加速度信号作用下,稳态误差为∞。
(3)动态性能:过阻尼临界阻尼欠阻尼K越大,阻尼比ξ越小,超调量σ%越大。
由此可知:1、利用根轨迹可以直观的分析K的变化对系统性能的影响。
2、根据性能指标的要求可以很快确定出系统闭环特征根的位置;从而确定出可变参数的大小,便于对系统进行设计。
由以上分析知:根轨迹与系统性能之间有着密切的联系,但是,高阶方程很难求解,用直接解闭环特征根的办法来绘制根轨迹是很麻烦的。
自动控制原理 根轨迹法

n
i
|
注意
• 相角方程是决定系统闭环根轨迹的充分 必要条件 • 用相角方程绘制根轨迹; • 模值方程主要用来确定已知根轨迹上某 一点的K*值 • 例4-1,4-2
4.2 根轨迹绘制的基本法则
• 法则1: 根轨迹的分支数:根轨迹在[s]平面上的分支数 等于闭环 特征方程的阶数n,也就是分支数与闭环极点的 数目相同。
q
h
f
l
结论:1 零点、 2 极点、3 根轨迹增益
b0 ( s z1 )(s z 2 ) ( s zm ) G( s) H ( s ) K* a0 ( s p1 )(s p2 ) ( s pn )
• 根轨迹增益:
(s z ) (s p )
• 法则6: 根轨迹的起始角(从极点pk)和终止角(到零点zk) :
起始角:
例2 证2
m n
pk ( 2k 1) ( pk z j ) ( pk pi )
j 1 i 1 i k
终止角:
zk ( 2k 1) ( z k p i ) ( z k z j )
i
nm
0 ( 1) ( 2) 1 30
a
(2k 1)π π π , , π nm 3 3
d1 0.42, d 2 1.58(舍去)
s j
1 1 1 0 d d 1 d 2
1 G(s)H(s) 0即(s 3 3s 2 2s K * ) j 3 3 2 2 j K * 0
s2
0
常规根轨迹的绘制法则(P138) 终止于开环零点或。 1 根轨迹起始于开环极点或, 根轨迹对称实轴 2 根轨迹的条数为特征根的个数, 3 ∣n-m∣条渐近线对称于实轴,均起于实轴上的σa 点,
自动控制原理之根轨迹

2 G(s)H(s)=k(2s+1)/s(s+5)
写出根轨迹方程,求出对应的零点和极点。
k(2s +1)
1+
= 0,
s(s + 5)
系统2: 零点:-0.5 极点为0, -5 Kg=2k
1+ 2k(s + 0.5) = 0 s(s + 5)
第四章 线性系统的根轨迹法
4.2 根轨迹的绘制法则
【 根轨迹性质 1】 根轨迹是连续的 【 根轨迹性质 2】 根轨迹关于实轴是对称的
4
将特征根画在 s平面上
s1 -0.005 -0.4 -1 -1+j1.73 -1+j3.87
s2 -1.995 -1.6 -1 -1-j1.73 -1-j3.87
将特征根随增益的变化在s平 面上轨迹称为根轨迹
K=2 K=0.1 k=1
-2j
j k=0.1
-2
-1
0
-j
-2j
第四章 线性系统的根轨迹法
2个无穷远的零点
同理,对于 G(s)H (s) = k(s +1)(s + 2) s
1个无穷远的极点
第四章 线性系统的根轨迹法
【法则一】根轨迹的渐近线
根轨迹的渐近线限定了当根轨迹趋向于无穷远时,根轨 迹的走向与形状。即根轨迹沿一组渐近线趋向于无穷远
处的开环零点。
与正实轴的夹角记为 φa
2k +1 φa = n − m π (k = 0,1,..., n − m −1)
3
d1,2 =
2×3
= −1± 3
d1,2=-1.577,-0.422
d1 d2 是否均为分离点吗?
根轨迹法(自动控制原理)ppt课件精选全文完整版

课程:自动控制原理
第4章 根轨迹法
➢ 以K为参变量的根轨迹上的每一点都必须满足以上方程, 相应地,称之为‘典型根轨迹方程’。
也可以写成
m
n
(s zl ) K (s pi ) 0
可见,根轨迹可以清晰地描绘闭环极点与开环增益K之间的 关系。
课程:自动控制原理
第4章 根轨迹法
2.根轨迹的基本条件
❖ 考察图示系统,其闭环传递函数为:
Y(s) G(s) R(s) 1 G(s)H(s)
闭环特征方程为:
1 G(s)H(s) 0
➢ 因为根轨迹上的每一点s都是闭环特征方程的根,所以根轨 迹上的每一点都应满足:
l 1
i 1
对应的幅值条件为:
相角条件为:
n
( s pi ) K i1
m
(s zl )
l 1
m
n
(s zl ) (s pi ) (2k 1)180
k 1,2,
l 1
i 1
课程:自动控制原理
第4章 根轨迹法
❖ 上述相角条件,即为绘制根轨迹图的依据。具体绘制方法 是:在复平面上选足够多的试验点,对每一个试验点检查 它是否满足相角条件,如果是则该点在根轨迹上,如果不 是则该点不在根轨迹上,最后将在根轨迹上的试验点连接 就得到根轨迹图。
显然,位于实轴上的两个相邻的开环极点之间一定有分离 点,因为任何一条根轨迹不可能开始于一个开环极点终止 于另一个开环极点。同理,位于实轴上的两个相邻的开环 零点之间也一定有分离点。
课程:自动控制原理
第4章 根轨迹法
自动控制原理 第四章 根轨迹法
第4章 根 轨 迹 法根轨迹法是分析和设计线性控制系统的图解方法,使用简便,在控制工程上得到了广泛应用。
本章首先介绍根轨迹的基本概念,然后重点介绍根轨迹绘制的基本法则,在此基础上,进一步讨论广义根轨迹的问题,最后介绍控制系统的根轨迹分析方法。
4.1 根轨迹的基本概念4.1.1 根轨迹概念所谓根轨迹,就是系统开环传递函数的某一参数从零变化到无穷时,闭环特征根在s 平面上变化的轨迹。
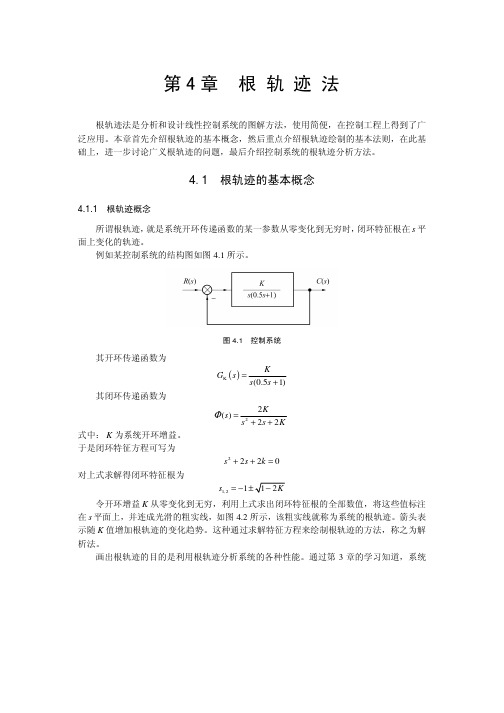
例如某控制系统的结构图如图4.1所示。
图4.1 控制系统其开环传递函数为()K (0.51)KG s s s =+其闭环传递函数为22()22Ks s s KΦ=++式中:K 为系统开环增益。
于是闭环特征方程可写为2220s s k ++=对上式求解得闭环特征根为1,21s =−令开环增益K 从零变化到无穷,利用上式求出闭环特征根的全部数值,将这些值标注在s 平面上,并连成光滑的粗实线,如图4.2所示,该粗实线就称为系统的根轨迹。
箭头表示随K 值增加根轨迹的变化趋势。
这种通过求解特征方程来绘制根轨迹的方法,称之为解析法。
画出根轨迹的目的是利用根轨迹分析系统的各种性能。
通过第3章的学习知道,系统第4章 根轨迹法·101··101·特征根的分布与系统的稳定性、暂态性能密切相关,而根轨迹正是直观反应了特征根在复平面的位置以及变化情况,所以利用根轨迹很容易了解系统的稳定性和暂态性能。
又因为根轨迹上的任何一点都有与之对应的开环增益值,而开环增益与稳态误差成反比,因而通过根轨迹也可以确定出系统的稳态精度。
可以看出,根轨迹与系统性能之间有着比较密切的联系。
图4.2 控制系统根轨迹4.1.2 根轨迹方程对于高阶系统,求解特征方程是很困难的,因此采用解析法绘制根轨迹只适用于较简单的低阶系统。
而高阶系统根轨迹的绘制是根据已知的开环零、极点位置,采用图解的方法来实现的。
下面给出图解法绘制根轨迹的根轨迹方程。
自动控制原理根轨迹法

21
二、根轨迹绘制的基本法则(4)
法则2
根轨迹的分支数和对称性 根轨迹的分支数与开环极点数n相等(n>m),或与开
环有限零点数m相等(n<m)。 根轨迹连续:根轨迹增益是连续变化导致特征根也连
续变化。 实轴对称:特征方程的系数为实数,特征根必为实数
或共轭复数。
22
二、根轨迹绘制的基本法则(5)
法则3
s(s 2.5)( s 0.5 j1.5)( s 0.5 j1.5)
试绘制该系统概略根轨迹。
解:将开环零、极点画在后面图中。按如下典型步骤
1)确定实轴上的根轨迹。本例实轴上区域
和
为轨迹。
0,-1.5
2)确定-根2.轨5,迹-的渐 近线。本例n=4,m=3,故只有
一条 的渐近线。 180
36
K均* 有关。
15
一、 根轨迹法的基本概念(13)
4 -1- 4 根轨迹方程
1、系统闭环特征方程
由闭环传函可得系统闭环特征方程为:
(s)
G(s)
1 G(s)H(s)
1 G(s)H (s) 0
2 、根轨迹方程
当系统有m个开环零点和n个开环极点时,下式称为
根轨迹方程
m
(s z j )
K * j1 n
i 1
j 1
n
n
n
(s si ) sn ( si )sn1 ... (si ) 0
i 1
i 1
i 1
式中,s i 为闭环特征根。
31
二、根轨迹绘制的基本法则(14)
当n m 2 时,特征方程第二项系数与K * 无关,无
论 K * 取何值,开环n个极点之和总是等于闭环特征方程n
自动控制第五章根轨迹法
15
绘制根轨迹的规则
【例5-2】已知负反馈系统的开环传递函数为:
解:(1)根轨迹的分支数和对称性 开环极点分别为: 系统的根轨迹有三条分支 (2)根轨迹的起点与终点 起始于系统的三个开环极点,并趋向于无穷远处
K1 Kb
j Kc
K1
(3)根轨迹的渐近线
Kc K1
16
绘制根轨迹的规则
闭环特征根s1,s2 随着K1值得 改变而变化。
(1) K1= 0:s1 = 0,s2 = 2,是根轨迹的起点,用“”表示。 j K1 (2) 0 < K1<1 :s1 ,s2 均是负实数。 K1 s1 ,s2 。 s1从坐标原点开 始沿负实轴向左移动; s2从(2, K1= 0 K1= 0 K1=1 j0)点开始沿负实轴向右移动。 1 0 2 (3) K1= 1: s1 = s2 = 1,重根。
+
﹣
K s(0.5s+1)
C(s)
式中,K为系统的开环比例系数。 K1 = 2K 称为系统的开环 根轨迹增益。
系统的闭环传递函数为:
K1 ( s) 2 s 2s K1
系统的闭环特征方程为: s2 + 2s + 2K1 = 0
4
一、根轨迹
用解析法求得系统的两个闭环特征根为:
s1,2 1 1 K1
K1
分离角为:
Kb
Kc K1
17
绘制根轨迹的规则
一般情况下,如果根轨迹位于实轴上相邻的开环极点之间, 则在这两个极点之间至少存在一个分离点;同样,如果根 轨迹位于实轴上两个相邻的开环零点之间(其中一个可在 无穷远处),则这两个零点之间至少存在一个汇合点。
自动控制原理第四章根轨迹法

第四章 根轨迹法
第一节 根轨迹与根轨迹方程 根轨迹 系统的某个参数(如开环增益K)由0到∞变化时, 闭环特征根在S平面上运动的轨迹。
例: GK(S)= K/[S(0.5S+1)] = 2K/[S(S+2)] GB(S)= 2K/(S2+2S+2K) 特征方程:S2+2S+2K = 0
-P1)(S-P2)…(S-Pn)
单击此处可添加副标题
当n>m时,只有m条根轨迹趋向于开环零点,还有(n-m)条? m,S→∞,有: (S-Z1)(S-Z2)…(S-Zm) -1 -1 ———————-— = —— = —— P1)(S-P2)…(S-Pn) K* AK 可写成:左边 = 1/Sn-m = 0 当K=∞时,右边 = 0 K=∞(终点)对应于S→∞(趋向无穷远). 即:有(n-m)条根轨迹终止于无穷远。
分解为:
03
例:GK(S)= K/[S(0.05S+1)(0.05S2+0.2S+1)] 试绘制根轨迹。 解: 化成标准形式: GK(S)= 400K/[S(S+20)(S2+4S+20)] = K*/[S(S+20)(S+2+j4)(S+2-j4)] K*=400K——根迹增益 P1=0,P2=-20,P3=-2+j4,P4=-2-j4 n=4,m=0
一点σa。
σa= Zi= Pi
ΣPi-ΣZi = (n-m)σa
σa= (ΣPi-ΣZi)/(n-m)
绘制根轨迹的基本法则
K*(S-Z1)(S-Z2)…(S-Zm)
—————————— = -1 (S-P1)(S-P2)…(S-Pn)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
➢ 当n≠m时,根轨迹存在|n-m|支渐近线,且渐近线与实轴
的夹角为:
k
(2k 1)1800 nm
,
k 0,1,2,,| n m | 1
所有渐近线交于实轴上的一点,其坐标为
n
m
pi zl
i1
l 1
nm
课程:自动控制原理
第4章 根轨迹法
规则4:实轴上的根轨迹
➢ 实轴上的开环零点和开环极点将实轴分为若干段,对其中 任一段,如果其右边实轴上的开环零、极点总数是奇数,
课程:自动控制原理
第4章 根轨迹法
➢ 用根轨迹法分析控制系统时,主要是研究系统的一个可调 参数的变动对系统闭环极点的影响,而最常见的可调参数 就是开环增益K。
➢ 如果令G(s)=KG0(s),显然K的变动只影响幅值条件,不影响 相角条件。也就是说,根轨迹上的所有点都满足相同的相 角条件且不受K值变动的影响,但其幅值与K 值有关。所以, 绘制根轨迹可以这样进行:
零点处根轨迹的走向,稍远一点就不起作用了。
所以,画根轨迹最有用的是规则1~5,如果想得到更精确的 根轨迹图,只有使用Matlab。
那么该段就一定是根轨迹的一部分。
课程:自动控制原理
第4章 根轨迹法
❖ 该规则用相角条件可以证明,设实轴上有一试验点s0。 ➢ 任一对共轭开环零点或共轭极点(如p2,p3),与其对应的
相角(如θ2,θ3)之和均为360°,也就是说任一对共轭开环 零、极点不影响实轴上试验点s0的相角条件。 ➢ 对于在试验点s0左边实轴上的任一开环零、极点,与其对应 的相角(如θ4,φ3)均为0。 ➢ 而试验点s0右边实轴上任一开环零、极点,与其对应的相角 (如θ1,φ1,φ2)均为180°。 所以要满足相角条件,s0右边实轴上的开环零、极点总数必 须是奇数。
规则1:起点和终点
➢ 根轨迹一定开始于开环极点,终止于开环零点。
因为根轨迹是闭环特征方程的根,当K=0时方程的根就是 它的n个开环极点,当K→∞时方程的根就是它的m个开环 零点。
课程:自动控制原理
第4章 根轨迹法
➢ 当n=m时,开始于n个开环极点的n支根轨迹,正好终止于 个开环零点。
➢ 当n>m时,开始于n个开环极点的n支根轨迹,有m支终止 于开环零点,有n-m支终止于无穷远处。 因为,终点就是K→∞的点,要K→∞只有两种情况,一种 是s=zl,另一种是s→∞。这时,无穷远处也称为“无穷远 零点”。
显然,位于实轴上的两个相邻的开环极点之间一定有分离 点,因为任何一条根轨迹不可能开始于一个开环极点终止 于另一个开环极点。同理,位于实轴上的两个相邻的开环 零点之间也一定有分离点。
课程:自动控制原理
第4章 根轨迹法
当然,分离点也可以是复数,两个相邻的开环复极点(或
零点)之间可能有分离点。对实际系统,依据规则1~4基
l 1
i 1
对应的幅值条件为:
相角条件为:
n
( s pi ) K i1
m
(s zl )
l 1
m
n
(s zl ) (s pi ) (2k 1)180
k 1,2,
l 1
i 1
课程:自动控制原理
第4章 根轨迹法
❖ 上述相角条件,即为绘制根轨迹图的依据。具体绘制方法 是:在复平面上选足够多的试验点,对每一个试验点检查 它是否满足相角条件,如果是则该点在根轨迹上,如果不 是则该点不在根轨迹上,最后将在根轨迹上的试验点连接 就得到根轨迹图。
➢ 当n<m时,终止于m个开环零点m支根轨迹,有n支来自n 个开环极点,有m-n支来自无穷远处。 必需指出,实际系统极少有n<m的情况。
课程:自动控制原理
第4章 根轨迹法
规则2:分支数和对称性
➢ 根轨迹一定对称于实轴,并且有max(n,m)支。
因为根轨迹是闭环特征方程的根,无论K如何变化特征方
程始终有max(n,m)个根,即使出现重根,当K从零到无
课程:自动控制原理
第四章 根轨迹法
第4章 根轨迹法
4.1 根轨迹的基本概念 4.2 绘制典型根轨迹 4.3 特殊根轨迹图 4.4 用MATLAB绘制根轨迹图 4.5 控制系统的根轨迹分析
课程:自动控制原理
第4章 根轨迹法
内容提要
➢ 根轨迹法是一种图解法,它是根据系统的开环零
极点分布,用作图的方法简便地确定闭环系统的
课程:自动控制原理
第4章 根轨迹法
❖ 当开环增益K从零到无穷大连续变化时,闭环极点在S平面 (复平面)上移动画出的轨迹图即根轨迹图。从上述根轨迹图 中可以看到:
➢ 当0<K<0.385时三个闭环极点都是负实数;当K>0.385时有 两个闭环极点成为共轭复数。
➢ 只要0<K<6闭环系统一定稳定,一但K值给定,如K=1.2,3 个闭环极点就是3支根轨迹上3个特定点。
课程:自动控制原理
第4章 根轨迹法
4.1 根轨迹的基本概念
1.什么是根轨迹
❖ 考虑图示负反馈控制系统,设其开环传递函数为:
G(s)H(s) K s(s 1)(s 2)
则该系统的闭环特征方程为:
s3 3s2 2s K 0
课程:自动控制原理
第4章 根轨迹法
➢ 当K从零到无穷大连续变化时,闭环极点在S平面(复平面)上 画出的根轨迹如图所示。
以下列4阶系统为例说明,该系统开环传递函数为:
ห้องสมุดไป่ตู้
G(s)H(s)
K(s z1 )
(s p1 )(s p2 )(s p3 )(s p4 )
➢ 先在复平面上标出开环极点p1,p2,p3,p4和开环零点z1。
课程:自动控制原理
第4章 根轨迹法
➢ 再取一试验点s,如果它在根轨迹上就应满足相角条件 : 1 1 2 3 4 (2k 1)180 k 0,1,2,
➢ 2)图解加计算画准确图。此方法不仅繁琐,精度也差,在 实际应用中已逐步淘汰。
➢ 3)计算机绘制精确图,目前主要指用Matlab工具绘制根轨 迹图。它准确快捷,短时间内可以对多个可调参数进行 研究,能够有效地指导设计与调试。
课程:自动控制原理
第4章 根轨迹法
1.开环零极点与相角条件
❖ 以开环增益K为参变量的根轨迹,它是最基本、最常用的 根轨迹,为了便于区别将其称之为‘典型根轨迹’。
1 K (s z1 )(s z2 )....(s zm ) 0 (s p1 )(s p2 )....(s pn )
课程:自动控制原理
第4章 根轨迹法
➢ 以K为参变量的根轨迹上的每一点都必须满足以上方程, 相应地,称之为‘典型根轨迹方程’。
也可以写成
m
n
(s zl ) K (s pi ) 0
本就能确定有无分离点。
➢ 基于分离点是重闭环极点的事实可以证明,分离点的座标λ, 是下列代数方程的解:
n1
m1
i1 pi l1 zl
必须说明的是,方程只是必要条件而非充分条件。也就是
说,方程的解不一定是分离点,是否是分离点还要看其它
规则。
课程:自动控制原理
第4章 根轨迹法
规则7:根轨迹的出射角和入射角
可见,根轨迹可以清晰地描绘闭环极点与开环增益K之间的 关系。
课程:自动控制原理
第4章 根轨迹法
2.根轨迹的基本条件
❖ 考察图示系统,其闭环传递函数为:
Y(s) G(s) R(s) 1 G(s)H(s)
闭环特征方程为:
1 G(s)H(s) 0
➢ 因为根轨迹上的每一点s都是闭环特征方程的根,所以根轨 迹上的每一点都应满足:
G(s)H(s) 1
这就是根轨迹的基本条件。
课程:自动控制原理
第4章 根轨迹法
❖ 满足根轨迹上点的基本条件,又可分别表示为,
幅值条件:
G(s)H(s) 1
相角条件:
G(s)H(s) (2k 1)180 k 0,1,2,
➢ 因为在s平面上,给定了幅值和相角,就可对应一个固定的 点。所以在s平面上,既满足幅值条件又满足相角条件的点 就是根轨迹上的一个点,它对应的s值就是特征方程的一个 根,也就是一个闭环极点。
m
(
j 1
zl
zj)
n
(zl
j 1
p
j
)
jl
课程:自动控制原理
第4章 根轨迹法
❖ 上述规则对绘制根轨迹很有帮助,根据规则1~4就能很快 地画出大致形状,再按规则5求出临界增益K0,这样的根轨 迹图就很有用了,一般称其为概略图。
除非系统阶次很低,否则根据规则6,求解方程求分离点决 非易事;根据规则7,计算出射角和入射角也不简单,并且 出射角和入射角的意义并不大,因为它仅仅反映了开环极、
❖ 根轨迹从某个开环极点出发时的切线与实轴的夹角称为出 射角;根轨迹进入某个开环零点的切线与实轴的夹角称为 入射角。用相角条件不难证明,
➢ 根轨迹从开环极点pi出发的出射角为:
pi
180
m
( pi
j 1
zj)
n
( pi
j 1
p
j
)
ji
➢ 根轨迹进入某个开环零点Zl的入射角为:
zl
180
首先在s平面上找出所有符合相角条件的点,这些点连成 的曲线就是根轨迹。然后反过来,再按幅值条件即可以求 出根轨迹上任意一点所对应的K值。
课程:自动控制原理
第4章 根轨迹法
4.2 绘制典型根轨迹
❖ 现有的绘制根轨迹图的方法分为三类:
➢ 1)画概略图。这种方法适合调试现场的应急分析、项目开 始的粗略分析等不要求很精确的场合。熟悉了根轨迹的 基本规则后,很快就可以画出概略图。
➢ 仍分析前面图示的负反馈系统,设其开环传递函数为:
G(s)H(s) K(s z1)(s z2 )....(s zm ) ,K 0 (s p1 )(s p2 )....(s pn )
