半对数法
抽水试验确定渗透系数的方法及步骤

1.抽水试验资料整理试验期间,对原始资料和表格应及时进行整理。
试验结束后,应进行资料分析、整理,提交抽水试验报告。
单孔抽水试验应提交抽水试验综合成果表,其内容包括:水位和流量过程曲线、水位和流量关系曲线、水位和时间(单对数及双对数)关系曲线、恢复水位与时间关系曲线、抽水成果、水质化验成果、水文地质计算成果、施工技术柱状图、钻孔平面位置图等。
并利用单孔抽水试验资料编绘导水系数分区图。
多孔抽水试验尚应提交抽水试验地下水水位下降漏斗平面图、剖面图。
群孔干扰抽水试验和试验性开采抽水试验还应提交抽水孔和观测孔平面位置图(以水文地质图为底图)、勘察区初始水位等水位线图、水位下降漏斗发展趋势图(编制等水位线图系列)、水位下降漏斗剖面图、水位恢复后的等水位线图、观测孔的S-t、S-lg t曲线[注]、各抽水孔单孔流量和孔组总流量过程曲线等。
注意:(1)要消除区域水位下降值;(2)在基岩地区要消除固体潮的影响;3)傍河抽水要消除河水位变化对抽水孔水位变化的影响。
多孔抽水试验、群孔干扰抽水试验和试验性开采抽水试验均应编写试验小结,其内容包括:试验目的、要求、方法、获得的主要成果及其质量评述和结论。
2. 稳定流抽水试验求参方法求参方法可以采用Dupuit 公式法和Thiem公式法。
(1) 只有抽水孔观测资料时的Dupuit 公式承压完整井:潜水完整井:式中 K——含水层渗透系数 (m/d);Q——抽水井流量 (m3/d);sw——抽水井中水位降深 (m);M——承压含水层厚度 (m);R——影响半径 (m);H——潜水含水层厚度 (m);h——潜水含水层抽水后的厚度 (m);rw——抽水井半径 (m)。
(2) 当有抽水井和观测孔的观测资料时的Dupuit 或Thiem公式式中hw ——抽水井中水柱高度 (m);h1、h2——与抽水井距离为r1和r2处观测孔(井)中水柱高度 (m),分别等于初始水位H0与井中水位降深s之差,h1= H0 –s1;h2= H0 –s2。
半对数公式股票推算
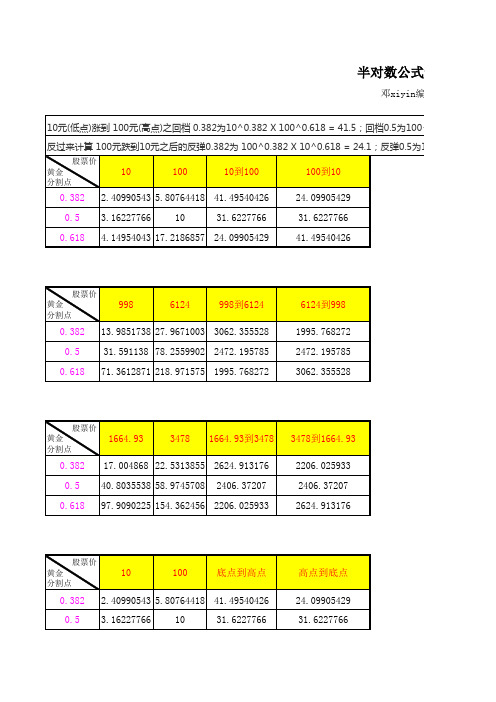
股票价
黄金
1664.93
分割点
3478 1664.93到3478
0.382 17.004868 22.5313855 2624.913176
0.5 40.8035538 58.9745708 2406.37207
0.618 97.9090225 154.362456 2206.025933
备注: 1、X^Y表示X的Y次方
例如:10^0.382表示10的0.382次方 2、黄色区域代表股票价可改动。
股票价 黄金 分割点
0.382
0
0.5
0
0.618
0
ห้องสมุดไป่ตู้
底点到高点 高点到底点
0
0
0
0
0
0
0
0
0
因我叔叔喜欢炒股,我帮忙编辑一个半对数的公式, 只需编辑最低价和最高价即可自动计算。
382次方 。
0.618 4.14954043 17.2186857 24.09905429
41.49540426
对数公式计算
邓xiyin编仅供参考 2012/9/20
档0.5为100^0.5X10^0.5=31.6;回档0.618为10^0.618 X 100^0.382 = 24.1 ;反弹0.5为10^0.5X100^0.5=31.6反弹0.618为100^0.618 X 10^0.382 = 41.5
半对数公式计算
邓xiyin编仅供参考 2012/9/
10元(低点)涨到 100元(高点)之回档 0.382为10^0.382 X 100^0.618 = 41.5;回档0.5为100^0.5X10^0.5=31
抽水试验资料整理及参数确定方法

抽水试验资料整理及参数确定方法1.抽水试验资料整理试验期间,对原始资料和表格应及时进行整理。
试验结束后,应进行资料分析、整理,提交抽水试验报告。
单孔抽水试验应提交抽水试验综合成果表,其内容包括:水位和流量过程曲线、水位和流量关系曲线、水位和时间(单对数及双对数)关系曲线、恢复水位与时间关系曲线、抽水成果、水质化验成果、水文地质计算成果、施工技术柱状图、钻孔平面位置图等。
并利用单孔抽水试验资料编绘导水系数分区图。
多孔抽水试验尚应提交抽水试验地下水水位下降漏斗平面图、剖面图。
群孔干扰抽水试验和试验性开采抽水试验还应提交抽水孔和观测孔平面位置图(以水文地质图为底图)、勘察区初始水位等水位线图、水位下降漏斗发展趋势图(编制等水位线图系列)、水位下降漏斗剖面图、水位恢复后的等水位线图、观测孔的S-t、S-lg t曲线[注]、各抽水孔单孔流量和孔组总流量过程曲线等。
注意:(1)要消除区域水位下降值;(2)在基岩地区要消除固体潮的影响;3)傍河抽水要消除河水位变化对抽水孔水位变化的影响。
多孔抽水试验、群孔干扰抽水试验和试验性开采抽水试验均应编写试验小结,其内容包括:试验目的、要求、方法、获得的主要成果及其质量评述和结论。
2. 稳定流抽水试验求参方法求参方法可以采用Dupuit 公式法和Thiem公式法。
(1) 只有抽水孔观测资料时的Dupuit 公式承压完整井:潜水完整井:式中K——含水层渗透系数(m/d);Q——抽水井流量(m3/d);s w——抽水井中水位降深(m);M——承压含水层厚度(m);R——影响半径(m);H——潜水含水层厚度(m);h——潜水含水层抽水后的厚度(m);r w——抽水井半径(m)。
(2) 当有抽水井和观测孔的观测资料时的Dupuit 或Thiem公式式中h w ——抽水井中水柱高度(m);h1、h2——与抽水井距离为r1和r2处观测孔(井)中水柱高度(m),分别等于初始水位H0与井中水位降深s之差,h1= H0 –s1;h2= H0 –s2。
半对数计算精编版

半对数计算一、何谓股价三分线▲我们常计算回档(反弹)1/3、0.382、1/2、0.618,其实1/3与0.382属同层级,意谓强势整理(弱势反弹),乃最有机会创高(破底)之表征。
1/2中线则是最普遍运用的支撑或压力之观测点,因为这里是回档或反弹的成本均衡处,稳定的涨势或跌是常藉1/2中线之转折继续维系其多空步伐。
至于0.618乃回檔的『最后防线』及反弹的『乾坤挪移』所在,前者跌破,防回档转回跌,后者突破可促反弹转回升,这一关的重要性关乎原始趋势之转变与否。
◆问题来了!没人规定股价的高低点要落在三分线位置,若视之为『随机』落在任何位置皆可能,重要的是据美国分析界学者之长期统计,落在三分线附近之机率远大于其它位置,足见其存在的惯性意义。
二、为什么要用半对数计算▲很多人早就会自行计算所谓的回档(反弹)1/3、1/2及黄金切割率,久而久之却懒得算了;原因是算不出『准头』!何以艾略特主张要用『半对数』?例:10→100的中心点在哪? 小学生也知道(10 + 100 ) / 2 = 55,但是,股价的运算~ √10 X 100 = 31.6。
半对数乃一门运用数学,并适用于股市这门投资学。
◆原理:拿一百万元买一档10元的股票,涨到31.6元增值为316万;又,拿一百万元买足一档31.6元的股票,涨到100元同样增值为316万。
可见31.6才是10←→100的涨跌『成本中心』位置;若说线图为人性之轨迹,那么『惯性』透过半对数计算才得知最敏感的表征处。
进而推演出公式:10→100回檔1/3~ 100.333 X 1000.666= 46.2;100 →10反弹1/3~ 1000.333 X 100.666= 21.5。
所以说,一定要用工程用计算器才算得出来。
三、如何『取样』来加强计算的可信度?▲半对数计算必须先有『背景取样』,因为我们是藉由前一上涨波来测量回档支撑,由前一下跌波来测量反弹压力;但所谓的『前一波』可长可短,且走势不见得如想象中单纯,是故,取样的准则应力求:一、较佳的线性轨道(走势太曲折则不佳);二、较符合波浪循环之原则。
抽水试验确定渗透系数的方法及步骤

抽水试验确定渗透系数的方法及步调之欧侯瑞魂创作 1.抽水试验资料整理试验期间,对原始资料和表格应及时进行整理。
试验结束后,应进行资料分析、整理,提交抽水试验陈述。
单孔抽水试验应提交抽水试验综合成果表,其内容包含:水位和流量过程曲线、水位和流量关系曲线、水位和时间(单对数及双对数)关系曲线、恢复水位与时间关系曲线、抽水成果、水质化验成果、水文地质计算成果、施工技术柱状图、钻孔平面位置图等。
并利用单孔抽水试验资料编绘导水系数分区图。
多孔抽水试验尚应提交抽水试验地下水水位下降漏斗平面图、剖面图。
群孔干扰抽水试验和试验性开采抽水试验还应提交抽水孔和观测孔平面位置图(以水文地质图为底图)、勘察区初始水位等水位线图、水位下降漏斗发展趋势图(编制等水位线图系列)、水位下降漏斗剖面图、水位恢复后的等水位线图、观测孔的S-t、S-lg t曲线[注]、各抽水孔单孔流量和孔组总流量过程曲线等。
注意:(1)要消除区域水位下降值;(2)在基岩地区要消除固体潮的影响;3)傍河抽水要消除河水位变更对抽水孔水位变更的影响。
多孔抽水试验、群孔干扰抽水试验和试验性开采抽水试验均应编写试验小结,其内容包含:试验目的、要求、方法、获得的主要成果及其质量评述和结论。
2. 稳定流抽水试验求参方法求参方法可以采取Dupuit 公式法和Thiem公式法。
(1) 只有抽水孔观测资料时的Dupuit 公式承压完整井:潜水完整井:式中 K——含水层渗透系数 (m/d);Q——抽水井流量 (m3/d);sw——抽水井中水位降深 (m);M——承压含水层厚度 (m);R——影响半径 (m);H——潜水含水层厚度 (m);h——潜水含水层抽水后的厚度 (m);rw——抽水井半径 (m)。
(2) 当有抽水井和观测孔的观测资料时的Dupuit 或Thiem公式式中hw ——抽水井中水柱高度 (m);h1、h2——与抽水井距离为r1和r2处观测孔(井)中水柱高度(m),分别等于初始水位H0与井中水位降深s之差,h1= H0 –s1;h2= H0 –s2。
半对数模型中的扩大效应与缩小效应

半对数模型中的扩大效应与缩小效应在经济学和统计学中,半对数模型是一种常用的回归分析方法,用于研究自变量对因变量的影响程度。
在这种模型中,因变量取对数,而自变量可以是对数或者非对数,半对数模型常用于探究变量之间的非线性关系。
在半对数模型中,我们经常关注的一个重要概念就是扩大效应与缩小效应。
扩大效应与缩小效应是指在半对数模型中,自变量的增加对因变量的影响。
通俗地讲,扩大效应表示自变量的增加会加大对因变量的影响,而缩小效应则表示自变量的增加会减小对因变量的影响。
对于经济学家和政策制定者来说,了解自变量的扩大效应和缩小效应对于制定政策和预测效果至关重要。
在半对数模型中,自变量的扩大效应和缩小效应是通过回归系数的解释来得到的。
具体来说,如果一个自变量的回归系数为正,则增加这个自变量会导致因变量的增加,这就是扩大效应;反之,如果回归系数为负,则增加自变量会导致因变量的减小,这就是缩小效应。
而在实际研究中,我们常常需要对这些扩大效应和缩小效应进行进一步分析,以便更好地理解自变量的影响。
在经济学研究中,半对数模型的扩大效应和缩小效应常常被用来分析政策的效果。
在一项关于最低工资政策的研究中,经济学家可能会使用半对数模型来研究提高最低工资对就业的影响。
通过分析最低工资的扩大效应和缩小效应,研究者可以更好地评估提高最低工资的政策对就业的影响,以及对经济整体的影响。
了解最低工资的扩大效应和缩小效应还可以帮助政策制定者更好地调整最低工资标准,以达到更好的就业和经济效果。
除了应用于政策研究外,半对数模型的扩大效应和缩小效应还可以用于市场营销和消费行为的研究。
在研究产品价格对销量的影响时,我们可以使用半对数模型来分析价格的扩大效应和缩小效应。
通过了解价格的扩大效应和缩小效应,企业可以更好地制定定价策略,以实现最大化利润。
消费者行为研究中也可以使用半对数模型来分析广告投放对消费者购买行为的影响,从而更好地了解广告的扩大效应和缩小效应。
半对数计算公式

半对数计算公式半对数计算一、何谓股价三分线▲我们常计算回档(反弹)1/3、0.382、1/2、0.618,其实1/3与0.382属同层级,意谓强势整理(弱势反弹),乃最有机会创高(破底)之表征。
1/2中线则是最普遍运用的支撑或压力之观测点,因为这里是回档或反弹的成本均衡处,稳定的涨势或跌是常藉1/2中线之转折继续维系其多空步伐。
至于0.618乃回檔的『最后防线』及反弹的『乾坤挪移』所在,前者跌破,防回档转回跌,后者突破可促反弹转回升,这一关的重要性关乎原始趋势之转变与否。
◆问题来了!没人规定股价的高低点要落在三分线位置,若视之为『随机』落在任何位置皆可能,重要的是据美国分析界学者之长期统计,落在三分线附近之机率远大于其它位置,足见其存在的惯性意义。
二、为什么要用半对数计算▲很多人早就会自行计算所谓的回档(反弹)1/3、1/2及黄金切割率,久而久之却懒得算了;原因是算不出『准头』!何以艾略特主张要用『半对数』?例:10 → 100 的中心点在哪 ? 小学生也知道 ( 10 + 100 ) / 2 = 55,但是,股价的运算~ √10 X100 = 31.6。
半对数乃一门运用数学,并适用于股市这门投资学。
◆原理:拿一百万元买一档10元的股票,涨到31.6元增值为316万;又,拿一百万元买足一档31.6元的股票,涨到100元同样增值为316万。
可见31.6才是10←→100的涨跌『成本中心』位置;若说线图为人性之轨迹,那么『惯性』透过半对数计算才得知最敏感的表征处。
进而推演出公式:10 → 100回檔1/3 ~ 100.333 X 1000.666= 46.2;100 → 10 反弹 1/3 ~1000.333 X 100.666= 21.5。
所以说,一定要用工程用计算器才算得出来。
三、如何『取样』来加强计算的可信度 ?▲半对数计算必须先有『背景取样』,因为我们是藉由前一上涨波来测量回档支撑,由前一下跌波来测量反弹压力;但所谓的『前一波』可长可短,且走势不见得如想象中单纯,是故,取样的准则应力求:一、较佳的线性轨道(走势太曲折则不佳);二、较符合波浪循环之原则。
半对数法

y y y e
t T
t ln y y ln y T1
• 以 作为纵坐标,t作为横坐标,得 一条直线。直线与纵坐标交于A,直线斜率为-1/T ln y y
y t y Ae
T1
Be
T2
Ce
ห้องสมุดไป่ตู้T3
• 在对象响应的响应时间上, 依次量出 y y • 的数值分别点在半对数坐标上,连接各点 得线1,线1不是一条直线,但是时间t很大 时,即在线1的后半部分近似是一条直线。 因 t t T T1 T2 T3 ,当t很大时, T2 Be • 和Ce 衰 t Ae 减后的数值对应于T 衰减后的数值可以 忽略不计
3
1
• 式(1)可近似表示为 • t • 或 y y Ae T1 • • 上式两边取对数后得
y y Ae
t T1
•
t ln y y ln A T1
• 这与一阶惯性环节一样。基于这样的假设, 就可将线1的直线段延长相交于纵坐标 (t=0)点A,得到线2,直线2的斜率 1 T 为 ,由此求得直线2数值0.368A所对应 的时间即为对象第一时间常数
• 上式即为线5的直线方程式,直线与总坐标 交于C点,直线斜率为 ,则在直线5数 1 T 值等于0.368C时所对应的时间即为第三个 时间常数 ,这样就求得了三阶对象的 T3 传递函数
3
• 两边取对数:
t ln y y ln A T1
• 两边取对数:
Tt Tt t ln Be 2 Ae 1 y y ln C T3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
T1
• 当t较小时,曲线1不是直线,主要是由于t 较小时, 等的影响不能忽略不计,因而 Be 在求取时必须同时考虑。如果我们将线2的 数值减去同一时间下线1的数值(是真数不 是对数),得线3。当t较大时,线3后面部 分近似一直线。
t T2
• 这是因t较大时, t 衰减后的数值对于 T3 • 和 t Ce 衰减后的数值可以忽略不计, t Ae T Be T 则式(1)可写成
2
1
y y Ae
t T1
Bey y Be
t T2
• 两边取对数后得
Tt t ln Ae 1 y y ln B T2 • 这是一直线方程式,式中 t 即为直线2, • 即为曲线1,两者之差即为线3。同前一样,将线3 Ae T1 y y 直线段延长交于纵坐标B点(t=0),得线4,其斜率 1 为 ,
• 上式即为线5的直线方程式,直线与总坐标 交于C点,直线斜率为 ,则在直线5数 1 T 值等于0.368C时所对应的时间即为第三个 时间常数 ,这样就求得了三阶对象的 T3 传递函数
3
• 两边取对数:
t ln y y ln A T1
• 两边取对数:
Tt Tt t ln Be 2 Ae 1 y y ln C T3
半对数法
图1.21 用半对数法求一阶对象时间常数
K G s Ts 1 t y t K u 1 e T
t y t y 1 e T
y y y e
t T
t ln y y ln y T1
T2
• 则在直线4的数值等于0.368B所对应的时间,即为对象的 第二个时间常数 T2
• 线3还不是直线,继续用上法将线4之值减 去同一时间下线3之值,得线5。由图看出, 线5是一根近似直线,说明对象是一个三阶 惯性环节。由式(1)仿上作法可得
Tt Tt t 2 1 ln Be Ae y y ln C T3
y t y Ae
T1
Be
T2
Ce
T3
• 在对象响应的响应时间上, 依次量出 y y • 的数值分别点在半对数坐标上,连接各点 得线1,线1不是一条直线,但是时间t很大 时,即在线1的后半部分近似是一条直线。 因 t t T T1 T2 T3 ,当t很大时, T2 Be • 和Ce 衰 t Ae 减后的数值对应于T 衰减后的数值可以 忽略不计
• 以 作为纵坐标,t作为横坐标,得 一条直线。直线与纵坐标交于A,直线斜率为-1/T ln y y
tg
• 当 • 则t T
时
1 ln A ln M T 0t ln A ln M t
ln A ln M 1
M 0.368 A • 由此可以得到直线数值为0.368A时的时间,即为对 象的时间常数T,亦即MN=T
• 设三阶对象的传递函数为:
• 其阶跃响应是:
图1.22 三阶对象时间常数的求解 (a)三阶对象阶跃响应;(b)时间常数T1、T2、T3的求解
• 设已知一个三阶惯性环节的传递函数为
K G s T1s 1T2 s 1T3 s 1
• 且 ,则对象的阶跃响应可表示为 • T1 T2 T3 t t t • (1)
3
1
• 式(1)可近似表示为 • t • 或 y y Ae T1 • • 上式两边取对数后得
y y Ae
t T1
•
t ln y y ln A T1
• 这与一阶惯性环节一样。基于这样的假设, 就可将线1的直线段延长相交于纵坐标 (t=0)点A,得到线2,直线2的斜率 1 T 为 ,由此求得直线2数值0.368A所对应 的时间即为对象第一时间常数
