东南大学高等数学A(上册)数学实验报告

合集下载

东南大学高等数学a教材答案解析

东南大学高等数学a教材答案解析高等数学A是一门重要的数学课程，它对于学生提高数学理论水平和解决实际问题具有重要意义。

然而，在学习高等数学A过程中，很多学生都会遇到一些难题，需要教材答案解析的帮助。

本文将根据东南大学高等数学A教材，对一些典型题目进行解析，帮助学生更好地理解和掌握高等数学A的知识。

第一章: 函数与极限1.1. 函数的概念与性质在这一章中，我们首先介绍了函数的概念与性质。

函数是一种映射关系，它将一个自变量的值映射到一个因变量的值。

函数的性质包括定义域、值域、单调性、奇偶性等。

通过掌握这些性质，我们可以更好地理解函数的特点与行为。

1.2. 三角函数与函数的图像三角函数是高等数学A中的重要内容。

在这一小节中，我们重点介绍了正弦函数、余弦函数和正切函数的定义、性质以及它们的图像。

掌握三角函数的图像可以帮助我们更好地理解其周期性、振幅等特点。

1.3. 函数的极限与连续性函数的极限是高等数学A中的关键概念之一。

我们在这一小节中通过一些例子详细解析了函数极限的定义、性质以及计算方法。

同时，我们还介绍了函数的连续性与间断点的概念，帮助学生理解函数在某一点是否具有连续性。

1.4. 函数的导数与微分函数的导数与微分是高等数学A中的重要内容。

我们在这一小节中详细解析了导数的定义、计算方法以及导数的几何意义。

同时，我们还介绍了微分的概念与计算方法，帮助学生理解函数的变化率与微分之间的关系。

第二章：定积分与不定积分2.1. 定积分的概念与性质定积分是高等数学A中的重要内容。

在这一章中，我们首先介绍了定积分的概念与性质，包括定积分的定义、区间的选取以及定积分的性质。

帮助学生掌握定积分的含义及其计算方法。

2.2. 定积分的计算方法在这一小节中，我们重点介绍了定积分的计算方法。

通过具体的例子和详细的步骤，帮助学生理解和掌握定积分的计算过程，包括换元法、分部积分法等。

2.3. 不定积分的概念与计算方法不定积分是定积分的逆运算。

大一高数实验报告

a[0] +Sum [ a[k]*Cos[kx] + b[k]*Sin[kx], {k,1,n}]; 2
g1=Plot[f[x],{x,-2Pi,2Pi},PlotStyle->RGBColor[0,0,1], DisplayFunction->Identity]; m=18; For[i=1, i ≤m, i+=2, g2=Plot[Evaluate[s[x,i]], {x,-2Pi,2Pi}, DisplayFunction->Identity]; Show[g1,g2, DisplayFunction->$ DisplayFunction]]
四、程序运行结果
1 0.75 Z 0.5 0.25 0 -1 -0.5 0 X 0.5 1 -1 -0.5 0 1 0.5 Y
1
PDF 文件使用 "pdfFactory Pro" 试用版本创建
东南大学实验报告
五、结果的讨论和分析
曲面 x 2 + z = 1, y 2 + z = 1 ，z=0 的参数方程分别为：x=u，y=v，z=-u +1；
四、程序设计 ParametricPlot3D[{r*Cos[u],r*Sin[u], r 2 − 1 },{u,0,2*Pi}, {r,1, 2 }, PlotPoints->30] 五、程序运行结果
1 0.75 0.5 0.25 0 0 -1 0 1 -1
1
六、结果的讨论和分析
由解析几何知识，曲面 z = 0, z = 1 与 z 2 + 1 = x 2 + y 2 所围成立体是一个单叶双曲面介于平面
,
实验四一、实验题目：演示在 yOz 平面内， z=2y 绕 z 轴旋转一周所得曲面方程的过程。二、实验目的和意义

高数实验报告doc(两篇)

高数实验报告引言：高等数学是大学理工科专业中必修的一门基础课程，通过实验可以帮助学生更好地理解和应用数学知识。

本实验报告旨在介绍高等数学实验的目的、原理和实验结果，以及对实验过程的详细阐述。

通过实验，学生可以深入了解高等数学的概念和方法，并提高其数学建模和问题解决的能力。

概述：一、数列与数学归纳法：1.数列的概念和性质2.等差数列和等比数列的求和公式3.斐波那契数列4.数学归纳法的原理和应用5.数学归纳法在证明数学命题中的应用二、函数与导数：1.函数的概念和分类2.复合函数的求导法则3.高阶导数与泰勒展开4.特殊函数的导数求解5.函数与导数在实际问题中的应用三、不定积分与定积分：1.不定积分的定义和性质2.基本初等函数的不定积分3.分部积分和换元积分法4.定积分的概念和性质5.定积分在几何、物理等领域中的应用四、微分方程：1.微分方程的基本概念和分类2.一阶常微分方程的解法3.二阶常微分方程的解法4.高阶常微分方程与常系数线性齐次微分方程5.微分方程在科学和工程领域的应用五、级数与幂级数：1.级数的概念和性质2.级数的收敛与发散3.幂级数的收敛域4.幂级数的求和与展开5.幂级数在数学分析中的应用总结：通过本次高等数学实验，我们对数列与数学归纳法、函数与导数、不定积分与定积分、微分方程以及级数与幂级数等知识进行了深入了解和实践。

实验过程中，我们运用数学原理和方法解决了一系列数学问题，并将理论知识应用到实际问题解决中。

通过实验，我们不仅加深了对高等数学的理解和掌握，也提高了自己的数学建模和问题解决能力。

这次实验为我们的数学学习和应用提供了宝贵的经验和机会。

引言概述本文是一篇关于高数实验的报告，主要探讨了高数实验的意义、目的、实验方法以及实验结果和分析等内容。

高数实验是大学高数课程的重要组成部分，通过实验能够帮助学生更好地理解和应用数学知识，提高解决实际问题的能力。

本文将从实验目的、实验方法和实验结果三个方面进行详细阐述，并对实验进行总结与分析。

(整理)东大高数实验报告.

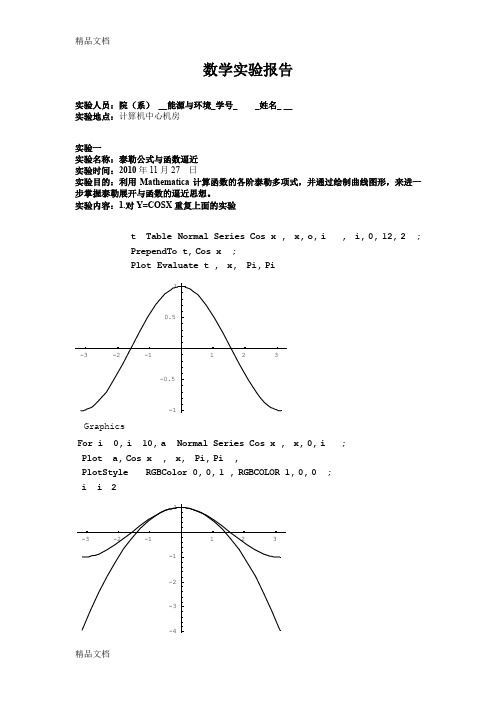
数学实验报告实验人员：院（系）__能源与环境_学号_ _姓名_ __实验地点：计算机中心机房实验一实验名称：泰勒公式与函数逼近实验时间：2010年11月27 日实验目的：利用Mathematica计算函数的各阶泰勒多项式，并通过绘制曲线图形，来进一步掌握泰勒展开与函数的逼近思想。

实验内容：1.对Y=COSX重复上面的实验t Table Normal Series Cos x ,x,o,i ,i,0,12,2;PrependTo t,Cos x;Plot Evaluate t ,x,Pi,PiGraphicsFor i0,i10,a Normal Series Cos x,x,0,i;Plot a,Cos x,x,Pi,Pi,PlotStyle RGBColor0,0,1,RGBCOLOR1,0,0;i i2For i6,i16,a Normal Series Cos x,x,0,i; Plot a,Cos x,x,2Pi,2Pi,PlotStyle RGBColor0,0,1,RGBColor1,0,0;i i22.作出函数Y=ln(cosx^2+sinx) (-π/4, π/4)的函数图形和泰勒展开式图形，选取不同的X0和n，并进行比较。

y x_:Log Cos x^2Sin x;Plot y x ,x,Pi4,Pi 4Graphicsclear;y x_:Log Cos x^2Sin x;t Table Normal Series y x,x,0,i,i,0,10,2;PrependTo t;Plot Evaluate t,x,Pi4,Pi4PrependTo::argr:PrependTo calledwith1argument;2arguments are expected.Graphicsclear;y x_:Log Cos x^2Sin x;t1Table Normal Series y x ,x,3,10;PrependTo t1;Plott1,x,Pi 4,Pi 4-0.75-0.5-0.250.250.50.75-1.41013-1.21013-11013-81012-61012-41012-21012Graphics clear;y x_:Log Cos x^2Sin x ;t1Table Normal Series y x ,x,5,10;PrependTo t1;Plott1,x,Pi 4,Pi 4-0.75-0.5-0.250.250.50.75-1.21025-11025-81024-61024-41024-21024Graphics实验心得：利用Mathematica 计算函数的各阶泰勒多项式，并通过绘制曲线图形，进一步掌握泰勒展开与函数的逼近思想。

东大2024高数实验报告(二)2024

东大2024高数实验报告（二）引言概述：本文是关于东大2024高数实验报告（二）的文档，旨在详细介绍实验过程、实验结果以及相关分析。

本次实验主要涉及高数实验的第二部分，通过理论和实际操作，探索了相关概念和计算方法。

正文：一、实验目的\t1.1 掌握函数的空间曲线的绘制方法；\t1.2 理解函数的周期性和奇偶性；\t1.3 学习利用反函数求解方程；\t1.4 进一步熟悉函数的极限和连续性；\t1.5 学习使用泰勒级数近似计算函数值。

二、实验方法\t2.1 准备实验仪器和材料；\t2.2 绘制函数的空间曲线；\t2.3 分析函数的周期性和奇偶性；\t2.4 求解方程的反函数；\t2.5 进行函数极限和连续性的实验；\t2.6 使用泰勒级数近似计算函数值。

三、实验结果\t3.1 绘制了不同函数的空间曲线并进行了详细分析；\t3.2 确定了函数的周期性和奇偶性，得出相应结论；\t3.3 成功求解了多个方程的反函数，并验证了其正确性；\t3.4 实验得出了函数的极限和连续性的结果，并与理论知识进行了比较；\t3.5 利用泰勒级数近似计算了多个函数值，并与准确值进行了对比。

四、分析和讨论\t4.1 通过绘制空间曲线，我们更直观地理解了函数的变化规律；\t4.2 通过分析周期性和奇偶性，我们对函数的对称性有了更深入的认识；\t4.3 反函数的求解为我们解方程提供了另一种方法，提高了问题的解决效率；\t4.4 实验结果与理论知识的一致性表明，我们掌握了函数的极限和连续性的基本概念；\t4.5 泰勒级数的使用使我们更方便地近似计算各种函数值，提高了计算的准确性。

五、总结\t通过本次实验，我们进一步学习和巩固了高数实验的相关知识和技能。

通过实践，我们熟练掌握了函数的空间曲线绘制方法，理解并应用了周期性和奇偶性的概念，掌握了反函数的求解方法，加深了对函数的极限和连续性的理解，学会了使用泰勒级数近似计算函数值。

这些实验结果对于我们今后的学习和应用中都具有重要的指导作用。

东南大学高数A下实验报告

高数实验报告学号：姓名：数学实验一一、实验题目：（实验习题7-3）观察二次曲面族kxy y x z ++=22的图形。

特别注意确定k 的这样一些值，当k 经过这些值时，曲面从一种类型变成了另一种类型。

二、实验目的和意义1. 学会利用Mathematica 软件绘制三维图形来观察空间曲线和空间曲线图形的特点。

2. 学会通过表达式辨别不同类型的曲线。

三、程序设计这里为了更好地分辨出曲线的类型，我们采用题目中曲线的参数方程来画图，即t t kr r z sin cos 22+=输入代码： ParametricPlot3D[{r*Cos[t]，r*Sin[t],r^2+ k*r^2*Cos[t]*Sin[t]}, {t, 0, 2*Pi}, {r, 0, 1}，PlotPoints -> 30] 式中k 选择不同的值：-4到4的整数带入。

四、程序运行结果k=4：k=3：k=2：k=1:k=0:k=-1:k=-2:k=-3:k=-4:五、结果的讨论和分析k取不同值，得到不同的图形。

我们发现，当|k|<2时，曲面为椭圆抛物面；当|k|=2时，曲面为抛物柱面；当|k|>2时，曲面为双曲抛物面。

数学实验二一、实验题目一种合金在某种添加剂的不同浓度下进行实验，得到如下数据：2+y+=cxabx法确定系数a,b,c，并求出拟合曲线二、实验目的和意义1.练习使用mathematic进行最小二乘法的计算2.使用计算机模拟，进行函数的逼近三、程序设计x={10.0,15.0,20.0,25.0,30.0};y={27.0,26.8,26.5,26.3,26.1};xy=Table[{x[[i]],y[[i]]},{i,1,5}];q[a_,b_,c_]:=Sum[(a+b*x[[i]]+c*x[[i]]*x[[i]]-y[[i]])^2,{i,1 ,5}];Solve[{D[q[a,b,c],a]0,D[q[a,b,c],b]0,D[q[a,b,c],c]0}, {a,b,c}]A={a,b,c}/.%;a=A[[1,1]];b=A[[1,2]];c=A[[1,3]];data=Table[{x[[i]],y[[i]]},{i,1,5}];t1=ListPlot[data,PlotStyle PointSize[0.02],DisplayFunction Identity];f[x_]:=a+b*x+c*x*x;t2=Plot[f[x],{x,0,30},DisplayFunction Identity];Show[t1,t2,DisplayFunction$DisplayFunction]四、程序运行结果{{a 27.56,b -0.0574286,c0.000285714}}五、结果的讨论和分析从图中可以看出，使用最小二乘法可以快捷地确定经验公式的系数，并且得出的拟合曲线可以很好地逼近实验数据。

东南大学高等数学A教材答案

东南大学高等数学A教材答案第一章导数与微分1. 导数的定义与基本公式在本章中，我们将学习导数的定义以及一些基本公式。

导数定义为函数在某一点处的变化率。

而导数的计算公式包括常见函数的导数公式、复合函数求导法则、以及三角函数的导数等。

通过掌握这些基本公式，我们可以更加方便地求解函数的导数。

2. 高阶导数与隐函数求导除了一阶导数外，我们还可以计算高阶导数，即二阶导数、三阶导数等。

高阶导数的计算需要使用基本公式并进行多次求导。

另外，本章还将介绍隐函数求导的方法，即在隐式函数表达式中，如何求取其导数。

3. 函数的极值与最值通过求解函数的导数，我们可以得到函数的极值点。

对于极值点，我们可以使用导数的符号表来判断其是极大值还是极小值。

而对于闭区间上的函数，其最大值和最小值可以通过求解导数和边界点得到。

第二章定积分与不定积分1. 定积分的概念与性质在本章中，我们将介绍定积分的概念与性质。

定积分是函数的一个重要性质，表示曲线与 x 轴之间的面积。

而求解定积分的方法通常包括几何法和解析法。

此外，定积分还具有线性性和积分中值定理等性质。

2. 不定积分的概念与基本公式不定积分是定积分的逆运算，表示函数的原函数。

通过求解不定积分，我们可以还原出函数的原貌。

而不定积分的基本公式包括常见函数的积分公式、分部积分法、以及换元积分法等。

3. 牛顿—莱布尼茨公式与定积分的应用牛顿—莱布尼茨公式是计算定积分的重要工具，它将定积分与原函数联系在一起。

除了牛顿—莱布尼茨公式，本章还将介绍定积分在几何学、物理学以及金融学等领域的应用。

第三章微分方程1. 微分方程的基本概念与解法微分方程是描述函数与其导数之间关系的方程。

本章将详细介绍微分方程的基本概念，包括一阶和二阶微分方程，以及线性和非线性微分方程。

同时，我们也将给出一些常见微分方程的解法。

2. 可分离变量与齐次方程可分离变量和齐次方程是解决一阶微分方程的两种常见方法。

可分离变量法是通过将方程两边进行变量分离，再进行积分求解。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高等数学数学实验报告
实验人员：院（系）：计算机学号：姓名：成绩_________ 实验时间：2010年12月25日 9：00-11:30
实验一：观察数列的极限
一、实验题目一
根据上面的实验步骤，通过作图，观察重要极限：
e n =∞→n
)n
1 + (1lim 二、实验目的和意义
从点图上看出数列的收敛性，以及近似地观察出数列的收敛值；通过编程
可以输出数列的任意多项值，以此来得到数列的收敛性。

通过此实验对数列极限概念的理解形象化、具体化。

三、计算公式四、程序设计
五、程序运行结果
六、结果的讨论和分析
从点图可以看出，该数列是收敛的，并且收敛值在2.7左右，所以可以估计出e 的近似值为2.7
实验二：一元函数图形及其性态
一、实验题目二
制作函数y=sin cx的图形动画，并观察参数c对函数图形的影响
二、实验目的和意义
通过作图形动画，观察参数c对函数性态（周期，最值，奇偶，凹凸）的影响，从而对函数的理解形象化、具体化。

三、计算公式
sin(-x)=sin(x)
sin(x+2π)=sin(x)
sin(x+π)=-sin(x)
四、程序设计
五、程序运行结果
六、结果的讨论和分析
当参数|c|越大，函数的周期越小，并且符合T=2π/|c|;
参数c 的变化并不影响函数的最值，奇偶性（当p=0时，函数是既奇又偶函数），和凹凸性。

参数c 的正负决定函数是在某一确定周期内的正负值
实验三：泰勒公式和函数逼近
一、实验题目三
作出函数sinx)ln(cosx y 2
+= )4
4
(-π
π
≤
≤x 函数图形和泰勒展开式
（选取不同的0x 和n 值）图形，并将图形进行比较.
二、实验目的和意义
下面我们利用Mathematica 计算函数)(x f 的各阶泰勒多项式，并通过绘制曲线图形，来进一步掌握泰勒展开与函数逼近的思想。

三、计算公式
四、程序设计
0x =0时
）（n k n
k k x x o x x k x f x f x f ||)(!
)
()()(001
0)(0-+-+=∑
=
0x =2
时
0x =4时
0x =6时
五、程序运行结果
六、结果的讨论和分析
通过上面六幅图，从图中可以观察到泰勒多项式与函数图形的重合与分离情况，显然在]4.0,4.0[ππ-范围内，当阶数为4-6时两个函数的图形已经基本上吻合了，。