可展曲面的展开
机械制图-展开

组成,求它的展开图,就是要求出属于立体
表面的所有多边形的实形,并将他们依次连 续地画在一个平面上。
三棱锥的表面展开图
s’ SB SA
Z
SC
A
C
a’
b’
c’ c
H面投影
A S
B
s
a A
b
漏斗的表面展开图
a’
A B SA A
1’
Ⅱ
Ⅰ Ⅳ
D
s’ C c
3 4
Ⅲ S
Ⅲ
C
b s
2 1
d
a
二.可展曲面立体的表面展开
曲面上相邻两素线为相交或平行的两直线, 由于相邻两素线构成一平面,故为可展曲面。 如柱面展开时,先在柱面上引若干条互相 平行的素线,然后将相邻两素线间的表面近似 地作为一个四边形平面来画展开图,最后将各 素线的端点连成直线或光滑曲线。
截头圆柱面的展开图
d
不可展曲面立体表面的近似展开
曲面相邻两素线为交叉两直线或为曲线时, 不能构成一平面,故为不可展开的曲面。 不可展曲面只能采用近似展开,其方法是 将曲面分成若干较小部分(同一曲面可有不 同的分法),使每一部分的形状接近于一可 展曲面,画出其展开图。 如球面的展开,可按柱面或锥面展开,也 可把两种方法结合起来。
展开,而圆锥面又可分成若干三角形。
变形接头的展开
b’
实长
a’
c2 b a:
在可展曲面中,由弦代弧作图展开,展开是 近似的,但不称为近似展开,而称为展开的近 似结果,此种结果的误差是可以消除的(当 n时); 在不可展曲面中,近似展开的误差是不可以 消除的。所以展开的近似结果和近似展开是不 同的,要加以区别。
按立体表面的真实形状和大小,依次连续 地摊平在一个平面上,称为立体的表面展开。 展开所得的图形称为展开图。(放样图)
曲面和钣金的展开问题

经常有朋友提到某钣金件或某曲面如何展开的问题,可惜其中大部分实例却往往又是不可展开的。
因此,我想在此谈谈自己对展开问题的看法。
钣金的展开与曲面的展开,就其本质来说是同一个问题。
钣金件的中心层是一个曲面,如果此曲面可展开,那么该钣金件就是可展开的。
因此在下面主要讲一下曲面的展开问题。
根据自己工作的经验,在这里给出一个“曲面展开”的粗略含义:当一个曲面与一个平面图形有点点对应的关系,并且曲面上任一微段的两个端点与平面上对应的两点距离相等,则称此平面为该曲面的一个展开(为了便于说明问题,避免问题的复杂化,上面的含义不是一个严格意义上的定义,其中中心层的概念没有明朗化,而且“任一微段……距离相等”严格来说应是一个极限的关系)。
通俗一点讲就是在曲面展开为平面的过程中其面上的任一个“纤维”长度保持不变。
很容易证明一下几个定理:定理一:如果某曲面可展开,则此展开是唯一的。
(唯一的意思是:如有两个平面图形都是某曲面的一个展开,则该两个平面图形必全等)定理二:如果某曲面是可展开的,那么它的任一部分也是可展开的。
现在我要告诉大家一个不好的消息,其实在诸多曲面中只有及其少量的曲面是可展开的,大量的曲面是不可展开的。
展开的分类:1、直接可展开的曲面(如由单一开口不自交轮廓拉伸形成的曲面等)。
2、剪开后可展开的曲面(如圆柱面、圆锥面等)。
我们经常遇到譬如有三个平钣(不在一个平面上)组成的零件,每两个平面有一条公共边(就像方盒子的一个角一样),此零件就不能直接展开但如果剪开其中的一条公共边,就可以展开了。
因此在SW的钣金中就有切口的概念。
3、可分为有限个部分展开的曲面(如圆柱面与圆锥面相结合的曲面等)。
4、不能展开的曲面(很容易证明如球面、椭球面等不可展开)钣金件的概念:以前SW的钣金在一个概念上是分得十分清楚的,如用一般的版金功能生成的钣金件都是可展开的,这相当于实际生产中的折角,滚圆等工艺。
可展曲面的表面展开图
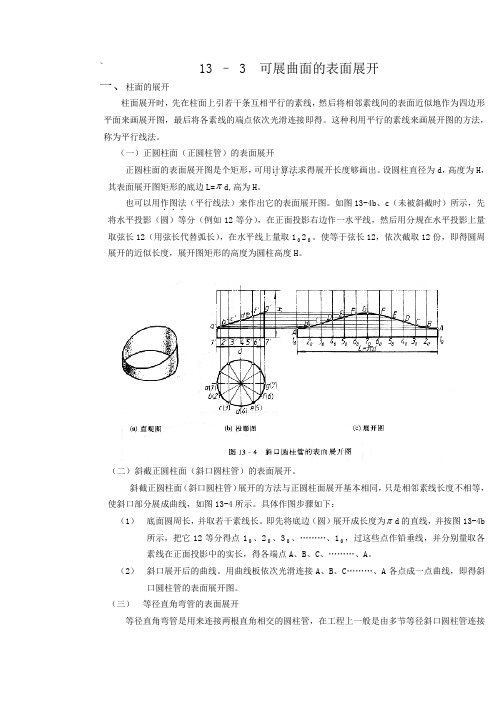
` 13 – 3 可展曲面的表面展开一、柱面的展开柱面展开时,先在柱面上引若干条互相平行的素线,然后将相邻素线间的表面近似地作为四边形平面来画展开图,最后将各素线的端点依次光滑连接即得。
这种利用平行的素线来画展开图的方法,称为平行线法。
(一)正圆柱面(正圆柱管)的表面展开正圆柱面的表面展开图是个矩形,可用计算法...求得展开长度够画出。
设圆柱直径为d,高度为H,其表面展开图矩形的底边L=πd,高为H。
也可以用作图法...(平行线法)来作出它的表面展开图。
如图13-4b、c(未被斜截时)所示,先将水平投影(圆)等分(例如12等分),在正面投影右边作一水平线,然后用分规在水平投影上量取弦长12(用弦长代替弧长),在水平线上量取102。
使等于弦长12,依次截取12份,即得圆周展开的近似长度,展开图矩形的高度为圆柱高度H。
(二)斜截正圆柱面(斜口圆柱管)的表面展开。
斜截正圆柱面(斜口圆柱管)展开的方法与正圆柱面展开基本相同,只是相邻素线长度不相等,使斜口部分展成曲线,如图13-4所示。
具体作图步骤如下:(1)底面圆周长,并取若干素线长。
即先将底边(圆)展开成长度为πd的直线,并按图13-4b所示,把它12等分得点10、2、3、………、1,过这些点作铅垂线,并分别量取各素线在正面投影中的实长,得各端点A、B、C、………、A。
(2)斜口展开后的曲线。
用曲线板依次光滑连接A、B、C………、A各点成一点曲线,即得斜口圆柱管的表面展开图。
(三)等径直角弯管的表面展开等径直角弯管是用来连接两根直角相交的圆柱管,在工程上一般是由多节等径斜口圆柱管连接而成,俗称虾米腰。
图13-1集粉管上边部分的弯管即为图13-5a 所示的等径直角弯管(近似于四分之一的圆环面),它的进出口是直径相等的圆柱孔,方向互相垂直。
此弯管实际上是由四段(两个半节,两个全节)组成的,其作图与单一斜口圆柱管基本相同。
画等径直角弯管展开图的步骤如下:(1)等径直角弯管的正面投影图,并按半节中心弧长等分1/4圆周,如图13-5b 。
第十三章 表面展开图

2 .斜棱柱表面的展开 1)斜棱柱
2)投影分析:
关键是求出正截面的实形,因为棱是垂直正截面
3)作图步骤:
① 作正垂面 P 、垂直于棱线,交棱线 于 1 '、 2' 、 3 '点,并求得其水平投影 △ 123 。 ② 用绕垂直轴旋转法求得正截面的实 形 △ 11 21 31 ,并将各边实长展开成为 一直线 l 。---- l 。 ③ 过 l 。、 2 。、 3 。、 l 。各点引 垂直线,并在对应直线上截取各棱线的 实长,得c。、 a 。、 b。、c。和 f0 、 d 。、 e 。、 f0 点; ④ 依次连接各点
2、近似锥面法
略
二、圆环面的近似展开 1、投影分析
2、作图步骤 ① 把 1 / 4 柱面分割成相等的 12 份,其间隔的近似值为 k ,并过各等分 点在正面投影图上画出圆柱的素线; ② 将圆柱底圆展开成为一直线,使其长度 l=k X12 . ③ 自各等分点画垂线,使它们分别等于相应素线的实长; ④ 光滑连接各端点
13.4 不可展曲面的表面展开
实质是:把不可展的曲面分解为若干较小的部分,然后将每 一小部分表面分解成为可展的平面、柱面或锥面进行展开 一、圆球面的近似展开 投影特点 : 1 .近似柱面法
① 沿经线方向等分圆球面 的水平投影为 12 份 ② 用相应部分的外切圆柱 面代替该部分圆球面 ③ 将正圆柱面的正面投影 也分割为 12 等份 ④ 以 k 为间隔距离,取相 应的长度 ⑤ 光滑连接所求各点,完 成该部分圆柱面的展开图
13.3 可展曲面的展开
一、柱面的展开 1 .截头正圆柱表面的展开
1)截头正圆柱 2)投影分析 3)作图步骤:
① 首先将圆柱底圆分割成 n ( n =12 )等份,并过各等份点在 正面投影图上画出圆柱的素线。 ② 将圆柱底圆展开成为一直线。 0。-12 。,并截取 12 等份, 点间的弧长近似值 k ; ③ 自各等分点作垂线,使它们 分别等于相应素线的实长
工程制图课件——展开图

πd
作图步骤:⑴ 将俯视图圆分成十二等分,并过各等分点在主视图上作出素线;
⑵ 将圆柱底圆的展开长度πd分成十二等分,过等分点作素线并在
其上求得各断点;
⑶ 光滑连接各点即得展开图。
12
作出五节直角弯管的展开图。 作图分析:多节圆柱弯管常用于通风、除尘的管道中。图示为一五节等径直 角弯管。其中中间的三节为整节(两面带斜口),端部的两节为半节(一面 带斜口)。 图中所示的半节斜面的倾斜角=11.25°。若将各节一顺一倒排列恰可构成
一圆管。因此如有现成的直圆管即可按图示位置切成五节,
第12章 展开图 •12.1 概 述 •12.2 平面立体的展开 •12.3 可展曲面的展开 •12.4 不可展曲面的近似展开
12.1.1展开图
12.1 概 述图
在工业生产中,经常遇到金属板材制件, 如防护罩、管道、容器、反应塔等。如图 12 - 1所示,为饲料粉碎机上的集粉筒, 它是由变形接头、圆锥管、偏交圆柱管和 四节弯管所组成,它们都是用板材卷曲焊 接而成。在制造这些板材制件时,必需先 在板材上画出制件的展开图(俗称放样), 然后按其下料成型,再将接缝焊接而成。 将制件表面按其实际形状大小,依次摊平 在同一平面上,称为表面展开。展开后所 得到的平面图形,称为展开图。
8
[例一] 图示为一变形接头,试画出该接头的展开图。
作图步骤:
⑴ 用直角三角形法求出图中
一般位置直线的实长;
⑵ 从视图左边的对称中心处
开始按三角形法依次展开各
表面;
⑶ 根据展开图下料后再按交线位置成型。
展开图的画法(非常有用)

1155
§8-2 可展曲面的展开
例8-6 已知圆柱面叉管的投影图,主管直径
为D1,支管直径为d1,试作其展开图。
最后,作主管 展开图。为了 便于作图,将 主管正截面 (底圆)展开 成长度为D1的 直线,使其位 于主管底圆正 面投影的延长 线上。
第一篇 画法几何 第八章 立体表面展开
1166
§8-2 可展曲面的展开
锥面
锥面可以看作为棱线无限增多的棱锥面, 因而其展开方法与棱锥面类似,采用三角 形法。
第一篇 画法几何 第八章 立体表面展开
1177
§8-2 可展曲面的展开
例8-7 已知截头圆锥的投影
图,试作其展开图。
圆锥面上各素线长度相等,在正 面投影中外形素线反映实长。锥底圆 的水平投影反映实形。 若圆锥没有 被截断,则它的展开图为一扇形,扇 形的半径L等于素线实长,扇形的弧长 等于直径为D的底圆的周长。 对于截 头圆锥,可通过截交线上点的正面投 影作水平线,与外形素线交于各点, 从而得到被截断的各素线实长。
第一篇 画法几何 第八章 立体表面展开
66
§8-1 多面体表面展开
例8-1 已知料斗下部出料管的投影图,试作其展
开图。
从展开作图可以看出, 这样展开所得到的上、下两 部分棱柱表面的展开图可以 拼画在一起,从而可节省板 料,而且上、下两部分连接 处的展开折线在安装时能准 确地拼合。
第一篇 画法几何 第八章 立体表面展开
变形接头
在圆形和矩形之间由平面和锥面组合而成的表 面为变形接头或方圆接头的表面,在钣金工中俗 称天圆地方。变形接头在工程中应用较广,如料 斗、管道中的渐变段等。
第一篇 画法几何 第八章 立体表面展开
2255
复习思考题
曲面展开

分别为U, 向网格线数量 向网格线数量。 N u , Nv -分别为 ,V向网格线数量。
近似展开中最佳展开基点的研究
2)最佳基点位置的假设 最佳展开基点位置主要与曲 面曲率的分布, 面曲率的分布,即曲面的弯曲状 况有关, 况有关,它的位置应有助于避免 在任一方向上产生较大的误差积 累。 于是提出如下的假设: 于是提出如下的假设:过最 佳展开基点的一对参数曲线把曲 面片分为四个区域, 面片分为四个区域,这四个区域 曲面展开的难易程度( 曲面展开的难易程度(产生误差 的可能性)应近似相同。 的可能性)应近似相同。
CATIA
二、曲面展开方法
2)专用系统 主要见 长与规则 曲面零件 的展开
二、曲面展开方法
2.基于物理模型的展开 2.基于物理模型的展开 (1)有限元逆向法
有限元逆向法( 有限元逆向法(一步 模拟法) 模拟法)的基本思想是在考 虑板料成形参数的前提下, 虑板料成形参数的前提下, 把工件模型离散化, 把工件模型离散化,忽略变 形的中间状态, 形的中间状态,经过逆向计 算,得到毛坯最初的轮廓形 状。有限元逆向法考虑了材 料加工时的实际变形情况, 料加工时的实际变形情况, 有利于成形、分析一体化。 有利于成形、分析一体化。
曲面展开 一、概述 二、曲面展开方法 三、所做的主要研究工作 近似展开中最佳展开基点的研究 四、有关文献与展望
一、概述
1.曲面展开的定义 1.曲面展开的定义 曲面Σ 曲面Σ1
∑ = f ( ∑1 )
平面Σ 平面Σ
曲面展开是曲面向平面的映射过程。 曲面展开是曲面向平面的映射过程。根据初始条件和映 射规则的不同,形成了不同的展开方法。 射规则的不同,形成了不同的展开方法。 2.可展曲面 2.可展曲面 (1)可展曲面是可以经过连续的延展变形,不发生皱褶和撕 可展曲面是可以经过连续的延展变形, 裂地与平面相贴合的曲面。 裂地与平面相贴合的曲面。 可展曲面可以准确地展开 为平面。 为平面。
CAD中曲面展开的技巧知识点

CAD中曲面展开的技巧知识点在计算机辅助设计(CAD)中,曲面展开是一项重要的技术,它允许我们将复杂的曲面体展开为平面形状,方便后续的加工和制作。
本文将介绍CAD中曲面展开的技巧知识点,帮助读者更好地理解和应用这一技术。
一、曲面展开的基本原理曲面展开是通过将曲面体沿着一定方向进行切割,并将各个切割表面展开到平面上来实现的。
在进行曲面展开前,我们需要先确定展开的方向和方式,这通常取决于曲面的形状和设计需求。
二、利用CAD软件进行曲面展开现代CAD软件提供了强大的曲面展开功能,可以自动计算和生成展开的平面图形。
下面是一些常用的CAD软件中曲面展开的技巧知识点:1. AutoCAD:在AutoCAD中展开曲面可以使用命令“FLATTEN”,通过选择需要展开的曲面体即可生成展开的平面图形。
2. SolidWorks:SolidWorks提供了多种展开曲面的工具,比如“铆接展开”和“整圆展开”等,通过选择合适的工具可以实现不同形状曲面的展开。
3. CATIA:在CATIA中,曲面展开主要使用“平面投影”和“拓扑转换”等功能,可以根据曲面的几何特征进行展开。
三、曲面展开的应用领域曲面展开技术广泛应用于各个领域,包括航空航天、汽车制造、建筑设计等。
下面介绍一些常见的应用场景:1. 飞机制造:在飞机制造中,翼型曲面的展开是关键步骤之一。
通过展开翼型曲面,可以得到翼面板的平面图形,方便后续的铆接和制造。
2. 汽车车身设计:汽车车身的曲面展开可用于生产车身板件的裁剪。
通过将曲面展开成平面,可以得到车身零部件的模具设计图纸。
3. 管道布局:在管道布局中,曲面展开可以帮助确定管道的几何形状和长度,确保管道的制造和安装的准确性。
四、曲面展开的技巧和注意事项在进行曲面展开时,有一些技巧和注意事项可以帮助提高展开结果的质量和准确性:1. 合理选择展开方向:根据曲面的形状和设计需求,合理选择展开的方向和方式,以确保展开后的平面图形能够满足后续的加工和制作要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O′
θ
O。
O
展开图
两面投影
画圆锥的展开图时,可先计算出圆锥展开后的扇形角,然后 根据扇形角和圆锥素线的长度,画出圆锥的展开图。 在展开图中, 扇形的圆心为圆锥
的中心,扇形半径等于圆锥的素线长度
L,扇形的弧长等于圆锥底圆的圆周D.
设扇形角为θ,则有:
O。
θ D 则
360° 2 L D L 180°
1′ 2′ 3′
4′
5′ 6′ 7′
1。
2。
3。
4。
5。
6。
7。
展开图
a(1) g(7)
b(2)
c(3) d(4)
f(6) e(5)
过各等分点1。、2。、 3。、……作铅垂线,在各铅垂线上量 取其素线的实长,分别得端点A、B、 C、……等。
两面投影
(4)曲线连接
e′ d′ a′ b′ c′ A B f′ g′ E F G
D
C B
E
A
(a)圆环管 等径直角弯管
(b)圆柱 管
D
C
1′ 2′ 3′
4′
5′ 6′ 7′
1。 2。
3。
4。
5。
6。
7。
展开图
a(1)
g(7)
b(2) c(3) d(4)
f(6) e(5)
用光滑的曲线依次连接A、B、 C、……等各点,即得斜口圆柱管的 展开图。
两面投影
4. 等径直角弯管的展开
在管道设计中,等径直角弯管用来连接两根垂直相交、且直径相 等的圆管。由于圆环是不可展曲面,因此在设计弯管时,一般不采用 图(a)所示的圆环,而是采用多段圆柱组成,如图(b)所示。图(b) 示为工程上常用的五节斜口圆管拼接而成的直角弯管,中间三节叫全 节,首尾两节叫半节,半节可用一个全节在对称面处分开得到。
可展曲面的展开
1. 圆柱表面的展开
H
H
L=
πD
展开图
圆柱表面的展 开图为一矩形, 矩形的一组对边 为圆柱上、下低 圆的周长,另一 组对边为圆柱素 线的实长。
两面投影
作图方法
按俯视图中的水平圆 周展开成一直线,并在两 端点作垂线与圆柱等高, 封闭图形即得展开图。
展开图
两面投影
2. 圆锥表面的展开
圆锥的表面展开为一扇形,如图所示为圆锥的两面投影图及其 展开图。
展开图
θ
圆锥台的表面展开图是两个同圆心的扇形面积相差的部分,如 图所示,为圆锥台的两面投影及其展开图。
展开图 两面投影
3 斜口圆柱管的展开
e′
d′ a′ b′ c′ A B f′ g′ E D C F G
方法与步骤:
(1)等分圆周
(2)圆周展开
1′ 2′ 3′
4′
5′ 6′ 7′
1。 2。
3。
4。
f(6) e(5)
两面投影
(2)圆周展开
e′ d′ a′ b′ c′
f′
g′
在展开图中按周长展开圆周 成直线,并将其十二等分。
1′ 2′ 3′
4′
5′ 6′ 7′
1。
2。
3。
4。
5。
6。
7。
展开图
a(1)
g(7)
b(2) c(3) d(4)
f(6) e(5)
两面投影
(3)量取实长
e′ d′ a′ b′ c′ A B f′ g′ E D C F G
5。
6。
7。
(3)量取实长
(4)曲线连接
展开图
a(1) g(7)
b(2) c(3) d(4)
f(6) e(5)
两面投影
(1)等分圆周
e′ d′ a′ b′ c′
f′
g′
将俯视图的圆周十二等分,并在主视图 上画出各分点的素线长度,
1′ 2′ 3′
4′
5′ 6′ 7′
a(1)
g(7)
b(2) c(3) d(4)
