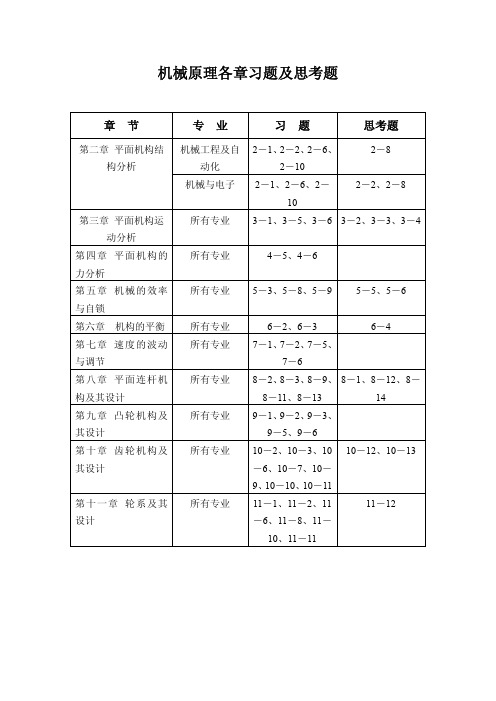
机械的效率和自锁(有答案)
西工大教材-机械原理各章习题及答案
电动机所需的功率为
p = ρ • v /η = 5500 ×1.2 ×10−3 / 0.822 = 8.029(KW )
5-8 在图示斜面机构中,设已知摩擦面间的摩擦系数 f=0.2。求在 G 力作用下(反行程),此斜面 机构的临界自锁条件和在此条件下正行程(在 F 力作用下)的效率。 解 1)反行程的自锁条件 在外行程(图 a),根据滑块的平衡条件:
解 1 ) 取 比 例 尺 μ 1 = 1mm/mm 绘 制 机 构 运 动 简 图 ( 图 b )
(a)
2 )计算该机构的自由度
n=7
pι=9
ph=2(算齿轮副,因为凸轮与齿轮为一体) p’=
F’= F=3n-2pe-ph
=3x7-2x8-2 =1
G7
D 64 C
EF
3
9
B
2
8
A
ω1
b)
2-6 试计算如图所示各机构的自由度。图 a、d 为齿轮一连杆组合机构;图 b 为凸轮一连杆组合 机构(图中在 D 处为铰连在一起的两个滑块);图 c 为一精压机机构。并问在图 d 所示机构中, 齿轮 3 与 5 和齿条 7 与齿轮 5 的啮合高副所提供的约束数目是否相同?为什么?
C3 重合点继续求解。
解 1)速度分析(图 b)取重合点 B2 与 B3,有
方向 大小 ?
v vv vB3 = vB2 + vB3B2 ⊥ BD ⊥ AB // CD ω1lAB ?
D
C
3 d3
ω3
4
ω3 90°
2
B(B1、B2、B3)
ω1
A1 ϕ = 90°
第5章机械的效率和自锁

P1 1
P’1
P2
Pk
2
k
P’2
P’k
Pr
总效率η不仅与各机器的效率ηi有关,而且与传递的功率 Pi有关。
设各机器中效率最高最低者分别为ηmax和ηmin 则有:
ηmin<η <ηmax
3.)混联 先分别计算,合成后按串联或并联计算。
P1 1
P2 P’d23‘ P’d3 4‘P’r 2
Pd
P”d23“ P”d3 P4“kP”r
无论F多大,滑块在F的作用下不可能运动
FR Ft F Fn
φβ 1
Ff
2
当驱动力的作用线落在摩擦角(锥)内时,则机械发生 自锁。
5.4.2转动副的自锁
a
对仅受单力F作用的回转运动副产 生的力矩为: Md=F·a
最大摩擦力矩为: Mf =FRρ
1F FR
2
当力F的作用线穿过摩擦圆(a<ρ)时,发生自锁。
Ff 21
简单平面移动副
2 FN21 G
Ff 21 fFN21 fG
v FN21
12
F 1
G
●槽面接触: fv= f / sinθ
G=(FN21 /2)sinθ+(FN21 /2)sinθ FN21 = G / sinθ Ff21= f FN21
= G (f / sinθ) =G fv
fv─当量摩擦系数。
第5章 机械的效率和自锁
本章教学内容
5.1运动副中摩擦力的确定 5.2考虑摩擦时机构的受力分析 5.3机构的效率 5.4机构的自锁
5.1 运动副中的摩擦力的确定
5.1.1移动副中摩擦力的确定
●水平面接触:
Ff 21 fFN21
孙桓《机械原理》【教材精讲+考研真题解析】(第五章机械的效率与自锁)【圣才出品】

第5章机械的效率与自锁[视频讲解]5.1本章要点详解本章要点■机械效率的定义及其计算方法■提高机械效率的措施■机械的自锁现象及其应用■机械的自锁条件及其确定重难点导学一、机械的效率1.机械效率的概念及意义(1)概念①机械效率机械的输出功与输入功之比称为机械效率,它反映了输入功在机械中的有效利用程度,以 表示。
②损失率机械的损失功(W f)与输入功(W d)的比值称为机械损失系数或损失率,以ξ表示。
(2)意义①机械效率反映了输入功在机械中的有效利用的程度。
②机械效率是机械中的一个主要性能指标。
③因摩擦损失是不可避免的,故必有ξ>0和η<1。
2.机械效率的确定(1)机械效率的计算确定①以功表示的计算公式式中W r表示有效功、W f表示损失功、W d表示总功。
②以功率表示的计算公式式中P r表示有效功率、P f表示损失功率、P d表示总功率。
③以力或力矩表示的计算公式η=F0/F=M0/M式中M0和M分别表示为了克服同样生产阻力所需的理想驱动力矩和实际驱动力矩,所以其计算公式也可表示为(2)机械效率的实验测定机械效率的确定除了用计算法外,更常用实验法来测定,许多机械尤其是动力机械在制成后,往往都需作效率实验。
3.机组的机械效率计算已知机构的效率可计算确定整个机构的效率。
常用机构的效率见如表5-1-1所示。
表5-1-1简单传动机构和运动副的效率(1)机组的定义由若干个机器组成的机械系统称为机组。
当已知机组各台机器的机械效率时,则该机械的总效率可由计算求得。
(2)机组的分类①串联机组如图5-1-1所示,由k个机器串联组成的机组,设各机器的效率分别为1η、2η、…、η,则串联机组的效率为k图5-1-1串联机组由此可见,只要串联机组中任一机器的效率很低,就会使整个机组的效率极低;且串联机器的数目越多,机器的效率也越低。
因此,提高串联机组机械效率的方法有:a.减少串联机构的数目;η。
b.提高机组中最小的机械效率min②并联机组如图5-1-2所示,由k个机构并联组成的机组,设各机构的效率分别为1η、2η、……kη,则并联机组的效率为图5-1-2并联机组由此可见,并联机组的特点有:a.机组的输入功率为各机器的输入功率之和,而其输出功率为各机器的输出功率之和。
机械原理机械的效率和自锁

P2 3 P3 4 P4 5 Pr
混联组合机器的总效率
Pr
Pd
η′—串联机构的效率
η″—并联机构的效率
例1 在图示的电动卷扬机中,已知其每一对齿轮的效率η12、 η2′3 以及鼓轮的效率η4均为0.95,滑轮的效率η5为0.96,载荷 Q = 50000N。其上升的速度V=12m/min , 求电机的功率?
(2)并联组合机器的效率计算
各机器的输入功率为: P1、P2 、…、PK ,
输出功率为: P1 P1 1 P2 P2 2 PK PK K
并联机组的特点:
※机组的输入功率为各机器输入功率之和;Pd —机器的输入功率
Pd P1 P2 P3 PK
Pd Pr /1 2 34 5 0.2 /(0.982 0.942 0.42) 0.561KW
机构的总效率为:
Pr Pd
Pr Pd
PPdr
5 0.2 0.837 5.649 0.561
§5-2 机械的自锁
2. 每一路的总效率分别为:
2
1
18 12 34 56 78
0.953 0.92 0.79
114 12 910 1112 1314
0.953 0.92 0.79
6
5
11 12
84
3 13
7
9 10
14
3.
整个机构的总效率为:
1 2 0.98, 3 4 0.96, 3 4 0.94, 5 0.42;
并已知输出的功率分别为 Pr 5KW, Pr 0.2KW.
求该机械传动装置的机械效率。
机械的效率和自锁

F = G tan(α − 2ϕ )
结束
§2 机械的自锁
四、举例
3、偏心卡具:在工件反力作用下的自锁条件 、偏心卡具:
结束
§2 机械的自锁
四、举例
3、偏心卡具:在工件反力作用下的自锁条件 、偏心卡具: 去除后,卡具不松脱, F 去除后,卡具不松脱,则必 须使反力FR23与摩擦圆 ρ 相割 由几何条件: 由几何条件: S-S ≤ ρ 由直角三角形ABC知: 知 由直角三角形 S1 = AC = R sinϕ ϕ 又由直角三角形OAE知: 知 又由直角三角形 S = OE = e sin(δ - ϕ ) 自锁条件: 自锁条件: O δ s1
自锁条件: 自锁条件: a [ ρ 驱动力(外力的合力)作用于摩擦圆之内时,则发生自锁。 驱动力(外力的合力)作用于摩擦圆之内时,则发生自锁。
结束
§2 机械的自锁
三、自锁时的力学特征
3、机械的自锁 、
1)由力分析求得的机械可以克服的生产阻力 G ≤ 0 ) 2)机械效率 η ≤ 0(效率越小自锁越可靠) ) (效率越小自锁越可靠)
§1 机械的效率
一、机械效率及其表达形式
1、机械效率 η Wd = Wr + Wf
输入功 (动力)
输出功 (克服生产阻力)
损耗功 (摩擦等)
机械效率: 机械效率:
η = Wr / Wd = 1 - Wf / Wd
机械损失率: 机械损失率: ξ = Wf / Wd
η + ξ = 1 损失不可避免 Wf → ξ > 0; η < 1 ;
s
.E
C R23 A ϕ B
e
F
D
ρ
e sin(δ − φ ) − R sin ϕ ≤ ρ
机械原理各章问答答案

机械原理各章问答答案机械原理问答题1.什么是机构、机器和机械?答:机构:在运动链中,其中一个件为固定件(机架),一个或几个构件为原动件,其余构件具有确定的相对运动的运动链称为机构。
机器:能代替或减轻人类的体力劳动或转化机械能的机构。
机械:机器和机构的总称。
2.机器有什么特征?答:⑴经过人们精心设计的实物组合体。
⑵各部分之间具有确定的相对运动。
⑶能代替或减轻人的体力劳动,转换机械能。
3.机构有什么特征?答:⑴经过人们精心设计的实物组合体。
⑵各部分之间具有确定的相对运动。
4.什么是构件和零件?答:构件:是运动的单元,它可以是一个零件也可以是几个零件的刚性组合。
零件:是制造的单元,加工制造不可再分的个体。
1.什么是平面机构?答:组成机构的所有构件都在同一平面或相互平行的平面上运动。
2.什么是运动副?平面运动副分几类,各类都有哪些运动副?其约束等于几个?答:运动副:两个构件直接接触而又能产生一定相对运动的联接叫运动副。
平面运动副分两类:(1)平面低副(面接触)包括:转动副、移动副,其约束为 2。
(2)平面高副(点、线接触)包括:滚子、凸轮、齿轮副等,约束为 1。
3.什么是运动链,分几种?答:若干个构件用运动副联接组成的系统。
分开式链和闭式链。
4.什么是机架、原动件和从动件?答:机架:支承活动构件运动的固定构件。
原动件:运动规律给定的构件。
从动件:随原动件运动,并且具有确定运动的构件。
5.机构确定运动的条件是什么?什么是机构自由度?答:条件:原动件的数目等于机构的自由度数。
机构自由度:机构具有确定运动所需要的独立运动参数。
6 .平面机构自由度的计算式是怎样表达的?其中符号代表什么?答:F =3n- 2P L-P H其中:n----活动构件的数目,P L----低副的数目,p H----高副的数目。
7.在应用平面机构自由度计算公式时应注意些什么?答:应注意复合铰链、局部自由度、虚约束。
8.什么是复合铰链、局部自由度和虚约束,在计算机构自由度时应如何处理?答:复合铰链:多个构件在同一轴线上组成转动副,计算时,转动副数目为m-1个局部自由度:与整个机构运动无关的自由度,计算时将滚子与其组成转动副的构件假想的焊在一起,预先排除局都自由度。
机械原理(机械效率和自锁)

输入功—在一个机械系统中,驱动力(或驱动力矩)所作的功 称为输入功,用Wd 表示;
输出功—在一个机械系统中,克服工作阻力(或驱动力矩)所 作的功,称为输出功,用Wr 表示;
损失功—在一个机械系统中,克服有害阻力(如摩擦阻力、空) 气阻力等)所作的功,称为损失功,用Wf表示;
机械在稳定运转时期,输入功等于输出功与损耗功之和,即:
G0、M0 — 理想工作阻力、理想工作阻力矩;
G、M — 实际工作阻力、实际工作阻力矩;
当需计算整台机器或整个机组的机械效率时,常用以下三种 方法,其中在实际设计中,更常用到的是实验法和经验法, 即确定机械效率的三种方法分别为: 计算法 实验法 —对于已有的机器,可以用实验法直接测得机械效率。 经验法 —对于正在设计和制造的机器,不能直接用实验法测
定效率,但由于各种机器都是由一些基本机构组合而 成,而这些基本机构的效率通过实验积累的资料却是 可以预先估定的,在已知这些基本机构和运动副的机 械效率后,就可以通过计算确定出整个机器的效率。 同理,对于由多个机器组成的机组,只要知道各台机 器的效率,就可以根据各机组的组合情况用计算的办 法求出该机组的总效率。(见P76表5-1) 三种不同机器组合的效率计算
Pd
Pd
令式中: Pr
Pd
得到机械效率的表达式为:
1
Pf
令: Pf Wf
Pd
Pd Wd
效率恒小于1
— 机械损失系数 1
由于机械摩擦不可避免,故必有: 0, 1
由以上公式可知:为使其具有较高的机械效率,应尽量减小 机械中的损耗,主要是磨擦损耗。这就要求:一方面应尽量 简化机械传动系统,使功率传递通过的运动副数目越少越好。 另一方面,应设法减少运动副中的磨擦,如采用滚动磨擦代 替滑动磨擦,选用适当的润滑剂及润滑装置进行润滑,合理 选用运动副元素的材料等。
机械原理5机械效率与自锁

一、机械的效率
机械在稳定运转阶段恒有: Wd= Wr+Wf η =Wr / Wd =(Wd-Wf) /Wd =1-Wf /Wd
比值Wr / Wd反映了驱动功的有效利用程度, 称为机械效率。
用功率表示:η =Nr / Nd =(Nd-Nf) /Nd
=1-Nf /Nd
分析:η 总是小于 1,当Wf 增加时将导致η 下降。
以上为效率计算方法,工程上更多地是用实验法
测定η ,表5-1列出由实验所得简单传动机构和运
动副的机械效率(P69-P70)。
表5-1 简单传动机械和运动副的效率
名称
传动形式
效率值
备注
圆柱齿 轮传动
6~7级精度齿轮传动
8级精度齿轮传动 9级精度齿轮传动 切制齿、开式齿轮传动
铸造齿、开式齿轮传动
6~7级精度齿轮传动
拧紧时:
M
d2 2
Gtg(
v )
理想机械: M0=(d2 G tgα) / 2 η=M0 / M =tgα/tg(α+φv )
拧松时,驱动力为G,M’为阻力矩,则有:
实际驱动力:
G=2M’/d2 tg(α-φv )
理想驱动力: ∴
G0=2M’/d2 tgα η’=G0/G =tg(α-φv ) / tgα
良好跑合、稀油润滑 稀油润滑 干油润滑
0.40~0.45 0.70~0.75
0.75~0.82 0.80~0.92 0.85~0.95
润滑良好
名称 带传动
链传动 摩擦轮
传动 滑动轴承 滚动轴承
螺旋传动
续表5-1 简单传动机械和运动副的效率
传动形式
效率值
备注
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§5 机械的效率和自锁
填空题:
1.设机器中的实际驱动力为r
P ,在同样的工作阻力和不考虑摩擦时的理想驱动
力为r P 0,则机器效率的计算式是η = r P 0/r
P 。
2.设机器中的实际生产阻力为r
Q ,在同样的驱动力作用下不考虑摩擦时能克服
的理 想生产阻力为r Q 0,则机器效率的计算式是 η= r Q /r
Q 0 。
3.假设某机器由两个机构串联而成,其传动效率分别为1η和2η,则该机器的传动效率为 1η*2η 。
4.假设某机器由两个机构并联而成,其传动效率分别为1η和2η,则该机器的传动效率为 (P 1*η1+ P 2*η2)/(P 1+P 2) 。
5. 从受力观点分析,移动副的自锁条件是 外力的作用线与运动方向法线的夹角小于等于摩擦角 ;转动副的自锁条件是 外力的作用线与摩擦圆相切或相割 ;从效率观点来分析,机械自锁的条件是 效率小于等于零 。
综合题1:
某滑块受力如图所示,已知滑块与地面间摩擦系数f ,试求F 与Q 分别为驱动力时的机构运动效率。
F 为驱动力:f tg
1
-=ϕ
于是由正弦定理:)
90sin()
90sin(0
0ϕθϕ--+=Q F 令0=ϕ,得)
90sin(0
0θ-=Q
F 因此,其效率为)
90sin()90sin()
90sin(0
0θϕϕθη-+--==
F F 当Q 为驱动力,F 变为阻力,取ϕ-代替上式中的ϕ
θ-
)
90sin()
90sin(
90
sin(0
00ϕθϕθη+---==)F F 第四章习题中,综合题5,要求计算该机构效率。
(可直接利用前面的计算结果)
0153077.8==-f tg ϕ
由正弦定理:
)90sin()2180sin(0
210ϕβγϕ-=--+R P 和)
90sin()2sin(012ϕϕβ+=-R Q 于是
Q P *-+*---+=)
2sin()90sin()90sin()2180sin(00ϕβϕϕβγϕ
代入各值得:N P 7007.1430=
取上式中的0
0=ϕ,可得N P 10000=
于是6990.00
==
P
P η
综合题2:
图 示 为 由 A 、B 、C 、D 四 台 机 器 组 成 的 机 械 系统,设 各 单 机 效 率 分 别 为ηA 、ηB 、ηC 、
ηD , 机 器B 、D 的 输 出 功 率 分 别 为N B 和N D 。
(1) 试 问 该 机 械 系 统 是属 串 联、 并 联 还 是 混联 方 式 (2) 写 出 该 系 统 应 输 入 总 功 率N 的 计 算 式。
综合题3:
已知机构位置图、摩擦圆半径ρ、摩擦角ϕ如图所示。
图中r
Q 为已知生产阻力。
试
(1) 在 图 中 画 出 各 运 动 副 总 反 力 作 用 线 ( 方 向、 位 置 及 指 向 ); (2) 求 出 机 构 在 图 示 位 置 的 驱 动 力r
P 及 瞬 时 效 率η 。
μl =0002. m/mm
综合题4:
图 示 楔 块 装 置, 两 面 摩 擦 系 数 均 为f 。
求 将 楔 块1 打 入2 后 能 自 锁 的 条 件。
即 撤 去r
P 力 后, 在 楔 紧 力 作 用 下, 楔 块1 不 能 脱 出 的 条 件。
综合题5:
图 示 楔 块 夹 紧 机 构。
各 摩 擦 面 间 的 摩 擦 系 数 为f , 正 行
程 时r Q 为 阻 力,r
P 为 驱 动 力。
试 求:
(1) 该 机 械 装 置 正 行 程 的 机 械 效 率η ( 用α 和 摩 擦 角 表 示)。
(2) 反 行 程 欲 自 锁,α 角 应 满 足 什 么 条 件。
