用单位“1”解决实际问题.doc
《转化单位“1”解决实际问题》专项培优

《转化单位“1”解决实际问题》专项培优典型例题例水果店运来三种水果,其中苹果的筐数是梨与香蕉筐数和的12,香蕉的筐数是苹果与梨筐数和的13,梨有30筐,这三种水果共有多少筐分析把总筐数看做单位“1”,再把题中含有分数的句子进行转化,最后找30的对应分数。
根据“苹果的筐数是梨与香蕉筐数和的12”可知,梨与香蕉筐数的和为2份,苹果的筐数为1份,即苹果的筐数占三种水果筐数和的112+;同理,香蕉的筐数占三种水果筐数和的113+。
所以,梨的筐数占三种水果筐数和的(1-112+-113+)。
解答30÷(1-112+-113+)=72(筐)答:这三种水果共有72筐。
反馈练习1.小刚、小强、小兰、小婷一共栽了60棵树,小刚栽的棵数是其他三人栽树总棵数的一半,小强栽的棵数是其他三人栽树总棵数的13,小兰栽的棵数是其他三人栽树总棵数的14。
小婷栽了多少棵树2.猴王把一堆桃子分给大、中、小三只猴子。
大猴说:“我分到的桃子是它俩的和。
”中猴说“我分到的桃子是它俩和的一半。
”小猴说:“我分到18个桃子。
”这堆桃子共有多少个3.甲、乙、丙三辆汽车共运走一堆煤,甲车运走了总吨数的40%,乙车运的是丙车的35,已知甲车比乙车多运了28吨,这堆煤共有多少吨4.甲、乙两人各有钱若干,现有18元奖金,如果全部给甲,则甲的钱数是乙的2倍,如果全部给乙,则乙的钱数为甲的78,则原来两人各有多少钱5.光明机械厂两天生产一批零件,用同样的箱子包装,第一天加工这批零件的45%,装满4箱,还剩60个,第二天生产的连同第一天装剩下的,正好又装满6箱,这批零件有多少个参考答案:×(1-112+-113+-114+)=13(棵)提示:把四个人的栽树总棵数看做单位“1”,根据“小刚栽的棵数是其他三人栽树总棵数的一半”可知,小刚栽的棵数占四人栽树总棵数的112+;根据“小强栽的棵数是其他三人栽树总棵数的13”可知,小强栽的棵数占四人裁树总棵数的113+;根据“小兰栽的棵数是其他三人栽树总棵数的14”可知,小兰栽的棵数占四人栽树总棵数的114+。
解决问题(利用抽象的“1”解决实际问题)-人教版六年级数学上册教案

解决问题(利用抽象的“1”解决实际问题)在人教版六年级数学上册中,有一个有趣的教学内容:利用抽象的“1”来解决实际问题。
这种方法能够帮助学生提高抽象思维能力,帮助他们更好地理解数学概念和解决数学问题。
下面将介绍这种方法在教学中的应用。
第一步:理解抽象的“1”在日常生活中,我们经常使用数字“1”来表示数量、长度、重量等,它是一个具体的数值。
但在数学中,“1”不仅仅是一个简单的数字,在数学中具有着更为广泛的意义,它可以用来表示不同单位的同一量数,起到了标准化的作用,也可以作为代数中的常量,在表示式中起到重要的作用。
第二步:以抽象的“1”解决实际问题举例说明,当我们要测量一段铁轨的长度时,如果使用尺子,可能需要不断地调整、移动,很难做到精确测量。
但如果我们将这段铁轨分成若干“1”的长度,可以用标尺或直尺轻松地测量出长度。
这种方法可以让学生更好地理解测量数据、标准单位等概念。
另外,抽象的“1”还可以帮助解决更为复杂的数学问题。
比如,当我们计算1+2+3+…+100的和时,可以将问题转化为100个1的总和,再进行计算,这样既简单又便于理解。
此外,当我们进行约分操作时,也会用到抽象的“1”,将分数化为相同的分母,方便计算。
第三步:教师应用抽象的“1”进行教学在教学中,教师可以通过讲解并引导学生使用抽象的“1”来解决问题。
比如在进行有关测量、单位换算的教学时,教师可以引导学生将物品拆分成若干个“1”并进行标准单位换算,或者进行相应的加减操作。
同时,在解决数学问题时,让学生尝试使用抽象的“1”进行转化,优化计算过程。
结论在数学教学中,抽象的“1”是一个非常重要的概念,通过使用它,帮助学生加深对数学概念的理解,提高其数学抽象思维能力。
因此,教师应该积极地将其应用到教学中,让学生通过多样化的学习方式来获得更好的学习效果。
6.5 用单位“1”解决实际问题(导学案)- 2023-2024学年数学 六年级上册 人教版

6.5 用单位“1”解决实际问题(导学案)2023-2024学年数学六年级上册人教版教学内容本节主要介绍如何运用单位“1”解决实际问题。
单位“1”在数学中是一种重要的概念,通过将问题转化为单位“1”的比例关系,可以简化问题的解决过程。
教学内容包括理解单位“1”的定义,掌握将实际问题转化为单位“1”的比例关系的方法,以及运用单位“1”解决实际问题。
教学目标1. 理解单位“1”的概念和意义;2. 学会运用单位“1”解决实际问题;3. 培养学生的逻辑思维能力和问题解决能力。
教学难点1. 理解单位“1”的概念;2. 将实际问题转化为单位“1”的比例关系;3. 运用单位“1”解决实际问题。
教具学具准备1. 教师准备:PPT课件、教学视频、示例题目;2. 学生准备:笔记本、笔、计算器。
教学过程1. 引入:通过一个实际问题引入单位“1”的概念,让学生思考如何用单位“1”来表示这个问题;2. 讲解:讲解单位“1”的定义和意义,通过示例题目展示如何将实际问题转化为单位“1”的比例关系;3. 练习:让学生分组讨论,运用单位“1”解决实际问题,教师进行指导和解答;4. 总结:总结本节课的重点内容,强调单位“1”在解决实际问题中的作用。
板书设计1. 板书6.5 用单位“1”解决实际问题;2. 板书内容:单位“1”的定义、将实际问题转化为单位“1”的比例关系、示例题目。
作业设计1. 基础题:完成教材上的练习题目;2. 提高题:运用单位“1”解决实际问题,并写出解题过程;3. 拓展题:研究单位“1”在其他数学问题中的应用。
课后反思本节课通过引入实际问题,让学生理解和掌握了单位“1”的概念和运用方法。
在教学过程中,学生积极参与讨论和练习,提高了他们的逻辑思维能力和问题解决能力。
但也存在一些问题,如部分学生对单位“1”的理解还不够深入,需要在今后的教学中加强练习和讲解。
教学难点本节课的重点是理解单位“1”的概念和如何将实际问题转化为单位“1”的比例关系。
第6课时 用单位“1”解决实际问题

第6课时 用单位“1”解决实际问题(教材例5,P90~91)一、我会填。
1.甲数比乙数少10%,乙数比丙数多10%,甲数是丙数的( 99 )%。
2.小明数学测验连续两次增长5%,两次成绩共增加( 10.25 )%。
3.一批树木的成活率为95%,经过技术改良后,未成活的树木减少了10%,现在这批树木的成活率达到( 95.5 )%。
二、我会判断。
1.去年比前年增产15%,今年又比去年增产15%,两年一共增产30%。
( × )2.王阿姨卖了两件衣服,都是60元,一件赚20%,另一件亏20%,正好没赚也没亏。
( × )3.一楼盘每平方米房价先提价10%,再降价10%,现在每平方米房价和原价相同。
( × )三、我会选。
1.(30-20)÷20=50%,表示( A )。
A .30比20多50%B .20比30少50%C .30是20的50%2.如果a :35=b ×62.5%=c ÷62.5%(a 、b 、c 均不为0),那么( B )。
A .a 最大 B .b 最大 C .c 最大3.长方形的长和宽各增加10%,那么新长方形面积比原长方形面积增加( C )%。
A .105B .20C .21四、解决问题。
1.蔬菜市场运回一批蔬菜,茄子的质量比西红柿多15%,辣椒的质量比茄子少20%。
辣椒的质量是西红柿的百分之几?(1+15%)×(1-20%)=92%答:辣椒的质量是西红柿的92%。
2.某品牌冰箱进行促销活动,降价10%,在此基础上,商场又按售价的5%赠送礼品,此时买这个品牌的冰箱,相当于降价百分之几?1-(1-10%)×(1-5%)=14.5%答:相当于降价14.5%。
五、据调查,某地十月份的猪肉价格比九月份下降了10%,十-月份又比十月份上涨12%。
十-月份猪肉价格比九月份是涨了还是跌了?涨跌幅度是多少?(仿教材P93第11题)1×(1-10%)×(1+12%)=1.008涨:(1.008-1)÷1×100%=0.8%答:涨了,涨幅是0.8%。
三年级下册数学教案8.1:应用几分之一解决实际问题

三年级下册数学教案-8.1:应用几分之一解决实际问题数学是我们身边最常见的学科,任何一个行业都离不开它。
数学的基础知识非常重要,每一项知识都是不可或缺的。
几分之一是数学中一个重要的概念,它在实际问题中的应用也非常广泛。
今天我们来学习一下应用几分之一解决实际问题。
一、教学目标1、学生能够理解几分之一的含义,并运用几分之一解决简单的实际问题。
2、学生能够根据实际情况,灵活运用几分之一,进行计算和分析。
3、学生能够善于思考,举一反三,更好地应用几分之一解决实际问题。
二、教学重难点重点:让学生正确理解几分之一的含义,善于运用几分之一解决实际问题。
难点:让学生能够将几分之一运用到实际问题中,进行分析和解决。
三、教学内容1、几分之一的含义几分之一是将一个整体,按照等分的方式,分成等份,其中每份被称为几分之一。
例如,将一个蛋糕分成4份,每份就是蛋糕的四分之一。
2、应用几分之一解决实际问题(1)例题:小明有8个橙子,他想分给小红四分之一,小白三分之一。
他每次分两个橙子。
问他需要分几次才能分完?解析:小明有8个橙子,根据题意可知,他要将橙子分成四份和三份。
需要将8个橙子分成12份(4+3=7,4/7,3/7)。
每一次分两个橙子,相当于将橙子分成6份。
他需要分6次才能分玩。
(2)例题:一个篮球场,分为四份,A、B、C、D四个区域。
其中A区域有几分之一的人,B区域有三分之一的人,C区域有八个人,问D区域有多少人?解析:将篮球场分为四份,根据题意可知,A、B、C区域的人数。
需要先计算出一个份为总人数的四分之一。
假设篮球场中有40个人,则A区域有40/4=10个人。
B区域有40×3/12=10个人。
C区域有8个人。
D区域有40-10-10-8=12个人。
四、教学方法1、讲授法:教师以简单易懂、生动有趣的方式,结合实际例子,向学生讲解几分之一的概念和应用。
2、问答互动法:教师提出问题,在课堂上与学生进行问答互动,激发学生的思考和兴趣。
求单位“1”的练习题
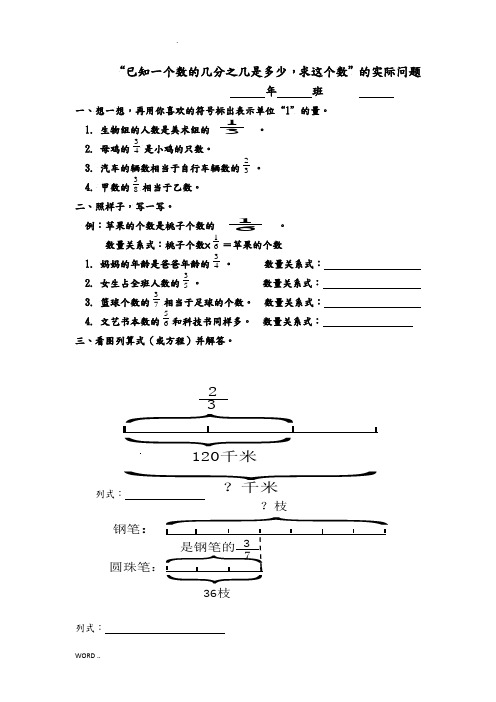
“已知一个数的几分之几是多少,求这个数”的实际问题年 班 一、想一想,再用你喜欢的符号标出表示单位“1”的量。
1. 生物组的人数是美术组的31。
2. 母鸡的43是小鸡的只数。
3. 汽车的辆数相当于自行车辆数的32。
4. 甲数的83相当于乙数。
二、照样子,写一写。
例:苹果的个数是桃子个数的61。
数量关系式:桃子个数×61=苹果的个数 1. 妈妈的年龄是爸爸年龄的43。
数量关系式:2. 女生占全班人数的53。
数量关系式:3. 篮球个数的73相当于足球的个数。
数量关系式:4. 文艺书本数的65和科技书同样多。
数量关系式:三、看图列算式(或方程)并解答。
列式:列式:120千米23?千米36枝钢笔:是钢笔的73?枝四、列式计算。
1. 一个数的43是2112,这个数是多少?2. 一个数的54是20,这个数的258是多少?五、找朋友(问题、算式一线牵)。
妈妈今年40岁,妈妈的年龄是爸爸年龄的98,明明的年龄是妈妈年龄的51。
40×51爸爸今年多少岁?40÷98妈妈和明明一共多少岁?40+40×51妈妈和爸爸一共多少岁?40+40÷98明明今年多少岁?六、走进生活,解决问题。
1. 小岩买了一瓶橙汁,喝了53,正好是300毫升,这瓶橙汁总量是多少毫升?2. 实验小学参加艺术班的学生有1080人,占全校学生总数的52,全校共有学生多少人?3. 同学们做了16朵红花,做的黄花的朵数是红花的45,又是蓝花的1110。
做的蓝花有多少朵?七、智力大比拼!你能根据所给的算式编出数学应用题吗?赶快试一试吧!90÷43120×525、稍复杂的“已知一个数的几分之几是多少,求这个数”的实际问题年班一、看图填空。
1. 苹果树棵数是桃树棵数的,比桃树多。
2. 桃树棵数是苹果树棵数的,比苹果树少。
二、想一想,填一填。
1. 50是80的,80比50多。
( )( ) ( )( ) ( )( ) ( )( )苹果树棵数:桃树棵数: ( )( ) ( )( )你能行!2. 篮球的数量比足球多41,篮球的数量是足球的 。
重难点强化小专题(五) 用抽象的“1”解决

重难点强化小专题(五) 用抽象的“1”解决实际问题一、我会选。
1.一件工作,甲独做10小时完成,乙独做12小时完成,丙独做15小时完成。
三人合做( B )小时可以完成这件工作。
A .3B .4C .52.编写一份稿件,甲单独写4天写完,乙单独写5天写完。
如果两人共同编写这份稿件的45,需要几天?正确的列式是( C )。
A .(4+5)÷45 B.45÷(4+5) C.45÷(14+15) 二、解决问题。
1.双“11”快递装满一车厢,小李单独送要6天送完,小王单独送要5天送完。
两人合送,几天后还剩下这车厢货物的13? (1-13)÷(16+15)=2011(天) 答:2011天后还剩下这车厢货物的13。
2.一条公路,甲队独修24天完成,乙队独修30天完成。
乙队修了10天后甲队继续修还要几天修完?(1-130×10)÷124=16(天) 答:甲队还要修16天修完。
3.一批零件,甲单独做8小时完成,乙单独做7小时完成,现由两人合做,3小时共生产零件225个。
这批零件共有多少个?225÷[(18+17)×3]=280(个) 答:这批零件共有280个。
4.一个游泳池,装有-个进水管和-个出水管,单开进水管10分钟可以将空池放满,单开出水管15分钟可以将满池水放完。
如果将两管同时打开,多少分钟可以将空水池放满?1÷(110-115)=30(分钟) 答:如果将两管同时打开30分钟可以将空水池放满。
三、小强和小若在操场上跑步。
小强跑一圈要5分钟,小若跑一圈要8分钟。
1.如果两人同时同地出发,相背而行,多少分钟后两人相遇?1÷(15+18)=4013(分钟) 答:4013分钟后两人相遇。
2.如果两人同时同地出发,同方向而行,多少分钟后小强超过小若两圈?2÷(15-18)=803(分钟) 答:803分钟后小强超过小若两圈。
《用单位“1”解决实际问题》教案-2021-2022学年数学六年级上册人教版

3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“单位‘1’在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
最后,针对本节课的教学难点和重点,我会继续关注学生的学习进度,不断调整教学方法,力求让每个学生都能真正掌握用单位“1”解决实际问题的方法。同时,我也将鼓励学生们在日常生活中多观察、多思考,将所学知识运用到实际中,提高他们的数学素养。
今天的学习,我们了解了单位“1”的基本概念、重要性和应用。通过实践活动和小组讨论,我们加深了对单位“1”解决实际问题的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。如果有任何疑问或不明白的地方,请随时向我提问。
五、教学反思
今天我们在课堂上一起探讨了《用单位“1”解决实际问题》,回顾整个教学过程,我觉得有几个方面值得反思。
4.激发学生的合作意识,通过小组讨论与交流,培养团队协作解决问题的能力。
5.引导学生体验数学与生活的紧密联系,增强数学学习的兴趣,树立正确的数学观念。
三、教学难点与重点
1.教学重点
(1)理解单位“1”的概念:通过实例让学生明白单位“1”可以表示任何相等的整体,如1个苹果、1米绳子等,以此为基础进行分数的运算。
《用单位“1”解决实际问题》教案-2021-2022学年数学六年级上册人教版
一、教学内容
《用单位“1”解决实际问题》教案-2021-2022学年数学六年级上册人教版。本节课我们将学习以下内容:
1.理解单位“1”的概念,掌握将一个整体平均分成若干份,用分数表示的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、教学目标
(一)知识与技能:掌握用单位“1”解决实际的百分数问题,特别是在没有具体数字的情况下用来解决此类应用题,以达到计算快而准的目标。
(二)过程与方法:通过讨论交流,提高学生运用假设法解决实际问题的能力。
(三)情感态度和价值观:培养学生的抽象思维能力,使学生积累更多解决问题的经验。
二、教学重、难点
重点:掌握用单位“1”解决问题的初步概念。
难点:掌握用单位“1”解决实际的百分数问题。
三、教学准备:课件
四、教学过程
(一)复习导入
找准单位“1”:
1、今年产量比去年多百分之几?
2、这个月用电比上个月节约了百分之几?
3、彩电降价了百分之几?
师:今天我们就来学习用单位“1”解决实际问题。
(板书课题)
(二)探究新知
1.课件出示教学例5,学生试做。
某商品4月的价格比3月降了20%,5月的价格比4月又涨了20%。
5月的价格和3月比是涨了还是降了?变化幅度是多少?
(1)提出问题,寻找解决问题的方法。
师:从中你能获取什么数学信息?
(学生独立阅读并理解题意,从中获得信息)。
(2)在不知道3月具体价格的情况下,我们怎样计算?
(学生以小组为单位讨论,小组代表汇报结果)。
2、讲解探究
方法一:假设此商品3月的价格是100元。
4月价格:100-100×20%=80(元)
5月价格:80+80×20%=96(元)
96元<100元
(100-96)÷100=0.04=4%
发现5月的价格比3月降了4%,是3月的96%。
方法二:将此商品3月的价格看做单位“1”
1×(1-20%)×(1+20%)=0.96
(1-0.96)÷1=0.04=4%
小结:一件未知价格的商品有涨有跌,我们可以假设此商品的价格为“100元”
或者单位“1”,便于我们理解和计算。
3、思维拓展
(1)用字母表示数
假设3月份的价格为a元
4月价格:a﹣a×20%=0.8a
5月价格:0.8a×(1+20%)=0.96a
(a﹣0.96a)÷a=0.04=4%
(三)巩固练习
教学教材练习十九第93页,第11题
(四)课后小结
百分数应用题的解题思路和分数应用题的相同。
关键是找准单位“1”。
单位“1”的量已知,根据求一个数的几分之几是多少用乘法计算。
单位“1”的量未知,可根据等量关系用除法计算。
