手拉手模型
手拉手模型8个结论及证明

手拉手模型8个结论及证明1. 手拉手模型能够提高团队合作能力。
证明:研究表明,通过与他人紧密合作,人们能够更好地理解彼此的需求和目标,从而更好地协调行动,提高团队的整体绩效。
2. 手拉手模型可以促进信息共享和沟通。
证明:在手拉手模型中,成员之间可以更容易地交流和共享信息,避免信息孤岛的情况,从而提高团队的决策质量和效率。
3. 手拉手模型可以增强团队的凝聚力和归属感。
证明:通过手拉手模型,成员之间建立了紧密的联系和互相依赖的关系,从而增强了团队的凝聚力和归属感,提高了团队成员的参与度和投入度。
4. 手拉手模型有助于培养团队成员之间的信任和互相支持。
证明:在手拉手模型中,成员之间需要相互合作和支持,这促使他们建立起信任关系,相信彼此能够共同完成任务,从而提高团队的合作效果。
5. 手拉手模型能够加强团队成员的责任心和承诺感。
证明:在手拉手模型中,每个成员都承担着特定的角色和责任,这促使他们更加重视自己的任务和工作,增强了责任心和承诺感,从而提高了团队的整体表现。
6. 手拉手模型可以促进团队成员之间的学习和成长。
证明:在手拉手模型中,成员之间可以相互学习和分享经验,通过互相观察和模仿,不断提高自己的技能和知识水平,从而促进团队的学习和成长。
7. 手拉手模型能够帮助团队应对挑战和解决问题。
证明:在手拉手模型中,成员之间共同面对困难和挑战,通过相互支持和协作,能够更好地解决问题,提高团队的解决问题的能力和效果。
8. 手拉手模型能够增强团队的创新和创造力。
证明:通过手拉手模型,成员之间能够充分地交流和碰撞思想,从而激发团队的创新和创造力,带来新的想法和解决方案,提高团队的创新能力和竞争力。
全等典型模型:“手拉手”模型

《三角形证明》题型解读12 全等典型模型:“手拉手”模型【知识梳理】(一)“手拉手模型”的基本图形题型特征:△ABC 与△BDE 是等边三角形,A 、B 、D 三点在同一直线上。
解题方法:一定有以下六个结论(三组全等、一个60°、一个等边△、一组平行线) ①△ABE ≌△CBD证明过程:∵△ABC 与△BDE 是等边三角形,∴∠1=∠2=∠3=60°,∴∠ABE=∠CBD=120°,∵AB=BC ,BE=BD , ∴△ABE ≌△CBD (SAS ) ②△ABH ≌△CBF证明过程:∵△ABE ≌△CBD ,∴∠4=∠5,∵AB=BC ,∠1=∠2,∴△ABH ≌△CBF (SAS ) ③△BHE ≌△BFD证明过程:∵△ABE ≌△CBD ,∴∠6=∠7,∵BE=BD ,∠2=∠3,∴△BHE ≌△BFD (SAS ) ④∠AGC=60°证明过程:∵△ABE ≌△CBD ,∴∠6=∠7,在△GFE 和△BFD 中(“8”字模型),∠3=180°-∠BFD-∠7,∠EGF=180°-∠GFE-∠6,∵∠6=∠7,∠GFE=∠BFD ,∴∠3=∠EGF ,∵∠AGC=∠EGF ,∠3=60°,∴∠AGC=∠3=60° ⑤△BHF 是等边三角形证明过程:∵△BHE ≌△BFD (SAS ),∴BH=BF ,∵∠2=60°,∴△BHF 是等边三角形(有一个角是60°的等腰三角形是等边三角形) ⑥HF//AD证明过程:∵△BHF 是等边三角形,∴∠8=60°,∵∠3=60°,∴∠8=∠3,∴HF//AD (二)“手拉手模型”的变化图形题型特征:△ABC 与△BDE 是等边三角形,A 、B 、D 三点不在同一直线上。
图2M N 765431H GFEDCBA765431HG F ED CBA解题方法:一定有以下三个结论(一组全等,一个60°、一个角平分线) ①△ABE ≌△CBD证明过程:∵△ABC 与△BDE 是等边三角形,∴∠1=∠3=60°,∴∠ABE=∠CBD (共角模型),∵AB=BC ,BE=BD , ∴△ABE ≌△CBD (SAS ) ②∠AGC=60°证明过程:∵△ABE ≌△CBD ,∴∠6=∠7,在△GFE 和△BFD 中(“8”字模型),∠3=180°-∠BFD-∠7,∠EGF=180°-∠GFE-∠6,∵∠6=∠7,∠GFE=∠BFD ,∴∠3=∠EGF ,∵∠AGC=∠EGF ,∠3=60°,∴∠AGC=∠3=60° ③BG 平分∠HBF证明过程:作BM ⊥AE 于点M ,BN ⊥GD 于点N ,如图2,∵△ABE ≌△CBD ,∴∠4=∠5,∵AB=BC ,∠AMB=∠CNB=90°,∴△ABM ≌△CBN (AAS ),∴BM=BN ,∴BG 平分∠HBF (到角两边的距离相等的点,在这个角的角平分线上) (三)常见“手拉手”变化图形【典型例题】例1.如图,C 为线段AE 上一动点(不与A 、E 重合),在AE 同侧分别作等边△ABC 和等 边△CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连接PQ ,以下五个结论: ①AD =BE ;②PQ ∥AE ;③CP =CQ ;④BO =OE ;⑤∠AOB =60°,恒成立的结论有( )。
【北师大版】八年级数学专题手拉手几何模型 课件

巩固训练
1.如图,△ABC和△DEC都是等边三角形,点C是它们的公共顶点 求证:AE=BD
2.已知:如图△ABC和△ADE都是等腰直角三角形, ∠BAC=∠DAE=90°. 求证:(1)BD=CE.(2)BD⊥CE
巩固训练
3.如图,△ABD和△BCE是等边三角形,连接AE与CD 求证: (1)△ABE≌△DBC (2)AE=DC (3)AE与DC的夹角为60° (4)AE与DC的交点设为H,BH平分∠AHC
过点b分别往hahc作垂线运用等积法得出两垂线段相等hl判定三角形全等解决4初三时亦可用behc四点共圆证明此结论二发散思维二发散思维例2
初二数学手拉手几何模型
学习目标
1.了解手拉手模型的基本概念 2.掌握手拉手模型的全等与相关结论 3.运用手拉手模型解决实际问题 学习重点: 熟练的找出手拉手模型中的全等三角形及其 相关结论 学习难点: 利用手拉手模型的结论解决问题
(二)发散思维
例2:如图,△ADC和△EDG是等腰直角三角形,连接AG,CE,交 点为H。 (1)证明:△ADG≌△CDE; (2)证明:AG=CE (3)求AG与CE之间的夹角为多少度。 (4)HD是否平分∠AHE?
分析:
等腰直角三角形,两腰相等,两底角相等为45°,其余同例
(三)举一反三
例3:如图,△ADB和△BCE是等腰三角形,其中 AB=BD,CB=EB,∠ABD=∠CBE=α,连接AE与CD,交点为H。 (1)证明:△ABE≌△DBC (2)证明:AE=CD (3)求AE与CD之间的夹角为多少度。 (4)HB是否平分∠AHC?
复习引入
如图,△ABC和△ADE为等腰三角形,其中,∠BAC=∠DAE=α。从中 你能得到哪些结论?
我们重点研究△ABD和△ACE,这两个三 角形是否全等?有哪些边和角对应相等 ?还有什么共同特征?旋转α得到
专题12.19 三角形全等几何模型-“手拉手”模型(知识讲解)
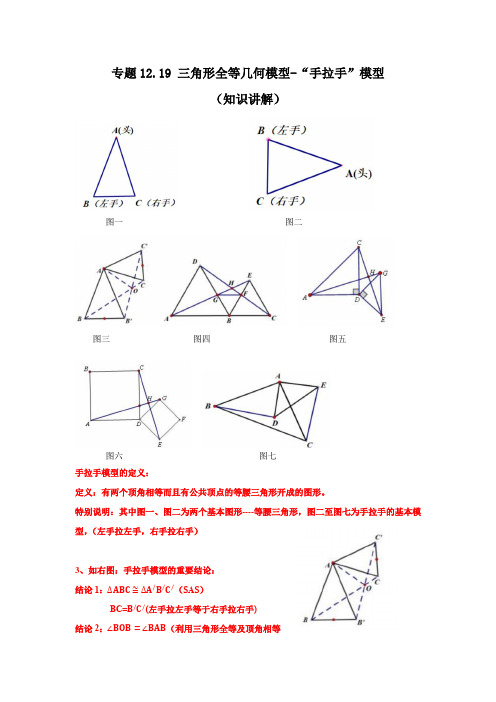
专题12.19 三角形全等几何模型-“手拉手”模型(知识讲解)图一图二图三图四图五图六图七手拉手模型的定义:定义:有两个顶角相等而且有公共顶点的等腰三角形开成的图形。
特别说明:其中图一、图二为两个基本图形----等腰三角形,图二至图七为手拉手的基本模型,(左手拉左手,右手拉右手)3、如右图:手拉手模型的重要结论:结论1:∆ABC≅∆A/B/C/(SAS)BC=B/C/(左手拉左手等于右手拉右手)结论2:∠BOB=∠BAB(利用三角形全等及顶角相等的等腰三角形底角相等)结论3:AO平分∠B O C/(利用三角形全等面积相等,再利用角平分线性质定理证明)典型例题讲练:在学习全等三角形知识时、教学兴趣小组发现这样一个模型:它是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.通过资料查询,他们得知这种模型称为“手拉手模型” 兴趣小组进行了如下操究:(1)如图1、两个等腰三角形△ABC和△ADE中,AB=AC,AE=AD,△BAC=△DAE,连接BD、CE、如果把小等腰三角形的腰长看作小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,这个就是“手拉手模型”,在这个模型中,和△ADB 全等的三角形是,此线BD和CE的数量关系是(2)如图2、两个等腰直角三角形△ABC和△ADE中,AB=AC,AE=AD,△BAC=△DAE=90°,连接BD,CE,两线交于点P,请判断线段BD和CE的数量关系和位置关系,并说明理由:(3)如图3,已知△ABC、请完成作图:以AB、AC为边分别向△ABC外作等边△ABD和等边△ACE(等边三角形三条边相等,三个角都等于60°),连接BE,CD,两线交于点P,并直接写出线段BE和CD的数量关系及△PBC+△PCB的度数、【答案】(1)△AEC,BD=CE;(2)BD=CE且BD△CE,理由见解析;(3)作图见解析,BE=CD,△PBC+△PCB=60°.【分析】(1)根据SAS证明两个三角形全等即可证明;(2)通过条件证明△DAB△△EAC(SAS),得到△DBC+△ECB=90°,即可证明BD△CE,从而得到结果;≅即可得到证明;(3)根据已知条件证明DAC BAE解:(1)△AB=AC,AE=AD,△BAC=△DAE,∠+∠=∠+∠,△DAE EAB BAC EAB即DAB EAC ∠=∠,△()△△ADB AEC SAS ≅,△BD=CE ;(2)BD=CE 且BD△CE ;理由如下:因为△DAE=△BAC=90°,如图2.所以△DAE+△BAE=△BAC+△BAE .所以△DAB=△EAC .在△DAB 和△EAC 中,,,.AD AE DAB EAC AB AC =⎧⎪∠=∠⎨⎪=⎩所以△DAB△△EAC (SAS ).所以BD=CE ,△DBA=△ECA .因为△ECA+△ECB+△ABC=90°,所以△DBA+△ECB+△ABC=90°.即△DBC+△ECB=90°.所以△BPC=180°-(△DBC+△ECB )=90°.所以BD△CE .综上所述:BD=CE 且BD△CE .(3)如图3所示,BE=CD ,△PBC+△PCB=60°.由图可知60DAB EAC ∠=∠=︒,AD=AB ,AE=AC ,△+DAB BAC EAC BAC ∠∠=∠+∠,即DAC BAE ∠=∠,△()△DAE △BAE SAS ≅,△BE=CD ,ABE ADC ∠=∠,又△60BDA ∠=︒,△60ADC BDC ABE BDC ∠+∠=∠+∠=︒,△120BPC ABP BDC BDA ∠=∠+∠+∠=︒,△△PBC+△PCB=60°.【点拨】本题主要考查了全等三角形的知识点应用,准确分析图形是解题的关键. 举一反三变式1:如图,AC △BC ,DC △EC ,AC =BC ,DC =EC ,AE 与BD 交于点F .(1)求证:AE =BD ;(2)求△AFD 的度数.【答案】(1)详情见解析;(2)90AFD ∠=︒【分析】(1)利用角的等量代换求出ACE BCD ∠=∠,再判断ACE ≌BCD △即可求解; (2)利用全等三角形的性质得到E D ∠=∠,再通过角的等量代换求解即可.解:(1)△AC BC ⊥,DC EC ⊥△90ACB ECD ∠=∠=︒△ACB BCE ECD BCE ∠+∠=∠+∠△ACE BCD ∠=∠在ACE 和BCD △中AC BC ACE BCD DC EC =⎧⎪∠=∠⎨⎪=⎩△ACE ≌BCD △(SAS)△AE BD =(2)设BD 与CE 的交点为G ,如图所示:△ACE ≌BCD △△E D ∠=∠△180EFG FGE E ++=︒∠∠∠,180GCD CGD D ++=︒∠∠∠,且BGE CGD ∠=∠△90EFG GCD ==︒∠∠△90AFD ∠=︒【点拨】本题主要考查了全等三角形的性质和判定,灵活运用角的等量代换是解题的关键.例题2.已如:如图1,B ,C ,D 三点在一条直线上,△ABC 和△ECD 均为等边三角形,连接BE ,AD 交于点F ,BE 交AC 于点M ,AD 交CE 于点N .(1)以下结论正确的有 ;△AD =BE △△EFD =60° △MC =NC △△AMB =△END(2)探究:将图1中的△ECD 绕点C 顺时针旋转一个角度(旋转角小于60°),如图2所示. △问:(1)中的正确结论哪些还成立?若成立,请说明理由;△连接FC ,如图3所示,求证:FC 平分△BFD【答案】(1)△△△;(2)△ △△;△见解析.【分析】(1)△根据等边三角形的性质得CA =CB ,CD =CE ,△ACB =60°,△DCE =60°,则△ACE =60°,利用“SAS ”可判断△ACD △△BCE ,则AD =BE ;△根据三角形外角关系得△EFD =△EBC +△ADC =△DAC +△ADC =△ACB =60°,从而可得结论; △连接MN ,证明△MCN 是等边三角形即可得出结论;△60,60AMB EBC END NDC ∠=︒+∠∠=︒+∠,而AC ≠CD 得CAD CDA ∠≠∠,从而可得出结论;(2)△方法同(1),逐个结论进行证明即可;△作,CG BE CH AD ⊥⊥于点G ,H ,证明△BGC △△AHC ,△CGF △△CHF 可得△CFG CFH =∠,从而可得结论.解:(1)△△ABC ,△ECD 是等边三角形,△AC=BC ,CE=CD ,△ACB=△ECD=60°△△ACD=△BCE=△120°△△ACD△△BCE△AD=BE ,故△正确;△△FEN=△NDC又△△ENF=△CND△△EFD=△ECD=60°,故△正确;又△△ACE=△NCD=60°△MEC=△NDCEC=CD△△EMC△△DNC△MC=NC ,故△正确;又△△AMB=△ACB+△ECB=60°+△ECB ,△END=△ECD+△NDC=60°+△NDC而AC CD ≠△CAD CDA ∠≠∠△MBC NDC ∠≠∠△MBC END ∠≠∠,故△错误;故答案为:△△△;(2)△△ACB=△ECD=60°△△BCE=△ACD又AC=BC ,CE=CD△△ACD△△BCE△AD=BE,故△正确;△△ADC=△BEC又△ENF=△CND△△EFD=△ECD=60°,故△正确△△ACE≠60°=△ECD△△EMC 不全等于△DNC ,△MC≠NC ,故△错误(3),CG BE CH AD ⊥⊥于点G ,H ,如图,由(2)△知,△CBG=△CAHAC=BC△BGC=△AHC=90°△△BGC△△AHC△CG=CH又CF=CF ,△CGF=△CHF=90°△△CGF△△CHF△△CFG=△CFH△FC 平分△BFD【点拨】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS ”、“SAS ”、“ASA ”、“AAS ”;全等三角形的对应边相等.也考查了等边三角形的判定与性质.举一反三变式:如图,在ABC∆中,分别以AC,BC为边作等边三角形ACD和等边三角形BCE,连接AE,BD交于点O,则AOB∠的度数为()A.100︒B.120︒C.130︒D.150︒【答案】B【分析】先证明△DCB△△ACE,求出△CAE=△CDB,再利用“8字型”证明△AOH=△DCH =60°即可解决问题.解:如图:AC与BD交于点H,△△ACD,△BCE都是等边三角形,△CD=CA,CB=CE,△ACD=△BCE=60°,△△DCB=△ACE,在△DCB和△ACE中,CD CADCB ACECB CE⎧⎪∠∠⎨⎪⎩===,△△DCB△△ACE,△△CAE=△CDB,△△DCH+△CHD+△BDC=180°,△AOH+△AHO+△CAE=180°,△DHC=△OHA,△△AOH=△DCH=60°,△△AOB=180°−△AOH=120°.故选:B.【点拨】本题考查全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是正确寻找全等三角形,学会利用“8字型”证明角相等,属于中考常考题型.例题3.(阅读材料)小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若△BAC=△DAE,AB=AC,AD=AE,则△ABD△△ACE.(材料理解)(1)在图1中证明小明的发现.(深入探究)(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:△BD=EC;△△BOC=60°;△△AOE=60°;△EO=CO,其中正确的有.(将所有正确的序号填在横线上).(延伸应用)(3)如图3,AB=BC,△ABC=△BDC=60°,试探究△A与△C的数量关系.【答案】(1)证明见解析;(2)△△△;(3)△A+△C=180°.【分析】(1)利用等式的性质得出△BAD=△CAE,即可得出结论;(2)同(1)的方法判断出△ABD△△ACE,得出BD=CE,再利用对顶角和三角形的内角和定理判断出△BOC=60°,再判断出△BCF△△ACO,得出△AOC=120°,进而得出△AOE=60°,再判断出BF<CF,进而判断出△OBC>30°,即可得出结论;(3)先判断出△BDP是等边三角形,得出BD=BP,△DBP=60°,进而判断出△ABD△△CBP(SAS ),即可得出结论.(1)证明:△△BAC=△DAE ,△△BAC+△CAD=△DAE+△CAD , △△BAD=△CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩=== ,△△ABD△△ACE ;(2)如图2,△△ABC 和△ADE 是等边三角形, △AB=AC ,AD=AE ,△BAC=△DAE=60°, △△BAD=△CAE ,在△ABD 和△ACE 中,AB AC BAD CAE AD AE ⎧⎪∠∠⎨⎪⎩=== ,△△ABD△△ACE ,△BD=CE ,△正确,△ADB=△AEC , 记AD 与CE 的交点为G ,△△AGE=△DGO ,△180°-△ADB -△DGO=180°-△AEC -△AGE , △△DOE=△DAE=60°,△△BOC=60°,△正确,在OB上取一点F,使OF=OC,△△OCF是等边三角形,△CF=OC,△OFC=△OCF=60°=△ACB,△△BCF=△ACO,△AB=AC,△△BCF△△ACO(SAS),△△AOC=△BFC=180°-△OFC=120°,△△AOE=180°-△AOC=60°,△正确,连接AF,要使OC=OE,则有OC=12 CE,△BD=CE,△CF=OF=12 BD,△OF=BF+OD,△BF<CF,△△OBC>△BCF,△△OBC+△BCF=△OFC=60°,△△OBC>30°,而没办法判断△OBC大于30度,所以,△不一定正确,即:正确的有△△△,故答案为△△△;(3)如图3,延长DC至P,使DP=DB,△△BDC=60°,△△BDP 是等边三角形,△BD=BP ,△DBP=60°,△△BAC=60°=△DBP ,△△ABD=△CBP ,△AB=CB ,△△ABD△△CBP (SAS ),△△BCP=△A ,△△BCD+△BCP=180°,△△A+△BCD=180°.【点拨】此题考查三角形综合题,等腰三角形的性质,等边三角形的性质,全等三角形的判定和性质,构造等边三角形是解题的关键.举一反三变式:如图,C 为线段AE 上一动点(不与点,A E 重合),在AE 同侧分别作等边三角形ABC 和等边三角形,CDE AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ .以下结论:①AD BE =;①//PQ AE ;①60AOB ∠=︒;①CPQ 是等边三角形,恒成立的是______.【答案】△△△△【分析】△由△ABC 和△CDE 都是等边三角形,可知AC=BC ,CD=CE ,△ACB=△DCE=60°,所以△ACD=△BCE=120°,所以△ACD△△BCE (SAS ),从而AD=BE ,故△正确;△△由△ACD△△BCE 得△CBE=△DAC ,加之AC=BC ,易得△ACB=△BCQ=60°,可证△CQB△△CPA (ASA ),从而CP=CQ ,再加之△PCQ=60°,可推出△PCQ 为等边三角形,易得△PQC=60°=△DCE ,根据内错角相等,两直线平行,可知△△正确;△结合△ACD△△BCE 和三角形的外角的性质,可得△AOB=60°,故△正确.解:△△等边△ABC 和等边△CDE ,△AC=BC ,CD=CE ,△ACB=△DCE=60°,△△ACB+△BCD=△DCE+△BCD ,即△ACD=△BCE ,△在△ACD 与△BCE 中,AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===△△ACD△△BCE (SAS ),△AD=BE ,故△正确;△△△△ACD△△BCE ,△△CBE=△DAC ,△由△ACB=△DCE=60°得△BCD=60°,△△ACP=△BCQ ,又△AC=BC ,△△CQB△△CPA (ASA ),△CP=CQ ,又△△PCQ=60°△△PCQ 为等边三角形,△△PQC=60°,△△PQC=60°=△DCE△PQ△AE故△△正确;△△△ACD△△BCE (SAS ),△△CAD=△CBE ,△△AOB=△CAD+△CEB=△CBE+△CEB ,又△△ACB=△CBE+△CEB=60°,△△AOB=△ACB=60°,故△正确.故答案为:△△△△.【点拨】本题考查了等边三角形的性质、全等三角形的判定与性质、三角形外角的性质,熟练应用三角形全等的判定是解题的关键.。
(完整版)计算机模型手拉手模型

(完整版)计算机模型手拉手模型1. 模型简介计算机模型手拉手模型是一种基于计算机科学的模型,用于描述计算机系统中各个组件之间的相互协作和通信方式。
该模型的设计灵感源自实际生活中的手拉手,形象地展示了计算机系统中各个组件之间通过通信协议进行数据交互的过程。
2. 模型结构计算机模型手拉手模型由以下几个主要组成部分构成:2.1. 手拉手接口手拉手接口是模型的核心部分,它通过模拟计算机系统中的通信协议,实现不同组件之间的连接和数据传输。
手拉手接口包含了发送和接收数据的功能,以及数据传输的控制逻辑。
2.2. 组件模块模型中的每个组件模块代表了计算机系统中的一个具体组件,例如CPU、内存、硬盘等。
每个组件模块都通过手拉手接口与其他组件进行连接,实现数据的传输和协作。
2.3. 数据线数据线是模型中的另一个重要部分,它用于在不同组件之间传输数据。
数据线不仅连接了不同组件的手拉手接口,还承载了数据的传输和传递。
3. 模型原理计算机模型手拉手模型的原理是模拟计算机系统中的数据交互过程。
当一个组件需要与另一个组件进行数据交换时,它会通过手拉手接口将数据发送给对应的组件。
接收组件收到数据后,会进行相应的处理,并通过手拉手接口将处理结果返回给发送组件。
模型通过手拉手接口和数据线的连接实现了组件之间的通信和协作。
数据线的拓扑结构可以灵活地调整,以适应不同计算机系统的需求。
4. 应用场景计算机模型手拉手模型可以被广泛应用于计算机科学领域的教学和研究工作中。
通过模型,学生可以直观地了解计算机系统中各个组件之间的数据交互方式,加深对计算机系统原理的理解。
此外,这个模型还可以作为一种通信协议的教学工具,帮助学生更好地理解通信协议的原理和实现方式。
5. 结论计算机模型手拉手模型通过形象生动的手拉手形态,展示了计算机系统中各个组件之间的通信和协作方式。
它可以被广泛应用于计算机科学教学和研究领域,有助于提升学生对计算机科学原理的理解和应用能力。
手拉手模型的判定方法

手拉手模型的判定方法摘要:一、手拉手模型概述二、手拉手模型的判定方法1.视觉判定2.力学判定3.动力学判定4.神经网络判定三、各类判定方法的优缺点对比四、手拉手模型在实际应用中的案例分析五、未来发展趋势与展望正文:一、手拉手模型概述手拉手模型,是一种模拟人类行走、跑步等动态行为的机器人运动模型。
通过模拟人类运动过程中的关节运动、肌肉收缩等生理现象,实现机器人的自主运动。
手拉手模型在机器人研究领域具有广泛的应用价值,为研究人类行走提供了有力的理论支持。
二、手拉手模型的判定方法1.视觉判定视觉判定方法主要通过分析摄像头或其他图像传感器捕捉到的图像,对机器人运动状态进行判断。
该方法依赖于图像处理技术的发展,具有较高的实时性和准确性。
但同时,受到光照、遮挡等因素的影响,视觉判定方法在实际应用中存在一定局限性。
2.力学判定力学判定方法通过对机器人运动过程中的力学参数进行监测和分析,如加速度、速度、力等,判断机器人是否达到手拉手模型。
该方法具有较高的理论依据,但测量设备和算法的要求较高,实现难度相对较大。
3.动力学判定动力学判定方法结合机器人的动力学模型,通过计算运动学参数与动力学参数之间的关系,判断机器人是否符合手拉手模型。
该方法对机器人结构和运动学参数有较高要求,但在理论分析方面具有较好的优势。
4.神经网络判定神经网络判定方法利用已训练好的神经网络模型,对机器人运动状态进行判定。
该方法具有较强的适应性和鲁棒性,能够应对各种复杂环境。
但神经网络模型的训练过程较为复杂,需要大量数据支持。
三、各类判定方法的优缺点对比1.视觉判定:优点在于实时性强、准确性高,但受光照、遮挡等因素影响;2.力学判定:理论依据充分,但对测量设备和算法要求较高;3.动力学判定:对机器人结构和运动学参数有较高要求,但在理论分析方面具有优势;4.神经网络判定:适应性强、鲁棒性好,但训练过程较为复杂,需要大量数据支持。
四、手拉手模型在实际应用中的案例分析手拉手模型在机器人领域的应用案例丰富,如无人驾驶汽车、四足机器人、人形机器人等。
(完整版)经济模型手拉手模型

(完整版)经济模型手拉手模型经济模型手拉手模型摘要经济模型手拉手模型是一种有效的经济合作模式,通过形成紧密的合作网络,促进经济发展和资源共享。
本文介绍了经济模型手拉手模型的概念、特点和实施步骤,并分析了其在促进区域发展、促进企业合作和提高经济效益等方面的优势。
1. 概念经济模型手拉手模型是指在一个区域或一个领域内,不同经济主体之间建立紧密的合作网络,通过共享资源、互相支持和合作创新,实现经济共同发展的模式。
2. 特点- 多方参与:经济模型手拉手模型中涉及的经济主体包括政府、企业、高校、科研机构等多个方面,形成了多方参与的格局。
- 资源共享:通过合作,不同经济主体可以共享资源,推动优势互补,提高资源的利用效率。
- 提供支持:经济模型手拉手模型鼓励不同经济主体间互相支持,通过技术转移、创新合作等方式提供支持,促进经济发展。
- 创新推动:经济模型手拉手模型注重合作创新,通过共同研发、技术转移等方式推动科技进步和产业升级。
3. 实施步骤实施经济模型手拉手模型需要以下步骤:1. 建立联盟:各经济主体共同协商组成联盟,明确联盟的目标和任务。
2. 制定合作方案:根据各方的资源和需求,制定合作方案,明确合作的领域和方式。
3. 共享资源:各方通过资源共享,实现优势互补,提高资源的利用效率。
4. 支持合作:各方提供技术支持、资金支持等形式的合作支持,推动合作项目的顺利进行。
5. 评估调整:不断评估合作效果,及时调整合作方案,确保合作模式的有效运行。
4. 优势和意义经济模型手拉手模型在促进区域发展、促进企业合作和提高经济效益方面具有以下优势和意义:- 提升区域竞争力:通过合作创新和资源共享,能够提升整个区域的经济竞争力。
- 促进企业合作:不同企业之间可以共享资源,加强合作,促进企业发展和规模扩大。
- 提高经济效益:通过合作创新和资源共享,可以提高资源的利用效率,提升经济效益。
- 推动科技进步:合作创新能够促进科技的进步和产业的升级,推动经济发展。
(完整版)社会学模型手拉手模型

完整版)社会学模型手拉手模型1.引言社会学是研究人类社会行为、社会关系和社会机构的科学。
手拉手模型是社会学中一个重要的概念,用来描述人们在社会互动中相互协作、互惠互助的关系。
本文将介绍手拉手模型的定义、特点和应用,并探讨其在社会学研究中的意义和影响。
2.手拉手模型的定义手拉手模型是指人们在社会交往中通过相互支持、合作和互助,形成紧密的互联互动的关系。
它强调人与人之间的互惠和互助,是一种相互关联和相互依赖的社会联系模式。
3.手拉手模型的特点手拉手模型具有以下几个特点:相互支持:手拉手模型强调人们在社会交往中相互支持,通过共同的努力和帮助来实现目标。
合作互助:在手拉手模型中,人们通过相互合作和互助,共同解决问题和应对挑战。
互联互动:手拉手模型强调人与人之间的紧密联系和互动,通过交流和合作实现共同的利益。
4.手拉手模型的应用手拉手模型在社会学研究中有广泛的应用,例如:教育领域:手拉手模型可以用于描述学生之间的相互支持和合作学习的关系,促进学生的共同学习和发展。
社区发展:手拉手模型可以应用于社区组织和发展,通过组织居民之间的互助、合作和支持,提高社区的凝聚力和发展能力。
心理健康:手拉手模型可以用于描述亲密关系中的相互支持和互助,帮助个体在压力和困难时获得支持和帮助。
5.手拉手模型的意义和影响手拉手模型的应用和研究对社会学具有重要意义和积极影响:加强社会联系:手拉手模型强调人与人之间的相互关联和互助,可以加强社会联系和社区凝聚力。
促进社会发展:通过手拉手模型中的合作和互助,可以促进社会的发展和进步。
改善人际关系:手拉手模型强调相互支持和互助,有助于改善人际关系和促进个体的心理健康。
6.结论手拉手模型是社会学中的一个重要概念,用于描述人们在社会交往中相互协作、互惠互助的关系。
它强调人与人之间的相互支持、合作和互助,在教育、社区发展和心理健康等领域有广泛的应用。
手拉手模型的研究和应用对于加强社会联系、促进社会发展和改善人际关系具有重要意义和积极影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等找
△ACE≌△BC D
1、识别: 顶角相等的等腰三角形,顶点相同 2、步骤: 等边、等角、全等找(大手拉小手)
如图,点 C 是线段 BD 上一点,以 BC,CD 分别为腰作等腰 △ABC 和
等腰 △CDE,且∠ACB = ∠ECD = α,连接 BE 和 AD 交于点O.
(1)求证:BE = AD;
(2)求∠AOB 的度数 .
等边 等角 全等找
(1)△ACD≌△BCE (2)∠AOB=∠ACB =∠ECD=α 第三边夹角=顶角
我们发现:
(1)△ACD≌△BCE
(2)∠AOB=∠ACB 第三边夹角=顶角
如图1,△ABC 和 △CDE 均为等腰直角三角形,连接 BE ,AD 交于点 F . (1)求证: △BCE≌ △ACD ;(2)求∠AFB 的度数; (3)若 △CDE 转动到图 2 位置时,延长 BE 交 AD 于点 F,∠AFB 度数
(2)分别延长 AD,BE 交于点 F,求∠AFB 的度数
(1)△BEC≌△ADC
(2)∠AFB=60°
第三边夹角=顶角
F
手 拉
等腰
手
学习目标:
1、认识并学会识别手拉手模型
2、掌握手拉手模型的证明
3、学会运用手拉手模型解题
What is 手拉手?
Ⅰ 顶角相等的两个等腰三角形
Ⅱ 顶点相同
01
常规手拉手
A
D
等边 等角
E
B
C
△ABC 和△CDE 是等边三角形
△ACE≌△BCD
全等找
02
A
多动手拉手
D
E
等边 等角
B
C
△ABEC≌△ADC
(2)∠AFB=90° 第三边夹角=顶角
F
F
总结:
1、识别: 顶角相等的等腰三角形,顶点相同 2、步骤: 等边、等角、全等找(大手拉小手)
3、重要结论: ① △ACD≌△BCE
② ∠AOB=∠ACB(底边夹角=顶角)
△ABC 和 △CDE 均为等边三角形,连接 BE ,AD . (1)求证:BE = AD;
