叠加法求梁的位移【PPT】共21页文档
合集下载
16第十六讲(叠加法计算梁的位移)
利用附录IV中，1、2、4、6、7、8、10简单结构和荷载时的 挠度和转角，计算复杂结构和荷载作用下的挠度和转角。
三峡大学 工程力学系
材料力学教案
第十六讲：弯曲位移的叠加法
例题 试按叠加原理求图a所示等直梁的跨中截面挠度 wC
和两支座截面的转角qA 及 qB。
(a)
解：此梁 wC 及qA，qB 实际上可不按叠加原理而直接
弯曲位移的叠加法注意到反对称荷载作用下跨中截面不仅挠度为零而且该在集度为q2的反对称均布荷载作用下由于挠曲线也是与跨中截面反对称的故有02?cwc三峡大学工程力学系截面上的弯矩亦为零但转角不等于零因此可将左半跨梁ac和右半跨梁cb分别视为受集度为q2的均布荷载作用而跨长为l2的简支梁
材料力学教案 上一讲我们学到
C
在集度为q/2的正对称均布荷载作用下，利用本教材 附录Ⅳ表中序号8的公式有
5q/2l4 5q4l
w C 138 E4I76 E8 I
qA1q 2/2 E 4l3I4qE 8 3lI qB 1q 2/2 E 4 l3I4qE 3 8lI
三峡大学 工程力学系
材料力学教案
C
第十六讲：弯曲位移的叠加法
三峡大学 工程力学系
材料力学教案
第十六讲：弯曲位移的叠加法
图b所示悬臂梁AB的受力情况与原外伸梁AB段相同， 但要注意原外伸梁的B支座截面是可以转动的，其转角就是
上面求得的qB，由此引起的A端挠度w1=|qB|·a应叠加到图b
所示悬臂梁的A端挠度w2上去才是原外伸梁的A端挠度wA：
w A w1 w2
在集度为q/2的反对称均布荷 载作用下，由于挠曲线也是与跨 中截面反对称的，故有
wC2 0 注意到反对称荷载作用下跨中截面不仅挠度为零，而且该
三峡大学 工程力学系
材料力学教案
第十六讲：弯曲位移的叠加法
例题 试按叠加原理求图a所示等直梁的跨中截面挠度 wC
和两支座截面的转角qA 及 qB。
(a)
解：此梁 wC 及qA，qB 实际上可不按叠加原理而直接
弯曲位移的叠加法注意到反对称荷载作用下跨中截面不仅挠度为零而且该在集度为q2的反对称均布荷载作用下由于挠曲线也是与跨中截面反对称的故有02?cwc三峡大学工程力学系截面上的弯矩亦为零但转角不等于零因此可将左半跨梁ac和右半跨梁cb分别视为受集度为q2的均布荷载作用而跨长为l2的简支梁
材料力学教案 上一讲我们学到
C
在集度为q/2的正对称均布荷载作用下，利用本教材 附录Ⅳ表中序号8的公式有
5q/2l4 5q4l
w C 138 E4I76 E8 I
qA1q 2/2 E 4l3I4qE 8 3lI qB 1q 2/2 E 4 l3I4qE 3 8lI
三峡大学 工程力学系
材料力学教案
C
第十六讲：弯曲位移的叠加法
三峡大学 工程力学系
材料力学教案
第十六讲：弯曲位移的叠加法
图b所示悬臂梁AB的受力情况与原外伸梁AB段相同， 但要注意原外伸梁的B支座截面是可以转动的，其转角就是
上面求得的qB，由此引起的A端挠度w1=|qB|·a应叠加到图b
所示悬臂梁的A端挠度w2上去才是原外伸梁的A端挠度wA：
w A w1 w2
在集度为q/2的反对称均布荷 载作用下，由于挠曲线也是与跨 中截面反对称的，故有
wC2 0 注意到反对称荷载作用下跨中截面不仅挠度为零，而且该
04-8.3 叠加法求梁的位移
BC段弹性曲引起 wCF (↓)
结果:
wC
wCF
B
a
2qa4 3EI
注意：引起 θB的有两项 —— q 和qa2，他们的转向不同，叠加时注意正负号
梁的刚度校核
梁的设计：——利用强度条件设计，利用刚度条件校核
刚度条件：
wmax l
w l
max
w 精密机床主轴 l 吊车梁
土建
1 5000
三、方法
1.分解——每种情况都是简单模型 2.分别计算——查表 3.叠加
简单模型 ——悬臂梁
Me
l
A
A
Mel EI
wA
Mel 2 2EI
F
l
A
A
Fl 2 2EI
wA
Fl 3 3EI
q
A
A
ql 3 6EI
ql 4
wA
8EI
l
简单模型 —— 简支梁
F
A
l
C
l
B
A
Fl 2 16EI
wBF
F( l2)3 3EI
Fl 3 24EI
B
F ( l 2)2 2EI
Fll 2
wCM 2EI
结果：
wC
w BF
B
l 2 wCMe
19Fl 3 48EI
例题 3
q A
2a
已知：EI=常数，求wC
qa
q
B
CA
a
2a
qa
θB B qa2
a
qa
B
C
wCF
a
分析：AB段B截面转角引起 θB a （↑）
B
wCF
2. 分别计算
结构力学 叠加法
2．6叠加法作弯矩图当梁在荷载作用下变形微小，因而在求梁的支反力、剪力、弯矩时可直接代入梁的原始尺寸进行计算，且所得结果与梁上荷载成正比。
在这种情况下，当梁上有几项荷载作用时，由每一项荷载所引起的梁的支反力或内力，将不受其他荷载的影响。
所以在计算梁的某截面上的弯矩时，只需先分别算出各项荷载单独作用时在该截面上引起的弯矩，然后求它们的代数和即得到该截面上的总弯矩。
这种由几个外力共同作用引起的某一参数(内力、位移等)等于每一外力单独作用时引起的该参数值的代数和的方法，称为叠加法。
叠加法的应用很广，它的应用条件是：需要计算的物理量(如支反力、内力以及以后要讨论的应力和变形等)必须是荷载的线性齐次式。
也就是说，该物理量的荷载表达式中既不包含荷载的一次方以上的项，也不包含荷载的零次项。
例题2-9试按叠加原理做例题2-9图(a)所示简支梁的弯矩图。
求梁的极值弯矩和最大弯矩。
解：先将梁上每一项荷载分开(见图(b)、图(c))，分别做出力偶和均布荷载单独作用的弯矩图(见图(d)、图(e))两图的纵坐标具有不同的正负号，在叠加时可把它们画在x 轴同一侧(见图f)。
于是两图共有部分，其正、负纵坐标值互相抵消。
剩下的纵距(见图(f)中阴影线部分)即代表叠加后的弯矩值。
叠加后的弯矩图仍为抛物线。
如将它改画为以水平直线为基线的图，即得通常形式的弯矩图(见图(曲)。
求极值弯矩时，先要确定剪力为零的截面位置。
由平衡方程0Bm =∑可求得支反,剪力方程为Q 即可求出极值弯矩所在截面的位置。
令()0x极值弯矩为由例题2-9图（g)可见，全梁最大弯矩为本例中的极值弯矩并不大于梁的最大值弯矩。
当梁上的荷载较复杂时，也可将梁按荷载情况分段，求出每一段梁两端截面的内力。
这时该段梁的受载情况等效于一受相同荷载的简支梁 (见图2-12(a)、(b))。
因为每一段梁在平面弯曲时的内力，不外是轴力N、剪力Q和弯矩M。
由于轴力N不产生弯矩，故在作弯矩图时可将它略去，剩下的梁端剪力1Q，2Q和梁端弯矩1M、2M，及荷载对梁段的作用，可用图2-12(b)所示的简支梁上相应的荷载来代替(梁段端截面上的剪力可由梁的支反力提供，故图中未画出)。
第五章梁弯曲时的位移含能量法教学优秀PPT
l
）
wm axwxl 2
358qE4l4 I（↓）
★转角为正时，表示其转向和由x轴转向y轴的时针相
同；挠度为正时，表示其方向和y轴正向相同。
例2.已知梁的抗弯刚度为EI。试求图示悬臂梁 在集中力P作用下的转角方程、挠曲线方程， 并确定θmax和wmax。
y
P
A l
Bx
解：M (x)P (lx) y
解：因BC弯曲刚度无穷大，只要对AC段考虑
M(x) Fx 2
x [0, l ] 2
x
A
E1I1
l
F
E1I2 B Cl
ΔCy
l 2 0
M(x) E1I1
M(x) dx
F
2
2
l 2
F1
96E1I1
Ⅲ、单位力法（单位载荷法）
对于梁,弯矩应用完全叠加法表示
M ( x ) F 1 M 1 ( x ) F iM i( x ) F n M n ( x )
连续光滑曲线(A、B处转角、挠度唯一）
边界条件
固定端约束对位移的影响：B处转角、挠 度?
连续光滑曲线
例1.已知梁的抗弯刚度为EI。试求图示简 支梁在均布载荷q作用下的转角方程、挠 曲线方程，并确定θmax和wmax。
y
q
x
l
解：M(x)qlxqx2 y
22
q
Ew I q lxqx2 22
A
B
x
Ew Iqlx2qx3C
x
l
46
EIw qlx3qx4C xD 12 24
由边界条件：x 0时 ，w0
x l时 ，w0
得：
Cql3 ,D0 24
w q (6lx 24x3l3)
材料力学梁的弯曲变形第3节 用叠加法求梁的变形
挠曲轴线 近似微分方程
y M (x) EI
• 叠加原理：当梁为小变形时，梁的挠度和转角均是 载荷的线性函数，可以使用叠加法计算梁的转角和 挠度，即梁在几个载荷同时作用下产生的挠度和转 角等于各个载荷单独作用下梁的挠度和转角的叠加 和，这就是计算梁弯曲变形的叠加原理。
• 叠加原理的步骤： ①分解载荷；②分别计算各载荷 单独作用时梁的变形；③叠加得最后结果。
a
x
5ql 4 384 EI
例6-5 悬臂梁AB上作用有均布载荷q，自由端作 用有集中力F = ql，梁的跨度为l，抗弯刚度为EI，如 图所示。试求截面B的挠度和转角。
解：（1）分解载荷
梁上载荷可分解成均布载 荷 q 与集中力 F 的叠加。
（2）查表得这两钟情况下
截面 B 的挠度和转角
yBq
ql3 2EI
2ql
3
（顺时针）
3EI
例6-6 如图所示，外伸梁在外伸段作用有均布 载荷q，梁的抗弯刚度为EI。求C截面的挠度。
解： 1）简化、分解载荷
2）分别计算 B 截面挠度：
悬臂梁因 B 截面产生转角引
起的挠度 yC1和悬臂梁在均布 载荷作用下产生的挠度 yC2
0.5qa2
qa
+
B
yA3
ql4 8EI
7ql 4 384EI
5Fl3 48EI
41ql4 5Fl3 384EI 48EI
代入数值得：
yA 3.89 103 m 3.89mm（）
ql 4 8EI
+
Bq
ql3 6EI
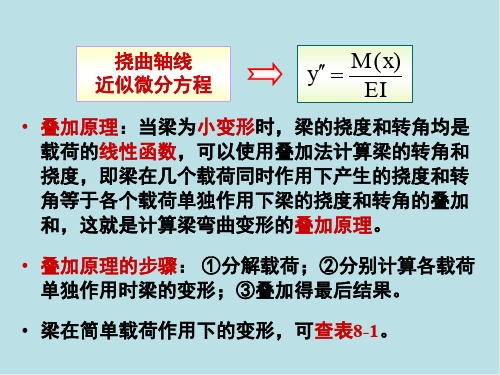
y M (x) EI
• 叠加原理：当梁为小变形时，梁的挠度和转角均是 载荷的线性函数，可以使用叠加法计算梁的转角和 挠度，即梁在几个载荷同时作用下产生的挠度和转 角等于各个载荷单独作用下梁的挠度和转角的叠加 和，这就是计算梁弯曲变形的叠加原理。
• 叠加原理的步骤： ①分解载荷；②分别计算各载荷 单独作用时梁的变形；③叠加得最后结果。
a
x
5ql 4 384 EI
例6-5 悬臂梁AB上作用有均布载荷q，自由端作 用有集中力F = ql，梁的跨度为l，抗弯刚度为EI，如 图所示。试求截面B的挠度和转角。
解：（1）分解载荷
梁上载荷可分解成均布载 荷 q 与集中力 F 的叠加。
（2）查表得这两钟情况下
截面 B 的挠度和转角
yBq
ql3 2EI
2ql
3
（顺时针）
3EI
例6-6 如图所示，外伸梁在外伸段作用有均布 载荷q，梁的抗弯刚度为EI。求C截面的挠度。
解： 1）简化、分解载荷
2）分别计算 B 截面挠度：
悬臂梁因 B 截面产生转角引
起的挠度 yC1和悬臂梁在均布 载荷作用下产生的挠度 yC2
0.5qa2
qa
+
B
yA3
ql4 8EI
7ql 4 384EI
5Fl3 48EI
41ql4 5Fl3 384EI 48EI
代入数值得：
yA 3.89 103 m 3.89mm（）
ql 4 8EI
+
Bq
ql3 6EI
用叠加法计算梁的变形
2 3
由 U W得
Pl vB 3EI
3
作业：5-18，5-19，6-15©,6-18
谢谢大家!
目录
下章 结束
3
θB2
P Pa
f c f c1 f c 2
pa PaL fc a 3EI 3EI
[例8-4]：欲使AD梁C点挠度为零，求P与q的关
系。
CL9TU23
解：
5q(2a) wC 384EI 5 P qa 6
4
Pa(2a) 16EI
2
0
[例8-5] 用叠加法求图示梁Ｃ端的转角和挠度
三. 梁的刚度条件
机械：1/5000~1/10000,
土木：1/250~1/1000 机械：0.005~0.001rad
[w]、[θ ]是构件的许可挠度和转角，它们决定于 构件正常工作时的要求。 [例8-8]图示工字钢梁，l =8m，Iz=2370cm4,Wz=237cm3， [ w/L ]= l／500，E=200GPa，[σ ]=100MPa。试根据梁 的刚度条件，确定梁的许可载荷 [P]，并校核强度。
。
CL9TU29
[例8-6]求图示梁B、D两处的挠度 vB、 vD
。
CL9TU26
[解]
qa 2a 2 qa (2a ) 2 B 3EI 16 EI 3 qa 顺时针 12 EI
2
C
qa qa B 6 EI 4 EI
4
3
3
顺时针
4
qa 5qa wC B a 8EI 24EI
逐段刚化法：
变形后AB部分为曲线， 但BC部分仍为直线。 变形后：AB AB` BC B`C`
工程力学第20讲 弯曲变形：计算梁位移的叠加法
梁的合理刚度设计
横截面形状的合理选择
使用较小的截面面积 A，获得较大惯性矩 I 的截面形 状，例如工字形与盒形等薄壁截面
材料的合理选择
影响梁刚度的力学性能是 E ，为提高刚度，宜选用E 较高的材料
注意：各种钢材（或各种铝合金）的 E 基本相同
钢与合金钢： (200 ~ 220) GPa E 铝 合 金：E (70 ~ 72) GPa
3
FBy l 3
Fy 0, 得 FA y 11F / 16
－平衡方程
综合考虑三方面
分析方法与步骤
判断梁的静不定度 用多余力 代替多余约束
的作用，得受力与原静不定 梁相同的静定梁－相当系统 注意: 相当系统有多种选择 计算相当系统在多余约 束处的位移，并根据变形 协调条件建立补充方程
w max d
d －许用挠度 q －许用转角
l l ~ 750 500 3l 5l ~ 10000 10000
q max q
桥式起重机梁： d
一般用途的轴： d
指定截面的位移控制
w d
q q
例如滑动轴承处: q 0.001 rad
解：
M max
Fl 4
Fl M max Wz 4[s ] [s ]
Wz 2.19 104 m3
Fl 3 d max 48 EI z l d max Fl 2 l 48 EI z 500 500Fl 2 2.92 105 m4 Iz 48 E
-4 3 -5 4 选№22a Wz 3.09 10 m ， I z 3.40 10 m
3
当梁上作用几个载荷时，任一横截面 的总位移，等于各载荷单独作用时在 该截面引起的位移的代数和或矢量和
工程力学梁的变形教学PPT
Fbl 2 16 EI
0.0625
Fbl 2 EI
26
可见在集中荷载作用于右支座附近这种极端情况下，跨中
挠度与最大挠度也只相差不到3%。因此在工程计算中，只要 简支梁的挠曲线上没有拐点都可以跨中挠度代替最大挠度。
当集中荷载F作用于简支梁的跨中时(b=l/2)，最大转角
qmax和最大挠度wmax为
A
B 即选择A端固定B端自由的悬臂梁
L
FBy 作为基本静定梁。
MA
q
A
L
(2)解除A端阻止转动的支座反力
B
矩 M作A 为多余约束,即选择两端简
支的梁作为基本静定梁。
39
基本静定基选取可遵循的原则： (1) 基本静定基必须能维持静力平衡，且为几何不变 系统； (2) 基本静定基要便于计算，即要有利于建立变形协 调条件。一般来说，求解变形时，悬臂梁最为简单， 其次是简支梁，最后为外伸梁。
x3 6
C1x
C2
该梁的边界条件为：在 x=0 处 w 0，w =0
于是得
C1 0，C2 0
16
从而有 转角方程 q w Fxl Fx2
EI 2EI 挠曲线方程 w Fx2l Fx3
2EI 6EI
当x=L时：
qmax q
|xl
Fl 2 EI
Fl 2 2EI
Fl 2 2EI
静定梁(基本静定基) — 将超静定梁的多余约束解除，得到
相应的静定系统，该系统仅用静力平衡方程就可解出所有反力
以及内力。
多余约束 — 杆系在维持平衡的必要约束外所存在的多余约
束或多余杆件。
q
多余约束的数目=超静定次数
B 多余约束的数目=1