梁的刚度校核
梁的刚度计算

§10-6
RA
A
l 2
简 单 超 静 定 梁
RB
B
ql 2 mA 0, RBl 2 0. ql m 0 , R , RB 0.5ql. B A 2
q
C
l 2
静 定 问 题
由平衡方程可以解出全部未知数
RA
A
l 2
RC
C
ycq ycRC 0
A
C
B
多余反力 计算梁的内力、应力、强度、变形、刚度。
yB 0 RB
RA
A
l 2
RC
C
q
RB
B
l 2
例 已知梁的EI,梁的长度,求 各处的约束反力。
解:1) 受力分析,列平衡方程 判定超静定次数
q
A
RC
Y 0, RA RB RC ql 0 M A 0, RBl 0.5RCl 0.5ql2 0
I
=
A D
图1
B F1
图2
64
( D 4 d 4 ) 188 10 8 m 4
M
A L B
图3
+ +
F1 L2 F2 La 4 0 . 423 10 (弧度) B a 16EI 3EI C B F1L2 a F2 a 3 F2 a 2 L 6 y 5 . 19 10 m F 2 F2 C 2 16EI 3EI 3EI
3ql R A RB 16
RC l 3 5ql 4 0 384EI 48EI
RA
A
l 2
RC
C
东财在线建筑力学》第三套作业(第六~八单元)

C、强度条件要求杆内最大工作应力必须超过材料的许用应力
D、强度条件要求拉压杆件最大变形不超过正常工作的最大变形
答案:A
【2】在利用积分法计算梁位移时,待定的积分常数主要反映了( )。
A、剪力对梁变形的影响
B、对近似微分方程误差的修正
C、支承情况对梁变形的影响
D、梁截面形心轴向位移对梁变形的影响
【1】在纯剪切应力状态中,说法正确是( )。
A、主应力均为正值
B、最大主应力等于最大剪应力,最小主应力等于负的最大正应力
C、最大剪应力为零
D、最小主应力为零值
答案:B
【2】
图示 为 结 构 在 荷 载 作 用 下 的MP 图 , 各 杆 EI=常 数 ,支 座 B 截 面 处 的 转 角 为:
A、16/(EI)( 顺 时 针 )
【7】等截面直梁在弯曲变形时,挠曲线曲率在最大( )处一定最大。
A、挠度
B、转角
C、剪力
D、弯矩
答案:D
【8】
单元体的应力状态如图所示,由x轴至σ1方向的夹角为
A、13.5°
B、-76.5°
C、76.5°
D、13.5°
答案:D
【9】在单元体上,可以认为( )。
A、每个面上的应力是均匀分布的,一对平行面上的应力相等
答案:C
【3】
三种应力状态分别如图(a)、(b)、(c)所示,则三者间的关系为
A、完全等价
B、完全不等价
C、图(b)、图(c)等价
D、图(a)、图(c)等价
答案:D
【4】
已知应力圆如图所示,图(a)、(b)、(c)、(d)分别表示单元体的应力状态和A截面的应力,则与应力圆所对应的单元体为
孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-梁弯曲时的位移(圣才出品)

圣才电子书
ql3/6,D=-ql4/24。
十万种考研考证电子书、题库视频学习平台
故挠曲线方程和转角方程分别为:
w(x)=qx2(x2+6l2-4lx)/(24EI),θ(x)=q(x3-3lx2+3l2x)/(6EI)
则最大挠度 wmax=w(x)|x=l=ql4/(8EI);梁端转角 θB=θ(x)| x=l=ql3/(6EI)。
表 5-1-4 叠加原理计算梁的挠度和转角
四、梁的刚度校核·提高梁的刚度的措施(见表 5-1-5)
表 5-1-5 梁的刚度校核及提高措施
3 / 41
圣才电子书 十万种考研考证电子书、题库视频学习平台
五、梁内的弯曲应变能 定义:由于梁弯曲变形而存储的能量称为梁内的弯曲应变能。梁在弹性变形过程中,其 弯曲应变能与作用在梁上的外力所作的功相等,常见梁内的弯曲应变能见表 5-1-6。
则最大挠度 wmax=w(x)|x=l=Fl3/3EI;梁端转角 θB=θ(x)| x=l=Fl2/2EI。
图 5-2-1(a)(b) (2)建立如图 5-2-1(b)所示坐标系。 首先列弯矩方程:M(x)=-q(l-x)2/2,由此可得挠曲线近似方程: EIw″=-M(x)=q(l-x)2/2 积分得: EIw′=-q(l-x)3/6+C① EIw=q(l-x)4/24+Cx+D② 该梁的边界条件:x=0,w=0,x=0,w'=0。代入式①、②可确定积分常数:C=
圣才电子书
十万种考研考证电子书、题库视频学习平台
第 5 章 梁弯曲时的位移
5.1 复习笔记
梁在承受荷载时发生相应的变形,变形后轴线相对原位置将会发生位移、梁的截面将出 现转角,梁内会因变形存储能量。本章首先介绍梁的位移概念,并基于坐标系统建立挠曲线 方程;接着介绍求解梁的位移的方法,根据挠曲线近似微分方程积分和按叠加原理计算;再 介绍梁刚度校核以及提高梁刚度的方法;最后介绍梁弯曲应变能的概念及计算方法。
结构位移和刚度—梁的刚度计算(建筑力学)

二、用积分法求梁的变形
1.挠曲线近似微分方程
y( x)
M (x) EI
2.用积分法求变形 EI (x) M (x)dx C1
三、用叠加法求梁的变形
EIy(x) [ M (x)dx C1]dx C2
叠加法—梁截面的总变形,就等于各个荷载单独作用时产生变形的代数和。
四、梁的刚度计算 ymax [ f ]
梁的刚度计算
主要内容
梁的刚度条件和设计准则 梁的刚度计算 梁的刚度计算工程实例
梁的刚度计算
➢ 如果梁的弯曲变形过大,即使强度满足要求,也不能正常工作。例如:房 屋的楼面板或者梁长时间受较大荷载作用,导致变形过大,会造成抹灰面 出现裂缝,工业厂房的吊车梁变形过大,会影响吊车梁的正常使用等。设 计梁时,除了进行强度计算外,还应考虑进行刚度计算,需要把梁的最大 挠度和最大转角限制在一定的允许范围内。
l
l
课后作业:《建筑力学练习册》 练习二十五
3.6 4 4
3.6kN m
2、按正应力强度设计。查强度准则
3.6kNm
max
M max Wz
M max 0.1d 3
[ ]
得:
d3
M max
3
3.6 106 mm 153.3mm
0.1[ ] 0.110
取d=160mm
梁的刚度计算
3、按梁的刚度准则校核。
查变形表得
ymax
Fl 3 48EI
为:
ymax [ f ]
l
l
式中 ymax 为最大相对挠度,[ f ] 为许用相对挠度,其值可
l
l
根据梁的工作情况及要求查阅有关设计手册。土建工程中的许
用相对挠度值 [ f ] 常限制在
梁的变形与刚度计算
查表,得
y
C
y
4
Cq
y
Cm
l
q
A
2 5ql ml 384EI 16 EI
()
Bq
θA θAq θAm
3 ml ql 24 EI 3EI
Aq
m
A
C y cq
(
)
Bm
Am
C ycm
θB θBq θBm
3 ml ql 24 EI 6 EI
(
2
3
ml 16 EI
ml 3EI ml 3EI 一、梁的刚度条件
w
max
L
w L
max
1 1 w (对土建工程: ( ~ )) 250 1000 L
其中[]称为许用转角;[w/L]称为许用挠跨比。通常依此 条件进行如下三种刚度计算: 、校核刚度:
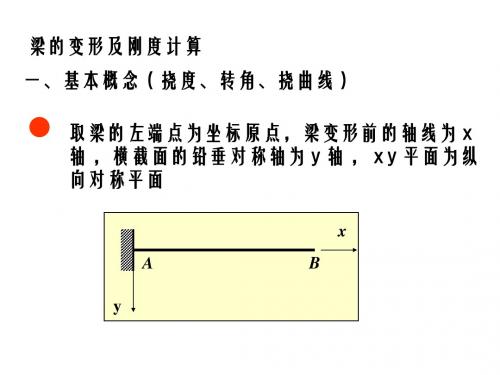
梁的变形及刚度计算 一、基本概念(挠度、转角、挠曲线) 取梁的左端点为坐标原点,梁变形前的轴线为 x 轴 ,横截面的铅垂对称轴为 y 轴 , x y 平面为纵 向对称平面
x
A
y
B
一、基本概念(挠度、转角、挠曲线)
度量梁变形后横截面位移的两个基本量 1、挠度( y): 横截面形心 C (即轴线上的点)在垂直于 x
例题求图示梁截面B的挠度
q A EIz
a C
B
L
解法1:为了利用附录IV表中的结果,可将原荷载视 为图(1)和图(2)两种情况的叠加
q A EIz
a C
B
L L c q (2) B
q A c L (1) B A
a
q
8.3.5 梁的刚度计算

8.3.5 梁的刚度计算梁的刚度计算,通常是校核其变形是否超过许用挠度[ f ]和许用转角[θ],可以表述为:≤y f []max≤θθ[]max式中y max 和θmax 为梁的最大挠度和最大转角。
在机械工程中,一般对梁的挠度和转角都进行校核;而在土木工程中,常常只校核挠度,并且以许用挠度与跨长的比值lf []作为校核的标准,即: ≤l lf y []max (8.17) 土木工程中的梁,强度一般起控制作用,通常是由强度条件选择梁的截面,再校核刚度。
例8.9 简支梁受力如图8.11所示,采用22a 号工字钢,其弹性模量=E 200GPa ,=l f 400[]1,试校核梁的刚度。
解:由附录查表可得=I 3400cm z 4,=EIy ql 3845max 4。
于是 =<=⨯⨯⨯⨯==⨯⨯l f l EI ql y 600400[]1138438420010MPa 340010mm 554N/mm 6000mm 344max 333所以梁的刚度满足要求。
下面介绍提高梁弯曲刚度的一些措施。
在不改变荷载的条件下,梁的变形与抗弯刚度EI 成反比,与跨长的n 次幂(n 可取1、2、3或4)成正比。
所以,提高弯曲刚度的一些措施有:(1)增大EI 。
这方面可以考虑采用惯性矩较大的工字形、槽形、箱形等截面形状。
须指出的是,高强钢与普通钢的弹性模量相差无几,所以采用高强钢对提高刚度的作用并不明显。
(2)调整跨长或改变结构。
减小跨长对变形的影响较为明显,如龙门吊车大梁就采用了两端外伸的结构形式。
此外,增加约束形成超静定梁,也能显著减小梁的变形,同时还可以提高弯曲强度。
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)。
东财在线建筑力学》第三套作业(第六

错误
答案:错误
【18】当梁发生平面弯曲变形时,梁的轴线仍然在纵向对称平面内。()
正确
错误
答案:正确
【19】梁的高度越大,则梁的抗弯能力也越大。()
正确
错误
答案:正确
【20】抗弯截面模量越大,则梁的抗弯曲能为越小。()
正确
错误
答案:错误
【1】关于拉压杆的强度条件,下列说法正确的是()。
A、为了保证拉压杆不致因强度不足而破坏
A、正方形
B、工字形
C、T形
D、矩形
E、圆形
答案:BCD
【12】为了提高梁的抗弯刚度,工程上常采用的截面形式有()。
A、正方形
B、工字形
C、T形
D、矩形
E、圆形
答案:BCD
【13】梁的正应力在横截面上是沿梁高呈线性分布且()。
A、中性轴上正应力为最大值
B、均匀分布
C、离中性轴最远的上下边缘正应力最大
A、13.5°
B、-76.5°
C、76.5°
D、13.5°
答案:D
【9】在单元体上,可以认为()。
A、每个面上的应力是均匀分布的,一对平行面上的应力相等
B、每个面上的应力是均匀分布的,一对平行面上的应力不等
C、每个面上的应力是非均匀分布的,一对平行面上的应力相等
D、每个面上的应力是非均匀分布的,一对平行面上的应力不等
B、提高杆件材料的强度能提高杆件的承载力
C、提高杆件材料的强度能提高杆件的刚度
D、提高杆件材料的刚度能提高压杆的稳定性
E、提高杆件材料的刚度能提高杆件的承载力
答案:BD
【13】两截面不同,材料相同的拉杆,受到相同的轴力作用时则其()。
大梁的简单校核计算

大梁的简单校核计算大梁是建筑结构中常见的承重构件,用于支撑和传递楼板和屋面的荷载至柱子或墙体上。
在设计和施工大梁时,需要进行校核计算,以确保其安全可靠。
下面是一个对大梁进行简单校核计算的步骤和方法。
首先,需要确定大梁的截面形状和尺寸。
常见的大梁形状包括矩形、T形、I形等,尺寸一般由设计要求决定。
根据大梁的截面形状和尺寸,可以计算得到其截面面积和截面惯性矩。
接下来,需要确定大梁所承受的荷载。
荷载包括常规荷载和临时荷载,常规荷载来自楼板、屋面和人员活动等,临时荷载来自施工期间的施工载荷。
根据设计规范和实际情况,可以确定大梁所承受的设计荷载。
然后,需要进行弯曲和剪切校验。
对于弯曲校验,需要根据大梁的截面形状和荷载,计算得到大梁所受的弯曲应力,然后与材料的弯曲极限强度进行比较,确保大梁在弯曲方面的安全性。
对于剪切校验,需要根据大梁的截面形状和荷载,计算得到大梁所受的剪切应力,然后与材料的剪切强度进行比较,确保大梁在剪切方面的安全性。
最后,需要进行挠度校验。
大梁的挠度是指其在荷载作用下产生的弯曲变形。
需要根据大梁的杆件刚度和荷载计算得到大梁的挠度,然后与设计要求进行比较,确保大梁的挠度在允许范围内。
此外,还需要对连接部位进行校核计算。
大梁与柱子或墙体之间的连接处需要确保连接刚度和承载能力。
计算连接部位的强度和稳定性,以确保连接处的安全性。
在进行大梁的简单校核计算时,需要参考相关的设计规范和标准。
常用的设计规范包括《建筑结构荷载规范》、《建筑抗震设计规范》等。
根据不同的设计要求和实际情况,还可以考虑使用计算软件进行校核和分析。
总之,大梁的简单校核计算是设计和施工中必不可少的一步,通过对大梁的截面形状、荷载以及弯曲、剪切和挠度等进行计算和分析,可以确保大梁的安全可靠性,同时保证建筑结构的整体稳定性和承载能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
II、 II、 提高梁的刚度的措施
梁的位移(挠度和转角) 梁的位移(挠度和转角)除了与梁的支承和荷载情况有 关外,还取决于以下三个因素: 关外,还取决于以下三个因素: 成正比; 材料 —— 梁的位移与材料的弹性模量 E成正比; 成正比 截面 ——梁的位移与截面的惯性矩 I 成正比; 梁的位移与截面的惯性矩 成正比; 跨长 ——梁的位移与跨长 梁的位移与跨长 次幂成正比 成正比。 的 n 次幂成正比。
为了减小梁的位移, 为了减小梁的位移,可采取下列措施 增大梁的抗弯刚度EI 增大梁的抗弯刚度 工程中常采用工字形, 工程中常采用工字形 箱形截面
梁的刚度条件及提高梁刚度的措施
提高梁刚度的措施 1)选择合理的截面形状
调整跨长和改变结构 设法缩短梁的跨长,将能显著地减小其挠度和转角。 设法缩短梁的跨长,将能显著地减小其挠度和转角。这 是提高梁的刚度的一个很又效的措施。 是提高梁的刚度的一个很又效的措施。
(a) q
桥式起重机的钢梁通常采 用两端外伸的结构(图 用两端外伸的结构( 6 -6 a),就是为了缩短 ),就是为了缩短 ), 跨长而减小梁的最大挠度 值。 图 6 -6
(b) q A B A B
q
同时,由于梁的外伸部分的自重作用, 同时,由于梁的外伸部分的自重作用,将使两的 AB 跨产 生向上的挠度(图6 -6 b),从而使AB跨向下的挠度能够 生向上的挠度( ),从而使 跨向下的挠度能够 ),从而使 被抵消一部分,而有所减小。 被抵消一部分,而有所减小。
(a) q
增加梁的支座也可以减小梁 的挠度。 的挠度。
(b) q A B A B
q
图 6 -6
梁的刚度条件及提高梁刚度的措施
改善结构形式, 改善结构形式,减少弯矩数值
改 变 支 座 形 式
梁的刚度条件及提高梁刚度的措施
2)改善结构形式,减少弯矩数值 改善结构形式,改 变 载 Nhomakorabea荷 类 型
wC2 = 62.5% wC1
f 1 [ ]= l 400
120KN 30KN C 40KN 12KN B
A
fC
0.4 0.4 0.7 2.4 m 0.3 0.6
例题 6 -7 图
解:可将梁跨中点C处的挠度 fC作为梁的最大挠度 fmax 。 可将梁跨中点 处的挠度
f max ≈ f C =
4 i =1
∑
Pi bi [ 3l 2 4bi2 ] = 4.67 mm 48 EI
40KN 12KN C B
120KN 30KN
A
fC
0.4 0.4 0.7 2.4 m 0.3 0.6
梁的许可挠度为
3 f 1 [ f ] = [ ]×l = m × 2.4 = 6×10 m = 6m l 400
f max = 4.67mm < [ f ]
因此, 所选用的槽钢能够满足刚度条件的要求。 因此, 所选用的槽钢能够满足刚度条件的要求。
梁的刚度条件及提高梁刚度的措施
采用超静定结构
§7-5 梁的刚度条件及提高梁刚度的措施
采用超静定结构
§6-4
梁的刚度校核 提高梁的刚度的措施 I、 梁的刚度校核 、
对于梁的挠度, 其许可值通常用许可的挠度与梁跨长的比值 对于梁的挠度
f [ ] 作为标准。 梁的刚度条件可表示为 作为标准。 l
fm f ax ≤[ ] l l
(6 -5) )
θ θm ≤ [ ] ax
的简支梁, 例题 6-7 试按刚度条件校核第五章例题 5-10 的简支梁 已知 号槽钢, 按强度条件所选择的梁为两根 20a 号槽钢 每根槽钢的惯性矩 I=1780cm , 钢的弹性模量为 E=210GPa 。 此梁的许可挠度与梁 跨长的比值为
