第章时间序列分析课后习题答案
计量经济学精要习题参考答案(第四版)

计量经济学(第四版)习题参考答案第一章 绪论1.1 一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析1.2 我们在计量经济模型中列出了影响因变量的解释变量,但它(它们)仅是影响因变量的主要因素,还有很多对因变量有影响的因素,它们相对而言不那么重要,因而未被包括在模型中。
为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4 估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y 就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2 NS S x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
2.3 原假设 120:0=μH备择假设 120:1≠μH 检验统计量()10/25XX μσ-Z ====查表96.1025.0=Z 因为Z= 5 >96.1025.0=Z ,故拒绝原假设, 即此样本不是取自一个均值为120元、标准差为10元的正态总体。
2012版金融计量学课后习题答案

⇒ yt = (1 − θ1 ) −1 c − (θ1 − α 1 ) yt −1 − θ1 (θ1 − α1 ) yt − 2 − θ1 (θ1 − α1 ) yt −3 + …… + ε t
2
(3) 结论变为
yt = (1 − α1 ) −1 c + ε t yt = (1 − θ1 ) −1 c + ε t
+…+
∂yt + j ∂ε t + j
= α j −1 (αb1 + b2 ) + α j −2 (αb1 + b2 ) + … + (αb1 + b2 ) + b1 = b1 ∑ α i + b2 ∑ α i
i =0 i =0 j −1
3、 解方程得,λ1 = 1 ,λ2 = 0.2. 有一个单位根, (1) 特征方程:λ2 − 1.2λ + 0.2 = 0 , 是非平稳的。 逆特征方程:1 − 1.2 z + 0.2 z 2 = 0 ,解方程得, z1 = 1 ,z 2 = 5.(互为倒数) , ( 2 ) 特 征 方 程 : λ 2 − 1 .2 λ + 0 .4 = 0 , 解 方 程 , 无 实 数 解 , 复 数 解 为
2
(2)
(1 − α 1 L) yt = c + (1 − θ1 L)ε t 两边同时乘以(1 − θ1 L) −1,得 (1 − α 1 L)(1 − θ1 ) −1 yt = (1 − θ1 ) −1 c + ε t ⇒ (1 − α 1 L)(1 + θ1 L + θ1 L2 + ……) yt = (1 − θ1 ) −1 c + ε t
统计学课后答案(第3版)第10章时间序列分析习题答案
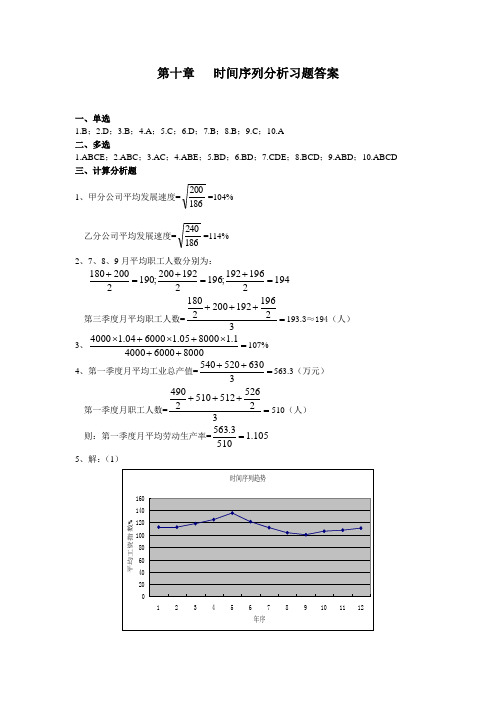
第十章 时间序列分析习题答案一、单选1.B ;2.D ;3.B ;4.A ;5.C ;6.D ;7.B ;8.B ;9.C ;10.A 二、多选1.ABCE ;2.ABC ;3.AC ;4.ABE ;5.BD ;6.BD ;7.CDE ;8.BCD ;9.ABD ;10.ABCD 三、计算分析题1、甲分公司平均发展速度=186200=104% 乙分公司平均发展速度=186240=114% 2、7、8、9月平均职工人数分别为:1942196192;1962192200;1902200180=+=+=+ 第三季度月平均职工人数==+++321961922002180193.3≈194(人) 3、=++⨯+⨯+⨯8000600040001.1800005.1600004.14000107%4、第一季度月平均工业总产值==++3630520540563.3(万元)第一季度月职工人数==+++325265125102490510(人) 则:第一季度月平均劳动生产率=105.15103.563=5、解:(1)(2)年序t 平均工资指数(环比)5期移动平均趋势1 112.70% —2 112.60% —3 118.50% 120.80%4 124.80% 122.60%5 135.40% 122.50%6 121.70% 119.52%7 112.10% 114.60%8 103.60% 108.76%9 100.20% 106.00%10 106.20% 105.78%11 107.90% —12 111.00% —各年份移动平均趋势值和原序列如下:移动平均可以消除原序列中的一些随机扰动和短期波动,期数越长,平滑作用越强;移动平均的作用就是消除序列随机和短期影响,从而能够发现序列的趋势。
(3)年份平均工资指数(环比)指数平滑值α=0.3误差平方指数平滑值α=0.5误差平方1 112.70% ————2 112.60% 112.70% 1E-06 112.70% 1E-063 118.50% 112.67% 0.003399 112.65% 0.0034224 124.80% 114.42% 0.010777 115.58% 0.008515 135.40% 117.53% 0.031922 120.19% 0.0231426 121.70% 122.89% 0.000142 127.79% 0.0037137 112.10% 122.54% 0.01089 124.75% 0.0159948 103.60% 119.40% 0.024979 118.42% 0.0219739 100.20% 114.66% 0.020919 111.01% 0.01168910 106.20% 110.32% 0.001701 105.61% 3.53E-0511 107.90% 109.09% 0.000141 105.90% 0.00039912 111.00% 108.73% 0.000515 106.90% 0.00168—109.41% —108.95% —合计 — — 0.105385 — 0.09056从上表数据看,采用平滑系数α=0.5拟合效果好。
应用时间序列分析课后习题答案
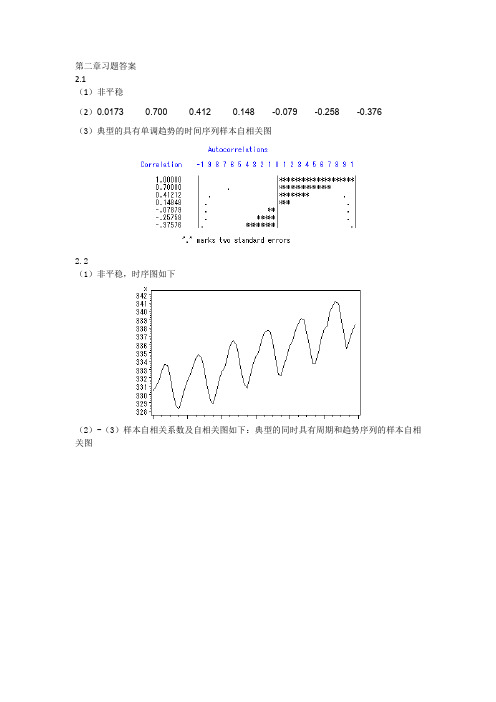
第二章习题答案2.1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图2.3(1)自相关系数为:0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118(2)平稳序列(3)白噪声序列2.4,序列LB=4.83,LB统计量对应的分位点为0.9634,P值为0.0363。
显著性水平=0.05不能视为纯随机序列。
2.5(1)时序图与样本自相关图如下(2) 非平稳 (3)非纯随机 2.6(1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机第三章习题答案3.1 解:1()0.7()()t t t E x E x E ε-=⋅+0)()7.01(=-t x E 0)(=t x E t t x ε=-)B 7.01(t t t B B B x εε)7.07.01()7.01(221Λ+++=-=- 229608.149.011)(εεσσ=-=t x Var49.00212==ρφρ 022=φ3.2 解:对于AR (2)模型:⎩⎨⎧=+=+==+=+=-3.05.02110211212112011φρφρφρφρρφφρφρφρ 解得:⎩⎨⎧==15/115/721φφ3.3 解:根据该AR(2)模型的形式,易得:0)(=t x E原模型可变为:t t t t x x x ε+-=--2115.08.02212122)1)(1)(1(1)(σφφφφφφ-+--+-=t x Var2)15.08.01)(15.08.01)(15.01()15.01(σ+++--+==1.98232σ⎪⎩⎪⎨⎧=+==+==-=2209.04066.06957.0)1/(1221302112211ρφρφρρφρφρφφρ ⎪⎩⎪⎨⎧=-====015.06957.033222111φφφρφ 3.4 解:原模型可变形为:t t x cB B ε=--)1(2由其平稳域判别条件知:当1||2<φ,112<+φφ且112<-φφ时,模型平稳。
统计学习题答案 第9章 时间序列分析

第9章 时间序列分析——练习题●1. 某汽车制造厂2003年产量为30万辆。
(1)若规定2004—2006年年递增率不低于6%,其后年递增率不低于5%,2008年该厂汽车产量将达到多少?(2)若规定2013年汽车产量在2003年的基础上翻一番,而2004年的增长速度可望达到7.8%,问以后9年应以怎样的速度增长才能达到预定目标?(3)若规定2013年汽车产量在2003年的基础上翻一番,并要求每年保持7.4%的增长速度,问能提前多少时间达到预定目标?解:设i 年的环比发展水平为x i ,则由已知得:x 2003=30, (1)又知:320042005200620032004200516%x x x x x x ≥+(),2200720082006200715%x x x x ≥+(),求x 2008由上得32200820072008200320032007(16%)(15%)x x x x x x =≥++ 即为3220081.061.0530x ≥,从而2008年该厂汽车产量将达到 得 x 2008≥30× 31.06×21.05= 30×1.3131 = 39.393(万辆) 从而按假定计算,2008年该厂汽车产量将达到39.393万辆以上。
(2)规定201320032x x =,20042003x x =1+7.8%由上得=107.11%==可知,2004年以后9年应以7.11%的速度增长,才能达到2013年汽车产量在2003年的基础上翻一番的目标。
(3)设:按每年7.4%的增长速度n 年可翻一番, 则有 201320031.0742na a == 所以 1.074log 20.30103log 29.70939log1.0740.031004n ====(年)可知,按每年保持7.4%的增长速度,约9.71年汽车产量可达到在2003年基础上翻一番的预定目标。
原规定翻一番的时间从2003年到2013年为10年,故按每年保持7.4%的增长速度,能提前0.29年即3个月另14天达到翻一番的预定目标。
时间序列分析课后习题答案1

时间序列分析课后习题答案(上机第二章 2、328330332334336338340342(1时序图如上:序列具有明显的趋势和周期性,该序列非平稳。
(2样本自相关系数:(3该样本自相关图上,自相关系数衰减为 0的速度缓慢,且有正弦波状,显示序列具有趋势和周期,非平稳。
3、 (1样本自相关系数:(2序列平稳。
(3因 Q 统计量对应的概率均大于 0.05,故接受该序列为白噪声的假设,即序列为村随机序列。
5、 (1时序图和样本自相关图:50100150200250300350(2序列具有明显的周期性,非平稳。
(3序列的 Q 统计量对应的概率均小于 0.05,该序列是非白噪声的。
6、 (1根据样本相关图可知:该序列是非平稳,非白噪声的。
(2对该序列进行差分运算:1--=t t t x x y {t y }的样本相关图:该序列平稳,非白噪声。
第三章:17、 (1结论:序列平稳,非白噪声。
(2 拟合 MA(2 model:VariableCoefficient Std. Error t-Statistic Prob. C 80.40568 4.630308 17.36508 0.0000 MA(1 0.336783 0.114610 2.938519 0.0047 R-squared0.171979 Mean dependent var 80.29524 Adjusted R-squared 0.144379 S.D. dependent var 23.71981 S.E. of regression 21.94078 Akaike info criterion 9.061019 Sum squared resid 28883.87 Schwarz criterion 9.163073 Log likelihood -282.4221 F-statistic 6.230976 Durbin-Watson stat 2.072640 Prob(F-statistic 0.003477Residual tests(3拟合 AR(2model:C 79.71956 5.442613 14.64729 0.0000 AR(10.2586240.1288102.0077940.0493R-squared0.154672 Mean dependent var 79.50492 Adjusted R-squared 0.125522 S.D. dependent var 23.35053 S.E. of regression 21.83590 Akaike info criterion 9.052918 Sum squared resid 27654.79 Schwarz criterion 9.156731 Log likelihood -273.1140 F-statistic 5.306195 Durbin-Watson stat 1.939572 Prob(F-statistic 0.007651Inverted AR Roots.62-.36Residual tests:(4 拟合 ARMA (2, 1 model :Variable Coefficient Std. Error t-Statistic Prob. C 79.17503 4.082908 19.39183 0.0000 AR(1 -0.586834 0.118000 -4.973170 0.0000 AR(2 0.376120 0.082091 4.581756 0.0000 MA(11.1139990.09712211.470120.0000R-squared0.338419 Mean dependent var 79.50492 Adjusted R-squared 0.303599 S.D. dependent var 23.35053 S.E. of regression 19.48617 Akaike info criterion 8.840611 Sum squared resid 21643.51 Schwarz criterion 8.979029 Log likelihood-265.6386 F-statistic9.719104Inverted AR Roots .39-.97 Inverted MA Roots-1.11Estimated MA process is noninvertible残差检验:(5拟合 ARMA (1, (2 model:Variable Coefficient Std. Error t-Statistic Prob. C 79.52100 4.621910 17.205230.0000 AR(1 0.270506 0.125606 2.153603 0.0354 R-squared0.157273 Mean dependent var 79.55161 Adjusted R-squared 0.128706 S.D. dependent var 23.16126 S.E. of regression 21.61946 Akaike info criterion 9.032242 Sum squared resid 27576.65 Schwarz criterion 9.135167 Log likelihood -276.9995 F-statistic 5.505386 Durbin-Watson stat 1.981887 Prob(F-statistic 0.006423Inverted AR Roots.27残差检验:(6优化根据 SC 准则,最优模型为 ARMA(2,1模型。
第章时间序列预测习题答案完整版

第章时间序列预测习题答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】第10章时间序列预测从时间序列图可以看出,国家财政用于农业的支出额大体上呈指数上升趋势。
(2)年平均增长率为:。
(3)。
下表是1981年—2000年我国油彩油菜籽单位面积产量数据(单位:kg / hm2)年份单位面积产量年份单位面积产量1981 1451 1991 12151982 1372 1992 12811983 1168 1993 13091984 1232 1994 12961985 1245 1995 14161986 1200 1996 13671987 1260 1997 14791988 1020 1998 12721989 1095 1999 14691990 1260 2000 1519(1)绘制时间序列图描述其形态。
(2)用5期移动平均法预测2001年的单位面积产量。
(3)采用指数平滑法,分别用平滑系数a=和a=预测2001年的单位面积产量,分析预测误差,明用哪一个平滑系数预测更合适?详细答案:(1)时间序列图如下:(2)2001年的预测值为:|(3)由Excel输出的指数平滑预测值如下表:年份单位面积产量指数平滑预测a=误差平方指数平滑预测a=误差平方19811451 19821372 19831168 19841232 19851245 19861200 1987126019881020198910951990126019911215199212811993130919941296199514161996136719971479199812721999146920001519合计———2001年a=时的预测值为:a=时的预测值为:比较误差平方可知,a=更合适。
下面是一家旅馆过去18个月的营业额数据月份营业额(万元)月份营业额(万元)1 295 10 4732 283 11 4703 322 12 4814 355 13 4495 286 14 5446 379 15 6017 381 16 5878 431 17 6449 424 18 660(1)用3期移动平均法预测第19个月的营业额。
(完整word版)时间序列分析基于R__习题答案及解析
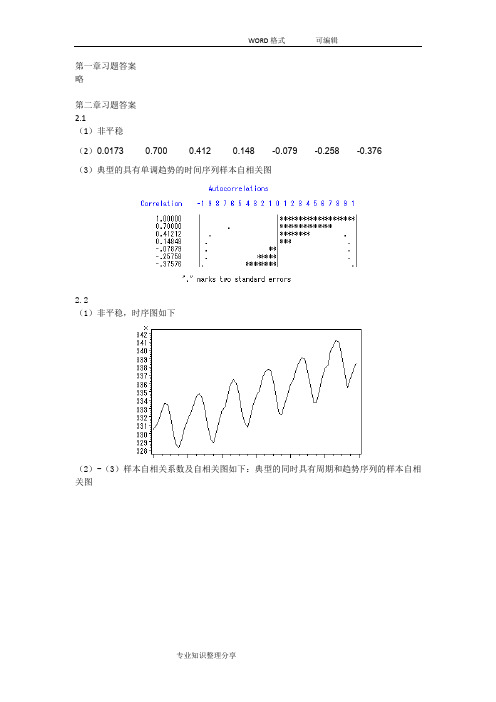
第一章习题答案略第二章习题答案2.1(1)非平稳(2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376(3)典型的具有单调趋势的时间序列样本自相关图2.2(1)非平稳,时序图如下(2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图2.3(1)自相关系数为:0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118(2)平稳序列(3)白噪声序列2.4,序列LB=4.83,LB统计量对应的分位点为0.9634,P值为0.0363。
显著性水平=0.05不能视为纯随机序列。
2.5(1)时序图与样本自相关图如下(2) 非平稳 (3)非纯随机 2.6(1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机第三章习题答案3.1 ()0t E x =,21() 1.9610.7t Var x ==-,220.70.49ρ==,220φ= 3.2 1715φ=,2115φ=3.3 ()0t E x =,10.15() 1.98(10.15)(10.80.15)(10.80.15)t Var x +==--+++10.80.7010.15ρ==+,210.80.150.41ρρ=-=,3210.80.150.22ρρρ=-=1110.70φρ==,2220.15φφ==-,330φ=3.4 10c -<<, 1121,1,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩3.5 证明:该序列的特征方程为:32--c 0c λλλ+=,解该特征方程得三个特征根:11λ=,2c λ=3c λ=-无论c 取什么值,该方程都有一个特征根在单位圆上,所以该序列一定是非平稳序列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第9章 时间序列分析课后习题答案
第10章
(1)30× 3
1.06×2
1.05= 30×1.3131 = 39.393(万辆)
(2117.11%== (3)设按7.4%的增长速度n 年可翻一番
则有 1.07460/30n
==
所以 n = log2 / log1.074 = 9.71(年)
故能提前0.29年达到翻一番的预定目标。
第11章
(1)以1987年为基期,2003年与1987年相比该地区社会商品零售额共增长:
%86.2313186.213186.31%)8.61(%)2.81(%)101(5
5
5
==-=-+⨯+⨯+
(2)年平均增长速度为
1%)8.61(%)2.81(%)101(15
555-+⨯+⨯+=0.0833=8.33%
(3) 2004年的社会商品零售额应为
509.52)0833.01(307=+⨯(亿元)
第12章 (1)发展总速度%12.259%)81(%)101(%)121(3
43=+⨯+⨯+
平均增长速度=
%9892.91%12.25910=-
(2)8.561%)61(5002
=+⨯(亿元)
(3)平均数∑====415
.1424570
41j j y y (亿元),
2002
年一季度
的计划
任务
:
625.1495.142%105=⨯(亿元)。
第13章
(1)用每股收益与年份序号回归得
^
0.3650.193t Y t =+。
预测下一年(第11年)的每股收益
为488.211193.0365.0ˆ
11=⨯+=Y 元
(2)时间数列数据表明该公司股票收益逐年增加,趋势方程也表明平均每年增长0.193元。
是一个较为适合的投资方向。
第14章 (1)移动平均法消除季节变动计算表
(2)t T t ⨯+=63995.09625.8
上表中,其趋势拟合为直线方程t T t ⨯+=63995.09625.8。
根据上表计算的季节比率,按照公式KL t t t S T Y -⋅=计算可得: 2004年第一季度预测值:
7723.21097301.1)1763995.09625.8(ˆˆˆ11717=⨯⨯+=⋅=S T Y
2004年第二季度预测值: 49725.23147237.1)1863995.09625.8(ˆˆˆ21818=⨯⨯+=⋅=S T Y
2004年第三季度预测值: 009.18852641.0)1963995.09625.8(ˆˆˆ31919=⨯⨯+=⋅=S T Y
2004年第四季度预测值:
6468.19902822.0)2063995.09625.8(ˆˆˆ42020=⨯⨯+=⋅=S T Y
平均法计算季节比率表:
季节比率的图形如下:
(2)用移动平均法分析其长期趋势
原时间序列与移动平均的趋势如下图所示:
9.2(1)采用线性趋势方程法:
t
T
i
0065
.7
0607
.
460
ˆ+
=剔除其长期趋势。
剔除长期趋势后分析其季节变动情况表
(3)运用分解法可得到循环因素如下图:。
