单一参数的交流电路
合集下载
单一参数正弦交流电路分析
? 平均功率或有功功率 P=0
iut+-p
,
? 无功功率 QC
iQ
C
用无功功率 QC衡量电容元件与外界交换能量的规模，即
无功功率计算式
QC
?
?UI
?
?I 2 XC
?
?
U2 XC
无功功率单位 乏尔（Var）
交换能量过程分析 p ? ui ? ?U Isin2? t
i
u
ωt
i
i
u
u
i
i
u
u
p 放电 P > 0 放电
教学内容 电阻R、电感 L、电容 C元件的电压电流关系，相 量形式的基尔霍夫定律（ KVL、KCL）。
教学要求 1.掌握单一元件的电压电流关系。 2.熟练应用相量形式的 KVL、KCL进行电路分
析。 教学重点和难点
重点： 单一元件的电压电流关系和相量形式的 基尔霍夫定律应用。
难点： 电阻 R、电感 L、电容 C元件电压电流关 系的分析。
【讨论】 指出下列各式中哪些是对的，哪些是错的？
在电阻电路中： 在电感电路中：
在电容电路中：
I?U R
i? U R
i? u R
I? ? U? R
i? u XL
U ? jωL I
I? U ωL
U? I?
?
jX L
U? I?
?
XL u
?
L di dt
i? u ωL
U ? I ?ω C
u ? i ?X C
三、纯电容电路
1.电容元件
定义电容为 C ? q
u
根据电流 i ? dq dt
i ? C duc dt
8.1 单一参数的交流电路
8.1 单一参数的交流电路考纲要求：1、熟练掌握纯电阻电路、纯电感电路和纯电容电路中电流和电压的关系及功率。
2、理解电阻、电感和电容在直流电路和交流电路中的作用。
3、理解正弦交流电路中感抗、容抗、有功功率、无功功率、视在功率、功率因数、阻抗、复数阻抗、电压三角形、电流三角形、阻抗三角形、功率三角形的概念。
教学目的要求：1、掌握单一参数电路中电压与电流的大小关系、相位关系和功率关系2、掌握单一参数的复数形式教学重点：掌握单一参数电路中电压与电流的大小关系、相位关系和功率关系教学难点：单一参数电路的复数形式课时安排：3节 课型：复习教学过程：【知识点回顾】一、纯电阻电路1、定义： 。
2、纯电阻电路中电压与电流的关系（1）大小关系：I= （2）相位关系：电压与电流 电压与电流的波形图和相量图：（3）纯电阻电路的复阻抗Z R =∙∙I U R =3、纯电阻电路中的功率（1）有功功率： 电阻消耗的功率P=（2）无功功率： （3）视在功率：二、纯电感电路1、定义： 。
2、纯电感电路中，电感对交流电的阻碍作用来源：感抗： 即X L = = （Ω）2、纯电感电路中电压与电流的关系（1）大小关系：I= （2）相位关系： 超前 900 电压与电流的波形图和相量图（3）纯电感电路的复阻抗Z L =∙∙I U L = 3、纯电感电路中的功率（1）有功功率： P= = （2）无功功率： Q= =（3）视在功率：S= =三、纯电容电路1、定义： 。
2、纯电容电路中，电容对交流电的阻碍作用来源： 。
容抗： 。
即X C = = （Ω）2、纯电容电路中电压与电流的关系（1）大小关系：I= （2）相位关系： 超前 900 电压与电流的波形图和相量图（3）纯电容电路的复阻抗Z L =∙∙I U C =3、纯电容电路中的功率（1）有功功率： P= = （2）无功功率： Q= =（3）视在功率： S= =【课前练习】一、判断题：1、在纯电阻电路中电阻值与频率反正比。
3.3单一参数的交流电路
X = R + X arctan = Z φ R
2 2
-
-
分压公式：
+
I
Z
Z1 U U1 Z1 Z 2
U2
Z2 U Z1 Z 2
U -
例:
有两个阻抗 Z1 6.16 j9Ω、 Z 2 2.5 - j4Ω
它们串联接在 U 22030V 的电源上， 求 I 和 U1 、U 2 并作相量图。
解： Z Z1 Z 2 (6.16 2.5) j (9 - 4)
8.66 j 5 1030 ()
I
I
+
U
+ Z1 U 1
U 220 30 Z 1030
220
+ Z2 U 2
-
U1 Z1 I (6.16 j 9) 22V 239.855.6V
1 1 1
3.相量电路模型
例：若有－4j，则知XC=4Ω
例1. 一电感线圈，L=100mH，f=50HZ (1) i 7 2 sint A , 求 u=? (2) U=127∠-30°V， 求I并画相量图。 解(1) ： XL=2πf L =31.4 (Ω) U=7×31.4 =220 (V) ∴ u= 220 2 sin( t 90º )V 解(2) ： 已知U=127 V ∴ I=U/XL= 4 (A)， -90° I= 4 -30° IL
不一定！
三、 阻抗的并联
Z1 Z 2 Z Z1 Z 2 Z1 Z 2
分流公式：
I
+
U
Z1
Z2
-
2 2
-
-
分压公式：
+
I
Z
Z1 U U1 Z1 Z 2
U2
Z2 U Z1 Z 2
U -
例:
有两个阻抗 Z1 6.16 j9Ω、 Z 2 2.5 - j4Ω
它们串联接在 U 22030V 的电源上， 求 I 和 U1 、U 2 并作相量图。
解： Z Z1 Z 2 (6.16 2.5) j (9 - 4)
8.66 j 5 1030 ()
I
I
+
U
+ Z1 U 1
U 220 30 Z 1030
220
+ Z2 U 2
-
U1 Z1 I (6.16 j 9) 22V 239.855.6V
1 1 1
3.相量电路模型
例：若有－4j，则知XC=4Ω
例1. 一电感线圈，L=100mH，f=50HZ (1) i 7 2 sint A , 求 u=? (2) U=127∠-30°V， 求I并画相量图。 解(1) ： XL=2πf L =31.4 (Ω) U=7×31.4 =220 (V) ∴ u= 220 2 sin( t 90º )V 解(2) ： 已知U=127 V ∴ I=U/XL= 4 (A)， -90° I= 4 -30° IL
不一定！
三、 阻抗的并联
Z1 Z 2 Z Z1 Z 2 Z1 Z 2
分流公式：
I
+
U
Z1
Z2
-
电工学第3章交流电路2
U Z = I
+ i R L C − + − + uR uL
u
− + u − C
ϕ = ψ u −ψ i
结论： Ｚ 的模为电路总电压和总电流有效值之比， Ｚ 的幅角则为总电压和总电流的相位差。
3.4 串联交流电路
U = UR + UL + UC =[R + j ( XL－XC )]I U =ZI
3. 相量图
UL U C
由相量图可求得
U UX X UR 0＜ ϕ ＜ 90° 感性电路 I
│Z│
U = U R + (U L − U C )
2
2
2 2
ϕ
R UC
= I R + ( X L − XC ) =I R +X
2 2
R = Z cos ϕ X = Z sin ϕ
由阻抗三角形得
=I Z
Z = R 2 + ( X L − X C )2 X L − XC R
= Z e jϕ = Z ∠ϕ
− + u − C
阻抗 三角形
R2 + X2
阻抗模:│Z│=√
阻抗角: ϕ = arctan (X / R)
ϕ
|Z|
X
3.4 串联交流电路
U = UR + UL + UC =[R + j ( XL－XC )]I U =ZI 2. 阻抗 Z 由 U =Z I 可得： U = U∠ψ u = U ∠ψ −ψ = Z ∠ϕ Z= u i I∠ ψ i I I
二、纯电容电路
1. 电压、电流的关系
设 由 有 式中 容抗
i + u – C
+ i R L C − + − + uR uL
u
− + u − C
ϕ = ψ u −ψ i
结论： Ｚ 的模为电路总电压和总电流有效值之比， Ｚ 的幅角则为总电压和总电流的相位差。
3.4 串联交流电路
U = UR + UL + UC =[R + j ( XL－XC )]I U =ZI
3. 相量图
UL U C
由相量图可求得
U UX X UR 0＜ ϕ ＜ 90° 感性电路 I
│Z│
U = U R + (U L − U C )
2
2
2 2
ϕ
R UC
= I R + ( X L − XC ) =I R +X
2 2
R = Z cos ϕ X = Z sin ϕ
由阻抗三角形得
=I Z
Z = R 2 + ( X L − X C )2 X L − XC R
= Z e jϕ = Z ∠ϕ
− + u − C
阻抗 三角形
R2 + X2
阻抗模:│Z│=√
阻抗角: ϕ = arctan (X / R)
ϕ
|Z|
X
3.4 串联交流电路
U = UR + UL + UC =[R + j ( XL－XC )]I U =ZI 2. 阻抗 Z 由 U =Z I 可得： U = U∠ψ u = U ∠ψ −ψ = Z ∠ϕ Z= u i I∠ ψ i I I
二、纯电容电路
1. 电压、电流的关系
设 由 有 式中 容抗
i + u – C
单相正弦交流电路—单一参数元件的电路
幅角:
i 90o
二、 C元件电路的功率
1. 瞬时功率 p
i
u
i
u
C
2 I sin t
2U sin( t 90 )
p i u U I sin 2 t
在关联参考方向下，功率有时大于零，有时小于零，电容元件在电路中的作
用是怎样的呢？
p i u iU I sin2ut
o
U I R
三、 R元件电路的功率
1. 瞬时功率 p：瞬时电压与瞬时电流的乘积
i
u
i I m sin ( t )
u U m sin ( t )
R
U m Im
p u i U m I m sin t
(1 cos 2t )
2
UI (1 cos 2t ) UI UI sin(2t 900 )
U IL
3. 有效值
电压、电流波
形图
u
i
90
定义：
t
X L L 2 fL
则：
U I XL
感抗（Ω）
关于感抗的讨论
感抗（ XL ωL 2πfL）是频率的函数，频率越高,感抗越大,频率越低,感抗越
小。电感有通低频，阻高频的特性。
UL I X L
R
+
_
f=0时
e
L
0.45 / 60o ( A)
R
484
i 0.45 2 sin(314t 60o )( A)
P UI 220 0.45 100(W )
在关联参考方向下，功率有时大于零，有时小于零，电感元件在电路中的作
用是怎样的呢？
单一参数的交流电路
R
•
I
波
Im
向 量 图
0
I• U•
Re
形 图
0
t
i
i
i = Imsin t +
u = Umsin t u
R
–
i、u、p
瞬时功率：电路在某一瞬间吸收 或放出的功率
u
p = u i =UI(1– cos2 t )
i
平均功率：瞬时功率在一周内的平均值 0
P = I U = I2 R
转换成的热能 W= P t
平均功率 P =0
i
无功功率 Q =UI=XC I2 =
U2 XC
波形图
u
电容与电源之间能量交换的规模
0
t
称为无功功率。其值为瞬时功
率的最大值，单位为(Var) 乏。
p
+
+
电容不消耗功率，它是储能元件。 0
–
– t
解：由线圈两端电压的解析式 u 100 2 sin 314tV可以得到
U=100V， 314rad / s, 0,
•
U 1000V
线圈的感抗为
X L L 314 0.01 3.14
•
•
I
U
100 0
31.85(90) A
jX L 190 3.14
因此通过线圈的电流瞬时值表达式为
i 31.85 2 sin(314t 90) A
i = Imsin( t + 90)
i u
波 形 图0
Im
• I
• U
t 0
Re
相量图
电流超前电压 90
电压与电流大小关系 U = I XC
2.2单一参数正弦交流电路
(2.27)
2.2 单一参数的正弦交流电路
2.功率关系 (1)瞬时功率
(2.28)
电感电路中，瞬时功率是一个最大值是 ，并以2ω的 角频率随时间而变化的交变量，其波形如图2.11（d） 所示。
2.2 单一参数的正弦交流电路
(2)平均功率
(2.29)
从图2.11（d）的波形图也可看出，pL的平均值为零 。
式（2.21）是欧姆定律的相量表达式。
2.2 单一参数的正弦交流；(c)相量图；(d)功率波形图
2.2 单一参数的正弦交流电路
2.功率关系 (1)瞬时功率 电阻任一瞬间吸收的功率称为瞬时功率，用小写字
母pR表示，它等于该瞬间电压uR和电流i的乘积
2.2 单一参数的正弦交流电路
（3）无功功率 用符号Q表示无功功率，即
(2.30)
无功功率的单位用乏（var）或千乏（kvar）表示。
2.2 单一参数的正弦交流电路
2.2.3 纯电容电路
在交流电压作用下，电容器两极板上的电压极性不断 地变化，电容器将周期性充电和放电，两极板上的电量也 随着发生变化，在电路中就会引起电流
(2.22)
2.2 单一参数的正弦交流电路
（2）平均功率
(2.23)
2.2 单一参数的正弦交流电路
2.2.2 纯电感电路
1.电压和电流的关系
2.2 单一参数的正弦交流电路
根据基尔霍夫定律有 设电流为参考相量，即 则
(2.24)
电压也是一个同频率的正弦量。
2.2 单一参数的正弦交流电路
图2.11 电感元件的交流电路 (a)电路图；(b)电压与电流的正弦波形；
（2.17）
2.2 单一参数的正弦交流电路
将式（2.17）代入式（2.16），得
2.2 单一参数的正弦交流电路
2.功率关系 (1)瞬时功率
(2.28)
电感电路中，瞬时功率是一个最大值是 ，并以2ω的 角频率随时间而变化的交变量，其波形如图2.11（d） 所示。
2.2 单一参数的正弦交流电路
(2)平均功率
(2.29)
从图2.11（d）的波形图也可看出，pL的平均值为零 。
式（2.21）是欧姆定律的相量表达式。
2.2 单一参数的正弦交流；(c)相量图；(d)功率波形图
2.2 单一参数的正弦交流电路
2.功率关系 (1)瞬时功率 电阻任一瞬间吸收的功率称为瞬时功率，用小写字
母pR表示，它等于该瞬间电压uR和电流i的乘积
2.2 单一参数的正弦交流电路
（3）无功功率 用符号Q表示无功功率，即
(2.30)
无功功率的单位用乏（var）或千乏（kvar）表示。
2.2 单一参数的正弦交流电路
2.2.3 纯电容电路
在交流电压作用下，电容器两极板上的电压极性不断 地变化，电容器将周期性充电和放电，两极板上的电量也 随着发生变化，在电路中就会引起电流
(2.22)
2.2 单一参数的正弦交流电路
（2）平均功率
(2.23)
2.2 单一参数的正弦交流电路
2.2.2 纯电感电路
1.电压和电流的关系
2.2 单一参数的正弦交流电路
根据基尔霍夫定律有 设电流为参考相量，即 则
(2.24)
电压也是一个同频率的正弦量。
2.2 单一参数的正弦交流电路
图2.11 电感元件的交流电路 (a)电路图；(b)电压与电流的正弦波形；
（2.17）
2.2 单一参数的正弦交流电路
将式（2.17）代入式（2.16），得
第8次课 单一参数交流电路教案
［例 3］ 把一个 0.1 H 的电感接到 10 V、50 HZ 的工频交流电源上，电流 是多少？若接到 10 V、5 000 HZ 的交流电源上，电流是多少？
解：（1）接到 10 V、50 HZ 的工频交流电源上
X L = 2π fL = 2π × 50 × 0.1 Ω = 31.4 Ω
课次 8
共7页
3．电压、电流有效值之间的关系：U = RI
4．电压、电流相量之间的关系
I& = I ∠0o
U& = U ∠0o
U& I&
=
U ∠0o I ∠0o
=U I
∠0o
= R∠0o
=
R
U& = RI&
U& 和 I& 的相位相同，如图 3.3.1（b）所示。
5．瞬时功率 p
p
=
ui
=
UmIm
sin 2
ωt
=
UmIm 2
课次 8
共7页
第4页
解：（1）接到 10 V、50 HZ 的工频交流电源上
XC
=1 2π fC来自=1 2π ×50 × 25×10−6
Ω = 127.4 Ω
I = U = 10 A = 0.078 A XC 127.4
Q = UI = 10× 0.078 var = 0.78 var
(2)接到 10 V、5 000 HZ 的交流电源上
=
UmIm
sin
ωt
cos ωt
=
Um Im 2
sin
2ωt
=
UI
sin
2ωt
7．平均功率 P
∫ ∫ P = 1
T pdt = 1
解：（1）接到 10 V、50 HZ 的工频交流电源上
X L = 2π fL = 2π × 50 × 0.1 Ω = 31.4 Ω
课次 8
共7页
3．电压、电流有效值之间的关系：U = RI
4．电压、电流相量之间的关系
I& = I ∠0o
U& = U ∠0o
U& I&
=
U ∠0o I ∠0o
=U I
∠0o
= R∠0o
=
R
U& = RI&
U& 和 I& 的相位相同，如图 3.3.1（b）所示。
5．瞬时功率 p
p
=
ui
=
UmIm
sin 2
ωt
=
UmIm 2
课次 8
共7页
第4页
解：（1）接到 10 V、50 HZ 的工频交流电源上
XC
=1 2π fC来自=1 2π ×50 × 25×10−6
Ω = 127.4 Ω
I = U = 10 A = 0.078 A XC 127.4
Q = UI = 10× 0.078 var = 0.78 var
(2)接到 10 V、5 000 HZ 的交流电源上
=
UmIm
sin
ωt
cos ωt
=
Um Im 2
sin
2ωt
=
UI
sin
2ωt
7．平均功率 P
∫ ∫ P = 1
T pdt = 1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
O
f
u2IωLsi(n ω t90) U超前 I90
可得相量式：U I U I 090 IωL90U
则： U I U I 90jL
U jI ω L I (X jL )
I
相量图
电感电路复数形式的欧姆定律
A
7
2. 功率关系
i 2Isinωt u2Iω Lsi(n ω t90 )
(1) 瞬时功率
ui
① 频率相同
② I =UC
ω t ③电流超前电压90
90
相位差 ψuψi 90
A
12
u 2Usinωt i2 U ω C si(n ω t90 )
有效值 IUωC 或 U 1 I
ωC
定义：
XC
1 1 ωC 2π f
C
容抗（Ω）
则: UI XC
1 XC 2π f C
直流：XC ，电容C视为开路
瞬时功率 ：piuUsIin 2ωt
QUII2XLU2XL
单位：var
例1: 把一个0.1H的电感接到 f=50Hz, U=10V的正弦
电源上，求I，如保持U不变，而电源
f = 5000Hz, 这时I为多少？
解： (1) 当 f = 50Hz 时
X L 2 f L 2 3 .5 1 0 0 4 . 3 1Ω 1.
i
瞬时功率在一个周期内的平均值
+
u
P1
T
pdt1
T
uidt
大写
T0
T0
T 10 T1 2U m Im (1 co2ω st)dt
p
_ p
R
P
1
T
U(I1 c
oω st)2d tUI
T0
O
ωt
PUII2R U 2 单位:瓦（W）
R
注意：通常铭牌数据或测量的功率均指有功功率。
A
4
2.3.2 电感元件的交流电路
T0
A
C是非耗 能元件
15
瞬时功率 ：piuUsIin 2ωt
u,i i u
o
i
+
u
i u+
-i u
-i u
- -++
p
结论： 纯电容不消
ωt
耗能量，只和 电源进行能量 交换（能量的 吞吐)。
+ p <0 + p <0
所以电容C是储
o
p >0
p >0
ωt 能元件。
充电 放电 充电 放电
A
16
(3) 无功功率 Q 为了同电感电路的无功功率相比较，这里也设
•
U A 0
1
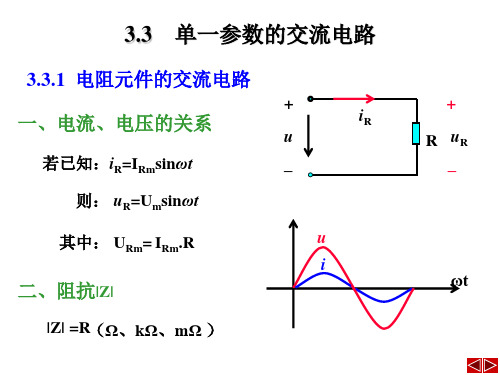
2.3.1 电阻元件的交流电路
1. 电压与电流的关系
i
根据欧姆定律: uiR
设 uUmsin ωt
+
u
R
_
iuU m siω nt 2Usiω nt RR R
Im siω n t2Isiω n t
① 频率相同
I
相量图 U
②大小关系：I U
相量式：
R
③相位关系 ： u、i 相位相同
II 0
u i
结论：
纯电感不消
o
ωt
耗能量，只和
i
+
u
i u
i u
i u+
- ++-
p
可逆的能量 转换过程
+ p <0 + p <0
o
p >0
p >0
电源进行能量 交换（能量的 吞吐)。
电感L是储 ωt 能元件。
储能 放能 储能 放能
A
9
(3) 无功功率 Q 用以衡量电感电路中能量交换的规模。用瞬时功率 达到的最大值表征，即
A
10
I U 10 318mA XL 31.4
（2）当 f = 5000Hz 时
X L 2 f L 2 3 .5 10 4 00 .3 1 0 1 Ω
I U 10 3.18mA XL 3140
所以电感元件具有通低频阻高频的特性
练习题： 1.一只L=20mH的电感线圈，通以
i5 2sin(t31 34 0)A 的电流
交流：f
XC
所以电容C具有隔直通交的作用
A
13
XC
1 2π fC
容抗XC是频率的函数
I , XC
XC
1 ωC
IU(2πfC)
由：u 2Usinωt
O
f
i2 U ω C si(n ω t90 )
可得相量式
UU 0 I I90jU ωC I
I超前 U90
则：UjIω1CjIXC
电容电路中复数形式的欧姆定律
1. 电压与电流的关系
基本关系式：ueL
设：i 2Isinωt
Ldi dt
i
+
-
u L eL
uLd(Imsi nωt) dt
-
+
2IωLsi(n ωt90 )
2Us i(n ωt90)
ui u i
① 频率相同
② U =I L
O
90
ωt ③ 电压超前电流90
相位差 ψuψi 90
A
5
i 2Isinωt
相位差：ui 0 U U0I R
A
2
2. 功率关系
(1) 瞬时功率 p：瞬时电压与瞬时电流的乘积
i 2 I sinω t
ui
iu
u 2Usinω t
小写
O
ωt
pui
UmImsi2nωt
pp
12UmIm(1co2sωt) O
ωt
结论: p 0 （耗能元件）,且随时间变化。
A
3
(2) 平均功率(有功功率)P
u2IωLsi(n ω t90)
有效值: UIωL
或 I U
L
定义： XLL2fL 感抗(Ω)
则: UI X L
XL2πfL 直流：f = 0, XL =0，电感L视为短路
交流：f
XL
电感L具有通直阻交的作用
A
6
XLωL2πfL
感抗XL是频率的函数
根据： i 2Isinωt
I, XL
I U
2fL XL
p iu U m I m sω its n ( i ω t n 9 )0 U m Im siω n tco ω t sU m 2 Im si2 ω n t
UsIin 2ωt
(2) 平均功率
P 1
T
pdt
To
1T
T o UIsi n(2ωt)dt 0
A
L是非耗 能元件
8
分析：瞬时功率 ：piuUsIin 2ωt夫定律
正弦电流电路中的各支路电流和支路电压都 是同频正弦量，所以可以用相量法将KCL和KVL 转换为相量形式。
1、基尔霍夫电流定律
对电路中任一点，根据KCL有 Σ i = 0
其相量形式为
•
I 0
2、基尔霍夫电压定律
对电路任一回路，根据KVL有 Σ u = 0
其相量形式为
U 相量图
A
14
2.功率关系
i
由 u 2Usinωt
+
i2 U ω C si(n ω t90 ) u_
C
(1) 瞬时功率
p iu U m I m sω its n ( i ω t n 9 )0
UmImsin2ωt (2) 平均2功率 Ｐ
UsIin 2ωt
P 1
T
pdt
T0
1
T
UIsin(2ωt)dt 0
求(1)感抗XL;(2)线圈两端的电压u; (3)有功功率和无功功率。
A
11
2.3.3 电容元件的交流电路
1.电流与电压的关系
基本关系式： i C du
设：u 2Usinωt dt
i
+
u
C
_
则：iCdu 2Uω Ccoω st 电流与电压
dt
的变化率成
2Uω Csiω nt (90 ) 正比。
ui