回归分析之分类变量的编码方法
回归分析中的变量转换技巧(Ⅱ)

回归分析是统计学中一种常见的数据分析方法,用于研究一个或多个自变量与因变量之间的关系。
在实际应用中,回归分析经常需要对变量进行转换,以满足模型的假设或改善模型的拟合效果。
本文将讨论回归分析中的变量转换技巧,包括对连续变量和分类变量的转换方法以及常见的应用场景。
**连续变量的转换**在回归分析中,连续变量是指可以在一定范围内取任意值的变量,例如年龄、收入等。
对于连续变量,常见的转换方法包括取对数、平方、开方等。
首先,对数转换是常用的一种方法。
当自变量或因变量的分布偏态严重时,取对数可以使数据更加符合正态分布,从而满足回归模型的假设。
例如,当因变量呈现指数增长的趋势时,可以对其取对数,使之线性化。
另外,对数转换还可以减少极端值的影响,提高模型的稳健性。
其次,平方和开方转换也是常见的方法。
当因变量和自变量之间存在非线性关系时,通过平方或开方转换可以使其线性化。
例如,当研究身高和体重之间的关系时,可以考虑对身高进行平方转换,以捕捉体重随身高变化的非线性趋势。
此外,还有其他一些转换方法,如倒数转换、指数转换等,可以根据具体情况选择合适的方法。
需要注意的是,转换后的变量需要与原始变量具有一定程度的线性关系,同时要避免过度转换导致模型失真。
**分类变量的转换**除了连续变量,回归分析中还常常涉及分类变量。
分类变量是指具有有限个取值的变量,例如性别、学历等。
对于分类变量,常见的转换方法包括虚拟变量编码、因子变量编码等。
首先,虚拟变量编码是最常用的方法之一。
虚拟变量编码将原始的分类变量转换为多个二元变量,用0和1表示。
例如,对于性别这一分类变量,可以通过虚拟变量编码将其转换为一个“男”变量和一个“女”变量,分别表示是否为男性和女性。
虚拟变量编码可以使分类变量在回归分析中更好地参与建模,同时避免了将分类变量视为连续变量的问题。
其次,因子变量编码是另一种常见的转换方法。
因子变量编码将原始的分类变量转换为数值型的因子变量,以便在回归分析中使用。
回归分析中的变量转换技巧(四)

回归分析是统计学中一种重要的分析方法,它用来研究自变量和因变量之间的关系。
在进行回归分析时,有时候需要对变量进行转换,以满足回归分析的前提条件或者改善模型的性能。
在这篇文章中,我将从常见的变量转换技巧入手,探讨回归分析中的变量转换技巧。
1. 自然对数转换自然对数转换是回归分析中常见的一种变量转换方法。
在实际数据分析中,很多变量的分布会呈现偏态分布或者右偏斜的特点,这时候可以考虑对自变量或者因变量进行自然对数转换。
自然对数转换可以将偏态分布的数据变换为近似正态分布,有助于提高模型的拟合效果和预测准确性。
2. 平方根转换平方根转换是另一种常见的变量转换方法。
当变量的分布呈现左偏斜或者右偏斜时,可以考虑对变量进行平方根转换。
平方根转换可以降低变量的偏度和峰度,使得变量更加接近正态分布,有利于改善模型的性能。
3. 反正弦转换反正弦转换是一种特殊的变量转换方法,它常用于处理百分比或比率等变量。
在回归分析中,有时候需要研究百分比或比率与因变量之间的关系,这时候可以考虑对百分比或比率进行反正弦转换。
反正弦转换可以将百分比或比率转换为角度,使得变量更加符合正态分布,有助于改善回归模型的拟合效果。
4. Box-Cox转换Box-Cox转换是一种广义的变量转换方法,它可以对各种类型的变量进行转换,包括正态分布、偏态分布和右偏斜分布等。
Box-Cox转换通过引入参数λ,对变量进行不同程度的幂次转换,使得变量更加接近正态分布。
Box-Cox转换可以根据数据的实际情况选择合适的参数λ,是一种非常灵活和有效的变量转换方法。
5. 分类变量的虚拟变量转换在回归分析中,经常会遇到分类变量(如性别、地区、学历等)的处理问题。
对于分类变量,常见的处理方法是引入虚拟变量。
虚拟变量转换可以将分类变量转换为二进制的0和1,以便于在回归模型中进行分析。
虚拟变量转换是回归分析中必不可少的一种技巧,可以有效地处理分类变量对模型的影响。
6. 离散化变量的分组转换除了连续变量的转换,回归分析中还需要处理离散化变量的转换。
二元、多元logistic回归分析

二元logistic回归分析1.理论Logistic回归模型:设因变量为Y,自变量为x1,x2,...,xn。
事件发生与不发生的概率比Pi /(1-pi)被称为事件发生比。
后对事件发生比做对数变换,能得到logistic回归的线性模式:ln(pi /(1-pi))=β+β1x1+...βnxn采用最大似然比法或者迭代法对参数的估计,参数通过似然比检验和Wold 检验。
二元logistic回归是指因变量为二分类变量时的回归分析。
在建立回归模型时,目标的取值范围在0-1之间。
常因变量为二分类数据自变量可以是连续型随机变量和分类数据图1数据类型2.重新编码操作步骤首先将数据导入spss中,数据情况如下图所示,首先先对变量进行重新编码处理。
图2数据情况第一步、点击转换、重新编码为相同的变量。
图3数据编码第一步第二步:进入图中变量框后,将需要处理的变量放入变量放入框中,后点击旧值和新值,在旧值中输入原有值,后在新值中输入新值,点击添加、继续。
图4数据编码第二步3.二元logistic回归分析操作步骤第一步:点击分析、回归、二元logistic。
图5二元logistic回归分析第一步第二步:进入图中对话框后将因变量、自变量放入对应变量框中,点击分类、进入定义分类变量框后。
将协变量框中的分类变量放入分类协变量框中(一般情况除二分类或有序分类数据不需哑变量设置),并进行哑变量的设置,点击继续。
图6第二步第三步:点击选项,勾选霍斯默-莱梅肖拟合优度、Exp(B)的置信区间、迭代历史记录。
点击继续、确定。
图7选项勾选4.二元logistic回归分析结果二元logistic回归分析的个案摘要、因变量编码、分类变量编码结果。
图8分类变量编码迭代历史记录、分类表、方程中的变量、未包括在方程中的变量结果。
图9块0:起始块迭代历史记录、模型中的Omnibus检验、模型摘要、霍斯默-莱梅肖检验。
图10块1:方法=输入分类表、方差中的变量结果。
在MATLAB中进行分类和回归分析

在MATLAB中进行分类和回归分析在科学和工程领域,分类和回归分析是常见的数据分析方法。
而MATLAB作为一种功能强大的数据分析软件,提供了丰富的工具和函数,使得分类和回归分析变得更加简单和高效。
本文将介绍在MATLAB中进行分类和回归分析的方法和技巧,帮助读者更好地理解和应用这些技术。
一、背景介绍分类和回归分析是基于已知数据的模式进行预测和分类的统计方法。
分类分析用于将数据分为不同的类别,而回归分析则试图通过已知数据的模式预测未知数据的数值。
这些方法在各个领域都有广泛的应用,如金融、医疗、市场营销等。
二、数据准备在进行分类和回归分析之前,需要准备好相应的数据。
一般来说,数据应当包含自变量(也称为特征或输入)和因变量(也称为标签或输出)。
自变量是用来作为预测或分类的输入变量,而因变量是要预测或分类的目标变量。
通常情况下,数据应当是数值型的,如果包含分类变量,需要进行相应的编码或处理。
三、分类分析在MATLAB中进行分类分析,有多种方法和技术可供选择。
其中最常见的方法包括K最近邻算法(K-nearest neighbors)和支持向量机(Support Vector Machines)等。
这些方法都有相应的函数,可以用于在MATLAB中实现分类分析。
K最近邻算法基于训练样本和测试样本之间的距离,将测试样本分类为与其最近的K个训练样本所属的类别。
而支持向量机则试图找到一个超平面,将不同类别的样本分开,并使得分类误差最小化。
在MATLAB中,我们可以使用fitcknn和fitcsvm函数来实现K最近邻算法和支持向量机。
除了上述方法,还有其他的分类算法可以在MATLAB中使用,如决策树、随机森林等。
根据数据的具体情况和需求,选择适合的分类算法非常重要。
四、回归分析在进行回归分析时,我们需要首先选择适当的回归模型。
常用的回归模型包括线性回归、多项式回归、岭回归等。
根据数据的分布和特点,选择合适的回归模型能够提高分析的准确性。
如何用SPSS做logistic回归分析解读
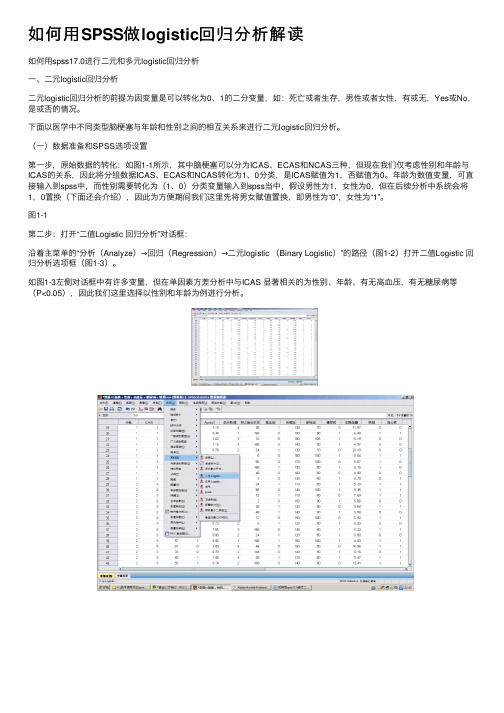
如何⽤SPSS做logistic回归分析解读如何⽤spss17.0进⾏⼆元和多元logistic回归分析⼀、⼆元logistic回归分析⼆元logistic回归分析的前提为因变量是可以转化为0、1的⼆分变量,如:死亡或者⽣存,男性或者⼥性,有或⽆,Yes或No,是或否的情况。
下⾯以医学中不同类型脑梗塞与年龄和性别之间的相互关系来进⾏⼆元logistic回归分析。
(⼀)数据准备和SPSS选项设置第⼀步,原始数据的转化:如图1-1所⽰,其中脑梗塞可以分为ICAS、ECAS和NCAS三种,但现在我们仅考虑性别和年龄与ICAS的关系,因此将分组数据ICAS、ECAS和NCAS转化为1、0分类,是ICAS赋值为1,否赋值为0。
年龄为数值变量,可直接输⼊到spss中,⽽性别需要转化为(1、0)分类变量输⼊到spss当中,假设男性为1,⼥性为0,但在后续分析中系统会将1,0置换(下⾯还会介绍),因此为⽅便期间我们这⾥先将男⼥赋值置换,即男性为“0”,⼥性为“1”。
图1-1第⼆步:打开“⼆值Logistic 回归分析”对话框:沿着主菜单的“分析(Analyze)→回归(Regression)→⼆元logistic (Binary Logistic)”的路径(图1-2)打开⼆值Logistic 回归分析选项框(图1-3)。
如图1-3左侧对话框中有许多变量,但在单因素⽅差分析中与ICAS 显著相关的为性别、年龄、有⽆⾼⾎压,有⽆糖尿病等(P<0.05),因此我们这⾥选择以性别和年龄为例进⾏分析。
在图1-3中,因为我们要分析性别和年龄与ICAS的相关程度,因此将ICAS选⼊因变量(Dependent)中,⽽将性别和年龄选⼊协变量(Covariates)框中,在协变量下⽅的“⽅法(Method)”⼀栏中,共有七个选项。
采⽤第⼀种⽅法,即系统默认的强迫回归⽅法(进⼊“Enter”)。
接下来我们将对分类(Categorical),保存(Save),选项(Options)按照如图1-4、1-5、1-6中所⽰进⾏设置。
类别变量的回归方程

在回归分析中,自变量可以是连续的(数值型)或离散的(类别型)。
类别变量是一种离散变量,通常用于表示分类数据,例如性别(男/女)、国籍(中国/美国/其他)、婚姻状态(已婚/未婚)等。
当我们处理类别变量时,线性回归方程可能不适用,因为类别变量是非数值型的。
然而,我们可以使用逻辑回归(Logistic Regression)来处理类别变量。
逻辑回归是一种用于预测二分类因变量的统计方法。
它的基本思想是通过一个逻辑函数将自变量与因变量连接起来,然后使用最大似然估计法估计参数。
逻辑回归的数学模型如下:
P(Y=1) = 1 / (1 + exp(-(β0 + β1X1 + β2X2 + ... + βnXn)))
其中:
•P(Y=1) 是因变量为1的概率
•β0, β1, β2, ..., βn 是模型的参数
•X1, X2, ..., Xn 是自变量
•exp() 是自然指数函数
在Python中,可以使用sklearn库中的LogisticRegression类来拟合逻辑回归模型。
以下是一个简单的示例:
需要注意的是,逻辑回归假设因变量是二分类的,且自变量和因变量之间的关系是线性关系。
如果这些假设不成立,可能需要使用其他方法来处理类别变量。
stata 分类变量回归

stata 分类变量回归在Stata中,进行分类变量回归可以通过使用回归分析的命令来实现。
在回归模型中,分类变量通常需要进行虚拟变量编码,也称为哑变量编码,以便将其纳入回归模型中。
以下是在Stata中进行分类变量回归的一般步骤:1. 创建虚拟变量:首先,你需要将分类变量转换为虚拟变量。
在Stata中,你可以使用命令 "tabulate" 来查看分类变量的不同取值,并使用 "tabulate" 命令后面加上 "generate" 选项来生成虚拟变量。
例如,如果你的分类变量是 "group",你可以使用以下命令来生成虚拟变量:tabulate group, generate(group_dummy)。
2. 运行回归分析:一旦生成了虚拟变量,你可以将这些变量与其他自变量一起纳入回归模型中。
使用 "regress" 命令可以进行最小二乘回归分析。
例如,如果你的因变量是 "y",自变量包括连续变量 "x" 和虚拟变量 "group_dummy1" 和 "group_dummy2",你可以使用以下命令进行回归分析:regress y x group_dummy1 group_dummy2。
3. 解释结果,在得到回归结果后,你需要解释虚拟变量的系数。
系数表示了每个虚拟变量对因变量的影响。
通常,虚拟变量的系数表示了该变量相对于参照组的影响。
此外,在Stata中还有其他一些用于处理分类变量的命令,如"xi" 命令用于创建虚拟变量,以及 "tabulate" 命令用于查看分类变量的分布情况。
在进行分类变量回归时,还需要考虑模型的适配性、残差分析等问题,以确保回归模型的有效性和准确性。
总之,通过以上步骤,你可以在Stata中进行分类变量回归分析,并得到相应的回归结果和解释。
逻辑回归 类别变量和连续变量的交互对分类变量的解释-概述说明以及解释

逻辑回归类别变量和连续变量的交互对分类变量的解释-概述说明以及解释1.引言1.1 概述在统计学和机器学习领域中,逻辑回归是一种常用的分类算法。
它可以用来预测二分类问题,并且广泛应用于各种领域,包括医疗、金融、市场营销等。
然而,在实际应用中,我们经常会遇到同时包含类别变量和连续变量的数据集。
这就引发了一个问题:类别变量和连续变量之间是否存在某种交互作用,对逻辑回归模型的分类结果是否有影响?本文将探讨类别变量和连续变量之间的交互作用,并研究其对逻辑回归模型的解释能力的影响。
我们将详细介绍逻辑回归的原理和算法,并分析交互作用对分类变量解释能力的影响。
通过实证研究和数据分析,我们将提供一些有关如何处理类别变量和连续变量交互的实用技巧和建议。
文章的结构如下:引言部分将对逻辑回归、类别变量和连续变量进行简要介绍,并明确文章的目的。
接着,在正文部分,我们将详细讨论类别变量和连续变量的交互作用,并介绍如何解释逻辑回归模型中的分类变量。
最后,在结论部分,我们总结了本文的主要内容,并探讨了研究结果的意义。
通过本文的阅读,读者将了解到类别变量和连续变量的交互作用对逻辑回归模型的影响,并可以在实际应用中更准确地解释和使用逻辑回归模型。
此外,本文的研究结果还具有一定的理论和实践意义,对相关领域的学术研究和实际工作具有一定的参考价值。
1.2文章结构文章结构部分的内容可以包括以下信息:在本篇论文中,将探讨逻辑回归模型中类别变量和连续变量的交互对分类变量的解释的影响。
首先,将介绍逻辑回归模型和其在分类问题中的应用。
逻辑回归模型是一种常用的统计学习方法,广泛应用于二元分类问题。
它使用逻辑函数来建模分类变量,通过最大似然估计方法来估计模型的参数,从而预测分类结果。
然后,将详细讨论类别变量和连续变量的交互对逻辑回归模型的影响。
在实际问题中,常常会遇到一些特征既包括类别变量又包括连续变量的情况。
类别变量表示不同类别之间的差异,而连续变量表示数值上的差异。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b
k kYk 2
kk
其他编码方式:虚无编码
•“control” or “comparison” group coded 0 •“treatment” or “target” group coded 1
“conceptually”...
Group dc1 dc2
1
1
0
2
0
1
3*
0
0
* = comparison group
k
模型A:
=76.68+8.33Xi1+5.0Xi2
回归系数与预测值的解释。
模型检验
相对照的模型:
模型C: Ŷi = β0 模型A: Ŷi = β0 + β1Xi1 + β2Xi2
检验的虚无假设:
H0: β1 = β2 = 0 (Model comparison approach)
编码值
1
2
3
λ 1k
m-1 -1
-1
λ 2k
0
m-2 -1
λ3k
0
0
m-3
… m-2
m-1
m
… -1
-1
-1
… -1
-1
-1
… -1
-1
-1
λ6k
0
0
0
…2
-1
-1
λ7k
0
0
0
…0
1
-1
回归系数的解释
截距是两个组均值的简单平均数:
b1
Y1
Y2 2
b0
Y1
Y2 2
斜率是两组均值之差的平均:
整合上述结果
变异来源分析表
来源
组间 Xi1 Xi2
组内
总变异
b
SS
3733.3 8.33 3333.3 5.00 400.0
1800.0
5533.3
df
MS F
PRE
2 1866.7 21.778 .675 1 3333.3 38.895 .650 1 400.0 4.667 .182 21 85.7
“conceptually”...
Group ec1 ec2
1
1
0
2
0
1
3*
-1 -1
* = comparison group
For several participants...
Case group ec1 ec2
1
1
1
0
2
1
1
0
3
2
0
1
4
2
0
1
5
3
-1
-1
6
3
-1
-1
如果一侧变量存在2个以上的水平?
某研究者想考察心理表象对记忆的影响。他考察了两种实 验条件下三组被试对词语的正确回忆的同时呈现图片 控制组:直接记忆这两个词
任务:狗,自行车
实验组1
请想象一条狗骑 着自行车
实验组2
正确回忆率
控制组 60 70 70 40 60 50 70 60 60
For several participants...
Case group dc1 dc2
1
1
1
0
2
1
1
0
3
2
0
1
4
2
0
1
5
3
0
0
6
3
0
0
其他编码方式:效应编码
• “control” or “comparison” group coded -1 •“treatment” or “target” group coded 1
SPSS结果
Source Source Source (SPSS) (ANOVA)
SSR Regression Between
SSE(A) Residual Within
SSE(C) Total
Total
SS df MS
3733.33 2 1866.67 1800.00 21 85.71 5533.33 23
REGRESSION /DESCRIPTIVES MEAN STDDEV CORR SIG N /MISSING LISTWISE /STATISTICS COEFF OUTS R ANOVA /CRITERIA=PIN(.05) POUT(.10) /NOORIGIN /DEPENDENT willing /METHOD=ENTER x1 x2 .
F
Sig.
21.78 .000
更细节性的检验每一对照编码
To test contrast 1:
模型C: Ŷi = β0 + β2Xi2 模型A: Ŷi = β0 + β1Xi1 + β2Xi2
Null Hypothesis:
H0: β1 = 0
or
H0 : μ1 = (μ2 + μ3)/2
SSR
(( k k kk2Y/
k)2 nk)
SSRC1 (( k k kk2Y/ kn)k) 2 8(.-32*3630+80+90)^2/(6/8)=3333.3 SSRC2 (( k k kk2Y/ kn)k) 2 1(.9000-80)^2/(2/8)=400
回归分析之九
回顾:对比性编码
分类变量作为预测变量时一个重要的问题是如何解释结 果,为此需要编码。
对比性编码是众多编码方式中比较简单的一种,更为关 键的是这个编码可以比较灵活地回答我们的研究问题。
对比性编码要满足两个条件: 对于经过对比编码后的预测变量,其所有取值之和 为零; 如果存在两个以上经过编码的变量,这些变量相互 正交。
如何知道各编码变量相互正交
12kk Code 1: λ11= -2; λ12= +1; λ13= +1 Code 2: λ21= 0; λ22= -1; λ13= +1
Code 1和Code 2直观含义?
系列1 系列2
控制组
-2 0
-1 0
联想组
1 -1
0 -1
图片组
1 1
1 1
1k 2k 0
or
H0 : μ1 = μ2 = μ3 (ANOVA approach)
SPSS程序
RECODE feedback (1=-2) (ELSE=1) INTO x1 . VARIABLE LABELS x1 'contrast coding 1'. EXECUTE .
RECODE feedback (1=0) (2=-1) (3=1) INTO x2 . VARIABLE LABELS x2 'contrast coding 2'. EXECUTE .
联想组 80 70 70 90 80 70 100 80 80
图片组 90 85 85 100 90 85 90 95 90
对比编码问题
这时不能只用一个预测变量,因为结果无从解释。
对于分类变量,应当有(m-1)个对比编码
回忆对比编码的两个条件 同一编码的所有取值的和为零; 各个编码之间相互正交
