齿轮螺旋角计算方式(学校教学)
机械原理齿轮计算的相关公式

机械原理齿轮计算的相关公式齿轮计算公式节圆柱上的螺旋角:L d /tan 00?=πβ 基圆柱上的螺旋角:n g αββcos sin sin 0?= 齿厚中心车角:Z θ/90?= 销子直径:m 728.1dp ?=中心距离增加系数:)1cos /(cos )2/)((y b 021-?+=ααZ Z标准正齿轮的计算(小齿轮①,大齿轮②)1.齿轮齿标准 2.工齿齿形直齿 3.模数 m4.压力角c αα=05.齿数 21,Z Z6.有效齿深 m 2h e ?= 7.全齿深 c m h +=28.齿顶隙 m 35.0,m 25.0,m 2.0c =9.基础节圆直径 m d 0?=Z10.外径 m )2(d k ?+=Z11.齿底直径 c 2m )2(d r ?-?-=Z12.基础圆直径0g cos m d αZ ??=13.周节m t 0?=π14.法线节距0e cos m t απ??= 15.圆弧齿厚2/m S 0?=π16.弦齿厚)2sin(m S 1j Z πZ =17.齿轮油标尺齿高 m m h j +Z-??Z =)2cos1()2/(π18.跨齿数 5.0)180/(0m=Z αZ19.跨齿厚 ])5.0([cos 0o m inva m m S Z ?-?Z ??=πα 20.销子直径 m 728.1d ?=21.圆柱测量尺寸d m d m +?Z =)cos /cos (0φα (偶数齿)d )]90(cos)cos /cos m [(d 0m +?=ZφαZ (奇数齿)其中, 00)2cos (1απαφinv m dinv +-Z22.齿隙 f ?移位正齿轮计算公式(小齿轮①,大齿轮②)1.齿轮齿形转位 2.工具齿形直齿3.模数 m4.压力角c αα=05.齿数 Z6.有效齿深 m 2h e ?=7.全齿深 c m )]x x (y 2[h 21+??-+= 或 c m 2h +?=8.齿隙 c9.转位系数 x10.中心距离m y x ?+=αα11.基准节圆直径m d 0?=Z12.啮合压力角021210b inv )x x (tan 2inv αZZ αα+++?=13.啮合节圆直径)(x 2d 211b Z Z Z α+??=14.外径 m )x y (2m )2(d 21k ?-?+?+=Z 15.齿顶圆直径h 2d d 1k r ?-=16.基圆直径0cos t g m d α??Z =17.周节m t 0?=π18.法线节距00cos m t απ??= 19.圆弧齿厚010tan m x 22mS απ=20.弦齿厚)tan x 2x 2sin(m S 1111j Z απZ ??+=21.齿轮游标尺齿高2d d )]tan x 22cos(1[2mh 110k 1111j -++-??=Z αZ πZ22.跨齿数 5.0180x 1b m 1+?=αZ23.跨齿厚 01m sin m x 2)(S 1α+=标准齿轮的齿厚24.梢子直径m 728.1d 1?=25.圆柱测量尺寸110cos cos 1d m d m +??Z =φα (偶数齿)111)90cos(cos cos 1d m d m +Z Z =φα (奇数齿)11011i1tan x 2)inv 2(cos m d inv Z ααZ παZ Φ??+-?-??=26.标准螺旋齿的计算公式(齿直角方式)(小齿轮①,大齿轮②) 1. 齿轮齿形标准 2. 齿形基准断面齿直角 3. 工具齿形螺旋齿4. 模数 n c m m =5. 压力角n 0c ααα==6. 齿数 1Z7. 螺旋角方向0β(左或右)8. 有效齿深 n e m 2h ?= 9.全齿深c m 2h n +?=10. 正面压力角n1s cos m tan βZ α?=11. 中心距离n21cos 2m )(βZ Z α??+=12. 基准节圆直径n10cos m d βZ ?=13. 外径 n 01k m 2d d ?+= 14. 齿底圆直径)c m (2d d n 01r ++=15. 基圆直径gnn 1g cos cos m d 1βαZ ??=16. 基圆上的螺旋角n 0g cos sin sin αββ?=17. 导程1001cot d L 1βπ??=18. 周节(齿直角)n n 0m t ?=π19. 法线节距(齿直角)n n en cos m t απ??= 20. 圆弧齿厚(齿直角) 2m S nn 0?=π21. 相当正齿轮齿数101cos βZ Z =22. 弦齿厚 )2sin(m S 1v n 1v j 1ZπZ=23. 齿轮游标尺齿深n 1v n1v 1j m )2cos1(2m h +?-??=ZπZ24. 跨齿数 5.01801v n m 1+?=ZαZ25. 跨齿厚]inv )5.0m ([cos m S s 11n n m 1αZ Z πα?+-=26. 梢子直径)2(cos 1111n v n v n inv inv m d απφα-Z ?+Z ?=其中,)(2tan 11Rad inv n v n απαφ-Z ?+=27. 圆柱测量尺寸110cos cos 1d m d m +??Z =φα (偶数齿)111)90cos(cos cos 1d m d m +Z Z =φα (奇数齿)110111tan 2)2(cos Z ??+-Z ?-??Z =ααπαφx inv m d inv i28. 齿隙 f移位螺旋齿的计算公式(齿直角方式)(小齿轮①,大齿轮②)1. 齿轮齿形移位 2. 齿形基准断面齿直角 3. 工具齿形螺旋齿4. 模数(齿直角) n c m m =5. 压力角(齿直角) 0a a a c n -=6. 齿数 1Z7. 螺旋方向0β8. 有效齿深 n e m h 2= 9. 全齿深 c m h n +=2 10. 移位系数 1n x11. 中心距离n x ym a a +=12. 正面模数 0cos βn s m m =13. 正面压力角cos tanβans m =14. 相当正齿轮齿数311β?s z z v =15. 齿直角啮齿压力角 anv v n n ann a invz z x x b inv +++=2121tan216. 基准节圆直径011cos βn o m z d =17. 外径n n n n k m x m m z d 101122cos ++=β18. 啮齿节圆直径)(22111z z z a d x b +=19. 基圆直径gnn g a m z d βcos cos 11?=20. 基础圆柱上的螺旋角 n og a cos sin sin ββ=21. 圆弧齿厚n n n on m a x s ??+=)tan 22 (1π22. 弦齿厚)tan 22sin(11111v on v n v j z a x z m z s+=π23. 齿轮游标尺齿高2)}tan 22cos(1{21111111o k v on v nv d d z a x z m z hj -++-?=π24. 跨齿数 5.018011+=v n m z ab z25. 跨齿厚111sin 2n n n m a m x s ??+=)(标准螺旋齿轮的齿厚销子直径近似值=1d26圆柱测量尺寸/1111cos cos da m z d ss m +?=φ(偶数齿)/1111190coscos cos d z a m z d ss m +?=φ111111tan 2)2(cos z a x inva z a m z d in nn s nn ?+--='πφ注:齿隙 f=m 1.25以下 0.025-0.075 m 1.25-2.5 0.05-0.10 ))*25.2((tan 2)2( cos 22111111m r rL z a x inva z a m z d in nn s nn ---?+--='πφ。
齿轮基本计算公式

齿轮计算公式节圆柱上的螺旋角:L d /tan 00⋅=πβ 基圆柱上的螺旋角:n g αββcos sin sin 0⋅= 齿厚中心车角:Z θ/90︒= 销子直径:m 728.1dp ⋅=中心距离增加系数:)1cos /(cos )2/)((y b 021-⋅+=ααZ Z标准正齿轮的计算(小齿轮①,大齿轮②)1. 齿轮齿 标准 2. 工齿齿形 直齿 3. 模数 m 4. 压力角 c αα=0 5. 齿数 21,Z Z6. 有效齿深 m 2h e ⋅=7. 全齿深 c m h +=28. 齿顶隙 m 35.0,m 25.0,m 2.0c ⋅⋅⋅=9. 基础节圆直径 m d 0⋅=Z 10. 外径 m )2(d k ⋅+=Z 11. 齿底直径 c 2m )2(d r ⋅-⋅-=Z12. 基础圆直径 0g cos m d αZ ⋅⋅= 13. 周节 m t 0⋅=π 14. 法线节距 0e cos m t απ⋅⋅= 15. 圆弧齿厚2/m S 0⋅=π16. 弦齿厚)2sin(m S 1j Z πZ ⋅⋅⋅= 17. 齿轮油标尺齿高 m m h j +Z⋅-⨯⋅Z =)2cos1()2/(π18. 跨齿数5.0)180/(0m ⨯⋅=Z αZ19. 跨齿厚 ])5.0([cos 0o m inva m m S Z ⨯-⋅Z ⋅⋅=πα20. 销子直径 m 728.1d ⋅=21. 圆柱测量尺寸 d m d m +⋅Z =)cos /cos (0φα (偶数齿)d )]90(cos)cos /cos m [(d 0m +︒⨯⋅=ZφαZ (奇数齿)其中, 00)2cos (1απαφinv m d inv +-⋅Z 22. 齿隙f ?移位正齿轮计算公式(小齿轮①,大齿轮②)1. 齿轮齿形 转位 2. 工具齿形 直齿 3. 模数 m 4. 压力角 c αα=05. 齿数 Z6. 有效齿深 m 2h e ⋅=7. 全齿深 c m )]x x (y 2[h 21+⋅⋅-+= 或 c m 2h +⋅=8. 齿隙 c 9. 转位系数 x10. 中心距离 m y x ⋅+=αα11. 基准节圆直径m d 0⋅=Z12. 啮合压力角021210b inv )x x (tan 2inv αZ Z αα+++⋅=13. 啮合节圆直径)(x 2d 211b Z Z Z α+⋅⋅=14. 外径 m )x y (2m )2(d 21k ⋅-⋅+⋅+=Z15. 齿顶圆直径 h 2d d 1k r ⋅-=16. 基圆直径 0cos t g m d α⋅⋅Z = 17. 周节 m t 0⋅=π 18. 法线节距00cos m t απ⋅⋅=19. 圆弧齿厚 010tan m x 22mS απ⋅⋅⋅⋅⋅=20. 弦齿厚)tan x 2x 2sin(m S 1111j Z απZ ⋅⋅+⋅⋅⋅=21. 齿轮游标尺齿高2d d )]tan x 22cos(1[2mh 110k10111j -+⋅⋅+⋅-⋅⋅=Z αZ πZ 22. 跨齿数 5.0180x 1b m 1+⋅=αZ23. 跨齿厚 01m sin m x 2)(S 1α⋅⋅⋅+=标准齿轮的齿厚 24. 梢子直径m 728.1d 1⋅=25. 圆柱测量尺寸11cos cos 1d m d m +⋅⋅Z =φα (偶数齿)1110)90cos(cos cos 1d m d m +Z ︒⋅⋅⋅Z =φα (奇数齿)1010101i 1tan x 2)inv 2(cos m d inv Z ααZ παZ Φ⋅⋅+-⋅-⋅⋅=标准螺旋齿的计算公式(齿直角方式)(小齿轮①,大齿轮②)1. 齿轮齿形 标准2. 齿形基准断面 齿直角3. 工具齿形 螺旋齿4. 模数 n c m m =5. 压力角 n 0c ααα==6. 齿数 1Z7. 螺旋角方向 0β(左或右)8. 有效齿深 n e m 2h ⋅=9.全齿深c m 2h n +⋅=10. 正面压力角n1s cos m tan βZ α⋅=11. 中心距离n21cos 2m )(βZ Z α⋅⋅+=12. 基准节圆直径n10cos m d βZ ⋅=13. 外径 n 01k m 2d d ⋅+= 14. 齿底圆直径 )c m (2d d n 01r ++= 15. 基圆直径gnn 1g cos cos m d 1βαZ ⋅⋅=16. 基圆上的螺旋角 n 0g cos sin sin αββ⋅= 17. 导程1001cot d L 1βπ⋅⋅=18. 周节(齿直角)n n 0m t ⋅=π19. 法线节距(齿直角) n n en cos m t απ⋅⋅= 20. 圆弧齿厚(齿直角) 2m S nn 0⋅=π21. 相当正齿轮齿数101cos βZ Z =22. 弦齿厚)2sin(m S 1v n 1v j 1Z πZ ⋅⋅⋅=23. 齿轮游标尺齿深n 1v n1v 1j m )2cos 1(2m h +⋅-⋅⋅=Z πZ24. 跨齿数 5.01801v n m 1+⋅=Z αZ25. 跨齿厚]inv )5.0m ([cos m S s 11n n m 1αZ Z πα⋅+-⋅⋅⋅=26. 梢子直径)2(cos 1111n v n v n inv inv m d απφα-Z ⋅+⋅Z ⋅=其中,)(2tan 11Rad inv n v n απαφ-Z ⋅+=27. 圆柱测量尺寸11cos cos 1d m d m +⋅⋅Z =φα (偶数齿)1110)90cos(cos cos 1d m d m +Z ︒⋅⋅⋅Z =φα (奇数齿)10101011tan 2)2(cos Z ⋅⋅+-Z ⋅-⋅⋅Z =ααπαφx inv m d inv i 28. 齿隙f移位螺旋齿的计算公式(齿直角方式)(小齿轮①,大齿轮②)1. 齿轮齿形 移位2. 齿形基准断面 齿直角3. 工具齿形 螺旋齿4. 模数(齿直角) n c m m =5. 压力角(齿直角) 0a a a c n -=6. 齿数 1Z7. 螺旋方向 0β8. 有效齿深 n e m h 2= 9. 全齿深 c m h n +=2 10. 移位系数 1n x11. 中心距离n x ym a a +=12. 正面模数0cos βns m m =13. 正面压力角0cos tan βans m =14. 相当正齿轮齿数311βϑs z z v =15. 齿直角啮齿压力角an v v n n ann a inv z z x x b inv +++=2121t an 216. 基准节圆直径11cos βno m z d =17. 外径n n n nk m x m m z d 101122cos ++=β18. 啮齿节圆直径)(22111z z z a d x b +=19. 基圆直径gnn g a m z d βcos cos 11⋅=20. 基础圆柱上的螺旋角 n o g a cos sin sin ββ=21. 圆弧齿厚 n n n on m a x s ⋅⋅+=)tan 22(1π22. 弦齿厚 )t an 22sin(11111v on v n v j z a x z m z s ⋅+⋅⋅=π23. 齿轮游标尺齿高2)}t an 22cos(1{21111111o k v o n v n v d d z a x z m z hj -+⋅+-⋅=π24. 跨齿数 5.018011+=v n m z ab z25. 跨齿厚111sin 2n n n m a m x s ⋅⋅+=)(标准螺旋齿轮的齿厚 26. 销子直径 近似值=1d27. 圆柱测量尺寸/1111cos cos d a m z d ss m +⋅=φ(偶数齿)/1111190cos cos cos d z a m z d s s m +⋅= φ111111tan 2)2(cos z a x inva z a m z d in n n s n n ⋅+--='πφ 注:齿隙f=m 1.25以下 0.025-0.075m 1.25-2.5 0.05-0.10))*25.2((tan 2)2(cos 22111111m r r L z a x inva z a m z d in n n s n n ---⋅+--='πφ。
齿轮各部分计算公式
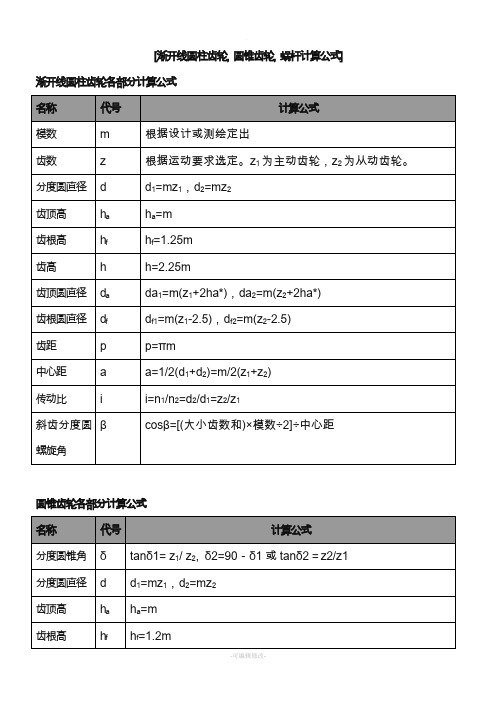
df
df1=m(z1-2.5),df2=m(z2-2.5)
齿距
p
p=πm
中心距
a
a=1/2(d1+d2)=m/2(z1+z2)
传动比
i
i=n1/n2=d2/d1=z2/z1
斜齿分度圆螺旋角
β
cosβ=[(大小齿数和)×模数÷2]÷中心距
圆锥齿轮各部分计算公式
名称
代号
计算公式
分度圆锥角
δ
tanδ1= z1/ z2,δ2=90-δ1或tanδ2=z2/z1
导程
p2
p2=πmz1
标准模数与蜗杆的直径系数
m/mm
1
1.25
1.6
2
q
18
16
17.9
1.25
17.5
9
11.2
14
17
m(q)
2.5(8.9,11.2,14.2,18)
3.15(8.8,11.2,14.2,17.7)
4(7.8,10,12.5,17.7)
5(8,10,12.6,18)
蜗轮各部分计算公式
名称
代号
计算公式
分度圆直径
d2
d1=mz2
齿顶高
ha2
ha1=m
齿根高
hf2
hf2=1.2m
齿高
h2
h2=ha2+ hf2=2.2m
喉圆直径
da2
da2=d2+2ha2=m(z2+2)
齿根圆直径
df2
df2=d2-2 hf2=m(z2-2.4)
轴向齿距
px
px=πm
导程角
γ
齿轮螺旋角计算公式

齿轮螺旋角计算公式
1关于齿轮螺旋角的计算公式
齿轮螺旋角是确定齿轮传动系统传递功率的重要参数,属于机械传动方面的基础知识。
齿轮螺旋角就是两个安装相邻轮毂的齿轮上,齿面在旋转过程中所形成螺旋形状所对应的夹角。
求取两个安装相邻轮毂的齿轮之间的齿轮螺旋角计算公式如下:
螺旋角α=(齿轮齿数z2-z1)π/z1z2
其中,z1为第一个齿轮的齿数,z2为第二个齿轮的齿数。
另外,根据齿轮传动的特点,轴上的轮毂应当以弹性关系相连,只有在定位和支承时才以传导热量和阻抗结构分开,因此在确定齿轮螺旋角时,要保证贴合度,轮毂的位置和可动性的定位应该具备一定的松偶合程度。
2如何求取一组齿轮传动系统的齿轮螺旋角
如果要确定一组齿轮传动系统的齿轮螺旋角,首先要获取每个齿轮的齿数参数,然后根据计算公式求取两个安装相邻轮毂的齿轮之间的齿轮螺旋角,依次递推至齿轮传动系统最后一个齿轮。
在求取螺旋角时,需要注意的是,一般在轮毂轴端会有限制位,确保轮毂可以正常旋转,而且要确定一定的阻尼用来减少非平衡情况下发生的转矩波动,以及限制在某个范围内的机械冲击情况。
以上就是关于齿轮螺旋角的计算公式以及如何求取一组齿轮传动系统的齿轮螺旋角的内容,了解这些基础知识可以使我们更熟悉机械传动的基本原理,避免在机械传动系统的设计和制造中出现不经预料的故障。
螺旋齿轮参数计算公式

螺旋齿轮参数计算公式
螺旋齿轮是一种常见的传动装置,它由蜗杆和蜗轮组成,适用于高速低扭矩的传动。
设计螺旋齿轮需要考虑多个参数,下面我们来介绍一下螺旋齿轮参数的计算公式。
1. 蜗杆转速计算公式
蜗杆的转速是设计螺旋齿轮时需要考虑的一个关键参数。
蜗杆转速计算公式如下:
n1 = n2/i
其中,n1为蜗杆转速;n2为蜗轮转速;i为蜗轮减速比。
2. 蜗杆负载计算公式
蜗杆的负载是指传给蜗杆的力矩,通常需要通过计算来确定。
蜗杆负载计算公式如下:
T1 = (9550 P)/n1
其中,T1为蜗杆负载;P为传动功率;n1为蜗杆转速。
3. 螺旋角计算公式
螺旋角是指蜗杆螺旋线与蜗轮轴线之间的夹角。
螺旋角的计算公式如下:
tan α2 = z2/(πd2)
其中,α2为螺旋角;z2为蜗轮齿数;d2为蜗轮节圆直径。
4. 螺旋齿计算公式
螺旋齿计算公式是设计螺旋齿轮时必不可少的公式之一,它用来确定蜗轮的齿数。
螺旋齿计算公式如下:
z2 = (d1 tan α1)/π
其中,z2为蜗轮齿数;d1为蜗杆节圆直径;α1为蜗杆螺旋角。
5. 其他参数计算公式
除上述参数外,设计螺旋齿轮还需要考虑其他参数,如模数、齿距、齿顶高等。
这些参数的计算公式需要根据具体情况确定,并结合实际生产需要进行调整。
综上所述,螺旋齿轮的参数计算公式是设计螺旋齿轮必不可少的工具之一,不同的参数相互关联,需要综合考虑。
在实际应用中,设计人员需要根据具体用途和工作条件进行特别设计,以确保螺旋齿轮的可靠性和性能。
螺旋下刀角度计算公式

螺旋下刀角度计算公式
螺旋角度计算公式D=L / π,基圆柱面上,圆柱螺旋线的切线与通过切点的圆柱面直母线之间所夹的锐角,称为基圆柱螺旋角。
变齿厚(斜)齿轮端截面的齿厚沿轴向是线性变化的,从而导致齿侧产生一个附加的螺旋角,左右齿面的分圆螺旋角和基圆螺旋角也相应改变。
因此有必要对其进行计算与直齿圆柱齿轮相比,由于斜齿圆柱齿轮具有承载能力强、传动平稳、冲击和噪声小等优点,因而得到广泛的应用。
一般来讲,若一对相互啮合轴线平行的斜齿圆柱齿轮是在不改变差动挂轮传动比绝对值大小的情况下在同一台设备上加工,即使加工后的螺旋角有误差,也能保证其正确啮合。
齿轮基本计算公式

齿轮计算公式节圆柱上的螺旋角:L d /tan 00⋅=πβ 基圆柱上的螺旋角:n g αββcos sin sin 0⋅= 齿厚中心车角:Z θ/90︒= 销子直径:m 728.1dp ⋅=中心距离增加系数:)1cos /(cos )2/)((y b 021-⋅+=ααZ Z标准正齿轮的计算(小齿轮①,大齿轮②)1. 齿轮齿 标准 2. 工齿齿形 直齿 3. 模数 m 4. 压力角 c αα=0 5. 齿数 21,Z Z6. 有效齿深 m 2h e ⋅=7. 全齿深 c m h +=28. 齿顶隙 m 35.0,m 25.0,m 2.0c ⋅⋅⋅=9. 基础节圆直径 m d 0⋅=Z 10. 外径 m )2(d k ⋅+=Z 11. 齿底直径 c 2m )2(d r ⋅-⋅-=Z12. 基础圆直径 0g cos m d αZ ⋅⋅= 13. 周节 m t 0⋅=π 14. 法线节距 0e cos m t απ⋅⋅= 15. 圆弧齿厚2/m S 0⋅=π16. 弦齿厚)2sin(m S 1j Z πZ ⋅⋅⋅= 17. 齿轮油标尺齿高 m m h j +Z⋅-⨯⋅Z =)2cos1()2/(π18. 跨齿数5.0)180/(0m ⨯⋅=Z αZ19. 跨齿厚 ])5.0([cos 0o m inva m m S Z ⨯-⋅Z ⋅⋅=πα20. 销子直径 m 728.1d ⋅=21. 圆柱测量尺寸 d m d m +⋅Z =)cos /cos (0φα (偶数齿)d )]90(cos)cos /cos m [(d 0m +︒⨯⋅=ZφαZ (奇数齿)其中, 00)2cos (1απαφinv m d inv +-⋅Z 22. 齿隙f ?移位正齿轮计算公式(小齿轮①,大齿轮②)1. 齿轮齿形 转位 2. 工具齿形 直齿 3. 模数 m 4. 压力角 c αα=05. 齿数 Z6. 有效齿深 m 2h e ⋅=7. 全齿深 c m )]x x (y 2[h 21+⋅⋅-+= 或 c m 2h +⋅=8. 齿隙 c 9. 转位系数 x10. 中心距离 m y x ⋅+=αα11. 基准节圆直径m d 0⋅=Z12. 啮合压力角021210b inv )x x (tan 2inv αZ Z αα+++⋅=13. 啮合节圆直径)(x 2d 211b Z Z Z α+⋅⋅=14. 外径 m )x y (2m )2(d 21k ⋅-⋅+⋅+=Z15. 齿顶圆直径 h 2d d 1k r ⋅-=16. 基圆直径 0cos t g m d α⋅⋅Z = 17. 周节 m t 0⋅=π 18. 法线节距00cos m t απ⋅⋅=19. 圆弧齿厚 010tan m x 22mS απ⋅⋅⋅⋅⋅=20. 弦齿厚)tan x 2x 2sin(m S 1111j Z απZ ⋅⋅+⋅⋅⋅=21. 齿轮游标尺齿高2d d )]tan x 22cos(1[2mh 110k10111j -+⋅⋅+⋅-⋅⋅=Z αZ πZ 22. 跨齿数 5.0180x 1b m 1+⋅=αZ23. 跨齿厚 01m sin m x 2)(S 1α⋅⋅⋅+=标准齿轮的齿厚 24. 梢子直径m 728.1d 1⋅=25. 圆柱测量尺寸11cos cos 1d m d m +⋅⋅Z =φα (偶数齿)1110)90cos(cos cos 1d m d m +Z ︒⋅⋅⋅Z =φα (奇数齿)1010101i 1tan x 2)inv 2(cos m d inv Z ααZ παZ Φ⋅⋅+-⋅-⋅⋅=标准螺旋齿的计算公式(齿直角方式)(小齿轮①,大齿轮②)1. 齿轮齿形 标准2. 齿形基准断面 齿直角3. 工具齿形 螺旋齿4. 模数 n c m m =5. 压力角 n 0c ααα==6. 齿数 1Z7. 螺旋角方向 0β(左或右)8. 有效齿深 n e m 2h ⋅=9.全齿深c m 2h n +⋅=10. 正面压力角n1s cos m tan βZ α⋅=11. 中心距离n21cos 2m )(βZ Z α⋅⋅+=12. 基准节圆直径n10cos m d βZ ⋅=13. 外径 n 01k m 2d d ⋅+= 14. 齿底圆直径 )c m (2d d n 01r ++= 15. 基圆直径gnn 1g cos cos m d 1βαZ ⋅⋅=16. 基圆上的螺旋角 n 0g cos sin sin αββ⋅= 17. 导程1001cot d L 1βπ⋅⋅=18. 周节(齿直角)n n 0m t ⋅=π19. 法线节距(齿直角) n n en cos m t απ⋅⋅= 20. 圆弧齿厚(齿直角) 2m S nn 0⋅=π21. 相当正齿轮齿数101cos βZ Z =22. 弦齿厚)2sin(m S 1v n 1v j 1Z πZ ⋅⋅⋅=23. 齿轮游标尺齿深n 1v n1v 1j m )2cos 1(2m h +⋅-⋅⋅=Z πZ24. 跨齿数 5.01801v n m 1+⋅=Z αZ25. 跨齿厚]inv )5.0m ([cos m S s 11n n m 1αZ Z πα⋅+-⋅⋅⋅=26. 梢子直径)2(cos 1111n v n v n inv inv m d απφα-Z ⋅+⋅Z ⋅=其中,)(2tan 11Rad inv n v n απαφ-Z ⋅+=27. 圆柱测量尺寸11cos cos 1d m d m +⋅⋅Z =φα (偶数齿)1110)90cos(cos cos 1d m d m +Z ︒⋅⋅⋅Z =φα (奇数齿)10101011tan 2)2(cos Z ⋅⋅+-Z ⋅-⋅⋅Z =ααπαφx inv m d inv i 28. 齿隙f移位螺旋齿的计算公式(齿直角方式)(小齿轮①,大齿轮②)1. 齿轮齿形 移位2. 齿形基准断面 齿直角3. 工具齿形 螺旋齿4. 模数(齿直角) n c m m =5. 压力角(齿直角) 0a a a c n -=6. 齿数 1Z7. 螺旋方向 0β8. 有效齿深 n e m h 2= 9. 全齿深 c m h n +=2 10. 移位系数 1n x11. 中心距离n x ym a a +=12. 正面模数0cos βns m m =13. 正面压力角0cos tan βans m =14. 相当正齿轮齿数311βϑs z z v =15. 齿直角啮齿压力角an v v n n ann a inv z z x x b inv +++=2121t an 216. 基准节圆直径11cos βno m z d =17. 外径n n n nk m x m m z d 101122cos ++=β18. 啮齿节圆直径)(22111z z z a d x b +=19. 基圆直径gnn g a m z d βcos cos 11⋅=20. 基础圆柱上的螺旋角 n o g a cos sin sin ββ=21. 圆弧齿厚 n n n on m a x s ⋅⋅+=)tan 22(1π22. 弦齿厚 )t an 22sin(11111v on v n v j z a x z m z s ⋅+⋅⋅=π23. 齿轮游标尺齿高2)}t an 22cos(1{21111111o k v o n v n v d d z a x z m z hj -+⋅+-⋅=π24. 跨齿数 5.018011+=v n m z ab z25. 跨齿厚111sin 2n n n m a m x s ⋅⋅+=)(标准螺旋齿轮的齿厚 26. 销子直径 近似值=1d27. 圆柱测量尺寸/1111cos cos d a m z d ss m +⋅=φ(偶数齿)/1111190cos cos cos d z a m z d s s m +⋅= φ111111tan 2)2(cos z a x inva z a m z d in n n s n n ⋅+--='πφ 注:齿隙f=m 1.25以下 0.025-0.075m 1.25-2.5 0.05-0.10))*25.2((tan 2)2(cos 22111111m r r L z a x inva z a m z d in n n s n n ---⋅+--='πφ。
斜齿轮齿廓任意圆螺旋角计算公式的推导[参考文档]
![斜齿轮齿廓任意圆螺旋角计算公式的推导[参考文档]](https://img.taocdn.com/s3/m/7084c5272e3f5727a4e9621b.png)
附录(5)斜齿轮齿廓上任意圆螺旋角计算公式的推导周万峰大家知道,所谓斜齿轮的螺旋角是指斜齿轮分度圆上的螺旋角。
而分度圆以上圆的螺旋角都大于分度圆螺旋角,分度圆以下圆的螺旋角都小于分度圆螺旋角。
那么不在分度圆上的螺旋角怎样计算呢?也就是说,斜齿轮齿廓上任意圆的螺旋角的计算方法是怎样的呢?它的计算公式是这样的:ββtg dd tg k k = (1) k β——斜齿轮齿廓上任意圆的螺旋角;k d ——斜齿轮齿廓上任意圆直径;d ——斜齿轮分度圆直径;β——斜齿轮分度圆螺旋角。
教材、手册上从未见过这个公式,而且一般也极少计算这个k β的值。
不过有时为了验算变位斜齿轮的齿宽能否进行公法线长度的测量还必须计算这个值,即用公式(1)计算。
那么公式(1)是怎么来的呢? 笔者认为它应该是这样推导出来的:众所周知,斜齿轮的螺旋角是这样形成的:即圆柱体绕自己的轴线作等速转动,圆柱面上有一动点沿素线作等速直线运动,此动点的轨迹就是圆柱面上的螺旋线。
将圆柱面展开,则螺旋线展成一条斜直线,如图1所示。
圆柱转动一圈,动点沿素线移动的距离叫做导程,用T 表示。
圆柱展开面上的斜直线1AA (或21A A )与轴线或母线(圆柱面上平行轴线的线)的夹角叫做螺旋角,用β表示。
图 1显然由图1知,T R tg 2πβ=(2)由公式(2)知,当导程T 一定时,圆柱半径R 越大,则螺旋角β越大;当圆柱体半径R 一定时,导程T 越大,则螺旋角越小。
图2 是斜齿轮齿顶圆展开图,a β是齿顶圆螺旋角。
图3是斜齿轮分度圆展开图,β是分度圆螺旋角。
对同一个斜齿轮而言,分度圆上的导程,齿顶圆上的导程以及齿面上各点的导程都是相同的;但分度圆直径小于齿顶圆直径,故齿顶圆螺旋角大于分度圆螺旋角。
所以,齿顶圆螺旋角的计算公式为T D tg a πβ=,而分度圆螺旋角计算公式为, d tg πβ=所以βπtg d =T ,将T 代入齿顶圆螺旋角计算式,则ββtg dD tg a = (3) 这就是齿顶圆螺旋角的计算公式。
