高速公路坐标计算
3.3高速公路互通立交匝道中线点位坐标计算(精)

(2)分析
AB段为完整的右偏缓和曲线,由所给已知条件,在AB段上点位坐
标按基本型曲线第一段缓和曲线计算原理计算;
(3)求i点坐标
①计算i点在A-xy坐标系下的坐标
l5 l9 x p l 2 2 4 4 40 R l 3456 R l0 0 l l3 l7 l 11 yp 3 3 5 5 6 Rl 336 R l 42240 R l0 0 0 l K i K A l K K B A 0 R rB
X i X O ( K i K O ) cos 0切 Yi YO ( K i K O ) sin 0切
(4)求K0+150点坐标及切线方位角
X i X O ( K i K O ) cos 0切 1378.214 ( K 0 150 K 0 116 )COS 200 1346.264
利用坐标变换公式求i点在线路坐标系下的坐标
X i X ZH xi cos yi sin Yi YZH xi sin yi cos 360 ZH 切
求i点切线坐标方位角
ZH 切
i切
ZH 切
i
l
i
C
i切
l 180 i 2r2 ( L l )
ZH
2
i
L
D
r2
ቤተ መጻሕፍቲ ባይዱ
(4)求K0+407.650点坐标及切线方位角
①将CD段缓和曲线补充完整
L' r2 l' 61.696875 r1 r2
②求 ZH 的切线方位角
高等级公路中桩边桩坐标计算方法

线路工程测量
14.7 线路逐桩坐标计算
2、坐标反算
根据直线起点和终点的坐标,计算直线的边长和坐 标方位角,称为坐标反算。
AB
arctan
YAB X AB
DAB (XAB )2 (YAB )2
线路工程测量
14.7 线路逐桩坐标计算
三、中桩坐标计算
1、直线上点的坐标计算
xp xJDi1 DK p DK JDi1 cosi1,i y p yJDi1 DK p DK JDi1 sin i1,i
(1)第一缓和曲线及圆曲线上点的坐标计算 当P点位于第一缓和曲线(ZH-HY)上,按切线支距法 公式:
xP
l
l5 40R 2l02
JDi
yP
l3 6 Rl0
JDi1
HY ZH
YH HZ
JDi1
线路工程测量
14.7 线路逐桩坐标计算
由坐标转换公式,P点在线路坐标下坐标:
X P X ZH xP cosi1,i KyP sin i1,i YP YZH xP sin i1,i KyP cosi1,i
曲线右偏时K=1;曲线左偏时K=-1;
JDi
JDi1
HY ZH
YH HZ
JDi1
线路工程测量
14.7 线路逐桩坐标计算
(2)圆曲线上点的坐标计算 当P点位于HY-YH圆曲线上,则:
xP m R sin
yP R P R cos
0
DK P
DK HY
R
1800
JDi
HY ZH
JD
YH HZ
线路工程测量
14.7 线路逐桩坐标计算
§14.7 线路中桩、边桩坐标计算
一、引言
高速MC公路测量CASIO4800&4850万能坐标计算程序(完整版)

高速公路测量CASIO4800&4850万能坐标计算程序(完整版)程序特点:真正的全线贯通坐标正反计算、任意斜角计算!!!程序中加入测站点,真正的实现了“坐标法”与“极坐标法”两种放样方法的同时显示的功能,使得放样操作方法选择时更加灵活!!!在曲线元要素输入时仅需要输入第一段全部曲线元要素,后面曲线元要素除起点半径、终点半径、曲线长、转向需输入外其他要素均从前一曲线按辛普森8等分计算得出,解决了主线坐标计算无法获得第二段及其以后曲线元起点参数的问题;辛普森公式任意等分,满足所有精度要求;全线曲线元数据一次性程序化输入,参数存储采用扩充变量数据库,无需修改程序内容;多功能采用单程序编程,避免频繁调用子程序,提高运算速度。
一、程序:ZBJSW“1.ZS 2.FS 3.SZ”:W=1=>Z[2]=0:V=0:Goto 1 ΔW=2=> Goto 4ΔW=3=> O “KOU LING”:O≠123456=>O=0: “OUT”◢Goto CΔO=0: V=0:Z[1]=0:Goto 0←┘Lbi 0←┘”N0.”:Z[1]+1 ◢Z[1]=0=>{ABCREFGUKO}:A“X0”:B“Y0”:C“F0”:R“R0”:E“RN”:F“D0”:G “LS”:U“G”:K“X(00)”: O“Y(00)”: Z[Z[1]×8+3]=A:Z[Z[1]×8+4]=B:Z[Z[1]×8+5]=C:Z[Z[1]×8+6]= R-1:Z[Z[1]×8+7]= E-1:Z[Z[1]×8+8]=F: Z[Z[1]×8+9]=F+G: Z[Z[1]×8+10]=U:“NEXT”◢Isz Z[1]: Goto 0ΔZ[1]=1=>D=Z[9]:Z=0:Z[2]=0:GOTO 2ΔD=Z[(Z[1]-1)×8+9]:Z=0:Z[2]=Z[1]-1:GOTO 2←┘Lbi A←┘Z[Z[1]×8+3]=X:Z[Z[1]×8+4]=Y:Z[Z[1]×8+5]=J: Z[Z[1]×8+8]=D: {REGU}:R“R0”:E “RN”: G“LS”:U“G”: Z[Z[1]×8+6]=R-1:Z[Z[1]×8+7]=E-1: Z[Z[1]×8+9]=D+G: Z[Z[1]×8+10]=U:“NEXT”◢Isz Z[1]: Goto 0←┘Lbi 1←┘{DZT }:D:Z:T“RJ”:Z[2]=0:Goto 2←┘Lbi 2←┘V≠1=>Z[2]>Z[1] =>GoToCΔΔD≤Z[Z[2]×8+9]=> A=Z[Z[2]×8+3]:B=Z[Z[2]×8+4]: C =Z[Z[2]×8+5]:R=Z[Z[2]×8+6]: E=Z[Z[2]×8+7]: F=Z[Z[2]×8+8]: G=Z[Z[2]×8+9]: U=Z[Z[2]×8+10]: Goto3ΔIsz Z[2]:Goto 2←┘Lbi 3←┘W=3 =>N=8:≠P=U(E-R)÷Abs(G-F):Q=Abs(D-F)÷N:S=90Q÷π:J=C+(NPQ+2UR)NS:L=1←┘X=A+Q÷6×(Cos C+Cos J +4∑(Cos (C+((L+0.5)PQ+2UR)×(L+0.5)S),L,0,(N-1))+2∑(Cos (C+((LPQ+2UR)LS,L,1,(N-1)))+ZCos(J+ T)←┘Y=B+Q÷6×(Sin C+Sin J +4∑(Sin (C+((L+0.5)PQ+2UR)×(L+0.5)S),L,0,(N-1))+2∑(Sin (C+((LPQ+2UR)LS,L,1,(N-1)))+Z Sin(J+T):V=1=>Goto6ΔV=2=>Goto9ΔV=3=> GOTO CΔW=3=>GOTO AΔZ=0=>“X(Z)=”:X:Pause 0: “Y(Z)=”:Y◢Pol((X-K),(Y-O))←┘“S(Z)=”:I ◢J<0=> J=J+360Δ“F(Z)=”: J→DMS◢Goto 1ΔZ<0=>“X(L)=”:X:Pause 0: “Y(L)=”:Y◢Pol((X-K),(Y-O))←┘fx4850①“S(L)=”:I ◢J<0=> J=J+360Δ“F(L)=”: J→DMS◢Goto 1ΔZ>0=>“X(R)=”:X:Pause 0: “Y(R)=”:Y ◢Pol((X-K),(Y-O))←┘“S(R)=”:J ◢J<0=> J=J+360Δ“F(R)=”: J→DMS◢Goto 1 ←┘Z=0=> X “X(Z)=”◢Y “Y(Z)=”◢Pol((X-K),(Y-O))←┘I“S(Z)=”◢J<0=> J=J+360ΔJ“F(Z)=”◢Goto 1ΔZ<0=> X “X(L)=”◢Y “Y(L)”◢Pol((X-K),(Y-O))←┘fx4800②I“S(L)=”◢J<0=> J=J+360ΔJ“F(L)=”◢Goto 1ΔZ>0=> X “X(R)=”◢Y “Y(R)=”◢Pol((X-K),(Y-O))←┘I“S(R)=”◢J<0=> J=J+360ΔJ“F(R)=”◢Goto 1 ←┘Lbi 4←┘{MH} :M“X”:H“Y”:Z[2]=0:GOTO 5←┘Lbi 5←┘V=1:D= Z[Z[2]×8+9]:Z=0:T=90:GOTO 2←┘Lbi 6←┘K=((H -B)Cos(C-90)-(M-A)Sin(C-90))×((H -Y)Cos(J-90)-(M-X)Sin(J-90)):K≤0=> Goto 7ΔIsz Z[2]:Goto5←┘Lbi 7←┘D=F+Abs((H -B)Cos(C-90)-(M-A)Sin(C-90)):D>G=> Isz Z[2]: Goto5ΔGoto 8←┘Lbi 8←┘V=2 :GOTO 3←┘Lbi 9 ←┘K=(H -Y)Cos(J-90)-(M-X)Sin(J-90):Abs K<(1÷E)^3=>Goto BΔD=D+K :GOTO 8←┘Lbi B←┘V=3 :Z=0:Goto 3←┘Lbi C←┘Z=(H-Y) ÷Sin(J+90):“D”:D:Pause 0: “Z”: Z◢4850输出(Z=(H-Y) ÷Sin(J+90):D“D”◢Z “Z”◢4800输出)GOTO 4←┘Lbi C←┘二、说明a、编制说明本程序是运用复化辛普生公式根据曲线段——直线、圆曲线、缓和曲线(完整或非完整型)的线元要素(起点坐标、起点里程、起点切线方位角、线元长度、起点曲率半径、止点曲率半径)及里程边距,对该曲线段范围内任意里程中边桩坐标进行计算,以及对卡西欧扩充变量的灵活应用,实现了真正意义上的的全线贯通及曲线要素输入程序化(在不修改程序内容的情况下可通过运行程序输入任意多段曲线元要素)。
缓和曲线)计算公式
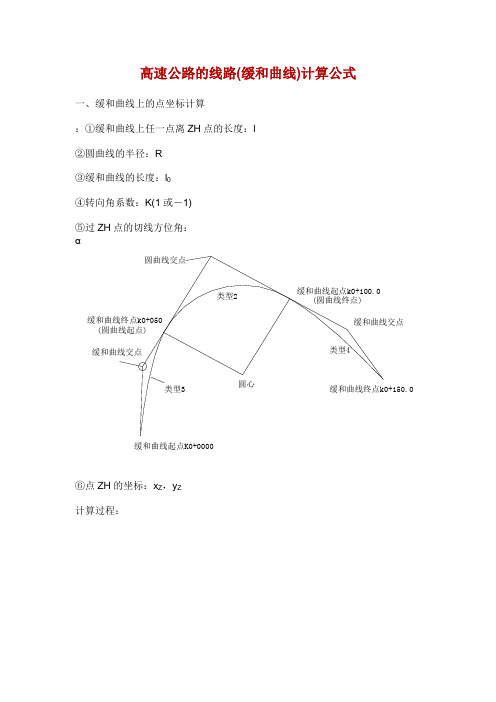
高速公路的线路(缓和曲线)计算公式一、缓和曲线上的点坐标计算:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,那么:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,那么:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度〔或缓曲上任意点到缓曲起点的长度〕l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算:①第一坡度:i1(上坡为“+〞,下坡为“-〞)②第二坡度:i2(上坡为“+〞,下坡为“-〞)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程五、超高缓和过渡段的横坡计算:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点〔过渡段终点〕的间隔:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-〞,右转为“+〞)⑦曲线终点处曲率:P1(左转为“-〞,右转为“+〞)求:①线路匝道上点的坐标:x,y ②待求点的切线方位角:αT计算过程:。
怎样计算高速公路路线坐标及高程

一个excle模板的制作在当今社会,excle的使用已经是越来越来频繁了,几乎涉及所有的行业,路桥施工也不例外。
我在某路桥公司曾经负责过某项目部的测量工作。
大家都知道,测量最主要的就是计算了,如坐标、高程、横坡度等。
我现在给大家推荐一款我自己编制的关于测量计算的excel模板.首先我会跟大家介绍一下模板的作用,然后再一一讲解此模板的制作过程.首先给大家看一下此模板的界面如下:也许大家咋一看,切~ 这算啥,我也会做这张表格,实在是太简单了.不错,如果仅仅是靠手动输入这样子的数字,也许只要懂一点点excle的人都会制作出这张表格吧。
不过,这张表格并不是你表面所看到的仅仅是几个数字而已,其内在的公式才是它的亮点。
也许这样讲大家还不是很清楚,我继续给大家截个图,看看它里面的公式是什么。
大家注意到上面的公式了吗,并不是仅仅是输入数字就完事的,它是一个自定义函数zb x(),那么后面的都是一样吗?完全正确,后面的都是自定义函数,它们分别是zby()、sqx()、hpz()、hpy()。
也许大家会问,恩,是不错,但是有什么用呢?那让我先给大家简述一下这个自定义函数的用法。
竟然是一个函数,那么它就必须要有一个自变量,这几个函数的自变量又是什么呢?其实这个模板里面所有函数的自变量只有一个,就是桩号。
什么意思?就是只要你给出任意一个桩号,都能得到其对应的坐标、中桩高程和横坡度.假设我们要K38+000~K38+200段落内每隔20M一个断面所有点的坐标、中桩高程、以及左右横坡。
我就用这个模板给大家演示一下(此模板暂时数据只针对黄祁高速公路六标项目部)。
先在桩号那一列把K38+000~K38+200输入进去,可不要真的把字母“K”和加号“+”给输进去,只用输入纯数字就行了,否则计算会出错,之所以在模板里显示的是那样子,只不过是自定义的单元格式而已。
第二步剩下的仅仅就是拖动公式了,后面的都是公式,所以可以一起拖下来,先选定后面的所有单元格,然后向下直接拖动至最后,那么你需要的数据就全部出来了。
道路曲线高程计算公式

高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道) 一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:。
高速公路的一些线路坐标
高速公路的一些线路坐标、高程计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l 2——第二缓和曲线长度l——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1、第二横坡:i2、过渡段长度:L、待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K③曲线终点桩号:K1④曲线起点坐标:x0,y⑤曲线起点切线方位角:α⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
坐标法计算高速公路边桩坐标
取负号 ; 当曲线右转时, 取正号。 横断面的坐标方位角即可从横断面的切线坐标 方位角求得 , 公式如下 : 横 面= 断 切± 0 9。
() 4
为了计算边桩的坐标 , 先假定一个坐标系 , 以 是 高程 、 距离 作为 横纵 坐标 的系 统 。这 样计 算 出来 的
数值 , 在道 路施工 中使 用 还不 能 达到 与 国家 坐 标 系 统 的统一 。因此需 将 假定 坐 标数 值 , 化到 国家 坐 转
切= 终 起 切士
2 1 00
() 3
x 一在 xy o 坐标系下 , 两坡线的交点高程值 ;
y 一在 xy坐标 系下 , o 两坡线 的交 点距 离道 路 中 桩 的水平 距离 。 23 在 国家坐标 系下边桩 坐标的计 算 .
其 中: :
J、 T 1
公 式 中“±” 的判 断 方 法 是 , 圆 曲 线左 转 时 , 当
2 2 在假 定 坐标 系下 边桩 坐标 的计 算公 式 .
边桩 坐 标 的计算 公 式 , 先 简化 为 求解 已知斜 首
率两条直线的交点坐标。由于直线的斜率计算公式 与道 路坡 度的计算 公式相 同 , 因而 , 将斜 率置换 为坡
度, 即为边 桩坐标 计算公 式 的推导原 则 。
要 : 出坐标 法计算边桩 坐标 , 提 将微分思路 引入 到边桩 坐标 值的计算 , 通过观测 数据和计 算公式 , 直接得
出边桩 坐标 值 。 坐标 法是 对 传 统 边 桩 放 样 方 法的 很 好 的 补 充 。
关 键 词 : 家统 一 坐 标 系统 ; 桩 ; 国 边 高速 公路
道 路 边桩 的放 样 方 法 主要集 中在 逐渐 趋 近法 , 即费 时又费力 。本 文所提 出 的坐 标法 就是 利用 图纸 或实测 数据 , 计算 出边桩 的坐标 , 先 进行 边桩 放样 的 方法 。此方法 与逐渐趋 近法 相 比 , 工作 强度 降低 , 施 工 精度 提高 。利 用 坐标 法 进 行边 桩放 样 时 , 如果 道 路各 中桩点 有准 确 的横 断 面数 据 , 不 进 行外 业 观 可 测 。因此对 于坐标 法 的应 用 , 只要 获 取 到 横 断 面 的 数据 , 即可根据 路基 的结 构 图直 接 计 算 出边 桩 的坐
高速公路的一些线路坐标、高程计算公式
高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
高速公路缓和曲线中桩坐标计算方法
高速公路缓和曲线中桩坐标计算摘要:本文讲解了在利用全站仪进行缓和曲线中桩放样时,缓和曲线的基本形和卵形两种情况下中桩坐标计算的方法。
关键词:缓和曲线,基本形,卵形,中桩坐标计算随着全站仪在道路工程施工测量中的普及,传统的中线放样方法逐渐被淘汰。
目前道路工程中线放样时,只要能计算出中线上任意一点的坐标,用全站仪或者GPS RTK的坐标放样功能就可很方便、快捷地完成实地放样。
道路线形是由直线、圆曲线、缓和曲线三种线形组合而成的,而直线与圆曲线组合的线形(见图一)中桩坐标计算比较简单,在此不作阐述。
下面就缓和曲线与其它两种线形组合的线形中桩坐标计算予以分析。
缓和曲线与其它两种线形组合构成的线形主要有缓和曲线的完整形(即基本形)(见图二)和非完整形(即卵形)(见图三)二种。
一、基本形曲线中桩坐标计算:1、对于第一缓和曲线及圆曲线段(ZH~YH)(如图四),建立以ZH为坐标原点,切线方向为X′轴,半径方向为Y′轴的曲线坐标系(X′O′Y′)。
先计算曲线各点在曲线坐标系下的坐标。
⑴对于第一缓和曲线段(ZH~HY)内任一点i(此时L=K i-K ZH)若圆曲线半径R≥100m时,则X i′=L-L5/(40R2L s12) 公式①Y i′=L3/(6RL s1) 公式②若圆曲线半径R<100m时,则X′=L-L5÷[40(RL S)2]+L9÷[3456(RL S)4]–L13÷[599040(RL S)6]+L17÷[175472640(RL S)8]- L21÷[7.80337152×1010(RL10](公式③)S)Y′=L3÷[6(RL S)] - L7÷[336(RL S)3]+L11÷[42240(RL S)5] - L15÷[9676800(RL S)7]+L19÷[3530096640(RL S)9] - L23÷[1.8802409472×1012(RL S)11](公式④)⑵对于圆曲线段(HY~YH)上任一点iX i′=q+Rsin¢iY i′=R(1-cos¢i)+pL=K i-K ZH¢i=(L- L s1)*180/(Rπ)+β0内移值P=L s12/(24R)切线增值q= L s1/2- L s13/(240R2)综合⑴、⑵,根据不同坐标系的相互转换,可得ZH~YH上任一点i的中桩测量坐标为:X i=X ZH+cosA×X i′-sinA×f×Y i′(公式⑤)Y i= Y ZH+sinA×X i′+cosA×f×Y i′(公式⑥)式中f为线路的转向系数,右转时f=1,左转时f=-1 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高速公路的一些线路计算
一、缓和曲线上的点坐标计算
已知:①缓和曲线上任一点离ZH 点的长度:l
②圆曲线的半径:R ③缓和曲线的长度:l 0 ④转向角系数:K(1或-1) ⑤过ZH 点的切线方位角:α ⑥点ZH 的坐标:x Z ,y Z 计算过程:
y y ⑼y x x ⑻x αSsin y ⑺αScos x ⑹90ααα⑸y x ⑷S 180
n x y
arctg α⑶l 3456R l l 40R l l y ⑵)K
R
336l l 6Rl l (x ⑴Z
1Z
11111012
200
0040
49202503307
030+=+===-+=+=⋅+=+-=-=
说明:当曲线为左转向时,K=1,为右转向时,K=-1,
公式中n 的取值如下:
⎪⎩
⎪⎨⎧=<<⎪⎩⎪⎨⎧=><⎪⎩⎪⎨⎧=<>⎪⎩⎪⎨⎧=>>1n 0y 0x 1n 0y 0x 2n 0y 0x 0n 0y 0x 00000000 当计算第二缓和曲线上的点坐标时,则: l 为到点HZ 的长度
α为过点HZ 的切线方位角再加上180° K 值与计算第一缓和曲线时相反 x Z ,y Z 为点HZ 的坐标
切线角计算公式:2Rl l β02
=
二、圆曲线上的点坐标计算
已知:①圆曲线上任一点离ZH 点的长度:l
②圆曲线的半径:R ③缓和曲线的长度:l 0 ④转向角系数:K(1或-1) ⑤过ZH 点的切线方位角:α ⑥点ZH 的坐标:x Z ,y Z 计算过程:
y y ⑿y x x ⑾x αSsin y ⑽αScos x ⑼90ααα⑻y x ⑺S 180n x y arctg
α⑹m Rsin α'y ⑸p]K )cos α'[R(1x ⑷34560R l 240R l 2l ⑶m 2688R l 24R l ⑵p R π)
l -90(2l ⑴α'Z
1Z
11111012
200
0004
5
2
3003
40
200+=+===-+=+=⋅+=+=+-=+-=-
==
说明:当曲线为左转向时,K=1,为右转向时,K=-1,
公式中n 的取值如下:
⎪⎩
⎪⎨⎧=<<⎪⎩⎪⎨⎧=><⎪⎩⎪⎨⎧=<>⎪⎩⎪⎨⎧=>>1n 0y 0x 1n 0y 0x 2n 0y 0x 0n 0y 0x 00000000 当只知道HZ 点的坐标时,则: l 为到点HZ 的长度
α为过点HZ 的切线方位角再加上180° K 值与知道ZH 点坐标时相反 x Z ,y Z 为点HZ 的坐标
三、曲线要素计算公式
β
+∆=+=+=+-=++=++++-=
++++-=-=
-=
+-
=+-==
=
+=+==
D l l :β
R R R
2R P P 2β⒀曲线段长度:l )
l l (21
R αL ⑿圆曲线长度)
l l (21
R α⑾曲线全长度:L m 2α
2R)tg p p (212α2tg
p p T ⑽第二切线长:m 2α
2R)tg p p (212α2tg
p p T ⑼第一切线长:2688R l 24R l p ⑻第二曲线平移量:2688R l 24R l p ⑺第一曲线平移量:34560R l 240R l 2l m ⑹第二曲线顺移量:34560R l 240R l 2l m ⑸第一曲线顺移量:2R
l β:⑷第二缓曲段总转角值2R l β:⑶第一缓曲段总转角值)l
P P (21l R R 2R
R :β⑵曲线段任意点转角值2Rl l :β⑴缓曲段任意点转角值2
1212121021221212121121
34
222
23
41
2114
52232224
512311
12
21
12121210
2
的边缘曲线长度⒁偏离缓曲:D 公式中各符号说明:
l ——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度) l 1——第一缓和曲线长度 l 2——第二缓和曲线长度 l 0——对应的缓和曲线长度 R ——圆曲线半径 R 1——曲线起点处的半径 R 2——曲线终点处的半径 P 1——曲线起点处的曲率 P 2——曲线终点处的曲率 α——曲线转角值
四、竖曲线上高程计算
已知:①第一坡度:i 1(上坡为“+”,下坡为“-”)
②第二坡度:i 2(上坡为“+”,下坡为“-”) ③变坡点桩号:S Z ④变坡点高程:H Z ⑤竖曲线的切线长度:T ⑥待求点桩号:S
计算过程:
)i i T(4
12R T E ⑷i Ri 2
12R )i i R(21l H ⑶H i i 2T
⑵R (带有符号)S S l ⑴122
02
1212
Z 1
2Z -==-⎥⎦⎤⎢⎣⎡+++=-=
-=
五、超高缓和过渡段的横坡计算
已知:如图,
第一横坡:i
1
第二横坡:i
2
过渡段长度:L
待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i
解:d=x/L
i=(i
2-i
1
)(1-3d2+2d3)+i
1
六、匝道坐标计算 已知:①待求点桩号:K
②曲线起点桩号:K 0 ③曲线终点桩号:K 1 ④曲线起点坐标:x 0,y 0 ⑤曲线起点切线方位角:α0
⑥曲线起点处曲率:P 0(左转为“-”,右转为“+”) ⑦曲线终点处曲率:P 1(左转为“-”,右转为“+”) 求:①线路匝道上点的坐标:x,y
②待求点的切线方位角:αT 计算过程:
ααα Bcos NAsinT y y BsinT
NAcosT x x 42240C
l l 336C l l 6C l l B 3456C l l 40C l l )l (l A /2C l N αT )/2/C l S(l α P P l C SN l l )P /(P P Nl l K K l )P SGN(P N 时:P P ⑶当αα )/P cos α(cos αy y )/P sin α(sin αx x αSP α 0时:P P ⑵当αα Ssin αy y Scos αx x 0时:P P ⑴当K -K S 1
0T 005
110
1137073034
90
9
25050200010
1S 0010S 00
1S 01101T 101010100
11100T 0000100
+=++=-+=-+---=-+---=-=+=-=
+=-=-=-=≠=--=-+=+=≠==+=+====
T。
