暑期高一升高二数学试卷
2020年暑期数学衔接教材高一升高二(共39页)无答案

圆锥曲线()()⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧⎩⎨⎧⎩⎨⎧⎩⎨⎧利用图形的特点②图形思想利用方程的特点①方程思想数形思想②抛物线的性质①抛物线的定义抛物线②双曲线的性质①双曲线的定义双曲线②椭圆的性质①椭圆的定义椭圆②求曲线的方程①曲线与方程的关系曲线与方程知识结构 第一节:曲线与方程知识要点(1)曲线与方程数的思想⎩⎨⎧点都在曲线上。
②以方程的解为坐标的是方程的解。
①曲线上的点的坐标都形的思想⎩⎨⎧截距,距离等)②图形的性质(斜率,长①坐标可以表示线段的理解运用①曲线上的点都是方程的解,实际解题中:A 把点代入方程;B 通过解方程组求交点;C 把两条曲线的方程合并为一元二次方程,通过判别式判断两曲线的位置关系;D 用韦达定理进行求解。
②图形的性质就是涉及图形的几何特征。
例、过点且与曲线相交所得弦长为的直线方程为 。
1,已知曲线C 的方程是)0(022<=+-+m my mx y x ,下列各点不可能在曲线C 上的点是( )A .)0,0(B .)2,0(mC .)2,0(m -D .)0,2(m2,直线23+=x y 被曲线221x y =所截得的线段的中点到原点的距离是( ) A .229 B .429 C .29 D .293、若直线x +my =2+m 与圆x 2+y 2—2x —2y +1= 0相交,则实数m 的取值范围 是4,已知直线:40l x y -+=与圆()()22:112C x y -+-=,则C 上各点到l 的距离的最小值为_______.5,点(3,1)和点(6,4-)在直线023=+-a y x 的两侧, 则a 的取值范围是 。
6.下列方程的曲线关于直线x y =对称的是( )A .122=+-y x xB .122=+xy y xC .1=-y xD .122=-y x第二节:求曲线方程1,求曲线方程主要有三种方法:(1)直译法(2)坐标代入法(3)参数法(4)交轨法求曲线方程的五个步骤:(1)建立适当的直角坐标系,用(x,y)表示曲线上任意一点M的坐标;建标(2)写出适合条件P的点M的集合P={M|P(M)};设点(3)用坐标表示条件P(M),列出方程f(x,y)=0 列式(4)化方程f(x,y)=0为最简方程化简(5)证明以化简后的方程的解为坐标的点都是这条曲线上的点.除个别情况外,化简过程都是同解变形过程,步骤(5)可以不写,也可以省略步骤(2),直接列出曲线方程.例、已知圆A:(x+2)2+y2=1与点A(-2,0),B(2,0),分别求出满足下列条件的动点P的轨迹方程.(1)△PAB的周长为10;(2)圆P与圆A外切,且点B在动圆P上(P为动圆圆心);(3)圆P与圆A外切且与直线x=1相切(P为动圆圆心).学以致用1,求点P (4,-2)与圆224x y +=上任一点连线的中点轨迹方程?2.已知动点M 到定点)0,9(A 的距离是M 到定点)0,1(B 的距离的3倍, 求M 的轨迹方程?3、在直角△ABC 中,斜边是定长2a (0)a >,求直角顶点C 的轨迹方程。
高一升高二暑假数学测试题及详细答案

绝密★启用前 高一升高二暑假数学测试题及详细答案一、单选题1.已知集合{}}242{60M x x N x x x =-<<=--<,,则M N ⋂= A .}{43x x -<< B .}{42x x -<<- C .}{22x x -<< D .}{23x x << 2.已知函数23x y a -=+(0a >且1a ≠)的图像恒过定点P ,点P 在幂函数()y f x =的图像上,则3log (3)f =( )A .2-B .1-C .1D .23.若a ,b ,c 满足23a =,2log 5b =,32c =.则( )A .c a b <<B .b c a <<C .a b c <<D .c b a << 4.已知函数()22x f x =-,则函数()y f x =的图象可能是( )A .B .C .D .5.已知非零向量a b ,满足2a b =,且b a b ⊥(–),则a 与b 的夹角为A .π6B .π3C .2π3D .5π6 6.已知a =tan(−π5),b =tan(7π5),c =sin(−π5)则有( )A .a >b >cB .c >b >aC .c >a >bD .b >c >a7.若向量a=1,22⎛- ⎝⎭,|b |=a ·(b -a )=2,则向量a 与b 的夹角( ) A .6π B .4π C .3π D .2π 8.一个几何体按比例绘制的三视图如图所示(单位:m ),则该几何体的体积为A .73m 3B .92m 3C .94m 3D .72m 3 9.下列命题错误的是( )A .不在同一直线上的三点确定一个平面B .两两相交且不共点的三条直线确定一个平面C .如果两个平面垂直,那么其中一个平面内的直线一定垂直于另一个平面D .如果两个平面平行,那么其中一个平面内的直线一定平行于另一个平面10.若,,a b c ∈R ,则下列结论正确的是( )A .若a b >,则22ac bc >B .若a b <,则11a b >C .若,a b c d >>,则ac bd >D .若a b >,则a c b c ->-二、解答题11.已知1x ,2x 是方程240x mx -+=的两个根,且()1212lg 2lg lg x x x x +=+,求m 的值. 12.已知集合{}|1A x x =≥,集合{}|33,B x a x a a R =-≤≤+∈.(1)当4a =时,求A B ;(2)若B A ⊆,求实数a 的取值范围.13.已知向量(1,2)a =,(3,4)b =-.(1)求3a b -的值;(2)若()a a b λ⊥+,求λ的值.14.如图,四棱锥P ABCD -的底面是边长为2的菱形,PD ⊥底面ABCD .(1)求证:AC ⊥平面PBD ;(2)若2PD =,直线PB 与平面ABCD 所成的角为45,求四棱锥P ABCD -的体积. 15.已知数列{}n a 是公差不为零的等差数列,1a =1,且139,,a a a 成等比数列.(1)求数列{}n a 的通项;(2)设2n an b =,求数列{}n b 的前n 项和S n . 16.在数列{}n a 中,112a =,点()1()*n n a a n N +∈, 在直线12y x =+上 (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)记n 11n n b a a +=⋅ ,求数列{}n b 的前n 项和n T . 三、填空题(任选5题)17.已知函数(32)4,1,()log ,1,aa x a x f x x x -+<⎧=⎨≥⎩对任意不相等的实数1x ,2x ,都有1212()()0f x f x x x -<-,则a 的取值范围为__________.18.已知函数()()()21,02,0x x f x x x ⎧+≤⎪=⎨->⎪⎩,则()1f f =⎡⎤⎣⎦__________ 19.已知函数()f x 是奇函数,当0x >时,()lg f x x =,则1100f f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭的值为 ______ 20.若1cos 3α=,则sin()2πα-=________. 21.已知1,22cos cos sin sin αβαβ+=+=则() cos αβ-= ________. 22.已知等差数列{}n a 的前n 项和为n S ,且746a a -=,7451S S -=-,则n a =______.23.设x ,y 满足约束条件2030240x y x y -⎧⎪+≥⎨⎪+-≤⎩,则2z x y =+的最小值是___________.详细参考答案1.C【分析】本题考查集合的交集和一元二次不等式的解法,渗透了数学运算素养.采取数轴法,利用数形结合的思想解题. 【详解】 由题意得,{}{}42,23M x x N x x =-<<=-<<,则 {}22M N x x ⋂=-<<.故选C .【点睛】不能领会交集的含义易致误,区分交集与并集的不同,交集取公共部分,并集包括二者部分. 2.D【分析】根据指数函数的图象与性质,求出定点P 的坐标,再利用待定系数法求出幂函数()f x ,从而求出3log (3)f 的值.【详解】解:函数23x y a -=+中,令20x -=,解得2x =,此时134y =+=,所以定点(2,4)P ;设幂函数()a y f x x ,则24a =,解得2a =;所以2()f x x =,所以()()2339f ==, ()333log l 9og 2f ∴==.故选D .【点睛】本题考查用待定系数法求幂函数解析式,以及指数函数的性质,是基础题.3.A【分析】利用指数函数和对数函数的单调性即可比较大小.【详解】23a =,12232<<,∴12a <<,22log 5log 4b =>,∴2b >,32c =,01323<<,∴01c <<,∴c a b <<,故选:A.【点睛】本题考查了指数函数和对数函数的单调性,考查了计算能力和推理能力,属于基础题. 4.B【分析】先将函数化成分段函数的形式,再根据函数在不同范围上的性质可得正确的选项.【详解】 因为()22xf x =-,故22,1()22,1x x x f x x ⎧-≥=⎨-<⎩, 所以在[)1,+∞内,()f x 为增函数;在(),1-∞内,()f x 为减函数.排除ACD,故选:B.【点睛】本题考查函数图象的识别,此类问题一般根据函数的奇偶性、单调性、函数在特殊点处的函数的符号等来判别,本题属于基础题.5.B【分析】本题主要考查利用平面向量数量积计算向量长度、夹角与垂直问题,渗透了转化与化归、数学计算等数学素养.先由()a b b -⊥得出向量,a b 的数量积与其模的关系,再利用向量夹角公式即可计算出向量夹角.【详解】因为()a b b -⊥,所以2()a b b a b b -⋅=⋅-=0,所以2a b b ⋅=,所以cos θ=22||122||a bb b a b ⋅==⋅,所以a 与b 的夹角为3π,故选B . 【点睛】对向量夹角的计算,先计算出向量的数量积及各个向量的摸,在利用向量夹角公式求出夹角的余弦值,再求出夹角,注意向量夹角范围为[0,]π.6.D【分析】首先通过诱导公式,化简三个数,然后判断它们的正负性,最后利用商比法判断 a,c 的大小,最后选出正确答案.【详解】a =tan(−π5)=−tan π5<0,b =tan(7π5)=tan(π+25π)=tan 25π>0,c =sin(−π5)=−sin π5<0, 而a c =−tan π5−sin π5=1cos π5>1,c =sin(−π5)=−sin π5<0⇒a <c ,故本题选D. 【点睛】本题考查了诱导公式、以及同角三角函数关系,以及商比法判断两数大小.在利用商比法时,要注意分母的正负性.7.A 【分析】根据向量的数量积运算,向量的夹角公式可以求得.【详解】 由已知可得:22a b a -= ,得3a b = ,设向量a 与b 的夹角为θ ,则3cos .2a b a b θ==⨯ 所以向量a 与b 的夹角为6π故选A.【点睛】本题考查向量的数量积运算和夹角公式,属于基础题.8.D【解析】试题分析:由三视图可知:该空间几何体由三个棱长为的正方体,和一个三棱柱组成,所以该几何体的体积为. 考点:三视图.9.C【分析】利用公理和线与面的平行和垂直定理及其推论求解.【详解】由公理知直线及直线外一点,确定一个平面,故A 正确;由公理知两两相交且不共点的三条直线确定一个平面,故B 正确;由面面垂直的性质定理知错误,故C 不正确;由面面平行的性质定理知正确,故D 正确;.故选C .【点睛】本题考查命题真假的判断,是基础题,解题时要认真审题,注意对概念的理解和定理,性质的应用,属于基础题.10.D【分析】根据不等式的基本性质逐一判断可得答案.【详解】解:A .当0c 时,不成立,故A 不正确;B .取1a =-,1b =,则结论不成立,故B 不正确;C .当0c <时,结论不成立,故C 不正确;D .若a b >,则a c b c ->-,故D 正确.故选:D .【点睛】本题主要考查不等式的基本性质,属于基础题.11.16m =【分析】由根与系数关系,先得到12x x m +=,124x x =,再由对数运算,即可求出结果.【详解】由题意可得,12x x m +=,124x x =,2160m ∆=->,即216m >;又()1212lg 2lg lg x x x x +=+,所以()412lg lg log 2lg lg 4m m m x x ===, 因此16m =,满足216m >,故16m =.【点睛】本题主要考查对数的运算,熟记对数运算法则即可,属于基础题型.12.(1)[)1,-+∞(2)(],2-∞【分析】(1)当4a =时,[]1,7B =-,根据并集定义,即可求得A B ;(2)因为B A ⊆,分别讨论B =∅和B ≠∅两种情况,即可求得实数a 的取值范围.【详解】(1)当4a =时,[]1,7B =-∴ 又[)1,A =+∞,则[)1,A B ⋃=-+∞(2)因为{}|1A x x =≥,B A ⊆当B =∅时,33a a ->+,解得0a <当B ≠∅时,3331a a a -≤+⎧⎨-≥⎩,解得02a ≤≤ 综上所述,实数a 的取值范围为(],2-∞.【点睛】本题考查了并集运算和子集运算.本题的解题关键是掌握当B A ⊆时,分别讨论B =∅和B ≠∅两种情况,考查了分析能力和计算能力,属于基础题.13.(1)3210a b -=(2)1λ=-【分析】 (1)根据题中条件,先求出3(6,2)a b -=,进而可求出结果;(2)先由题意得到(13,24)a b λλλ+=-+,根据()a ab λ⊥+得到()0a a b λ⋅+=,进而可求出结果.【详解】(1)因为向量(1,2)a =,(3,4)b =-,则3(6,2)a b -=,则236a b -=+=(2)因为向量(1,2)a =,(3,4)b =-,则(13,24)a b λλλ+=-+,若()a a b λ⊥+,则()1(13)2(24)550a a b λλλλ⋅+=⨯-+⨯+=+=,解得:1λ=-.【点睛】本题主要考查求向量的模,以及根据向量垂直求参数的问题,熟记向量的坐标运算即可,属于常考题型.14.(1)证明见解析;(2 【分析】(1)通过AC ⊥BD 与PD ⊥AC 可得AC ⊥平面PBD ;(2)由题先得出∠PBD 是直线PB 与平面ABCD 所成的角,即∠PBD =45°,则可先求出菱形ABCD 的面积,进而可得四棱锥P - ABCD 的体积.【详解】解:(1)因为四边形ABCD 是菱形,所以AC ⊥BD ,又因为PD ⊥平面ABCD ,AC ⊂平面ABCD ,所以PD ⊥AC ,又PD BD D ⋂=,故AC ⊥平面PBD ;(2)因为PD ⊥平面ABCD ,所以∠PBD 是直线PB 与平面ABCD 所成的角,于是∠PBD =45°,因此BD =PD =2.又AB = AD =2,所以菱形ABCD 的面积为sin 60S AB AD ︒=⋅⋅=故四棱锥P - ABCD 的体积13V S PD =⋅=. 【点睛】本题主要考查空间线、面关系等基础知识,同时考查空间想象能力、推理论证能力以及运算求解能力,是基础题.15.(1)a n =n . (2)S n =2n +1-2.【详解】(1)由题设知公差d ≠0,由a 1=1,a 1,a 3,a 9成等比数列得121d +=1812d d++, 解得d =1,d =0(舍去),故{a n }的通项a n =1+(n -1)×1=n . (2)由(1)知2=2n a n nb =,由等比数列前n 项和公式得S n =2+22+23+…+2n =()21212n --=2n +1-2.点评:掌握等差、等比数列的概念及前n 项和公式是此类问题的关键.16.(Ⅰ)()11(1)*222n n a n n N =+-=∈ (Ⅱ)41n n T n =+ 【分析】(Ⅰ)根据点在直线上,代入后根据等差数列定义即可求得通项公式.(Ⅱ)表示出{}n b 的通项公式,根据裂项法即可求得n T .【详解】 (Ⅰ)由已知得112n n a a +=+,即112n n a a +-= ∴ 数列{}n a 是以12 为首项,以12d =为公差的等差数列 ∵()11n a a n d +-= ∴()()111*222n n a n n N =+-=∈ (Ⅱ)由(Ⅰ)得()141122n b n n n n ==++⨯ ∴1141n b n n ⎛⎫=- ⎪+⎝⎭∴111111141223341n T n n ⎛⎫=-+-+-+⋅⋅⋅- ⎪+⎝⎭ 1411n ⎛⎫=- ⎪+⎝⎭ 41n n =+ 【点睛】本题考查了等差数列定义求通项公式,裂项法求和的应用,属于基础题.17.2273a ≤< 【分析】利用已知条件判断函数的单调性,然后转化分段函数推出不等式组,即可求出a 的范围.【详解】对任意的实数12x x ≠,都有()()12120f x f x x x -<-成立,可得函数为减函数,可得:320013240a a a a -<⎧⎪<<⎨⎪-+⎩, 解得2[7a ∈,2)3. 故答案为:2273a ≤<. 【点睛】本题考查分段函数的应用,函数的单调性以及对数函数的性质的应用,属于基本题. 18.5【分析】把自变量的值根据所在的范围代入解析式,由内向外依次计算。
高一升高二暑假数学(直线方程、圆的方程、椭圆方程)

A. (, )
B. (,1)
C. ( ,1]
D.[1 , )
【3】圆 (x 2)2 y2 5 关于 y 轴对称的圆的方程为 ( )
A. x2 ( y 2)2 5
B. x2 ( y 2)2 5
C. (x 2)2 y2 5
D. (x 2)2 ( y 2)2 5
【4】过点 A (1, 1) 、 B (1,1) 且圆心在直线 x y 2 0 上的圆的方程是 ( )
8
题型 4 对称问题
【1】已知直线 l : 2x 3y 1 0 ,点 A(1, 2) .求: (1)点 A 关于直线 l 的对称点 A 的坐标; (2)直线 m : 3x 2y 6 0 关于直线 l 对称的直线 m 的方程; (3)直线 l 关于点 A(1, 2) 对称的直线 l 的方程.
P x0,
y0 ,且满足
y0
x0
2 ,则
y0 x0
的取值范围为(
)
A.
1 2
,
1 5
B.
,
1 5
C.
1 2
,
1 5
D.
1 2
,0
3
基础知识 2 直线的方程
【1】过点 (1,2) ,且倾斜角为 60 的直线方程是 ( )
A. y 2 3(x 1)
B. y 2 3(x 1)
④若
x0 3
y0
1 ,则直线 (x0
1)( y 2)
( y0
暑期高一升高二复习检测卷

暑期补习检测时间:90分钟 满分:110分一.不定项选择题(本题共10个小题,每小题6分,共60分,在每个小题给出的四个选项中,有些只有一个符合题意,有些有多个符合题意,全对得6分,对而不全得3分)1. 关于曲线运动,下列说法中正确的是 ( )A .曲线运动一定是变速运动B .曲线运动速度的方向不断变化,但速度的大小可以不变C .曲线运动的速度方向可能不变D .曲线运动的速度大小和方向一定同时改变2. 如右图所示,A 和B 的质量分别是1kg 和2kg ,弹簧和悬线的质量不计,在A 上面的悬线烧断的瞬间,A 和B 的加速度分别等于( )A.3g ,0B. 0 , 3gC.g ,0D.0, g3. 一艘船在静水中的速度为3m/s ,今欲过一条宽为60 m 的河,若已知水的流速为4 m/s,则船过河的最短时间为( )A.20sB. 15sC.12sD.60s4. 如图所示,虚线a 、b 、c 代表电场中三个等势面,相邻等势面之间的电势差相等,即U ab =U bc ,实线为一带正电的质点仅在电场力作用下通过该区域时的运动轨迹,P 、Q 是这条轨迹上的两点,据此可知( )A .三个等势面中,a 的电势最小B .带电质点在P 点具有的电势能比Q 点具有的电势能大C .带电质点通过P 点时的动能比通过Q 点时大D .带电质点通过P 点时的加速度比通过Q 点时小5. .如图所示在粗糙水平面上固定一点电荷Q,在M 点无初速释放一带有恒定电量的小物块,小物块在Q 的电场中运动到N 点静止,则从M 点运动到N 点的过程中( )A 、小物块所受电场力逐渐减小B 、小物块具有的电势能逐渐减小C 、M 点的电势一定高于N 点的电势D 、小物块电势能的变化量的大小一定等于克服摩擦力做的功6.如图所示,一个正检验电荷q 在正点电荷Q 的电场中,沿某一条电场线向右运动,已知它经过M 点的加速度是经过N 点时加速度的2倍,则( )A 、它经过M 点时的速度是经过N 点的2倍B 、它经过N 点时的速度是经过M 点时的速度的2倍C 、MQ 之间的距离是NQ 之间的距离的1/2D 、NQ 之间的距离是MQ 之间距离的2倍7. 三段不可伸长的细绳OA 、OB 、OC 共同悬挂一重物,如图所示,B 端固定,OB 始终保持水平,A 端水平向左移动一小段距离的过程中,下面说法正确的是( )A、OA 绳拉力减少 B、OA 绳拉力增大C、OB 绳拉力减少 D、OC 绳拉力增大8. 如图所示,一个小物体A 放在斜面B 上,B 放于光滑的水平地面上,现用水平恒力F 推B 使A 和B 相对静止一起通过一段路程,在这个过程中,以下哪些力有可能作正功( )A .A 受的重力B .B 受的摩擦力C .A 受的支持力D .B 受的压力9. 如图2所示,传送带以0υ的初速度匀速运动。
9.暑假高一升高二学案 综合练习
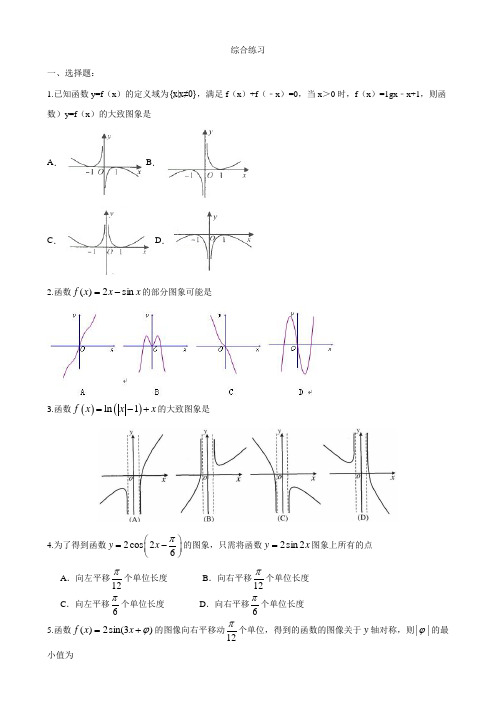
综合练习一、选择题:1.已知函数y=f (x )的定义域为{x|x≠0},满足f (x )+f (﹣x )=0,当x >0时,f (x )=1gx ﹣x+1,则函数)y=f (x )的大致图象是A .B .C .D .2.函数x x x f sin 2)(-=的部分图象可能是3.函数()()ln 1f x x x =-+的大致图象是4.为了得到函数2cos 26y x π⎛⎫=- ⎪⎝⎭的图象,只需将函数x y 2sin 2=图象上所有的点 A .向左平移12π个单位长度 B .向右平移12π个单位长度 C .向左平移6π个单位长度 D .向右平移6π个单位长度5.函数)3sin(2)(ϕ+=x x f 的图像向右平移动12π个单位,得到的函数的图像关于y 轴对称,则||ϕ的最小值为A .12π B .4πC .43πD .125π6.已知函数1()),(0,),(,0)23f x x A πωϕωϕ=+><为()f x 图像的对称中心,若该图像上相邻两条对称轴间的距离为2,则()f x 的单调递增区间是A.24(2,2),33k k k Z -+∈ B.24(2,2),33k k k Z ππππ-+∈ C. 24(4,4),33k k k Z -+∈ D.24(4,4),33k k k Z ππππ-+∈7.2cos 0444x x x m +-≥对于,33ππ⎡⎤∀∈-⎢⎥⎣⎦x 恒成立,则实数m 的取值范围是A .(,-∞B .⎛-∞ ⎝⎦C .⎣D .)+∞ 8.以角θ的顶点为坐标原点,始边为x 轴的非负半轴,建立平面直角坐标系,角θ的终边过点P (1,2),则tan()4πθ+=______.9.已知4sin 85πα⎛⎫-= ⎪⎝⎭,则3cos 8πα⎛⎫+= ⎪⎝⎭A .45-B .45 C.35- D .3510.已知α,β为锐角,且1tan 7α=,()cos αβ+=,则cos 2β=A .35 B .23 C .45D11.设π(0,)2α∈,π(0,)2β∈,且cos 1cos sin sin αβαβ-=,则 A .π2αβ+=B .π22βα+=C .π22βα-=D .π22βα-=12.已知三棱锥S -ABC ,△ABC 是直角三角形,其斜边AB =8,SC ⊥平面ABC ,SC =6,则三棱锥的外接球的表面积为(A )64π (B )68π (C )72π (D )100π13.三棱锥A BCD -中,AD ⊥平面BCD ,1AD =,BCD ∆是边长为2的等边三角形,则该几何体外接球的表面积为 A .176π B .196π C .173π D .193π 14.,,,A B C D 是同一球面上的四个点,ABC ∆中,23BAC π∠=,AB AC =,AD ⊥平面ABC ,6AD =,AB =,则该球的表面积为 .15.已知△ABC 中,角A 、B 、C 所对边分别为a 、b 、c ABC 面积的最大值为__________.16.下列函数中既是偶函数,又在(0,1)上单调递增的是 (A )cos y x = (B)y =(C )2x y = (D )lg y x =17..若函数()()log 20,1x a f x x a a -=->≠的两个零点是,m n ,则A .1mn =B .1mn > C. 1mn < D .以上都不对18.已知函数213,1()log ,1x x x f x x x ⎧-+≤⎪=⎨>⎪⎩,若对任意的x R ∈,不等式25()4f x m m ≤-恒成立,则实数m 的取值范围为A .1[1,]4- B .1[,1]4 C.1[2,]4- D .1[,1]319.若函数()()22,20,11,02,x x x f x f x x ⎧+-≤≤⎪=⎨-+<≤⎪⎩,则关于x 的方程()0x f x -=在[]2,2-上的根的个数为A .6B .5C .4D .320.定义在R 上的函数()f x 满足()()4f x f x +=,()21,1121,13x x f x x x ⎧-+-≤≤⎪=⎨--+<≤⎪⎩.若关于x 的方程()0f x ax -=有5个不同实根,则正实数a 的取值范围是(A )11,43⎛⎫⎪⎝⎭ (B )11,64⎛⎫ ⎪⎝⎭(C)1166⎛⎫- ⎪⎝⎭ (D)1,86⎛- ⎝21.已知函数()sin()4f x x πω=+(02)ω<≤,直线4x π=为()y f x =图象的一条对称轴.(1)求函数()f x 的解析式;(2)在ABC ∆中,角A ,B ,C 的对边的边分别为a ,b ,c ,若()1f A =且,2a =,求ABC ∆的面积最大值.22.在锐角ABC ∆中,A B C 、、角所对的边分别为a b c 、、,且cos cos 23sin a B b A C c +=.(1)求C ∠; (2)若2sin aA=,求ABC ∆面积S 的最大值.23.如图,在ABC ∆中,2AB =,1cos 3B =,点D 在线段BC 上. (1)若2BD DC =,ACD ∆的面积为423,求边AC 的长; (2)若23ADC π∠=,求三角形ABD 的面积ABD S ∆.()=m f x n ⋅ 24.ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,已知cos sin b C b C a +=. (Ⅰ)求角B 的大小; (Ⅱ)若BC 边上的高等于14a ,求cos A 的值.25.已知向量m =(cosx-1,3sinx),n =(cosx+1,cosx),x R ∈. (1)求()x f 的单调递增区间;(2)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,若ccosB+bcosC=1且()f A =0,求ABC ∆面积最大值.26.已知△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且asinA=bsinB+(c ﹣b )sinC . (1)求角A 的大小; (2)若b=2,S △ABC =,求sin (2B ﹣A )的值.27.在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c 3sin a bB=. (Ⅰ)求角A 的值; (Ⅱ)若6B π=,且ABC ∆的面积为3BC 边上的中线AM 的大小.。
高一升高二数学暑期衔接自主学习练习题

A 为锐角
A 为钝角或直角
图形
关系式
解的 个数
(3)已知三边,用____________定理.有解时,只有一解. (4)已知两边及夹角,用____________定理,必有一解. 4.三角形中的常用公式及变式
(1)三角形面积公式 S△=
=
=
=
=
.其中 R,r 分别为三角形外接圆、内切圆
半径.
(2)A+B+C=π,则 A=____________,A=_____________,从而 sinA= 2
,φ角所在象限与点(a,b)所在象限_______.
§6 正弦定理、余弦定理及其应用
1.正弦定理
(1)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,
即
.其中 R 是三角形外接圆的半径.
(2)正弦定理的其他形式:
①a=2RsinA,b=____________,c=____________;
=x=________,MP=y=________,AT=
=________.像 OM,MP,AT
这种被看作带有方向的线段,叫做有向线段,这三条与单位圆有关的有向线段
MP,OM,AT,分别叫做角α的_______、_______、_______,统称为三角函数线.
5.特殊角的三角函数值
角α 0° 30° 45° 60° 90° 120° 135° 150° 180° 270° 360°
①终边在 x 轴非负半轴上的角的集合可记
作
;
②终边在 x 轴非正半轴上的角的集合可记
作
;
③终边在 y 轴非负半轴上的角的集合可记
作
;
④终边在 y 轴非正半轴上的角的集合可记
暑期高一升高二数学试卷

?
21.已知函数 其中 在 中, 分别是角的对边,且 .
(1)求角A;
(2)若 , ,求 的面积.
(
22.设数列 的前 项和为 ,若对于任意的正整数 都有 ,
(1)、设 ,求证:数列 是等比数列,并求出 的通项公式;
(2)、求数列 的前 项和 。
参考答案
一、选择题
1-5 DBBBB 6-10 CDDAB 11-12 BD
}
18.如图,四棱锥 中, 是正三角形,四边形 是矩形,且平面 平面 , , .
(1)若点 是 的中点,求证: 平面
(2)若 是线段 的中点,求三棱锥 的体积.
.
19.如图,在四棱锥 中, 底面 , , , 是 的中点
(1)证明 ;
(2)证明 平面 ;
!
20.已知函数
(1)求函数 的单调递增区间;
(2)若 , 的值.
二、填空题
13.314. 15.(1) (2)
解:(1)因为 ,
;
(2)
因为 的解集为 ,
所以 的解集为 ,
所以4和3为 的两根,
故 ,
解得: .12分
18.解:(1)证明:设 ,连接 ,
由三角形的中位线定理可得: ,3分
∵ 平面 , 平面 ,∴ 平面 .6分
(2)∵平面 平面 ,
2015年8月考试试卷
1、选择题(每题6分,共60分)
1.已知全集U=R,A={y|y=2x+1},B={x|lnx<0},则(∁UA)∩B=( )
A.∅ B.{x| <x≤1} C.{x|x<1} D.{x|0<x<1}
2.指数函数 在R上是增函数,则 的取值范围是( )
A. B. C. D.
2022年暑假高一升高二数学练习

2022年暑假高一升高二数学练习一、单选题1.已知O 为正三角形ABC 的中心,则向量OA 在向量AB 上的投影向量为( )A .AB B ABC .12AB -D .12AB 2.设0b a >>,则下列不等关系正确的是( ) A .11a b< B .01a b<< C .2a b b +>D .b a a b< 3.记n S 为等差数列{}n a 的前n 项和,且122a =,716S S =,则n S 取最大值时n 的值为( ) A .12B .12或11C .11或10D .104.已知数列{}n a 满足130n n a a ++=,243a =-,则{}n a 的前10项和等于( )A .()10613---B .()101139- C .()10313--D .()10313+5.已知四个选项中的图形棱长都相等,且P ,Q ,R ,S 分别是所在棱的中点,则这四个点不共面的是( )A .B .C .D .6.在ABC 中,()7sin sin 2213A A ππ⎛⎫+++= ⎪⎝⎭,则tan A 的值是( )A .125- B .125 C .512- D .5127.设甲、乙两楼相距10m ,从乙楼底望甲楼顶的仰角为60︒,从甲楼顶望乙楼顶的仰角为30,则甲、乙两楼的高分别是( )A B .C .D . 8.如图所示,在ABC 中,点M 是AB 的中点,且1,2AN NC BN =与CM 相交于点E ,若AE AB AC λμ=+,则,λμ满足( ) A .45λμ+= B .2λμ= C .25λμ-=D .12λμ= 9.十二平均律是我国明代音乐理论家和数学家朱载堉发明的,明万历十二年(公元1584年),他写成《律学新说》提出了十二平均律的理论十二平均律的数学意义是:在1和2之间插入11个数使包含1和2的这13个数依次成递增的等比数列,记插入的11个数之和为M ,插入11个数后这13个数之和为N ,则依此规则,下列说法错误的是( ) A .插入的第8个数为34 B .插入的第5个数是插入的第1个数的32倍 C .3M >D .7N <10.已知直线l ,m ,平面,αβ,下列叙述正确的是( ) A .,l l βααβ⊂⇒∥∥B .,,,l m l m ββαααβ⊂⊂⇒∥∥∥C .,,l m l m αβαβ⊂⊂⇒∥∥D .,,,,l m l m lm M ββαααβ⊂⊂=⇒∥∥∥11.如图所示,已知四棱锥P ABCD -,底面ABCD 为菱形,且PA ⊥底面ABCD ,M 是PC 上的任意一点,则下列选项能使得平面MBD ⊥平面PCD的是( )A .M 为PC 的中点B .DM BC ⊥C .DM PC ⊥D .DM PB ⊥12.在ABC 中,内角,,A B C 所对的边分别为,,a b c ,且125sin cos sin cos ,cos ,235a A C c A A c Bb +===,则ABC 的面积为( )A .32B .2C .3D .5二、填空题13.函数()2sin f x x ω=,0>ω的部分图象如图所示,则()()()()1232024f f f f ++++=______.14.如图,点P 在正方体1111ABCD A B C D -的面对角线1BC 上运动,则下面四个结论:①,点P 到平面1ACD 的距离不变;①1A P //平面1ACD ;①1DP BC ;①平面1PDB 平面1ACD .其中正确结论的序号是_____________.(写出所有你认为正确结论的序号)15.记等比数列{}n a 的前n 项和为Sn ,若2462S S S +=,则{}n a 的公比为______ 16.如图,在矩形ABCD 中,M ,N 分别为线段BC ,CD 的中点,若12MN AM BN λλ=+,12,R λλ∈,则12λλ+的值为___________. 三、解答题17.如图,在三棱锥P ABC -中,PA ⊥底面ABC ,90BAC ∠=.点,,D E N 分别为棱,,PA PC BC 的中点,M 是线段AD 的中点,4PA AC ==,2AB =.(1)证明:平面PAB ⊥平面BDE ;(2)已知点F 在AB 上,且平面//MNF 平面BDE ,求线段AF 的长.18.已知等比数列{}n a 的公比大于1,26a =,1320a a +=. (1)求{}n a 的通项公式; (2)若12331log log 22n n n n b a a a ++=+,求{}n b 的前n 项和n T .19.设函数()()2cos 2104f x a x a π⎛⎫=++≠ ⎪⎝⎭.(1)当1a =时,求()f x 的减区间;(2)若0,2x π⎡⎤∈⎢⎥⎣⎦时,()f x 的最大值为3,求实数a 的值.20.设数列{}{}n n a b 、 的前n 项和分别为n n S T 、 ,且21(37)2n S n n =+,2(1)(N*)n n T b n =-∈ . (1)求数列{}{}n n a b 、的通项公式; (2)令n n n c a b = ,求{}n c 的前n 项和n U .21.如图,A ,B 是某海域位于南北方向相距15(13)+海里的两个观测点,现位于A 点北偏东45︒,B 点南偏东30的C 处有一艘渔船遇险后抛锚发出求救信号,位于B 点正西方向且与B 点相距50海里的D 处的救援船立即前往营救,其航行速度为40海里/时. (1)求B ,C 两点间的距离;(2)该救援船前往营救渔船时应该沿怎样的方向航行?救援船到达C 处需要多长时间?(角度精确到0.01︒)(参考数据:sin21.790.37,cos21.790.93≈≈︒︒)22.在如图所示的半圆柱中,AB 为上底面直径,DC 为下底面直径,AD 为母线,点F 在AB 上,点G 在DC 上且222AB AD BF DG ====,P 为DC 的中点.(1)求直线AG 与直线BF 所成角的余弦值; (2)求直线CA 与平面ADG 所成角的正切值; (3)求二面角A GC D --的正弦值.2022年暑假高一升高二数学练习参考答案1.C取AB 中点D ,连接OD ,因为O 为正三角形ABC 的中心,故⊥OD AB ,则向量OA 在向量AB 上的投影向量为12DA AB =-故选:C 2.B令2a =,3b =,满足0b a >>, 但111123a b =>=,526a b b +=<=,3223b a a b =>=,故A ,C ,D 错误. 由0b a >>,得10b >,所以10ab>>,故B 正确.故选:B. 3.B解:设等差数列{}n a 的公差为d ,由716S S =,得1172116120a d a d +=+,即1110a d +=, 又122a =,所以2d =-,所以()2221242n a n n =--=-,令0n a =,可得12n =, 所以数列{}n a 满足:当11n ≤时,0n a >;当12n =时,0n a =;当13n ≥时,0n a <, 所以n S 取得最大值时,n 的取值为11或12. 4.C由题113n n a a +=-,243a =-,所以1234a a =-⨯=,所以{}n a 是公比13q =- 的等比数列,14a = ,()101010101111343131113q S a q -⎛⎫-- ⎪-⎝⎭=⋅=⨯=--⎛⎫-- ⎪⎝⎭;故选:C.5.D在A 图中,分别连接,,,PS QR AB CD ,由正方体可得四边形ABCD 为矩形,则//AB CD ,因为,P S 为中点,故//PS AB ,则//PS QR ,所以,,,P S R Q 四点共面. 在B 图中,设,E F 为所在棱的中点,分别连接,,,,,PS SR RF FQ EQ PE , 由A 的讨论可得//PS ER ,故,,,P S E R 四点共面,同理可得//ER QF ,故//PS QF ,同理可得//EP RF ,//SR EQ故F ∈平面PRS ,Q ∈平面PRS ,所以,,,,,P S R Q E F 六点共面. 在C 图中,由,P Q 为中点可得//PQ AB ,同理//RS AB , 故//PQ RS ,所以,,,P S R Q 四点共面. 在D 图中,,PQ RS 为异面直线, 故选:D. 6.A解:在ABC 中,()7sin sin 2sin cos 213A A A A ππ⎛⎫+++=+= ⎪⎝⎭,平方得4912sin cos 169A A +=,1202sin cos 169A A =-,因为A 为三角形的一个内角,所以sin 0A >,cos 0A <, 所以sin cos 0A A ->,()2289sin cos 12sin cos 169A A A A -=-=, 所以17sin cos 13A A -=,结合7sin cos 13A A +=,可得12sin 13A =,5cos 13A =-, 所以sin 12tan cos 5A A A ==-.故选:A. 7.D设甲、乙两楼分别为,AB CD ,如图,由题意可知10,60,30BC ACB DAE ︒=∠=∠=︒. 在Rt ABC △中,tan 3ABACB BC∠==,①103AB =. 由10AE BC ==,在Rt ADE △中,3tan 3DE DAE AE ∠==,得1033DE =, ①4033CD CE DE AB DE =+=+=. 故选:D . 8.B 由1,2AN NC =得31,AN AC = 因为点M 是AB 的中点,所以1,2AM AB =由,,N E B 三点共线知,存在实数m ,满足()()1311AE mAN m AB mAC m AB =+-=+-,由,,C E M 三点共线知,存在实数n ,满足()()1112AE nAM n AC nAB n AC =+-=+-,所以()()111123mAC m AB nAB n AC +-=+-,又因为,AC AB 为不共线的非零向量,所以112113m n m n-==-⎧⎪⎪⎨⎪⎪⎩,解得3545m n ⎧⎪⎪⎨==⎪⎪⎩,所以2155AE AB AC =+,即21,55λμ==, 所以213555λμ+=+=,故A 不正确;25215λμ==,故B 正确;D 不正确;211555λμ-=-=,故C 不正确.故选:B.9.D设该等比数列为{}n a ,公比为q ,则1131,2a a ==,故121312a q a ==. 对于A :插入的第8个数为891a a q =⨯故A 正确;对于B :插入的第5个数为561a a q =⨯,插入的第1个数为21a a q =⨯,所以546121a a q q a a q⨯===⨯正确; 对于C:1121121(1)11112a q M q--===----.要证3M >,即证11211312-->-,即证1121421>-,即证112524>,即证12524⎛⎫> ⎪⎝⎭, 而26132542⎛⎫⎫>> ⎝ ⎪⎪⎭⎛⎝⎭成立,故C 正确; 对于D :3N M =+.因为()()12636 1.4 1.925⎛⎫>>> ⎪⎝⎭,所以112625>,所以1121521>-,所以11211412-->-,即4M >,所以37N M =+>故D 错误.故选:D 10.D解:如图,在长方体1111ABCD A B C D -中,直线//AB 平面1DC ,直线AB 平面AC ,但是平面AC 与平面1DC 不平行,所以选项A 错误.取1BB 的中点E ,1CC 的中点F ,连接EF ,则//EF 平面11,//AC B C 平面AC .又EF ⊂平面111,BC B C ⊂平面1BC ,但是平面AC 与平面1BC 不平行,所以选项B 错误.直线11,AD B C AD ⊂∥平面AC ,11B C ⊂平面1BC ,但平面AC 与平面1BC 不平行,所以选项C 错误.选项D 是两个平面平行的判定定理,所以选项D 正确.故选:D 11.C如图,连接AC ,①底面ABCD 为菱形,①BD AC ⊥, ①PA ⊥底面,ABCD BD ⊂底面ABCD ,①PA BD ⊥, ①PAAC A =,PA ⊂平面PAC ,AC ⊂平面PAC ,①BD ⊥平面PAC ,①PC ⊂平面PAC ,①BD PC ⊥, 当PC 上的点M 满足DM PC ⊥时,BD ⊂平面MBD ,DM ⊂平面MBD ,BD DM D ⋂=①PC ⊥平面MBD ,又PC ⊂平面PCD ,①平面MBD ⊥平面PCD , 则当DM PC ⊥时,平面MBD ⊥平面PCD . 故选:C . 12.A解:由正弦定理得21sin cos sin sin cos sin 3A C C A A C +=,①ABC π++=,①2sin cos sin sin cos sin (sin cos cos sin )A C C A A A A C A C +=+ 1sin sin()sin sin sin 3A A C ABC =+==,①25(0,),cos 5B B π∈=,①5sin 5B =, ①51sin sin 53A C =,由正弦定理得5153a c =,①53a c =, 由余弦定理得22222225422cos 2939b ac ac B c c c c =+-=+-==,解得3c =,①5a =,①1153sin 532252ABC S ac B ==⨯⨯⨯=△.故选:A . 13.0由图象可知,函数()f x 的周期T =8, 所以284ππω==,故()2sin 4f x x π=,因为()()()()12380f f f f ++++=,20248253=⨯, 所以()()()()12320240f f f f ++++=.14.-1因为{}n a 是等比数列,设{}n a 的公比为q , 若1q ≠时,由2462S S S +=可得()()()6241111112111a q a q a q q q q---=+---, 整理得6242q q q =+,因为0q ≠,所以4221q q =+即()22221q q =+, 解得212q =-(舍去)或21q =,因为1q ≠,所以1q =-,若1q =时,616S a =,241111243622S S a a a a ++==≠,所以舍去, 综上所述,1q =-, 15.①①①连接11111,,,,AC A C A B AD D C . 因为11//AA CC ,11AA CC =, 所以四边形11AAC C 是平行四边形, 所以11//AC A C .又AC ⊄平面1111,A BC A C 平面11A BC ,所以//AC 平面11A BC . 同理可证1//AD 平面11A BC , 又AC ⊂平面11,ACD AD 平面1ACD ,且1ACAD A =,所以平面1//ACD 平面11A BC . 因为1A P ⊂平面11A BC ,所以1//A P 平面1ACD ,故①正确. 因为1BC ⊂平面11A BC , 所以1//BC 平面1ACD ,所以点P 到平面1ACD 的距离不变,故①正确. 连接1,,DB DC DP .因为1DBDC ,所以当P 为1BC 的中点时才有1DP BC ,故①错误.因为1BB ⊥平面,ABCD AC 平面ABCD ,所以1AC BB ⊥. 又1,ACBD BB BDB ,1,BB BD ⊂平面11BB D D ,所以AC ⊥平面11BB D D .连接1B D ,又1B D ⊂平面11BB D D , 所以1B DAC .同理可证11B DAD .又AC ⊂平面11,ACD AD 平面1ACD ,1AC AD A =,所以1B D ⊥平面1ACD .又1B D ⊂平面1PDB , 所以平面1PDB 平面1ACD ,故①正确.故答案为:①①①. 16.25因为M ,N 分别为线段BC ,CD 的中点, 所以()11112222MN BD AD AB AD AB -===-, 12AM AB BM AB AD =+=+, 12AD A B BC CN B N =+=-, 所以12121122MN AM BN AB AD AD AB λλλλ⎛⎫⎛⎫=+=++- ⎪ ⎪⎝⎭⎝⎭12121122A AB D λλλλ⎛⎫=++ ⎛⎫- ⎪⎝⎪⎝⎭⎭,所以121211221122λλλλ⎧⎪⎪⎨⎪+=-=⎩-⎪,解得121535λλ⎧⎪=-⎨=⎪⎪⎪⎩,所以12132555λλ+=-+=,所以12λλ+的值为25.17.(1),D E 分别为,PA PC 中点,//DE AC ∴,又90BAC ∠=,DE AB ⊥∴; PA ⊥平面ABC ,AC ⊂平面ABC ,PA AC ∴⊥,又//DE AC ,DE PA ∴⊥; PA AB A =,,PA AB ⊂平面PAB ,DE ∴⊥平面PAB ,又DE ⊂平面BDE ,∴平面PAB ⊥平面BDE .(2)平面//MNF 平面BDE ,MF ⊂平面MNF ,//MF ∴平面BDE , MF ⊂平面PAB ,平面PAB ⋂平面=BDE BD ,//∴MF BD ,又M 为AD 中点,F ∴为AB 中点,112AF AB ∴==. 18.(1)设等比数列{}n a 的公比为()1q q >,由26a =,1320a a +=得6620q q+=, 解之得3q =或13q =(舍去), 由26a =得,12a =,所以{}n a 的通项公式为123n n a -=⋅.(2)由(1)知,()1112331111232311log log 22n n n n n n b a a a n n n n --++=+=⋅+=⋅+-++所以{}n b 的前n 项和为()01111111233312231n n T n n -⎡⎤⎛⎫⎛⎫⎛⎫=++⋅⋅⋅++-+-+⋅⋅⋅+- ⎪ ⎪ ⎪⎢⎥+⎝⎭⎝⎭⎝⎭⎣⎦ 131********n n n n -=⨯+-=--++ 19.(1)解:当1a =时,()2cos 214f x x π⎛⎫=++ ⎪⎝⎭, 令()2224k x k k ππππ≤+≤+∈Z ,得()388k x k k ππππ-+≤≤+∈Z , 故()f x 的减区间为()3,88k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z . (2)解:当0,2x π⎡⎤∈⎢⎥⎣⎦时,52,444x πππ⎡⎤+∈⎢⎥⎣⎦,所以cos 21,42x π⎡⎛⎫+∈-⎢ ⎪⎝⎭⎣⎦, 当0a >时,cos 24x π⎛⎫+= ⎪⎝⎭()max 213f x a ==,解得a = 当0a <时,cos 214x π⎛⎫+=- ⎪⎝⎭时,()max 213f x a =-+=,解得1a =-. 综上,1a =-或a =20.(1)由21(37)2n S n n =+得115a S ==,当2n ≥时,()()22111(37)317122n n n a S S n n n n -⎡⎤=-=+--+-⎣⎦32n =+, 当1n =时,1325a =+=也适合,故32n a n =+.由2(1)n n T b =-得1112(1)b T b ==-,得12b =,当2n ≥时,112(1)2(1)n n n n n b T T b b --=-=---,得12n n b b -=,又12b =,所以12n n b b -=,所以数列{}n b 是首项为2,公比为2的等比数列, 所以1222n n n b -=⨯=,综上所述:32n a n =+,2n n b =.(2)(32)2n n n n c a b n ==+⨯,所以1235282112(32)2n n U n =⨯+⨯+⨯+++⨯,所以234125282112(32)2n n U n +=⨯+⨯+⨯+++⨯,所以2312523(222)(32)2n n n n U U n +-=⨯++++-+⨯, 所以23143(2222)(32)2n n n U n +-=+++++-+⨯12(12)43(32)212n n n +-=+⨯-+⨯- (62)22n n =-+⨯-,所以1(31)22n n U n +=-⨯+.21.(1)在ABC 中,45,30BAC ABC ∠∠=︒=︒,则105ACB ∠=︒,()sin105sin 6045sin 60cos 45cos 60sin 45=+=︒︒︒︒︒︒︒+=12=, 由正弦定理sin sin BC AB BAC ACB =∠∠,得sin sin AB BAC BC ACB ∠==∠15(130==(海里), 故B ,C 两点间的距离为30海里.(2)在BCD △中,120DBC ∠=︒,由余弦定理得2222cos DC DB BC DB BC DBC =+-⋅∠=22503025030cos1204900︒+-⨯⨯⨯=,则70DC =(海里),所以救援船到达C 处需要的时间70 1.7540t ==(时). 由余弦定理可得222222507030cos 0.93225070DB DC BC D DB DC +-+-==≈⋅⨯⨯.又D 为锐角,所以21.79D =︒,所以9021.7968.21︒-︒=︒.故救援船前往营救渔船时应该沿南偏东68.21︒方向航行,到达C 处需要1.75小时. 22.(1)过F 点作圆柱的母线FH 交DC 于H ,因为FH 与BC 均为圆柱的母线,所以FH BC ∥且FH BC =,所以四边形BCHF 为平行四边形,所以FB HC ∥且1FB HC ==,所以PCH △为正三角形.又因为DPG △为正三角形,所以60HCP GPD ∠=∠=︒,CH GP ∥,所以BF CH GP ∥∥,所以AGP ∠或其补角为直线AG 与BF 所成的角.在APG 中,5AG =,1GP =,5AP =,所以由余弦定理知:22215cos 21025AG GP AP AGP AG GP +-∠===⨯,所以直线AG 与直线BF 所成角的余弦值为510.(2)因为AD ⊥平面DCG ,CG ⊂平面DCG ,所以CG AD ⊥又因为CG DG ⊥,AD DG D =,,AG AD ⊂平面ADG ,所以CG ⊥平面ADG ,所以CAG ∠为直线CA 与平面ADG 所成的角,在Rt CAG △中5AG =,22213GC =-=,15tan 5GC CAG AG ∠==.(3)由(2)知CG ⊥平面ADG ,AG ⊂平面ADG ,所以CG AG ⊥,CG DG ⊥,因此AGD ∠为二面角A GC D --的平面角,在Rt ADG 中,2AD =,5AG =,25sin 5AD AGD AG ∠==.所以二面角A GC D --的正弦值为255.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年8月考试试卷一、选择题(每题6分,共60分)1.已知全集U=R ,A={y|y=2x +1},B={x|lnx <0},则(∁U A )∩B=( ) A.∅ B.{x|<x≤1} C.{x|x <1} D.{x|0<x <1}2.指数函数()(1)xf x a =-在R 上是增函数,则a 的取值范围是( ) A .1a > B .2a > C .01a << D .12a << 3.已知0.6log 0.5a =,ln0.5b =,0.50.6c =.则( )(A )>>a b c (B )>>a c b (C )>>c a b (D )>>c b a 4.已知点(1,1)A ,(4,2)B 和向量=(2,)a λ,若//a AB ,则实数λ的值为( ) A .23-B .23C .32D .32- 5.在等差数列{}n a 中,5,142==a a ,则{}n a 的前5项和=5S ( ) A .7 B.15 C.20 D.256.过点()1,0且与直线220x y --=垂直的直线方程是( )A.210x y --=B.210x y -+=C.220x y +-=D.210x y +-= 7.直线被圆所截得的弦长为( )A. B.1 C. D.8.若,则的最小值为( )A. 1B. 2C. 3D. 49.若实数,x y 满足2210x y +-=,则12y z x -=+的取值范围是( )A.4,03⎡⎤-⎢⎥⎣⎦B.40,3⎡⎤⎢⎥⎣⎦C.22,3⎡⎤--⎢⎥⎣⎦D.10,23⎡⎤--⎢⎥⎣⎦ 10.若直线m l ,与平面α、β、γ满足,l l βγ=∥α,,m m αγ⊂⊥,则有( )A .m ∥β且l m ⊥B .α⊥γ且l m ⊥C .α⊥β且m ∥γD .α∥β且α⊥γ11.在正三棱锥P ABC 中,D ,E 分别是AB ,BC 的中点,下列结论:①AC ⊥PB ;②AC ∥平面PDE ;③AB ⊥平面PDE ,其中错误的结论个数是( ) A .0 B .1 C .2 D .312.函数()si ()n f x A x ωϕ=+(000A ωϕπ>><<,,)的图象如图所示,则()4f π的值为( )A .2B .0C .1D .3二、填空题(每空5分,共20分)13.圆的圆心到直线的距离 . 14.已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是 错误!未找到引用源。
.15.如图,已知正方体1111ABCD A B C D -中,,E F 分别是1,AD AA 的中点.则直线1AB 和EF 所成的角为__________.16.函数π()3sin 23f x x ⎛⎫=-⎪⎝⎭的图象为C ,如下结论中正确的是__________ ①图象C 关于直线11π12x =对称;②图象C 关于点2π03⎛⎫⎪⎝⎭,对称; ③函数()f x 在区间π5π1212⎛⎫-⎪⎝⎭,内是增函数;④由3sin 2y x =的图象向右平移π3个单22:2440C x y x y +--+=:3440l x y ++=d =位长度可以得到图象C 三、解答题17.设集合A={x|x 2<9},B={x|(x-2)(x+4)<0}. (1)求集合A∩B;(2)若不等式2x 2+ax+b <0的解集为A ∪B ,求a ,b 的值.18.如图,四棱锥BCDE A -中,ABC ∆是正三角形,四边形BCDE 是矩形,且平面⊥ABC 平面BCDE ,2=AB ,4=AD .(1)若点G 是AE 的中点,求证://AC 平面BDG(2)若F 是线段AB 的中点,求三棱锥EFC B -的体积.19.如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,60AB AD AC CD ABC ⊥⊥∠=,,°,PA AB BC ==,E 是PC 的中点 (1)证明CD AE ⊥;(2)证明PD ⊥平面ABE ;AB CDE20.已知函数.1cos sin 3cos )(2+-=x x x x f (1)求函数)(x f 的单调递增区间; 5ππ221.已知函数(),f x m n =⋅其中(1,sin 2),m x =(cos 2n x =在ABC ∆中,,,a b c 分别是角的对边,且()1f A =. (1)求角A;(2)若a =3b c +=,求ABC ∆的面积.22.设数列{}n a 的前n 项和为n S ,若对于任意的正整数n 都有n a S n n 32-=, (1)、设3+=n n a b ,求证:数列{}n b 是等比数列,并求出{}n a 的通项公式; (2)、求数列{}n na 的前n 项和n T 。
参考答案一、选择题1-5 DBBBB 6-10 CDDAB 11-12 BD 二、填空题 13.3 14.4315. 60 16.①②③ 三、解答题17.(1){x |3x 2}-<<(2)2,24a b ==- 解:(1)因为2A {x |x 9}{x |3x 3}==-<<<,B {x |x 24)0}{x |4x 2}=-+=-()(x <<<.A B {x |3x 3}{x |4x 2}{x |3x 2}∴=--=-<<<<<<;(2)AB {x |3x 3}{x |4x 2}{x |4x 3}=--=-<<<<<<因为220x ax b ++<的解集为AB ,所以220x ax b ++<的解集为{x |4x 3}-<<, 所以 4和3为220x ax b ++<的两根,故⎪⎪⎩⎪⎪⎨⎧⨯-=+-=-342342b a,解得:2,24a b ==-. 12分 18.解:(1)证明:设CE BD O ⋂=,连接OG ,6分 8分又∵F 是AB 的中点,ABC ∆是正三角形, -12分19.(Ⅰ)证明:在四棱锥P ABCD -中,因PA ⊥底面ABCD ,CD ⊂平面ABCD ,故PA CD ⊥ AC CD PA AC A ⊥=,∵,CD ⊥∴平面PAC而AE ⊂平面PAC ,CD AE ⊥∴(2)证明:由PA AB BC ==,60ABC ∠=°,可得AC PA =E ∵是PC 的中点,AE PC ⊥∴由(1)知,AE CD ⊥,且PCCD C =,所以AE ⊥平面PCD而PD ⊂平面PCD ,AE PD ⊥∴PA ⊥∵底面ABCD PD ,在底面ABCD 内的射影是AD ,AB AD ⊥,AB PD ⊥∴又ABAE A =∵,综上得PD ⊥平面ABE(3)解法一:过点A 作AM PD ⊥,垂足为M ,连结EM 则(2)知,AE ⊥平面PCD ,AM 在平面PCD 内的射影是EM ,则EM PD ⊥因此AME ∠是二面角A PD C --的平面角 由已知,得30CAD ∠=° 设AC a =,可得32PA a AD PD a AE a ====,,,ABD在ADP Rt △中,AM PD ⊥∵,AMPD PA AD =∴··,则73a PA ADAM a PD===··在AEM Rt △中,sin 4AE AME AM ==20.(1) 5,,36k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦;(2)sin 2θ=解:1cos 2133(1)()21cos 22cos(2)2222232x f x x x x x π+=-+=-+=++ 52222, ,3365(),,.36k x k k x k f x k k k Z πππππππππππππ+≤+≤++≤≤+⎡⎤++∈⎢⎥⎣⎦令得故的单调增区间为5352(2)(),cos(2), cos(2)632633f ππθθθ=∴+∴++==-,25()23333ππππθπθ∈⇒<+<,, sin(2)33πθ∴+ sin 2sin (2)sin(2)cos cos(2)sin 3333336ππππππθθθθ⎡⎤∴=+-=+-=⎢⎥⎣⎦+12分21.解:(1)因为)62sin(22sin 32cos )(π+=+=⋅=x x x n m x f ,且()1f A =.所以1)62sin(2=+πA ,可得266A ππ+=或56π. 解得3A π=或0A =(舍)(2)由余弦定理得cos A =223bc b c =+-联立方程 3b c += 解得 21b c =⎧⎨=⎩ 或12b c =⎧⎨=⎩。
所以 1sin 2ABC S bc A ∆==1sin 22ABC S bc A ∆==22.(1)n a S n n 32-= 对于任意的正整数都成立, ()13211+-=∴++n a S n n 两式相减,得()n a n a S S n n n n 3213211+-+-=-++ ∴32211--=++n n n a a a , 即321+=+n n a a()3231+=+∴+n n a a ,即11323n n n n b a b a +++==+对一切正整数都成立. ∴数列{}n b 是等比数列.由已知得 3211-=a S 即11123,3a a a =-∴=∴首项1136b a =+=,公比2=q ,162n n b -∴=⋅.1623323n n n a -∴=⋅-=⋅-.(2)323n n na n n =⨯⋅-,233(1222322)3(123),n n T n n ∴=⋅+⋅+⋅++⋅-++++ 234123(1222322)6(123),n n T n n +=⋅+⋅+⋅++⋅-++++ 2313(2222)323(123)n n n T n n +-=++++-⋅+++++2(21)3(1)362212n n n n n -+=⋅-⋅+-3(1)(66)26.2n n n n T n +∴=-⋅+-。
