建筑结构受弯构件的正截面和斜截面受弯承载力计算参考课件
合集下载
第八章受弯构件斜截面承载力计算PPT课件

2验算截面尺寸是否满要足求
因hw 440 2.2 4.0 b 200
0.25c fcbh0 261.8kNV 200kN
尺寸满足要求 71
(3)验算是否需要按计算配筋 0.7ftbh0=78.232kN<V 需要计算 (4)设只配箍筋
V0.7ftb0h1.2f5yvA ssvh0 A svV0.7ftb0h 200 7080 21 0 .0 35 2 s 1.2f5 yh v0 1.2 5 21 4040 选双肢8 ,Asv=100.6, s10.0695.8
8.4 8.4.1
36
8.4.1基本假定
1.假定梁的斜截面受剪承载力Vu由斜裂缝上剪 压区混凝土的抗剪能力Vc,与斜裂缝相交的箍筋的抗 剪能力Vsv和与斜裂缝相交的弯起钢筋的抗剪能力Vsb 三部分所组成(图5-15)。由平衡条件∑Y=0可得:
Vu= Vc +Vsv+Vsb
Vc
Vu
Vs Vsb
受剪承载力的组成
对有腹筋梁来说,只要截面尺寸合适,箍筋数量 适当,剪压破坏是斜截面受剪破坏中最常见的一种破 坏形式。
25
26
27
28
29
8.3
30
31
32
33
34
如图表示配箍率与箍 筋强度fyv的乘积对梁受剪 承载力的影响。当其它条 件相同时,两者大体成线 性关系。如前所述,剪切 破坏属脆性破坏。为了提 高斜截面的延性,不宜采 用高强度钢筋作箍筋。
箍筋的形式和构造要求
1. 箍筋的形式
单肢箍n=1 双肢箍n=2
四肢箍n=4
箍筋的形式和构造要求
2. 最小配箍率和箍筋的最大间距
最小配箍率
P
P
svmi n A bsvs0.24ft /fyv
因hw 440 2.2 4.0 b 200
0.25c fcbh0 261.8kNV 200kN
尺寸满足要求 71
(3)验算是否需要按计算配筋 0.7ftbh0=78.232kN<V 需要计算 (4)设只配箍筋
V0.7ftb0h1.2f5yvA ssvh0 A svV0.7ftb0h 200 7080 21 0 .0 35 2 s 1.2f5 yh v0 1.2 5 21 4040 选双肢8 ,Asv=100.6, s10.0695.8
8.4 8.4.1
36
8.4.1基本假定
1.假定梁的斜截面受剪承载力Vu由斜裂缝上剪 压区混凝土的抗剪能力Vc,与斜裂缝相交的箍筋的抗 剪能力Vsv和与斜裂缝相交的弯起钢筋的抗剪能力Vsb 三部分所组成(图5-15)。由平衡条件∑Y=0可得:
Vu= Vc +Vsv+Vsb
Vc
Vu
Vs Vsb
受剪承载力的组成
对有腹筋梁来说,只要截面尺寸合适,箍筋数量 适当,剪压破坏是斜截面受剪破坏中最常见的一种破 坏形式。
25
26
27
28
29
8.3
30
31
32
33
34
如图表示配箍率与箍 筋强度fyv的乘积对梁受剪 承载力的影响。当其它条 件相同时,两者大体成线 性关系。如前所述,剪切 破坏属脆性破坏。为了提 高斜截面的延性,不宜采 用高强度钢筋作箍筋。
箍筋的形式和构造要求
1. 箍筋的形式
单肢箍n=1 双肢箍n=2
四肢箍n=4
箍筋的形式和构造要求
2. 最小配箍率和箍筋的最大间距
最小配箍率
P
P
svmi n A bsvs0.24ft /fyv
第三章受弯构件正截面的承载力计算 67页PPT文档

2、梁的构造要求:
d=10~32mm(常用)
h0=h-as
单排 as= 35mm 双排 a = 50~60mm
►为保证耐久性、防火性以及钢筋 与混凝土的粘结性能,钢筋的混 凝土保护层厚度一般不小于 25mm; ►为保证混凝土浇注的密实性,梁 底 部 钢 筋 的 净 距 不 小 于 2 5 mm 及 钢 筋 直 径 d, 梁 上 部 钢 筋 的 净 距 不小于30mm及1.5 d; ►梁底部纵向受力钢筋一般不少于 2根,直径常用10~32。钢筋数量 较多时,可多排配置,也可以采 用并筋配置方式;
Teacher Chen Hong
Teacher Chen Hong
Teacher Chen Hong
主要受力特点如下表:
Teacher Chen Hong
二、钢筋砼梁正截面的破坏形式
1.适筋梁破坏:配筋量合适,破坏是受拉区的钢筋先屈服, 受压区砼被压碎而破坏,属于延性破坏。 2.超筋梁破坏:配筋量过大,特点是受压区砼边缘先压碎, 而受拉区钢筋未屈服,属于脆性破坏。 3.少筋梁破坏:配筋量过少,特点是受拉区砼一裂就坏, 属于脆性破坏。 三、界限破坏:即适筋梁和超筋梁的界限,梁破坏时受拉 区钢筋屈服的同时受压区混凝土压应变也恰好达到极限值。 此时的配筋率为界限配筋率d。
Teacher Chen Hong
3.3 单筋矩形截面梁的正截面受弯承载力计算方法
一.基本假定
1.截面应变的平截面假定。 2.不考虑混凝土的抗拉强度。 3.砼的受压应力应变图形如图5.3.1所示。
4.钢筋的应力应变关系 方程为:
图5.3.1
两个图形等效的条件: 砼压应力的合力大小相等且作 用点不变。
注:x=1xc
Teacher Chen Hong
四章受弯构件正截面承载力计算ppt课件

解:
第四章 受弯构件正截面承载力计算
1、求钢筋面积As
取 b=1000mm的板带作为计算单元;
设板厚为80mm,板自重 gk=25×0.08=2.0kN/m2 由材料强度,查附表2-2、2-7,得 fc=14.3N/mm2, ft=1.43N/mm2,
由fy=表2140-N5:/mm1=21.0,β1=0.8,由表4-6ξb=0.614。
➢ 第二阶段 —— 从截面开裂到纵向受拉钢筋屈服前阶段。
➢ 第三阶段 —— 钢筋屈服到破坏阶段。
第四章 受弯构件正截面承载力计算
各阶段和各特征点的截面应力 — 应变分析:
cu
应变图
应力图 M
t u
Mcr
M
y
My
M
xc C
Mu Z
sAs
I
ftk sAs
Ia
sAs
II
fyAs IIa
fyAs III
fyAs=T IIIa
第四章 受弯构件正截面承载力计算
截面承载力计算的两类问题
1.截面设计: 已知: bh, fc, fy, M 求: As= ?
2.截面校核:
已知: bh, fc, fy, As,M 求: Mu= ?
1. 截面设计:
第四章 受弯构件正截面承载力计算
• 由力学分析确定弯矩的设计值M
• 由跨高比确定截面初步尺寸
• 验算适用条件
m in
h h0
和x
xb (或
b )
•求Mu
• 若Mu M,则结构安全
当 < min.h/h0 取 = min.h/h0
当 x > xb Mu = Mu,max = 1 fcbh02b(1-0.5b)
建筑结构-受弯构件正截面承载力计算.ppt

❖为了传力均匀及避免结构局部破坏,板中受力钢筋的间距不
宜过大。一般条件下板中受力钢筋中心距最大值可按下面数 值控制:
h≤200mm: 250mm 200mm≤h≤1 500mm : 300mm h>1 500mm:0.2h及400mm中的小值 ( h为板的厚度)。 同时板中的钢筋间距也不宜过小(以避免施工繁杂和增大工作 量)。受力钢筋的最小间距为70mm。
混凝土结构基本原理
§5.1 概 述
5.1.2 受弯构件的类型
梁和板:截面上有弯矩和剪力,轴力可以忽略不计。 常用的截面形式如下:
主页 目录
(a)
(b)
(c)
(d)
(e)
(f )
(g)
图 5-1 建筑工程常用梁板截面形状
上一章 下一章 帮助
工程实例
梁板结构
挡土墙板 梁式桥
混凝土结构基本原理
(a)
混凝土压坏
斜截面破坏
当受弯构件沿弯矩最大截面破坏时,破坏截面与 构件的轴线垂直,称为沿正截面破坏。当受弯构 件沿剪力最大或弯矩和剪力都较大的截面破坏时, 破坏截面与构件的轴线斜交,称为沿斜截面破坏。
混凝土结构设计原理
§5.1 概 述 5.1.1几个基本概念
1.受弯构件:主要指各种类型的梁和板。 内力特点:截面上通常有弯矩和剪力共同作用。
2. 正截面:与构件计算轴线相垂直的截面。
3. 承载力计算公式: M ≤Mu
M —— 受弯构件正截面弯矩设计值; Mu——受弯构件正截面受弯承载力设计值。
主页 目录 上一章 下一章 帮助
≥30mm
1.5d c≥cmin d
h0
≥cmin
d
a
c≥cmin
d
宜过大。一般条件下板中受力钢筋中心距最大值可按下面数 值控制:
h≤200mm: 250mm 200mm≤h≤1 500mm : 300mm h>1 500mm:0.2h及400mm中的小值 ( h为板的厚度)。 同时板中的钢筋间距也不宜过小(以避免施工繁杂和增大工作 量)。受力钢筋的最小间距为70mm。
混凝土结构基本原理
§5.1 概 述
5.1.2 受弯构件的类型
梁和板:截面上有弯矩和剪力,轴力可以忽略不计。 常用的截面形式如下:
主页 目录
(a)
(b)
(c)
(d)
(e)
(f )
(g)
图 5-1 建筑工程常用梁板截面形状
上一章 下一章 帮助
工程实例
梁板结构
挡土墙板 梁式桥
混凝土结构基本原理
(a)
混凝土压坏
斜截面破坏
当受弯构件沿弯矩最大截面破坏时,破坏截面与 构件的轴线垂直,称为沿正截面破坏。当受弯构 件沿剪力最大或弯矩和剪力都较大的截面破坏时, 破坏截面与构件的轴线斜交,称为沿斜截面破坏。
混凝土结构设计原理
§5.1 概 述 5.1.1几个基本概念
1.受弯构件:主要指各种类型的梁和板。 内力特点:截面上通常有弯矩和剪力共同作用。
2. 正截面:与构件计算轴线相垂直的截面。
3. 承载力计算公式: M ≤Mu
M —— 受弯构件正截面弯矩设计值; Mu——受弯构件正截面受弯承载力设计值。
主页 目录 上一章 下一章 帮助
≥30mm
1.5d c≥cmin d
h0
≥cmin
d
a
c≥cmin
d
受弯构件斜截面承载力计算ppt

(c)斜压破坏(m≤1) 腹部开裂,几条平行斜裂缝把梁腹分割成小柱体而压碎
6
4、1、3有腹筋简支梁斜截面得受力状态
腹筋——箍筋或箍筋+弯起筋
1)有腹筋简支梁斜截面出现前后得应力状态
开裂前:腹筋作用很小
开裂后:腹筋应力增加显著;
帮助混凝土一起抗剪得能力强大?
7
2)有腹筋梁斜截面破坏得主要形态 a、斜拉破坏
3)纵向钢筋配筋率 4)配箍率与箍筋强度 此外,截面形状及尺寸对Vu得影响较大。
配箍率计算方法
sv
Asv bSv
11
大家学习辛苦了,还是要坚持
继续保持安静
思考1
1、配有腹筋梁得斜截面破坏形态有几种 ?各在什么情况下发生?
2、您认为影响梁斜截面抗剪能力得最主 要因素就是哪些?
13
4、3受弯构件得斜截面抗剪承载力
4、3、1斜截面抗剪承载力计算得基本公式
及适用条件
1)基本公式
Vu Vc Vsv Vsb Vu Vcs Vsb
Vsb (0.75) f sd Asb sin s
Vcs Vc Vsv
123 (0.45 103 )bh0 (2 0.6 p) f f cu,k sv sv
14
4、3受弯构件得斜截面抗剪承载力
2)适用条件 (1)上限值——截面最小尺寸
0Vd (0.51 103 ) f cu,k bh0 (kN) 4-6
(2)下限值——按构造要求配置箍筋条件
0Vd (0.5 103 )2 ftd bh0 (kN) 4-7
15
4、3、2 等高度简支梁腹筋得初步设计
要求:配置纵筋,弯起筋及箍筋。
截面位置 跨中截面 L/4跨截面 支座截面
弯矩kN、m 2200 1600 0
6
4、1、3有腹筋简支梁斜截面得受力状态
腹筋——箍筋或箍筋+弯起筋
1)有腹筋简支梁斜截面出现前后得应力状态
开裂前:腹筋作用很小
开裂后:腹筋应力增加显著;
帮助混凝土一起抗剪得能力强大?
7
2)有腹筋梁斜截面破坏得主要形态 a、斜拉破坏
3)纵向钢筋配筋率 4)配箍率与箍筋强度 此外,截面形状及尺寸对Vu得影响较大。
配箍率计算方法
sv
Asv bSv
11
大家学习辛苦了,还是要坚持
继续保持安静
思考1
1、配有腹筋梁得斜截面破坏形态有几种 ?各在什么情况下发生?
2、您认为影响梁斜截面抗剪能力得最主 要因素就是哪些?
13
4、3受弯构件得斜截面抗剪承载力
4、3、1斜截面抗剪承载力计算得基本公式
及适用条件
1)基本公式
Vu Vc Vsv Vsb Vu Vcs Vsb
Vsb (0.75) f sd Asb sin s
Vcs Vc Vsv
123 (0.45 103 )bh0 (2 0.6 p) f f cu,k sv sv
14
4、3受弯构件得斜截面抗剪承载力
2)适用条件 (1)上限值——截面最小尺寸
0Vd (0.51 103 ) f cu,k bh0 (kN) 4-6
(2)下限值——按构造要求配置箍筋条件
0Vd (0.5 103 )2 ftd bh0 (kN) 4-7
15
4、3、2 等高度简支梁腹筋得初步设计
要求:配置纵筋,弯起筋及箍筋。
截面位置 跨中截面 L/4跨截面 支座截面
弯矩kN、m 2200 1600 0
建筑结构受弯构件的正截面和斜截面受弯承载力计算
三.等效矩形应力图 1.问题的提出:由图(a)的方法进行计算,需 要进行积分运算,为避免之,简化计算, 欲将图(a) 换成(b)图; 2.换算对象:混凝土压应力分布图形; 3.换算原则:将曲线分布换算成矩形分布, 保持合力大小及作用点不变。 X fc ,(对相关参数进 4.换算结果: X c , 1 fc 行说明)
四. 界限相对受压区高度ξb ξb=0.8/(1+fy/0.0033Es)
适筋截面 b
界限配筋截面 b
超筋截面 b
五.适筋梁与少筋梁的界限及最小配筋率 1.确定原则:适筋梁与少筋梁破坏的界限是 裂缝一出现受拉钢筋的应力即达屈服,宣 告梁破坏。此时对应的梁的配筋率即为最 小配筋率 min 2.最小配筋率的具体取值为 max( 0.45 f f ,0.002 )
因此配置箍筋并不能减小近支座52五受弯构件斜截面承载力计算斜截面受剪承载力计算公式影响梁受剪承载力的因素无腹筋梁的受剪承载力受到很多因素的影响如剪跨比混凝土强度纵筋配筋率荷载形式集中荷载分布荷载加载方式直接加载间接加载结构类型简支梁连续梁及截面形在直接加载荷载作用于梁顶面情况下剪跨比是影响集中荷载作用下无腹筋梁抗剪强度的主要因素
1 f cbx f y As f y As
x M M u 1 f cbx(h0 ) f y As (h0 a) 2
四、双筋矩形截面受弯构件的正截 面受弯承载力计算
3.适用条件 (1) X bh0 —确保纵向受拉钢筋屈服; (2) X 2as —确保受压钢筋屈服。 三.计算方法 1.截面设计 (1)情况1:已知截面尺寸、材料等级环境 类别及弯矩,求纵向受拉和受压钢筋截面 面积。
一.概述 1.双筋截面:截面受拉和受压区均布置有纵向钢筋,且在计 算中考虑它们受力; 2.在受压区布置受力钢筋是不经济的; 3.工程中通常仅在以下情况下采用双筋截面: (1)当截面尺寸和材料强度受建筑使用和施工条件(或整 个工程)限制而不能增加,而按单筋截面计算又不满足适 筋截面条件时,可采用双筋截面,即在受压区配置钢筋以 补充混凝土受压能力的不足。 (2)由于荷载有多种组合情况,在某一组合情况下截面承 受正弯矩,另一种组合情况下承受负弯矩,这时也出现双 筋截面。 (3)由于受压钢筋可以提高截面的延性,因此,在抗震结 构中要求框架梁必须必须配置一定比例的受压钢筋。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
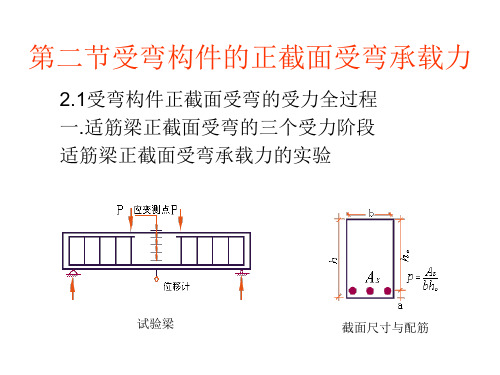
第二节受弯构件的正截面受弯承载力
2.1受弯构件正截面受弯的受力全过程 一.适筋梁正截面受弯的三个受力阶段 适筋梁正截面受弯承载力的实验
试验梁
截面尺寸与配筋
1
适筋截面:配筋率比较适当的截面; 适筋梁:具有适筋截面的梁; 实验设计:见上图 简支梁、三分点加集中力、获取纯弯段; 集中力从零逐步加至梁破坏。 实验过程分析 三阶段的划分原则: • 第Ⅰ阶段:弯矩从零到受拉区边缘混凝土
18
• (2) 选用材料、确定截面尺寸
• 采用C25级混凝土fc=13.5N/mm2,新Ⅲ级钢筋 fy=360N/mm2,αs,max=O.384
• 设h=l/14=6000/14=428.6mm,取h=450mm。按 b=(1/2~1/3)h,取b=200mm
• 初步估计纵向受拉钢筋为单排布置,ho=450-
(2)防止少筋破坏:
xbh0 或 b
As
bh0
max
b
fc
fy
As mibn h
13
14
• 4.单筋矩形截面能承担的最大弯矩为: • Mu=fbhoξb(1-0.5ξb) • 由此可看出,该最大弯矩仅与混凝土级别、
钢筋级别和截面尺寸有关,与钢筋用量无 关。 • 二.截面承载力计算的两类问题 • 1.截面设计 • 2.截面复核:
35=415mm
•
(3) 计算αs, 并验算适用条件①
• αs=M/fcbho2=120.6×106/(13.5×200×4152)=0 .259<αs,max 满足适用条件①
•
(4) 按αs计算γs
•
γs=0.5[1+(1-2αs)1/2]=0.5[1+(1-
2×0.259)1/2]=0.847
19
即将开裂,结束时称为Ⅰa阶段,其标志为 受 极拉限区拉边伸缘应混 变凝εc土u )达;到其抗拉强度ft (或其
2
• 第Ⅱ阶段:弯矩从开裂弯矩到受拉钢筋即 将屈服,结束时称为Ⅱa阶段,其标志为纵 向受拉钢筋应力达到fy;
• 第Ⅲ阶段:弯矩从屈服弯矩到受压区边缘 混凝土即将压碎,结束时称为Ⅲa阶段,其 标志为受压区边缘混凝土达到其非均匀受 压时的极限压应变εcu 。
非均匀受压时的极限压应变为0.0033,见下 图; 4.钢筋的应力-应变关系为完全弹塑性,见下图;
5
6
受压区混凝土压应力的合力及其作用点
7
三.等效矩形应力图 1.问题的提出:由图(a)的方法进行计算,需
要进行积分运算,为避免之,简化计算, 欲将图(a) 换成(b)图; 2.换算对象:混凝土压应力分布图形; 3.换算原则:将曲线分布换算成矩形分布, 保持合力大小及作用点不变。 4.换算结果: Xc ,X fc ,1fc (对相关参数进 行说明)
• 满足适用条件① • (3) 计算最大弯矩设计值M • M=fcbx(ho-
x/2)=1l×200×143.3×(416-143.3/2) • =108560000 N·mm=108.56 kN·m
17
• [例4-2] • 承受均布荷载的矩形截面简支梁,计算跨
度l=6m。永久荷载(包括梁自重)标准值 g=5kN/m,荷载分项系数1.2;可变荷载标 准值p=16kN/m,荷载分项系数1.3。试按 正截面受弯承载力确定此梁的截面尺寸、 材料强度等级及纵向受拉钢筋。 • 解: • (1) 求跨中截面弯矩设计值M
15
• [例4-1]
• 已知矩形截面梁的截面尺寸b×h =200mm×450mm,混凝土为C20级,配置4根 直径d=18mm的Ⅱ级纵向受拉钢筋,As=1017mm2。 求此梁所能承受的最大弯矩设计值。
• 解:
•
(1) 验算适用条件②
•
AS/bh=1017/(200×450)=0.0113
>ρmin=0.0015, 满足适用条件②
• (5) 计算纵向受拉钢筋截面面积AS,选配钢 筋,并验算适用条件②
• AS=M/γsfyho=120.6×106/(0.847×360× 415)=953mm2
• 选用3根直径d=20mm的新Ⅲ级纵向受拉钢 筋AS=941mm2
• AS/bh=941/(200×450)=0.0105 >ρmin,满 足适用条件②
•
(2) 计算受压区高度x,并验算适用条件①
•
ho=h-a=450-(25+பைடு நூலகம்8/2)=416mm
16
• 查表得C20级混凝土fc=9.6N/mm2,Ⅱ级钢 (d<25mm) fy=310N/mm2,ξb=0.544 x=fyAS/fcb=(310×1017)/(11×200)=143.3 mm<ξbho=0.544×416=226.3mm
3
三阶段划分的理论意义:是今后推导相关计算公式 的理论基础,例如:
Ⅰa :抗裂验算的依据; Ⅱa :裂缝宽度及变形验算的依据; Ⅲa :正截面受弯承力计算的依据 二.正截面受弯的三种破坏形态 • 破坏形态 适筋破坏 超筋破坏 少筋破坏 界限破坏
4
正截面承载力计算原理 正截面承载力计算的基本假定 1.平均应变沿截面高度线性分布(平截面假定); 2.忽略受拉区混凝土的抗拉强度; 3.混凝土受压时的应力-应变关系为曲线,混凝土
• 钢筋净间距=(200-3×202×25)/2=45mm > 25mm, 且> d=20mm, 可以。
20
T形截面受弯构件正截面受弯承载力计算
一.概述 1.考虑采用T形截面的原因: (1)根据单筋矩形截面基本计算公式可知,
10
六单筋矩形截面承载力计算 一.基本计算公式及适用条件 1. 计算简图
fc
M
x=b xn
C= fcbx
Ts=ssAs
11
2. 基本公式 根据截面受力的平衡关系,可导出单筋矩形截面受
弯承载力的计算公式:
1fcbxfyAs MMu1fcb(xh02x)fyAs(h02x)
12
3.适用条件 (1)防止超筋破坏:
8
四. 界限相对受压区高度ξb ξb=0.8/(1+fy/0.0033Es)
适 筋 截 面b
界 限 配 筋 截 面 b
超 筋 截 面b
9
五.适筋梁与少筋梁的界限及最小配筋率 1.确定原则:适筋梁与少筋梁破坏的界限是
裂缝一出现受拉钢筋的应力即达屈服,宣 告梁破坏。此时对应的梁的配筋率即为最 小配筋率 m in 2.最小配筋率的具体取值为minma0x .4(5ft fy,0.00)2
2.1受弯构件正截面受弯的受力全过程 一.适筋梁正截面受弯的三个受力阶段 适筋梁正截面受弯承载力的实验
试验梁
截面尺寸与配筋
1
适筋截面:配筋率比较适当的截面; 适筋梁:具有适筋截面的梁; 实验设计:见上图 简支梁、三分点加集中力、获取纯弯段; 集中力从零逐步加至梁破坏。 实验过程分析 三阶段的划分原则: • 第Ⅰ阶段:弯矩从零到受拉区边缘混凝土
18
• (2) 选用材料、确定截面尺寸
• 采用C25级混凝土fc=13.5N/mm2,新Ⅲ级钢筋 fy=360N/mm2,αs,max=O.384
• 设h=l/14=6000/14=428.6mm,取h=450mm。按 b=(1/2~1/3)h,取b=200mm
• 初步估计纵向受拉钢筋为单排布置,ho=450-
(2)防止少筋破坏:
xbh0 或 b
As
bh0
max
b
fc
fy
As mibn h
13
14
• 4.单筋矩形截面能承担的最大弯矩为: • Mu=fbhoξb(1-0.5ξb) • 由此可看出,该最大弯矩仅与混凝土级别、
钢筋级别和截面尺寸有关,与钢筋用量无 关。 • 二.截面承载力计算的两类问题 • 1.截面设计 • 2.截面复核:
35=415mm
•
(3) 计算αs, 并验算适用条件①
• αs=M/fcbho2=120.6×106/(13.5×200×4152)=0 .259<αs,max 满足适用条件①
•
(4) 按αs计算γs
•
γs=0.5[1+(1-2αs)1/2]=0.5[1+(1-
2×0.259)1/2]=0.847
19
即将开裂,结束时称为Ⅰa阶段,其标志为 受 极拉限区拉边伸缘应混 变凝εc土u )达;到其抗拉强度ft (或其
2
• 第Ⅱ阶段:弯矩从开裂弯矩到受拉钢筋即 将屈服,结束时称为Ⅱa阶段,其标志为纵 向受拉钢筋应力达到fy;
• 第Ⅲ阶段:弯矩从屈服弯矩到受压区边缘 混凝土即将压碎,结束时称为Ⅲa阶段,其 标志为受压区边缘混凝土达到其非均匀受 压时的极限压应变εcu 。
非均匀受压时的极限压应变为0.0033,见下 图; 4.钢筋的应力-应变关系为完全弹塑性,见下图;
5
6
受压区混凝土压应力的合力及其作用点
7
三.等效矩形应力图 1.问题的提出:由图(a)的方法进行计算,需
要进行积分运算,为避免之,简化计算, 欲将图(a) 换成(b)图; 2.换算对象:混凝土压应力分布图形; 3.换算原则:将曲线分布换算成矩形分布, 保持合力大小及作用点不变。 4.换算结果: Xc ,X fc ,1fc (对相关参数进 行说明)
• 满足适用条件① • (3) 计算最大弯矩设计值M • M=fcbx(ho-
x/2)=1l×200×143.3×(416-143.3/2) • =108560000 N·mm=108.56 kN·m
17
• [例4-2] • 承受均布荷载的矩形截面简支梁,计算跨
度l=6m。永久荷载(包括梁自重)标准值 g=5kN/m,荷载分项系数1.2;可变荷载标 准值p=16kN/m,荷载分项系数1.3。试按 正截面受弯承载力确定此梁的截面尺寸、 材料强度等级及纵向受拉钢筋。 • 解: • (1) 求跨中截面弯矩设计值M
15
• [例4-1]
• 已知矩形截面梁的截面尺寸b×h =200mm×450mm,混凝土为C20级,配置4根 直径d=18mm的Ⅱ级纵向受拉钢筋,As=1017mm2。 求此梁所能承受的最大弯矩设计值。
• 解:
•
(1) 验算适用条件②
•
AS/bh=1017/(200×450)=0.0113
>ρmin=0.0015, 满足适用条件②
• (5) 计算纵向受拉钢筋截面面积AS,选配钢 筋,并验算适用条件②
• AS=M/γsfyho=120.6×106/(0.847×360× 415)=953mm2
• 选用3根直径d=20mm的新Ⅲ级纵向受拉钢 筋AS=941mm2
• AS/bh=941/(200×450)=0.0105 >ρmin,满 足适用条件②
•
(2) 计算受压区高度x,并验算适用条件①
•
ho=h-a=450-(25+பைடு நூலகம்8/2)=416mm
16
• 查表得C20级混凝土fc=9.6N/mm2,Ⅱ级钢 (d<25mm) fy=310N/mm2,ξb=0.544 x=fyAS/fcb=(310×1017)/(11×200)=143.3 mm<ξbho=0.544×416=226.3mm
3
三阶段划分的理论意义:是今后推导相关计算公式 的理论基础,例如:
Ⅰa :抗裂验算的依据; Ⅱa :裂缝宽度及变形验算的依据; Ⅲa :正截面受弯承力计算的依据 二.正截面受弯的三种破坏形态 • 破坏形态 适筋破坏 超筋破坏 少筋破坏 界限破坏
4
正截面承载力计算原理 正截面承载力计算的基本假定 1.平均应变沿截面高度线性分布(平截面假定); 2.忽略受拉区混凝土的抗拉强度; 3.混凝土受压时的应力-应变关系为曲线,混凝土
• 钢筋净间距=(200-3×202×25)/2=45mm > 25mm, 且> d=20mm, 可以。
20
T形截面受弯构件正截面受弯承载力计算
一.概述 1.考虑采用T形截面的原因: (1)根据单筋矩形截面基本计算公式可知,
10
六单筋矩形截面承载力计算 一.基本计算公式及适用条件 1. 计算简图
fc
M
x=b xn
C= fcbx
Ts=ssAs
11
2. 基本公式 根据截面受力的平衡关系,可导出单筋矩形截面受
弯承载力的计算公式:
1fcbxfyAs MMu1fcb(xh02x)fyAs(h02x)
12
3.适用条件 (1)防止超筋破坏:
8
四. 界限相对受压区高度ξb ξb=0.8/(1+fy/0.0033Es)
适 筋 截 面b
界 限 配 筋 截 面 b
超 筋 截 面b
9
五.适筋梁与少筋梁的界限及最小配筋率 1.确定原则:适筋梁与少筋梁破坏的界限是
裂缝一出现受拉钢筋的应力即达屈服,宣 告梁破坏。此时对应的梁的配筋率即为最 小配筋率 m in 2.最小配筋率的具体取值为minma0x .4(5ft fy,0.00)2
