龙贝格积分 python
计算方法大作业——龙贝格积分

3 龙贝格积分3.1 算法原理及程序框图龙贝格积分法是在复化梯形求积公式、复化辛普森求积公式和复化科茨求积公式关系的基础上,构造出的一种精度更高的数值积分方法。
对于复化梯形求积公式而言,近似积分为()2221[]41n n n n I f T T T T ≈+-=-.(11) 对于复化辛普森求积公式和复化科茨求积公式而言,也有类似的关系,如公式(12)和公式(13)。
()22221[]41n n n n I f S S S S ≈+-=- (12)()22231[]41n n n n I f C C C C ≈+-=- (13)通过对公式(11)~(13)做进一步分析,可得到公式(14)和公式(15)。
()22141n n n n S T T T =+--(14)()222141n n n n C S S S =+-- (15)根据公式(14)和公式(15)表现出来的规律,令龙贝格积分为()223141n n n n R C C C =+-- (16)其截断误差为c R h 8f (8)(η),已经具有很高的精度。
龙贝格积分法是将区间[a , b ]逐次分半进行计算,因此,对已知函数f (x )在区间[a , b ]上的龙贝格积分法的计算公式的算法如下,程序框图如图13所示。
(1) 计算T 1:[]1()()2b aT f a f b -=+;(2) 逐次计算T 2k +1:()1211221121,0,1,2222kk k k k i b a b a T T f a i k +++=--⎛⎫=++-= ⎪⎝⎭∑;(3) 逐次计算S 2k 、C 2k 和R 2k :()()()11111122222222232222141141141kk k k k k k k k k k k S T T T C S S S R C C C ++++++⎧=+-⎪-⎪⎪=+-⎨-⎪⎪=+-⎪-⎩;(4) 若122k k R R ε+-<,则取[]12k I f R +≈;否则,继续计算,直到满足精度为止。
python积分语句

python积分语句Python是一种功能强大、简洁易读的编程语言,它提供了许多用于数学计算的库和函数。
其中,积分是数学中重要的概念之一,用于求解函数的面积、曲线的弯曲程度等问题。
在Python中,我们可以使用不同的库和函数来实现积分运算。
以下是我整理的10个Python积分语句的例子,希望对您有所帮助。
1. 使用scipy库中的quad函数进行积分计算:```from scipy import integratedef f(x):return x**2result, error = integrate.quad(f, 0, 1)print(result)```这段代码使用quad函数计算了函数f(x)在0到1之间的积分,并将结果打印出来。
2. 使用numpy库中的trapz函数进行梯形法积分计算:```import numpy as npx = np.linspace(0, 1, 100)y = x**2result = np.trapz(y, x)print(result)```这段代码使用梯形法计算了函数f(x)在0到1之间的积分,并将结果打印出来。
3. 使用sympy库进行符号积分计算:```import sympy as spx = sp.symbols('x')f = x**2integral = sp.integrate(f, x)print(integral)```这段代码使用sympy库进行符号积分计算,将f(x)的积分表达式打印出来。
4. 使用scipy库中的simps函数进行辛普森法积分计算:```from scipy import integratex = np.linspace(0, 1, 100)y = x**2result = integrate.simps(y, x)print(result)```这段代码使用辛普森法计算了函数f(x)在0到1之间的积分,并将结果打印出来。
龙贝格算法

龙贝格积分1. 算法原理采用复化求积公式计算时,为使截断误差不超过ε,需要估计被积函数高阶导数的最大值,从而确定把积分区间[]b a ,分成等长子区间的个数n 。
首先在整个区间[]b a ,上应用梯形公式,算出积分近似值T1;然后将[]b a ,分半,对 应用复化梯形公式算出T2;再将每个小区间分半,一般地,每次总是在前一次的基础上再将小区间分半,然后利用递推公式进行计算,直至相邻两个值之差小于允许误差为止。
实际计算中,常用ε≤-n n T T 2作为判别计算终止的条件。
若满足,则取n T f I 2][≈;否则将区间再分半进行计算,知道满足精度要求为止。
又经过推导可知,∑=-++=ni i i n n x x f h T T 112)2(221,在实际计算中,取kn 2=,则k a b h 2-=,112)1*2(2++--+=+k i i ab i a x x 。
所以,上式可以写为∑=++--+-+=+kk i k k ab i a f a b T T 211122)2)12((2211k开始计算时,取())()(21b f a f ab T +-=龙贝格算法是由递推算法得来的。
由梯形公式得出辛普森公式得出柯特斯公式最后得到龙贝格公式。
根据梯形法的误差公式,积分值n T 的截断误差大致与2h 成正比,因此步长减半后误差将减至四分之一,即有21114n n T T -≈-将上式移项整理,知2211()3n n n T T T -≈-由此可见,只要二分前后两个积分值n T 和2n T 相当接近,就可以保证计算保证结果计算结果2n T 的误差很小,这种直接用计算结果来估计误差的方法称作误差的事后估计法。
按上式,积分值2n T 的误差大致等于21()3n n T T -,如果用这个误差值作为2n T 的一种补偿,可以期望,所得的()222141333n n n n n T T T T T T =+-=-应当是更好的结果。
计算机数学软件Maple概述

控制系统分析与设计
系统建模
Maple可用于建立控制系统的数学模型,包括传递函数、状态 空间表示和频率响应等。它支持控制系统的时域和频域分析。
稳定性分析
Maple提供了多种稳定性分析方法,如劳斯判据、奈奎斯特图和根轨 迹等。它可用于评估控制系统的稳定性,并指导控制器的设计。
控制器设计
Maple支持多种控制器设计方法,如PID控制、最优控制和鲁棒控制等。 它可以帮助工程师设计高效且稳定的控制系统,以满足不同的工程需求。
控制结构
Maple提供条件语句(如if-else)、 循环语句(如for、while)等控制结 构,用于实现复杂的逻辑功能。
函数定义与调用
用户可以自定义函数,并在程序中调 用这些函数。函数可以接受参数,并 返回计算结果。
03
Maple在数学计算中的应用
符号计算
代数运算
Maple可以进行各种代数运算,如多项式运算、因式分解、求根 等。
方面更具优势。此外,Maple的编程语言相对更简单易用。
03
与Python的比较
Python是一种通用编程语言,通过安装额外的库(如NumPy、SciPy
等)可以实现数学计算功能。然而,与Maple相比,Python在符号计
算和图形可视化方面功能相对较弱。
02
Maple基础知识
Maple的界面Maple与MATLAB之间的数据交换和算 法调用。
与其他科学计算软件的接口
如与Mathematica、SageMath等软件的互 操作性。
Maple在科研与教学中的应用案例
数学研究
用于解决复杂数学问题,如微分方程求解、符号积分等。
物理工程
在物理模拟、工程设计等领域进行数学建模和仿真。
计算方法用龙贝格程序计算数值积分的值(附程序代码)

2第二题 求数值积分11sin 3sin x dx x x -+⎰精确到610-。
龙贝格的算法思想:Romberg 方法也称为逐次分半加速法。
它是在复化梯形公式的基础上,利用Richardson 外推法,构造出一种高精度的数值积分方法。
在等距基点的情况下,用计算机计算积分值通常都采用把区间逐次分半的方法进行。
这样,前一次分割得到的函数值在分半以后仍可被利用,且易于编程 。
2.2.1程序设计关键步骤(1)准备初值aa[0][0]=(b-a)*(F(a)+F(b))/2.0来实现就算初值。
(2)用 for ( n=i,j=1; n>0;n--,j++)aa[j][n]=(pf(2*j+1)*aa[j-1][n+1]-aa[j-1][n])/(pf(j*2+1)-1) 来实现(2)(k )00T T 到的计算。
(3)用fabs(aa[i][1]-aa[i][0])判断数值的精度,如果fabs(aa[i][1]-aa[i][0]<e,则返回gcc(a,b,aa,i+1)进行计算下一个要用到得值; 如果fabs(aa[i][1]-aa[i][0]> e ,则根据aa[i+1][0]=(pf(2*i+3)*aa[i][1]-aa[i][0])/(pf(2*i+3)-1)而得到结果。
2.2.2程序运行结果如下图所示#include "stdafx.h"#include <iostream>#include <math.h>#define F(x) (sin(x)/(3*x+sin(x))) //函数举例。
using namespace std;//------------步长及4,16,64.......的实现----------double pf (int i){int s=1;for (int j=0;j<i;j++)s*=2;return s/2;}//---------定义一个求t1,t2......的函数-------------double gcc (double a, double b,double aa[][20],int i){double s,h,x;h=(b-a)/pf(i);s=0;x=a+h/3;do{s+=F(x);x+=h;}while (x<b);aa[0][i]=aa[0][i-1]/2+h/2*s;return 0;}//----------------------主函数---------------------------int main(){double aa[20][20]={0},e,a,b,h;int j,i,n;cout <<"请输入积分区间:\na= ";cin >>a;cout <<"b= ";cin >>b;cout <<"请输入精度:e=";cin >>e;aa[0][0]=(b-a)*(F(a)+F(b))/2.0;gcc(a,b,aa,1);aa[1][0]=(4*aa[0][1]-aa[0][0])/3;for (i=1;i<20;i++){gcc(a,b,aa,i+1);//求下一个要用的t。
龙贝格算法求数值积分程序说明及流程图
f=1;
else
f=sin(x)/x;
end
%龙贝格算法求数值积分
clc;clear all;
flag=zeros(1,4);
In=zeros(25,4);
eps1=input('what precision do you want to get?');
i=0;
%计算一些初始序列
while(flag(4)<2)
for k=flag(1)+1:i+4
for j=1:2^(k-1)
In(k,1)=In(k,1)+sin1(a+(2*j-1)*(b-a)/(2^k));
end
if k>1
In(k,1)=In(k,1)/2^k+In(k-1,1)/2;
else
In(k,1)=(b-a)*(sin1(b)+sin1(a))/2;
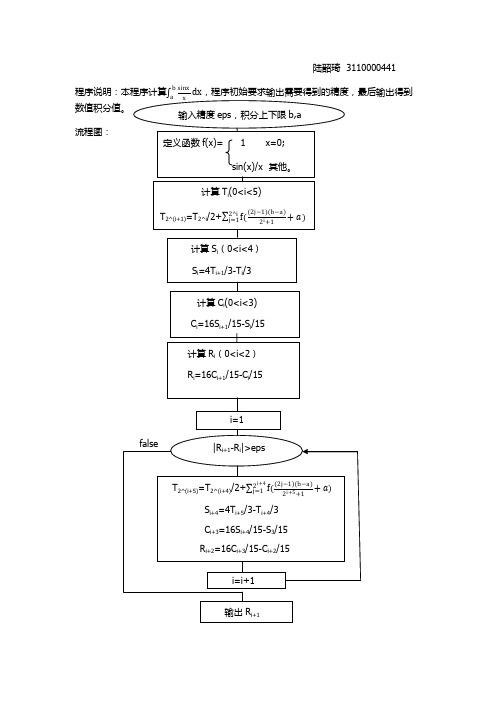
本程序计算sinx程序初始要求输出需要得到的精度最后输出得到数值积分值
陆韶琦 3110000441
程序说明:本程序计算
数值积分值。
b sinx
a x
dx,程序初始要求输出需要得到的精度,最后输出得到
输入精度 eps,积分上下限 b,a
流程图:
定义函数 f(x)=
1
x=0;
sin(x)/x 其他。
计算 Ti(0<i<5)
end
In(i+5,1)=In(i+5,1)/2^(i+5)+In(i+4,1)/2;
In(i+4,2)=4*In(i+5,1)/3-In(i+4,1)/3;
龙贝格求积公式
Romberg积分公式正是由此思想产生 积分公式正是由此思想产生
类似于梯形加速公式的处理方法,得到: 类似于梯形加速公式的处理方法,得到: 加速公式的处理方法
2 1 4 S2 n − Sn I ≈ S2 n + 2 ( S2 n − Sn ) = 2 4 −1 4 −1 2 4 S2 n − Sn Simpson加速公式: C n = 加速公式 加速公式: 2 4 −1 3 1 4 C2n − Cn I ≈ C 2 n + 3 (C 2 n − C n ) = 3 4 −1 4 −1
求出f(1/4)
f(3/4) 进而求得
T4=1/2{T2+1/2[f(1/4)+f(3/4)]} =3.131176471 S2=1/3(4T4-T2)=3.141568628 C1=1/15(16S2-S1)=3.142117648 计算f(1/8) f(3/8) f(5/8) f(7/8)进而求得 T8=1/2{T4+1/4[f(1/8)+f(3/8)+f(5/8)+f(7/8)]} =3.138988495 S4=1/3(4T3-T4)=3.141592503 C2=1/15(16S4-S2)=3.141594095 R1=1/63(64C2-C1)=3.141585784
梯形值序列
4个积分值序列: 个积分值序列: 个积分值序列
T2k
S 2k =
C 2k =
4T2k +1 − T2k 4 −1 2 4 S2k +1 − S2k
4 −1
2
2k
2k 2k
R2k =
4 C 2k +1 − C 2k
3
4 −1
3
龙贝格积分算法实验
实验题目2 Romberg 积分法摘要考虑积分()()b aI f f x dx =⎰欲求其近似值,可以采用如下公式: (复化)梯形公式 11[()()]2n ii i hT f x f x-+==+∑2()12b a E h f η-''=-[,]a b η∈ (复化)辛卜生公式 11102[()4()()]6n i i i i hS f x f x f x -++==++∑4(4)()1802b a h E f η-⎛⎫=- ⎪⎝⎭ [,]a b η∈ (复化)柯特斯公式 111042[7()32()12()90n i i i i hC f x f x f x -++==+++∑31432()7()]i i f xf x +++6(6)2()()9454b a h E f η-⎛⎫=- ⎪⎝⎭[,]a b η∈ 这里,梯形公式显得算法简单,具有如下递推关系121021()22n n n i i h T T f x -+==+∑因此,很容易实现从低阶的计算结果推算出高阶的近似值,而只需要花费较少的附加函数计算。
但是,由于梯形公式收敛阶较低,收敛速度缓慢。
所以,如何提高收敛速度,自然是人们极为关心的课题。
为此,记0,k T 为将区间[,]a b 进行2k等份的复化梯形积分结果,1,k T 为将区间[,]a b 进行2k等份的复化辛卜生积分结果,2,k T 为将区间[,]a b 进行2k等份的复化柯特斯积分结果。
根据李查逊(Richardson )外推加速方法,可得到1,11,,0,1,2,40,1,2,41m m k m km k m k T T T m -+-=-⎛⎫=⎪=-⎝⎭可以证明,如果()f x 充分光滑,则有,lim ()m k k T I f →∞= (m 固定),0lim ()m m T I f →∞=这是一个收敛速度更快的一个数值求积公式,我们称为龙贝格积分法。
工程数值计算Python教程
精彩摘录
作者介绍了Python的并行和分布式计算能力。通过使用如multiprocessing、 joblib等库,工程师可以利用多核CPU或分布式计算资源来加速数值计算过程。 这对于处理大规模、复杂的数据集或进行高性能计算具有重要的意义。
精彩摘录
《工程数值计算Python教程》这本书为工程师提供了一个全面而深入的视角 来了解如何使用Python进行工程数值计算。通过书中的精彩摘录,我们可以看到 Python在工程领域中的广泛应用和强大功能。我相信这本书对于想要提高自己在 工程数值计算方面技能的人来说是一本非常有价值的参考书籍。
目录分析
该章节介绍了数值微分和数值积分的基本原理和方法,包括复合梯形法、复 合辛普森法等数值微分方法和龙贝格积分等数值积分方法。这些方法在科学计算 中有着广泛的应用。
目录分析
该章节介绍了常微分方程组的数值解法的基本原理和方法,包括欧拉法、龙 格-库塔法等。这些方法在物理、生物、经济等领域中有着广泛的应用。
精彩摘录
作者在书的开篇就提到,Python是一种“胶水”语言,它的灵活性使得工程 师可以在其上轻松地实现各种复杂的数值计算。Python可以轻松地与其他语言进 行集成,这使得工程师可以充分利用现有的各种资源。
精彩摘录
在介绍Python的数值计算库时,作者特别强调了NumPy和Pandas的重要性。 NumPy是Python中用于科学计算的基础包,它提供了大量的数学函数和高效的数 组操作。Pandas则是一个强大的数据分析工具,它可以让工程师轻松地处理和分 析大规模的数据集。
目录分析
该章节介绍了数值积分和微分方程的基本原理和方法,包括梯形法、辛普森 法、龙贝格积分等数值积分方法以及欧拉法、龙格-库塔法等数值求解微分方程 的方法。这些方法在工程数值计算中有着广泛的应用。
python格点数据二重积分计算
在 Python 中进行格点数据的二重积分计算通常涉及到使用数值积分方法,例如采用 SciPy 库的quad函数。
假设你有一个二维函数f(x,y),需要在给定的格点上进行二重积分,以下是一个详细的解答:
在上述代码中,my_function是你要进行积分的目标函数。
在这个例子中,函数是
f(x,y)=x2+y2。
dblquad函数用于执行二重积分,其参数为目标函数、第一个变量的下限和上限、第二个变量的下限和上限。
在这个例子中,积分区域是[0,1]范围内的正方形。
请根据实际问题和数据结构修改代码。
如果格点数据以 NumPy 数组的形式给出,你可能需要对数组进行插值,然后再进行积分。
这可以使用scipy.interpolate模块中的函数来实现。
如果有特殊的网格结构,可能需要编写一个自定义的积分函数来适应数据。
总的来说,SciPy 库是一个强大的数值计算库,提供了许多用于积分、插值和其他数学计算的工具。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
龙贝格积分 python
龙贝格积分 python
一、什么是龙贝格积分?
龙贝格积分(Romberg integration)是一种数值积分方法,它是对梯形法的递推加速处理。
梯形法是一种比较简单的数值积分方法,但它的精度不高,而且需要很多次计算。
龙贝格积分通过递推计算,可以大大提高计算精度,并且减少计算次数。
二、如何实现龙贝格积分?
在 Python 中实现龙贝格积分可以使用以下代码:
```python
def romberg(f, a, b, n):
"""Calculate the Romberg Integration of f(x) from a to b with n iterations"""
R = [[0] * (n+1) for _ in range(n+1)]
h = b - a
R[0][0] = 0.5 * h * (f(a) + f(b))
for i in range(1, n+1):
h = 0.5 * h
sum = 0
for k in range(1, 2**i, 2):
sum += f(a + k*h)
R[i][0] = 0.5 * R[i-1][0] + sum*h
for j in range(1, i+1):
R[i][j] = (4**j*R[i][j-1] - R[i-1][j-1]) / (4**j - 1)
return R[n][n]
```
三、代码解析
1. 定义函数 romberg(f, a, b, n),其中 f 为被积函数,a 和 b 分别为
积分上下限,n 为迭代次数。
2. 创建一个n+1 行n+1 列的二维数组R,用于存储递推计算的结果。
3. 计算初始值 R[0][0],即使用梯形法计算第一次迭代的结果。
4. 进行 n 次迭代,每次将步长 h 减半,并且计算新的递推值。
具体过程如下:
a. 计算当前步长 h。
b. 计算当前迭代中需要累加的所有 f(x) 的和。
c. 根据梯形法公式和递推公式计算新的递推值,并存储在二维数组R 中。
5. 返回最终结果 R[n][n]。
四、代码测试
我们可以使用以下代码测试 romberg 函数:
```python
import math
def f(x):
return math.sin(x)
a = 0
b = math.pi/2
n = 10
result = romberg(f, a, b, n)
print(result)
```
该函数计算 sin(x) 在 [0, pi/2] 区间上的积分,并输出结果。
运行结果如下:
```
1.0000000000013626
```
可以看到,该函数计算出了较为精确的积分值。
五、总结
龙贝格积分是一种递推加速处理的数值积分方法,可以大大提高计算精度,并且减少计算次数。
在 Python 中,我们可以使用递推公式来实现龙贝格积分,从而得到较为精确的积分值。
