传递过程原理作业题解(1-7章)
化工原理第四章传热过程超详细讲解

例4-12 在其他条件(K,Cp,M1,M2)不变时, 并→逆,求T2, t1。 解:利用并流求得有关常数: Φ=KAΔtm=-M1Cp1ΔT’=M2Cp2Δt’
设热阻集中在保温层:则
则一米管年损失的热量:
W=J/s
年损失的价值:
一米管道耗保温材料体积:V= ∴年折旧费用:
总费用: 求导,求极值:
28.356
复杂系数一元三次方程,用试差法求解:
设D=0.4 时,左=62.8≈右=63 ∴δ=D-0.1/2=(0.4-0.1)/2=0.15 m
作业:P142 (4、5)
∴ A (t1 t 2) At
R=δ/λ—热阻
2 多层平面壁,如耐火砖——绝热砖——建筑砖组成三层复合 壁,对各层分别应用单层导热公式有:
一层:
(1)
二层:
(2)
三层:
(3)
∵平面壁:A1=A2=A3=A ∵稳定传热Φ1=Φ2=Φ3=Φ则有:
t1-t4=Δt=
…(4)
…(5)
讨论:(1) ①+②得:
(4)潜热 Q潜 mH m nH n
(J/mol*K)
式中:ΔHm和ΔHn分别为质量和摩尔相变潜热 (单位分别为: J/kg;J/mol)
§2 传导传热(热传导,导热) 一、定义:传导传热——发生在固体、静止或滞流流体中,因分
子的振动或自由电子的运动而传递热量的方式。
二、导热方程—付立叶定律:
故将对流传热扩展为:对流给热——流体与壁面 之间的传热。由于壁面附近的流体为滞流,因此:对 流给热包括湍流主体的对流传热和壁附近滞流层的热 传导,为描述此复杂的给热过程的速率,特提出对流 给热机理(模型),其要点为:
a.湍流主体以对流方式传热,温度一致, 即忽略湍流主体的热阻。
通信原理思考题及作业解答

思考题作业题解答1–11 衡量数字通信系统有效性和可靠性的性能指标有哪些?答:衡量数字通信系统有效性的性能指标有:码元传输速率R B 、信息传输速率R b 、频带利用率η。
衡量数字通信系统可靠性的性能指标有:误码率P e 和误信(比特)率P b 。
1–12 何谓码元速率和信息速率?它们之间的关系如何?答:码元速率R B 是指单位时间(每秒)传送码元的数目,单位为波特(Baud ,B )。
信息速率R b 是指单位时间内传递的平均信息量或比特数,单位为比特/秒(b/s 或bps )。
码元速率和信息速率的关系: 或 其中 M 为M 进制(M =2 k ,k = 1, 2, 3, …)。
1–13 何谓误码率和误信率?它们之间的关系如何?答:误码率P e 是指错误接收的码元数在传输总码元数中所占的比例。
误信率P b 是指错误接收的比特数在传输总比特数中所占的比例。
在二进制中有:P e =P b 。
第1章 绪论( 习题 )1–4 一个由字母A 、B 、C 、D 组成的字,对于传输的每一个字母用二进制脉冲编码:00代替A ,01代替B ,10代替C ,11代替D ,每个脉冲宽度为5ms 。
(1) 不同的字母是等可能出现时,试计算传输的平均信息速率;(2) 若每个字母出现的可能性分别为P A =1/5,P B =1/4,P C =1/4,P D =3/10,试计算传输的平均信息速率。
解:(1) 平均每个字母携带的信息量,即熵为2(比特/符号)每个字母(符号)为两个脉冲,其宽度为2×5 ms =10-2(s )则平均信息速率为:2(比特/符号)/10-2(秒/符号)=200(b/s )(2) 平均信息量为985.1310log 1034log 4125log 51)(222=⨯+⨯⨯+⨯=x H (比特/符号) 平均信息速率为:H (x )/10-2=1.985/10-2=198.5(b/s )1–7 设一数字传输系统传送二进制码元的速率为2400 B ,试求该系统的信息速率。
过程控制技术课后作业答案详解
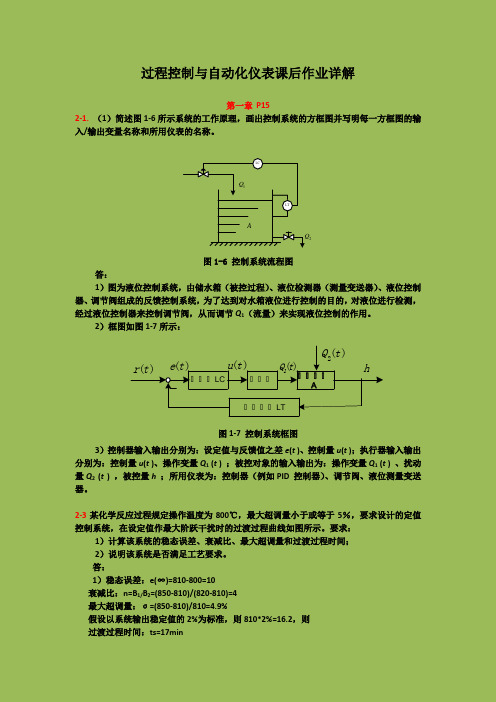
过程控制与自动化仪表课后作业详解第一章 P152-1. (1)简述图1-6所示系统的工作原理,画出控制系统的方框图并写明每一方框图的输入/输出变量名称和所用仪表的名称。
LTLC1Q 2Q A图1-6 控制系统流程图答:1)图为液位控制系统,由储水箱(被控过程)、液位检测器(测量变送器)、液位控制器、调节阀组成的反馈控制系统,为了达到对水箱液位进行控制的目的,对液位进行检测,经过液位控制器来控制调节阀,从而调节Q 1(流量)来实现液位控制的作用。
2)框图如图1-7所示:控控控LC控控控控控控控A控控控控LT_2()Q t ()1Q t ()r t ()e t ()u t h图1-7 控制系统框图3)控制器输入输出分别为:设定值与反馈值之差e (t )、控制量u (t );执行器输入输出分别为:控制量u (t )、操作变量Q 1 (t ) ;被控对象的输入输出为:操作变量Q 1 (t ) 、扰动量Q 2 (t ) ,被控量h ;所用仪表为:控制器(例如PID 控制器)、调节阀、液位测量变送器。
2-3某化学反应过程规定操作温度为800℃,最大超调量小于或等于5%,要求设计的定值控制系统,在设定值作最大阶跃干扰时的过渡过程曲线如图所示。
要求:1)计算该系统的稳态误差、衰减比、最大超调量和过渡过程时间; 2)说明该系统是否满足工艺要求。
答:1)稳态误差:e(∞)=810-800=10衰减比:n=B 1/B 2=(850-810)/(820-810)=4 最大超调量:σ=(850-810)/810=4.9%假设以系统输出稳定值的2%为标准,则810*2%=16.2,则 过渡过程时间:ts=17min2)由于规定操作温度为800︒C ,而系统稳态值为810︒C 所以不满足工艺要求。
第二章P711-3 某台测温仪表测量的上下限为500℃~1000℃,它的最大绝对误差为±2℃,试确定该仪表的精度等级;答:根据题意可知:最大绝对误差为±2℃则精度等级%4.0%1005002±=⨯±=δ 所以仪表精度等级为0.4级1-4某台测温仪表测量的上下限为100℃~1000℃,工艺要求该仪表指示值的误差不得超过±2℃,应选精度等级为多少的仪表才能满足工艺要求?答:由题可得:%22.0%10010010002±=⨯-±=δ仪表精度等级至少0.2以上。
化工传递过程基础(第三版)习题答案详解_部分1

搅拌良好,任何 θ 瞬时
(1) (2)
(3) (4) (5)
aA2 = aA
试求放出 1m3 水所需的时间。又若槽中装满煤油,其他条件不变,放出 1 m3 煤油所需时间有 何变化?设水的密度为 1000 kg/m3;煤油的密度为 800 kg/m3。
解:设槽面积为 A,孔面积为 A0,原盛水的高度为 z0,放水后的高度为 z1
则
z0=3m
z1= 3 −1
( π ×12 ) = 1.727m 4
w1 = 100kg/min, aA1 = 0.002
θ = θ 瞬时:
w2 = 60kg/min, aA2 = aA
θ = θ2 时,
aA2 = 0.01 ,求θ2 。
对组分 A 进行总质量衡算:
w2 aA 2
−
w1aA1
+
d(MaA dθ
)
=
0
上式展开:
w2 aA 2
− w1aA1 + M
daA dθ
对组分 A 作质量衡算:
w2 aA 2
−
w1aA1
+
d(MaA ) dθ
=
0
w2 aA 2
+
M
d(aA ) dθ
=
0
∫ ∫ αA daA = − w2 10 dθ
0.05 aA
M0
ln aA = − 100 ×10 = −1 0.05 1000
aA = 0.05 × e−1 = 0.0184 = 1.84%
化工传递过程基础·习题详解
(第三版)
陈涛 张国亮 主编
目录
第一章 传递过程概论 ................................................................................................1 第二章 动量传递概论与动量传递微分方程........................................................... 11 第三章 动量传递方程的若干解 ..............................................................................19 第四章 边界层流动 ..................................................................................................37 第五章 湍流 ..............................................................................................................48 第六章 热量传递概论与能量方程 ..........................................................................64 第七章 热传导 ..........................................................................................................69 第八章 对流传热 ......................................................................................................81 第九章 质量传递概论与传质微分方程.................................................................105 第十章 分子传质(扩散) .................................................................................... 113 第十一章 对流传质 ................................................................................................122 第十二章 多种传递同时进行的过程 ....................................................................133
第7章 传热过程的分析和计算

Rk
1
d1lh1
1
21l
ln
d2 d1
1
2xl
ln
dx d2
1
dxlh2
dRk ddx
1
2x d x
1
d
2 x
h2
0
dc
2x
h2
临界绝缘直径与保温材料有关、与所处环境有关
dc
2x
h2
(1)当dx<dc时,随保温层厚度的增加,总热阻 减小,传热量增大,此时对管道敷设保温层反而
7.4.2 换热器热计算的基本方程
约定: 下标 1 —— 热流体 下标 2 —— 冷流体 上标 ’ —— 进口参数 上标 ’’ —— 出口参数 以热流体进口作为计算起点
1 换热器中流体的温度分布 因变量—冷、热流体的温度 自变量—?
换热面积 —热流体入口,Ax=0 —热流体出口,Ax=At —在换热器内的不同位置,Ax不同,流体温
★如何提高传热系数?
1
1
K
1 h1
1 h2
1 h1
1 h2
数学上可以证明
K min h1, h2
提高较小的表面传热系数值,强化薄弱环节, 效果最好
h1=103,h2=10,没有强化前:K=9.90 W/(m2.K)
❖ 措施1: h1=2000,h2=10: K’=9.95 W/(m2.K)
7.2.1 通过平壁的传热过程 导热中—只关注平板的导热过程,计算了各类边
界条件下的温度分布、通过平板的导热量 传热过程中—壁面两侧流体间的热量传递过程
1 h1 A(t f 1 tW1)
2
过程控制作业答案分解

作 业第二章:2-6某水槽如题图2-1所示。
其中A 1为槽的截面积,R 1、R 2均为线性水阻,Q i 为流入量,Q 1和Q 2为流出量要求:(1)写出以水位h 1为输出量,Q i 为输入量的对象动态方程;(2)写出对象的传递函数G(s)并指出其增益K 和时间常数T 的数值。
图2-1解:1)平衡状态: 02010Q Q Q i +=2)当非平衡时: i i i Q Q Q ∆+=0;1011Q Q Q ∆+=;2022Q Q Q ∆+= 质量守恒:211Q Q Q dthd A i ∆-∆-∆=∆ 对应每个阀门,线性水阻:11R h Q ∆=∆;22R h Q ∆=∆ 动态方程:i Q R hR h dt h d A ∆=∆+∆+∆2113) 传递函数:)()()11(211s Q s H R R S A i =++ 1)11(1)()()(211+=++==Ts KR R S A s Q s H s G i2Q11这里:21121212111111R R A T R R R R R R K +=+=+=;2-7建立三容体系统h 3与控制量u 之间的动态方程和传递数,见题图2-2。
解:如图为三个单链单容对像模型。
被控参考△h 3的动态方程: 3233Q Q dth d c ∆-∆=∆;22R h Q ∆=∆;33R hQ ∆=∆; 2122Q Q dth d c ∆-∆=∆;11R h Q ∆=∆ 111Q Q dth d c i ∆-∆=∆ u K Q i ∆=∆ 得多容体动态方程:uKR h dth d c R c R c R dt h d c c R R c c R R c c R R dt h d c c c R R R ∆=∆+∆+++∆+++∆333332211232313132322121333321321)()(传递函数:322133)()()(a s a s a s Ks U s H s G +++==; 这里:32132133213213321321332211232132131313232212111;c c c R R R kR K c c c R R R a c c c R R R c R c R c R a c c c R R R c c R R c c R R c c R R a ==++=++=2-8已知题图2-3中气罐的容积为V ,入口处气体压力,P 1和气罐 内气体温度T均为常数。
热量传递篇--传热原理.

主要内容
一. 传热概述
1.传热过程
2.传热速率
二. 热传导
1. 傅立叶定律和导热系数 2. 一维稳态导热
三. 本讲小结
作业:习题19-1,19-3
一.传热概述
热力学第二定律指出,凡是有温度差存在的 地方,就必然有热量传递,故在几乎所有的 工业部门,如化工、能源、冶金、机械、建 筑等都涉及传热问题。 物料的预热和冷却 合理利用能源 可持续发展 减少热损失 煤与石油
115
1.16
125
0.11670来自0.350设T2、T3分别为耐火砖与硅藻土砖的界面温度、硅藻 土砖和石棉水泥砖的界面温度。依题意,知道热损失 即为由炉墙内向炉墙外的传热量,有: T1 Tn 1 495 60 q n 316 W / m 2 1137kJ /(m 2 h) 0.115 0.125 0.070 bi 1.16 0.116 0.350 i i 1
边界条件: x=0, t=T1 ; x=b, t=T2
T1 T2 T1 T2 Q A b b ( A)
传导距离越大,传 热面积和导热系数 越小,热阻越大。
2) 通过多层平壁的稳态热传导
T1 T2 T1 T2 Q 1 A b1 b1 (1 A) T2 T3 T2 T3 2 A b2 b2 (2 A)
推广到通过n层平壁的稳态热传导,
T1 Tn 1 Q n bi (i A) i 1 T1 Tn 1 q n bi
i 1
i
例题:锅炉炉墙由耐火砖、硅藻土砖和石棉水泥砖三层组 成,各层的厚度、导热系数由下表所示,炉墙内外表面的 温度分别为495℃ 和60℃ ,试求每平方米炉墙每小时的热 损失及各层界面上的温度。 耐火砖 厚度(mm) 导热系数 (w/(m2· K)) 解: 硅藻土砖 石棉水泥砖
《传递过程原理》课后习题参考答案

《传递过程原理》课程第一次作业参考答案(P56)1. 不可压缩流体绕一圆柱体作二维流动,其流场可用下式表示θθθsin ;cos 22⎪⎪⎭⎫⎝⎛+=⎪⎪⎭⎫⎝⎛-=D r C u D r C u r其中C ,D 为常数,说明此时是否满足连续方程。
2. 判断以下流动是否可能是不可压缩流动(1) ⎪⎩⎪⎨⎧-+=--=++=zx t u z y t u yx t u z y x 222 (2) ()()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=-==-=22221211t tz u xy u x y u z y x ρρρρ3.对于下述各种运动情况,试采用适当坐标系的一般化连续性方程描述,并结合下述具体条件将一般化连续性方程加以简化,指出简化过程的依据。
(1)在矩形截面流道内,可压缩流体作定态一维流动;(2)在平板壁面上不可压缩流体作定态二维流动;(3)在平板壁面上可压缩流体作定态二维流动;(4)不可压缩流体在圆管中作轴对称的轴向定态流动;(5)不可压缩流体作圆心对称的径向定态流动。
《化工传递过程导论》课程作业第三次作业参考P-573-1流体在两块无限大平板间作定态一维层流,求截面上等于主体速度u b的点距离壁面的距离。
又如流体在圆管内作定态一维层流,该点距离壁面的距离为若干?距离壁面的距离02(12d r =-3-2温度为20℃的甘油以10kg/s 的质量流率流过长度为1m ,宽度为0.1m 矩形截面管道,流动已充分发展。
已知20℃时甘油的密度ρ=1261kg/m 3,黏度μ=1.499Pa·s 。
试求算(1)甘油在流道中心处的流速以及距离中心25mm 处的流速; (2)通过单位管长的压强降;2max 012P u y xμ∂=-∂流动方向上的压力梯度Px∂∂的表达式为:max 22u Px y μ∂=-∂ 所考察的流道为直流管道,故上式可直接用于计算单位管长流动阻力:fP L∆,故: -1max 22022 1.4990.119142.7Pa m 0.1()2f P u P P L x L y μ∆∂∆⨯⨯=-=-===⋅∂ (3) 管壁处剪应力为:2max max 002[(1())]xy y y yu u yu yy y y μτμτμ==∂∂=-⇒=--=∂∂ max 2022 1.4990.119N 7.135m 0.12u y μτ⨯⨯⇒===故得到管壁处的剪应力为2N7.135m《化工传递过程导论》课程第四次作业解题参考(P122)2. 常压下,20℃的空气以5m/s 的速度流过一光滑的平面,试判断距离平板前缘0.1m 和0.2m 处的边界层是层流还是湍流。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章1. 对于在r θ平面内的不可压缩流体的流动,r 方向的速度分量为2cos /r u A r θ=-。
试确定速度的θ分量。
解:柱坐标系的连续性方程为11()()()0r z ru u u r r r z θρρρρθθ∂∂∂∂+++='∂∂∂∂对于不可压缩流体在r θ平面的二维流动,ρ=常数,0,0z z u u z∂==∂,故有11()0r u ru r r r θθ∂∂+=∂∂ 即22cos cos ()()r u A A ru rr r r rθθθθ∂∂∂=-=--=-∂∂∂将上式积分,可得22cos sin ()A r A u d f r r θθθθ=-=-+⎰式中,()f r 为积分常数,在已知条件下,任意一个()f r 都能满足连续性方程。
令()0f r =,可得到u θ的最简单的表达式:2sin A u r θθ=-2.对于下述各种运动情况,试采用适当坐标系的一般化连续性方程描述,并结合下述具体条件将一般化连续性方程加以简化,指出简化过程的依据。
(1)在矩形截面管道内,可压缩流体作稳态一维流动; (2)在平板壁面上不可压缩流体作稳态二维流动; (3)在平板壁面上可压缩流体作稳态二维流动;(4)不可压缩流体在圆管中作轴对称的轴向稳态流动; (5)不可压缩流体作球心对称的径向稳态流动。
解: ()0ρρθ∂+∇=∂u(1) 在矩形截面管道内,可压缩流体作稳态一维流动0x z x y z u u u u u u x y z x y z ρρρρρθ∂∂∂∂∂∂∂++++++=∂∂∂∂∂∂∂⎛⎫⎪⎝⎭y 稳态:0ρθ∂=∂,一维流动:0x u =, 0y u = ∴ z 0z u u z z ρρ∂∂+=∂∂, 即 ()0z u zρ∂=∂ (2)在平板壁面上不可压缩流体作稳态二维流动()()()0y x z u u u xyzρρρρθ∂∂∂∂+++=∂∂∂∂稳态:0ρθ∂=∂,二维流动:0z u = ∴()()0y x u u xyρρ∂∂+=∂∂, 又cons t ρ=,从而0yx u u x y∂∂+=∂∂ (3)在平板壁面上可压缩流体作稳态二维流动 在此情况下,(2)中cons t ρ≠∴()()0y x u u xyρρ∂∂+=∂∂(4)不可压缩流体在圆管中作轴对称的轴向稳态流动()()()110r z r u u u r r r zθρρρρθθ∂∂∂∂+++='∂∂∂∂ 稳态:0ρθ∂='∂,轴向流动:0r u =,轴对称:0θ∂=∂ ∴()0z u z ρ∂=∂, 0zu z∂=∂ (不可压缩cons t ρ=) (5)不可压缩流体作球心对称的径向稳态流动22()(sin )()1110sin sin r r u u u r r r r θφρρθρρθθθθφ∂∂∂∂+++='∂∂∂∂ 稳态0ρθ∂='∂,沿球心对称0θ∂=∂,0φ∂=∂,不可压缩ρ=const ∴221()0r r u r r ∂=∂ ,即 2()0r d r u dr= 3.某粘性流体的速度场为22538=x y xyz xz +-u i j k已知流体的动力粘度0.144Pa s μ=⋅,在点(2,4,-6)处的法向应力2100N /m yy τ=-,试求该点处的压力和其它法向应力和剪应力。
解: 由题设 25x u x y =,3y u xyz =,28z u xz =-10316xy xz xz ∇⋅=+-u10x u xy x∂=∂,3y u xz y∂=∂,16zu xz z∂=-∂ 因22()3y y x zyy u u u u p y x y zτμμ∂∂∂∂=-+-++∂∂∂∂ 故 22()3y y x z yy u u u u p y xyzτμμ∂∂∂∂=-+-++∂∂∂∂在点(2,4,-6)处,有22(100)20.144(36)0.14423667N /m 3p =--+⨯⨯--⨯=⨯所以 2()32y x zx xx u u u x y zu p x μτμ∂∂∂++∂∂∂∂=-+∂- 226720.144800.144236366.6N /m =-+⨯⨯-⨯⨯=- 2()32y x zz zz u u u x y zu p z μτμ∂∂∂++∂∂∂∂=-+∂- 234.4N /m =-()yx xy yx u u y xττμ∂∂==+∂∂220.144[527.5N /m 34(6)]=⨯⨯-+⨯⨯-=()yz yzzy u u y zττμ∂∂==+∂∂ 20.144 3.5N /m 324=⨯⨯⨯=()x zzxxz u u z xττμ∂∂==+∂∂ 20.144(41.5N /m 836)=⨯-⨯=-4. 某不可压缩流体在一无限长的正方形截面的水平管道中作稳态层流流动,此正方形截面的边界分别为x a =±和y a =±,有人推荐使用下式描述管道中的速度分布222[1()][1()]4z a px y u z a a μ∂=---∂ 试问上述速度分布是否正确,即能否满足相关的微分方程和边界条件。
解: 在壁面处,即x a =±和y a =±时,0z u =,故满足壁面不滑脱条件;在管道中心,0x y ==时,可得2max4z a p u zu μ∂=-∂=(1)将所给速度分布式代入不可压缩流体连续性方程(2-20),因0x y u u ==可得0zu z∂=∂ 将不可压缩流体的运动方程(2-45c )化简,可得2222()z z u u pz x yμ∂∂∂=+∂∂∂(2)将所给速度分布式分别对x 和y 求偏导数,得2222[1()]()4z a p y xz a au x μ∂=---∂∂∂ 2221[1()]2z p y z a u xμ∂=-∂∂∂ (3)2221[1()]2z p x z a u yμ∂=-∂∂∂ (4)将式(3)和(4)代入式(2)可知,仅当2222x y a +=时才满足运动方程。
因此所给速度分布式不能完全满足运动方程。
5.某一流场的速度向量可以下式表述(,)55x y x y =-u i j 试写出该流场随体加速度向量D D θu 的表达式。
解:y xDu Du D D D D θθθ=+u i j ()()y y y y x x x x x y z x y z u u u u u u u uu u u u u u x y z x y zθθ∂∂∂∂∂∂∂∂=+++++++∂∂∂∂∂∂∂∂i j25[(5)(5)]x -y =+⋅-i j 2525x y =+i j第三章1. 如本题附图所示,两平行的水平平板间有两层互不相溶的不可压缩流体,这两层流体的密度、动力粘度和厚度分别为1ρ、1μ、1h 和为2ρ、2μ、2h ,设两板静止,流体在常压力梯度作用下发生层流运动,试求流体的速度分布。
解:将直角坐标下的连续性方程和运动方程化简,可得221x d u pdy xμ∂=∂ 积分得 21212x p u y C y C xμ∂=++∂因此,两层流体的速度分布可分别表示为 2112112x p u y C y C xμ∂=++∂(1)2212212x p u y D y D xμ∂=++∂(2)由下列边界条件确定积分常数: (1)11;,0x y h u ==(2)22;,0x y h u =-= (3)12;0,x x y u u ==(4)12120,x x du duy dy dyμμ== 将以上4个边界条件代入式(1)与(2),得122111120p C h C xh μ∂++∂=;122222120p D h D xh μ∂++∂=;22C D =;1122C C μμ=解得 2122121112121121h h h p C h x h μμμμμ-∂=∂+1121222121211212221221h h h h p p C h x xh D μμμμμμ-∂∂=-∂∂+-=2212212121122121h h h p D h x h μμμμμ-∂=-∂+2212122212212222221221h h h h p p D h x xh C μμμμμμ-∂∂=-∂∂+-=最后得速度分布方程为212221121212121211121[1(1)]x h h h p h x h y yu h h μμμμμ-∂=-∂+-+-22121221212222222212[1(1)]1x h h h p h x h y y u h h μμμμμ-∂=-∂-+++2. 粘性流体沿垂直圆柱体的外表面以稳态的层流液膜向下流动,如本题附图所示。
试求该流动的速度分布。
该液体的密度和粘度分别为ρ和μ。
解: 由题给条件,有0θ∂='∂,0r u u θ==,z X g =由柱坐标系连续性方程11()()()0r z ru u u r r r z θρρρθ∂∂∂++=∂∂∂简化得0zu z∂=∂由柱坐标系N-S 方程()z z z rz u u u uu u r r zθρθ∂∂∂++∂∂∂ 2222211()z z z u u u p g r z r r rr z ρμθ⎡⎤∂∂∂∂∂=-+++⎢⎥∂∂∂∂∂⎣⎦ 简化得 1()0zg u r r r rρμ+∂∂=∂∂ 由于 0z u z∂=∂,0z u θ∂=∂(轴对称),故()z z u u r =,即 1()0zg du d r r dr drρμ+= 积分得212ln 4z r C g u r C ν+=-+ (1)边界条件为 (1) 0,0z r r u ==(2),0zR du r dr== 将边界条件代入式(1),得 212g C R ρμ=2020(ln )22r g C R r ρμ=- 故速度分布为222001[ln ()]22z g r u R r r r ρμ=+- 3. 半径为r 0的无限长圆柱体以恒定角速度ω在无限流体中绕自身轴作旋转运动。
设流体不可压缩,试从一般柱坐标系的运动方程出发,导出本流动问题的运动方程,并求速度分布与压力分布的表达式。
解:柱坐标系的运动方程为r 方向: 2r r r r r z u u u u u uu u r r r zθθθθ∂∂∂∂++-+'∂∂∂∂ 2222221112()r r r r u u u pX ru r r r r r r z θνρθθ∂∂∂∂∂∂=-++-+∂∂∂∂∂∂⎧⎫⎡⎤⎨⎬⎢⎥⎣⎦⎩⎭ (2-47a )θ方向:r r z u u u u u u uu u r r r zθθθθθθθθ∂∂∂∂++++'∂∂∂∂22222211112()r u u u pX ru r r r rr r z θθθθνρθθθ∂∂∂∂∂∂=-++++∂∂∂∂∂∂⎧⎫⎡⎤⎨⎬⎢⎥⎣⎦⎩⎭(2-47b ) z 方向:z z z z r z u u u u uu u r r zθθθ∂∂∂∂+++'∂∂∂∂ 22222111()z z z z u u u pX r z r r r r z νρθ∂∂∂∂∂=-+++∂∂∂∂∂⎡⎤⎢⎥⎣⎦(2-47c ) 由于该流动具有稳态、对称及一维特性,故有0z θθ∂∂∂==='∂∂∂,0r z u u == 利用上述特点,运动方程(2-47)简化为2u pr rθρ∂=∂22210u u u r r r r θθθ∂∂+-=∂∂ 由于流动为一维,上式可写成常微分方程2u dpdr rθρ= (1)22210d u du u dr r dr r θθθ+-=(2)式(2)的通解为 112u C r C r θ-=+利用边界条件 00,r r u r θω== ,0r u θ=∞=可得21200,C C r ω==因此 20r u rθω=如果令20r Γπω=2则 2u rθΓπ=压力分布为 2228p C rρΓπ=-+由0,r p p =∞= 可得 0C p =因此 222081p p rρΓπ=-4. 试求与速度势2534x xy y ϕ=-++相对应的流函数ψ,并求流场中点(-2,5)的压力梯度(忽略质量力)。
