向量组的线性相关性(2)
《线性代数》教学课件—第4章 向量线性相关 第二节 向量组的线性相关性

9 6
,
有 3 = 21 - 2 , 4 = 1 + 22 , 所以向量组 1,
2 , 3 , 4 线性相关, 其几何意义为: 该向量组所
对应的非齐次线性方程组中的四个方程所表示的
四个平面交于同一条直线. 如图 4.3 .
2x+3y+z=4 3x+8y-2z=13 x-2y+4z=-5 4x-y+9z=-6
x
O M1
图 4.2
M3 a3 RM3 (0,2,2) ,
3y
向量组 a1 , a2 , a3
线性相关,因为
2a1 - a2 - a3 = 0.
(3) 4 维向量组线性相关的几何意义 设有 4 维向量组
2
1
3
4
1T
3
1 4
, 2T
2
45
,
T 3
8
132
, 4T
1
在直线 y =2x 上取三点M1, M2 , M3 , 作三个向量:
6y
5
M3(3,6)
4 3
M2(2,4)
2 1
M1(1,2)
O 123456 x
图 4.1
a1 OM1 (1,2) ,
a2 OM2 (2,4) ,
a3 OM3 (3,6) ,
显然, 这三个向量中的 任意两个向量构成的向 量组都是线性相关的.
证明 向量证组明A 线向性量相组关A, 线等性价相于关齐,次等线价性于齐次线
方程组 方程组 x1a1 + x2a2 x+1a··1·+ x2maa2m+=··0·,+即xmAaxm = 0, 即 Ax = 0
第二节 向量组的线性相关性

定理四 任意n+1个n维向量都是线性相关的.
[证]设n+1个n维向量为: 1=(a11,a12,,a1n) 2=(a21,a22,,a2n)
n=(an1,an2,,ann) n+1=(an+1,1,an+1,2,,an+1,n)
构造向量组: 1=(a11,a12,,a1n,0) 2=(a21,a22,,a2n,0)
故1,2,,n线性无关
例5 讨论向量组1=(1,1,1),2=(0,2,5), 3=(1,3,6)的线性相关性,若线性相关,试写
出其中一向量能由其余向量线性表示的表
达式.
解: 若有k1,k2,k3,使k11+k22+k33=0
即k1(1,1,1)+k2(0,2,5)+k3(1,3,6)=(0,0,0)
k1(1+2)+k2(2+3)+k3(3+1)=0 即(k1+ k3)1+(k1+k2)2+(k2+ k3)3=0 由已知1,2,3线性无关,则
k1 k3 0 1 0 1
k1 k2 0 1 1 0 =2 0
k2 k3 0 0 1 1
齐次方程组只有零解: k1=k2=k3=0
1+2,2+3,3+1线性无关.
若r维向量组1,2,,m线性无关,则r+1维 向量组1,2,,m也线性无关.
[证]反证法
若1,2,,m线性相关
即有不全为零的数k1,k2,,km,使
k11+k22++kmm=0
即 k1(a11,a12,,a1r,a1,r+1)+ k2(a21,a22,,a2r,a2,r+1)+ +km(am1,am2,,amr,am,r+1)=(0,0,,0)
向量组的线性相关性(2)
ar线性
证 用反证法. 若 a1 ,a2 , ar , a r 1线性相关, 则有不全为
k1a1 k2a2
否则 (kr 1 0)
kr 1ar 1 0 其中 kr 不能为零, 1
若 kr 1 0
k1 k2
k1a1 k2a2
ar 1
kr 0
(Ⅰ)
(Ⅱ)
α1α 2
β1β2
αr
βs
若(Ⅰ)中每一个向量都能由向量组(Ⅱ)线性表示,则称 向量组(Ⅰ)可由向量组(Ⅱ)线性表示. 若向量组(Ⅰ) 与向量组(Ⅱ)可以互相线性表示,则称 向量组(Ⅰ)与向量组(Ⅱ)等价. 向量组之间的等价关系具有以下性质:
① 反身性 ② 对称性 ③ 传递性
例 证
设n维向量组α1 , α 2 , , α n 与e1 ,e2 ,
行 向 量
n
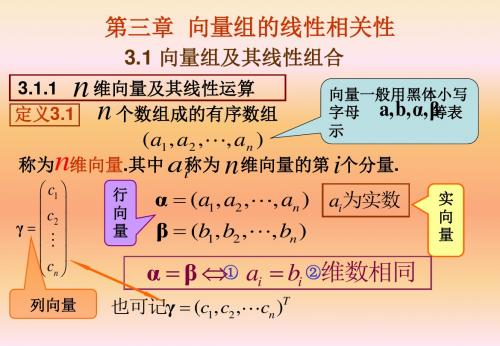
(a1 , a2 ,, an )
α (a1 , a2 , β (b1 , b2 ,
, an ) ai为实数 , bn )
cn )
T
实 向 量
① a b ②维数相同 α β i iFra bibliotek列向量
也可记γ (c1, c2 ,
规定:行向量与列向量都按矩阵的运算规则进行运算. 因 此,n维列向量与 n 维行向量总看成是两个不同的向量
则 (k1 k3 , k1 2k2 3k3 , k1 5k2 6k3 ) 0
1 D1 1 0 2 5 1 3 6
亦即
0
这是关于 k1 , k2 , k3 的齐次方程组
据定 理1.4 有非 零解
即有不全为零的数 k1 , k2 , k3 ,使 从而向量组
k1a1 k2a2 k3a3 0 也可直接求解得 , k1 1, k2 1, k3 1, 即 a1 + a2 - a3 = 0
大学数学基础(2)mooc-向量组的线性相关性(2)

⼤学数学基础(2)mooc-向量组的线性相关性(2)数学基础(2)第三章向量第三讲向量组的线性相关性(2)主讲教师王玮副教授⼆、线性相关的性质定理12(2)1.m m m ααα≥?-向量组,,,线性相关其中⾄少有⼀个向量可由其余个向量线定1性表⽰理12(2)1.m m m ααα≥?-向量组,,,线性⽆关其中任何⼀个向量不可由其余个向推量线性表⽰论121212.m m m ααααααββααα如果向量组,,,线性⽆关,⽽向量组,,,,线性相定关,则可由向量组,,,线性表⽰,且表2⽰式唯⼀理12(2)1.m m m ααα≥?-向量组,,,线性相关其中⾄少有⼀个向量可由其余个向量线定1性表⽰理必要性12121122(2)0m m m m m k k k k k k αααααα≥+++=若向量组,,,线性相关,则存在不全为零的数,,,,使得10k ≠不妨设,11.m α-即可由其余个向量线性表⽰32123111m mk k k k k k αααα=-+-+- ? ? ?则有找等式,看系数12(2)1.m m m ααα≥?-向量组,,,线性相关其中⾄少有⼀个向量可由其余个向量线定1性表⽰理充分性1m -设向量组中⾄少有⼀个向量可由其余个向量线性表⽰,1211122111(1)0m m m m k k k k k k αααα----++++-=因此存在⼀组不全为零的数,,,,,使得12m ααα故向量组,,,线性相关.1211122111m m m m m m k k k k k k ααααα----=+++不妨设可以由其余个向量线性表⽰,即存在⼀组数,,,,使得12(2)1.m m m ααα≥?-向量组,,,线性⽆关其中任何⼀个向量不可由其余个向推量线性表⽰论121212.m m m ααααααββααα如果向量组,,,线性⽆关,⽽向量组,,,,线性相定关,则可由向量组,,,线性表⽰,且表2⽰式唯⼀理121211220m m m m k k k k k k k k αααβαααβ++++=证由,,,,线性相关知:存在不全为零的数,,,,,使得①k ≠1211220m m m k k k k k k ααα+++=否则,①变为存在不全为零的数,,,,使得12m ααα这与向量组,,,线性⽆关⽭盾. 12120m mk k k k kkkβααα≠=----,12m βααα即可由向量组,,,线性表⽰.找等式,看系数下⾯证明表⽰法唯⼀121212.m m m ααααααββααα如果向量组,,,线性⽆关,⽽向量组,,,,线性相定关,则可由向量组,,,线性表⽰,且表2⽰式唯⼀理1122m m l l l βααα=+++假设,111222()()()0m m m l l l µαµαµα-+-++-=两式相减得121122m m ml l l αααµµµ===由向量组,,,线性⽆关知,,,得证1122m m βµαµαµα=+++,121211*********.,,,(3)(A ),,,0(B ),,,(C ),,,(D ),,,s s s ss s s n s n k k k k k k ααααααααααααααα≤≤+++≠维向量组线性⽆关的充要条件是存在⼀组不全为零的数,使中任意两个向量都线性⽆关中存在⼀个向量,它不能由其余向量线性表⽰中任意⼀个向量都不能⽤其余向量线性表⽰【典型例题】D(A )(B )(C ).、、是此向量组线性⽆关的必要条件,但不充分条件12112212,,,0,,,.(D ).s s ss k k k k k k αααααα+++=解向量组线性⽆关的定义是关系式,只能在全为零时才成⽴对照这⼀定义知,只有正确√1231232.(1,0,0),(1,1,0),(1,1,1),(,,).,,.a b c αααββααα====判断下列命题是否正确:设向量组则⼀定可由线性表⽰,且表达式唯⼀121212,,,,,,,,,,,,.m m m ααααααββααα向量组线性⽆关,⽽向量组线性相关则可由线性表⽰且表⽰法唯⼀数学基础(2)第三章向量第三讲向量组的线性相关性(2)END。
32向量组的线性相关与线性无关(二)详解

解: (4) 由定理3.2.3知,5个四维向量必定线性相关.
13
例.证明:若 , , 线性无关, 则 , , 也线性无关
证:设 k1( ) k2( ) k3( ) O (*) (目标: ki = 0)
则
(k1 k3 ) (k1 k2 ) (k2 k3 ) O
7
3.2.3向量组的线性相关性的判定
1.向量组线性相关的条件: 设向量组
α1
a11 a21
an1
,
α2
a12 a22
an2
,
, αm
a1m a2m
anm
,
它线性相关还是线性无关,取决于齐次线性方程组
k1α1 k2α2 kmαm 0
a11x1 a12x2 a1m xm 0
(3-14)
只有零解. 考虑 β1, β2, β3相对应的齐次线性方程组
a11x1 a21x2 a31x3 0
aa1123
x1 x1
a22 x2 a23x2
a32 x3 a33 x3
0 0
(3-15)
aa1154
x1 x1
a24 x2 a25 x2
a34 x3 a35 x3
0 0
方程组(3-14)的每一个解都是方程组(3-15)的解.而方程组(3-14)
(3) α1 1, a, a2, a3 T , α2 (1,b,b2,b3)T , α3 (1, c, c2, c3)T ,
α4 (1, d, d 2, d 3)T,其中a,b,c,d各不相同. (4) α1 ( 2, 3, 4, 1)T , α2 ( 2, 1, 4, 0)T , α3 ( 1, 3, 0, 1)T ,
即: a1, a2 ,, am 线性无关
2 向量组的线性相关性

则向量b是向量组A的线性组合,这时称向量 b 能 由向量组 A 线性表示.
注意
也可用矩阵形式表示: 1若所给向量均为行向量, 则有
2若所给向量均为列向量, 则有
返回
上一页 下一页
二、线性相关性的概念
定义3 给定向量组A :1,2 , ,m ,如果存在不
全为零的数k1, k2 , , km使
所以
线性无关。
返回
上一页 下一页
定理1 向量组
(s≥2)线性相关的充要条件
是其中至少有一个向量能由其他向量线性表出。
证 充分性:设
中有一个向量能由其他向
量线性表出,不妨设
所以
线性相关。
必要性:如果
线性相关,就有不全为零的
数k1,k2,…,ks,使 设k1≠0,那么
即 能由
线性表出。
返回
上一页 下一页
k11 k2 2 km m 0
则称向量组A是线性相关的,否则称它线性无关.
注意
1. 若 1 , 2 , , n线性无关,则只有当
1 n 0时,才有
11 2 2 n n 0成立 .
2. 对于任一向量组,不是线性无关就是
线性相关 .
3.向量组只包含一个向量 时,若 0则说 线性相关,若 0,则说 线性无关 .
如果
有
向量组
中每一个向量都可以经向量组
线性表出。因而,向量组
可以经向量组
线性表出。
返回
上一页 下一页
向量组的等价具有下述性质:
(1)反身性:向量组
(2)对称性:如果向量组
那么
也与
与它自己等价;
与 等价。
等价,
第二节 向量组的线性相关性

a1,a2线性相关 向量a1,a2共线(平行) a1 ka2
3) A含三个向量时:
a1,a2,a3线性相关 向量a1,a2,a3共面.
2.等价定义
向量组 1 , 2 ,,(当 m 2 时)线性相关 m 的充分必要条件是 1 , 2 , , m 中至少有一个向 量可由其余 m 1个向量线性表示. 证明 充分性 设 a1 , a2 , , am 中有一个向量(比如 能由其余向量线性表示. 即有
由R( A) R( B ) m , 知方程组 ( 1 , 2 ,, m ) x b有唯一解,即向量 能由向量 b 组A线性表示,且表示式唯 . 一
例 设 向 量 组 1 , a 2 , a 3线 性 相 关 , 向 量 组 , a 3 , a 4 a a2 线性无关,证明 : (1) a1能 由a 2 , a 3线 性 表 示 ; ( 2 ) a 4不 能 由 1 , a 2 , a 3 线 性 表 示 a .
am)
am 1 1 2 2 m1 m1
故
1 1 2 2 m1 m1 1am 0
因 1 , 2 , , m 1 , 1 这 m 个数不全为0,
故 1 , 2 , , m 线性相关. 必要性 设 1 , 2 , , m 线性相关, 则有不全为0的数 k1 , k 2 ,, k m , 使
第二节
向量组的线性相关性
一、线性相关、线性无关
1.定义4 给定向量组 A : 1 , 2 ,, m , 如果存在不
全为零的数 k1 , k 2 ,, k m 使 k1 1 k 2 2 k m m 0
则称向量组A是么意思?
第二章 第二讲 向量组的线性相关性(2013-3-21)

k1α1 + k2α 2 + ⋯ k sα s = 0
(1)
1 2 s
... ... (2.1)
若, k , k ⋯ k 不全为零(2.1)式成立,则称向量组 α ,α ,⋯α 线性相关; (2) 若当且仅当 k , k ⋯ k 全为零, (2.1)式成立,称向量组 α ,α ,⋯α 线性无关 . 定义 2.2.1 易验证以下结论的正确性: (1)任意一个包含零向量的向量组必线性相关. (2)两个非零向量线性相关的充分必要条件是它们的对应分量成比例. 定理 2.2.1 (1) 如果向量组 α ,α ,⋯,α 中有一部分组线性相关,则向量组 α , α ,⋯, α 必线性相关. (2)如果向量组 α ,α ,⋯,α 线性无关,则任何部分组必线性无关. 证明( 证明(1) 假设该组向量中 α ,α 线性相关,由定义 2.2.1 必存在 k , k 不全为零,使 得 k α +k α =0 成立。取一组不全为零的数 k , k ,0,0,⋯,0 ,有 k α +k α +0α + ⋯ +0α =0 成立,故 α , α ,⋯, α 线性相关。 证明(2)用反证法即可证得。 定理 2.2.2 如果向量组 α ,α ,⋯,α 线性无关,而向量组 α ,α ,⋯,α , β 线性相关, 则 β 可由向量组 α ,α ,⋯,α 线性表出且表达式唯一.
3 3
解 令 x α +x α +x α
=0
,得齐次线性方程组
其系数矩阵的最简形
−2 x1 + x2 + x3 = 0 x1 − 2 x2 + x3 = 0 x + x − 2x = 0 1 2 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
向量组线性无关;
(2)当D 0即c 0或c -3时,方程组有非零解,
向202量1/2/组5 线性相关。
8
例 判别向量组1 (1,1,1),2 (0,2,5),3 (1,3,6)
的线性相关性。
解法1 设数k1,k2,k3,使 k11 k22 k33 0
即 (k1 k3,k1 2k2 3k3,k1 5k2 6k3 ) 0
,,m
,
)
0
0
1
bm
0
0
0
0
0
0
0
0
故 2021/2/5
b11
b22
bm m
21
所以
xi bi
例 已知 1 (1,1,1),2 (1,0,1), (1, 3, 5) 将用1,2线性表示,且表示式唯一。
解 1. 1,2 不成比例,线性无关;
2. 设 x11 x22 即
设 a1 , a2 ,, am 中有一个向量(比如am )
能由其余向量线性表示. 即有
am 11 2 2 m1 m1
2021/2/5
15
故 11 22 m1 m1 1am 0 因 1 , 2 ,, m1 , 1 这m m 个数不全为0,
故 1 ,2 ,,m 线性相关. 必要性 设 1 ,2 ,,m 线性相关,
an x 1,1 1 an1,2 x2 an1,m xm 0,
由于向量组A线性无关,则一下方程组只有零解
a11x1 a12 x2 a1m xm 0,
a21x1 a22 x2 a2m xm0,
an1x1 an2 x2 anm xm 0,
由于的解一定是的解,所以只有零解,
所以
k1 k2 kn 0
因而 1,2,,n 线性无关。
2021/2/5
11
P82
例2
已知向量组1
,
2
,
线性无关,试证明:
3
(1)1 1 2 , 2 2 3, 3 3 1线性无关;
(2)1 1 -2 , 2 2 -3, 3 3 -1线性相关。
证 设有x1, x2, x3使
第四节 向量组的线性相关性
2021/2/5
1
一、向量组的线性相关和线性无关
定义6 给定向量组A :1,2,,m,如果存在不
全为零的数k1, k2,, km使
k11 k22 kmm 0
则称向量组A是线性相关的,否则称它线性无关.
注 1. 若 1,2, ,n 线性无关 ,则只有k1 kn 0 时,才有 k11 k22 knn 0 成立 .
定理7 设 1,2,,m 线性无关,而1,,m, 线性 相关,则 能由1,,m 线性表示,且表示式是唯一的.
证明 由于1,2,,m, 线性相关,故有不全为0的数
k1,, km , km1, 使 k1a1 kmam km1 0 成立
若 km1 0, 则 k1a1 kmam 0
由于 1,2,,m 线性无关,所以 k1 k2 km 0
k1a1 k2a2 0a3 0as 0
2021/所2/5以 a1,, as 线性相关.
25
(2) 设 x11 x22 xmm 0
a11x1 a12 x2 a1m xm 0,
即
a21x1 a22 x2 a2m xm 0,
an1x1 an2 x2 anm xm 0,
3
由定义,向量组
a1 j
A: j
a2
j
(
j
1,2,, m)
anj
线性相关等价于齐次线性方程组 x11 x22 xmm 0
a11x1 a12 x2 a1m xm 0, 即 a21x1 a22 x2 a2m xm0, 有非零解。
an1x1 an2 x2 anm xm 0,
则有不全为0的数 k1 , k2 ,, km , 使
k11 k22 kmm 0.
2021/2/5
16
因k1 , k2 ,, km 中至少有一个不为0,
不妨设 k1 0,则有
1
k2 k1
2
k3 k1
3
km k1
m .
即 1 能由其余向量线性表示.
证毕.
2021/2/5
17
向量组A线性无关等价于此方程组只有零解。
2021/2/5
4
定理5
向量组
a1 j
A: j
a2
j
(
j
1,2,, m)
anj
线性无关当且仅当R(A)=m;
线性相关当且仅当R(A)<m.
推论 m个n维向量组成的向量组,当维 数n<m时一定线性相关。
特别,n+1个n维向量一定线性相关。
2021/2/5
(1, 3, 5) x1(1,1,1) x2 (1,0,1)
(x1 x2,x1,x1 x2 )
所以
x1
x1
x2
1 3
由A~
1 1
1 0
1 3
1 0
0 1
3 2
x1 x2 5
故 = -31+22 ,
2021/2/5
22
即1,2线性无关, 1,2,线性相关 故:可以用1,2线性表示,且表示式唯一。
2021/2/5
23
定理8 (1)若向量组的一个部分组线性相关,则 整个向量组线性相关。
逆否命题 若一个向量组线性无关,则其任何一个
部分组线性无关。
a1 j
(2)如果向量组
A: j
a2
j
(
j
1,2,, m)
线性无关,
anj
在其每个向量上添加一个分量所得的n+1维向量组B:
2021/2/5
x11 x22 x33 0
即 x(1 1 2) x2 ( 2 3 ) x3 ( 3 1 ) 0,
亦即( x1 x3 )1 ( x1 x2 ) 2 ( x2 x3 ) 3 0, 因1, 2, 3线性无关,故有
x1 x3 0, x1 x2 0,
2021/2/5
c )k1 (1
k c)k
2 2
k3 k3
0 0
只有零解
k1 k2 (1 c)k3 0
1c 1 D 1 1c
1 r2 r1 1 c 1 1 r3 (1c)r1
1 c c 0 c2(3 c)
1 1 1c
c2 c 0
由克莱姆法则
(1)当D 0即c 0且c -3时,方程组只有零解,
24
a1 j
a2 j
j
( j 1,2,, m)
anj
an 1,
j
也线性无关。
逆否命题 若向量组B线性相关,则向量组A线性相关。
证明 (1) 不妨设 a1, , as 中a1, a2线性相关,
则存在不全为 0 的数 k1, k2 , 使得 k1a1 k2a2 0
即存在不全为0的数 k1, k2,0,,0使得
2. 只有一个向量 的向量组,若 0则说 线性相关,
若 0,则说 线性无关 .
2021/2/5
2
3.任何包含零向量的向量组是线性相关的。
4.对于含有两个向量的向量组,它们线性相 关的充要条件是两向量的分量对应成比例,几 何意义是两向量共线;三个向量线性相关的几 何意义是三向量共面。
2021/2/5
则 向量组A线性相关。
推论2 等价的线性无关向量组所含向量个数 相等.
证明 设向量组A与B等价,A组的向量个数为r,
B的向量个数为s,由推论1,有 r≤ s,且s ≤ r,所
以 r =s。
2021/2/5
28
么么么么方面
• Sds绝对是假的
例3 P84 设向量组 1,2 ,3 线性相关,向量组
2,3,4 线性无关,证明:
此时与 k1,, km , km1 不全为0矛盾,
因而 km1 0,
2021/2/5
1 k m1
(k1a1
kmam 18
)
因此 可由 a1,, am 线性表示.
再证表示式的唯一性 设有两个表示式
1a1 mam 和 1a1 mam
两式相减,得
(1 1)a1 (m m )am 0
推论1 如果向量组A:a1, a2 ,, as 可由向量组 B:1,2 ,, t ,线性表示,且向量组A线性无
关,则s≤ t。
2021/2/5
27
例如:向量组A:1 (1,1),2 (0,2),3 (1,3)
向量组B:1 (1,0),2 (0,1)
显然,向量组A可由向量组B线性表示; 向量组A的个数 r=3,向量组B的个数 s=2, 故 r>s
D 1 2 3 1 1 56 15
15 6
故此方程组有非零解
3 3 0
1, 2 , 3 线性相关
2021/2/5
10
例 证明向量组 1 (1,0,,0),2 (0,1,,0),, n (0,0,,1) 线性无关。
证设
k11 k2 2 kn n 0
即 (k1,k2,,kn)(0,0,,0)
x2 x3 0.
12
由此方程组的系数行列式
101 D 1 1 0 20
011
所以方程组只有零解,即x1=x2=x3=0。从而向量
组1,2,3线性无关。
2021/2/5
13
(2) 设有k1,k2,k3使得 k11 k2 2 k3 3 0
即 k1(1 -2 ) k2(2 -3 ) k3(3 -1) 0
因 a1,, am线性无关,所以 i i 0 即
i i (i 1,2,, m).
202即1/2表/5 示式唯一.
19
