连续介质力学-例题与习题
张量分析——精选推荐

《连续介质力学》例题和习题第一张、矢量和张量分析第一节 矢量与张量代数一、 矢量代数令 11223A A A =++A e e e 112233B B B =++B e e e 则有 11223A A A αααα=++A e e e 11122233()()()A B A B A B +=+++++A B e ee 1122331122331122()()A A A B B B A B A B A B ∙=++∙++=++A B e e e e e e112233112233111112121313212122222323313132323333()() A A A B B B A B A B A B A B A B A B A B A B A B ⨯=++⨯++=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯A B e e e e e e e e e e e e e e e e e e e e e e e e 又因为 11⨯=e e 0 123⨯=e e e 132⨯=-e e e 213⨯=-e e e 22⨯=e e 0 231⨯=e e e 312⨯=e e e 321⨯=-e e e 33⨯=e e 0则 2332131132122(_)()()A B A B A B A B A B A B⨯=+-+-A B e e e习题1、证明下列恒等式:1)[]2()()()()⨯∙⨯⨯⨯=∙⨯A B B C C A A B C2) [][]()()()()⨯∙⨯=∙⨯-∙⨯A B C D A C D B B C D A2、请判断下列矢量是否线性无关?1232=-+A e e e 23=--B e e 12=-+C e e .其中i e 单位为正交的基矢量。
*补充知识:矩阵及矩阵运算1、定义:[]()111213212223313233,1,2,3ij A A A A A A A i j A AA ⎡⎤⎢⎥⎡⎤===⎣⎦⎢⎥⎢⎥⎣⎦A i 表示行,j 表示列;m 和n 相等表示为方阵,称为m (或n )阶矩阵。
连续介质力学-第3章-四川大学
n
t (n)
n
t(n) (n) 1
t(n) 2
0
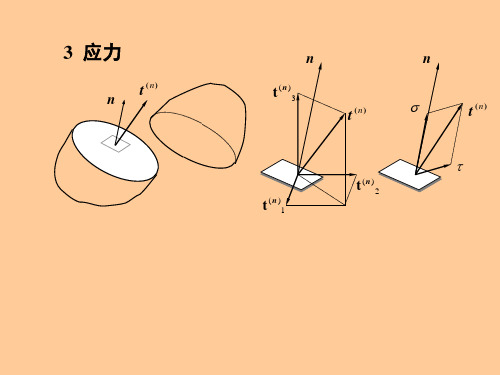
一点的应力状态包括经过这点的所 有方向上的应力矢量
Cauchy定理:
如果空间某点x处的张量 是通过x的微元面 da的法线n的连续函数,则存在比 高一阶的
张量s(x : t),使
成立。
(x, n; t) s(x; t) n
几个和应力有关的概念:
➢ 三个主应力
➢ 应力的主平面 主应力曲面(3D),主应力迹线(2D)
➢ 平均正应力,应力偏量
T
1 3
IT I
T
➢ 最大切应力
max
1 2
( 1
3)
1 2
(
1
3)
方向: 与第一主轴和第三主轴成45°的夹角
➢ 八面体应力
oct
n t (n)
如果要求K点处法线方向为 n 的斜截面上的法向应力 ,
只需在该点处的应力张量 T 的前后分别点乘单位矢量 n
即可,即
T11 T12 T13 n1
n T n nT Tn n1
n2
n3 T21
T22
T23
n2
T31 T32 T33 n3
Cauchy应力张量
T11 T12 T13 e1
T (e1
e2
e3 )T21
T22
T23
e
2
Tij ei e
j
T31 T32 T33 e3
对于应力状态,人们常采用单元体的表示方法, 即:将这一点“放大”为一个微元六面体,并取其六 个面分别平行于坐标面,这样的微元六面体就称为单 元体。单元体的六个面上的应力表示过该点的法线方 向与坐标轴正向重合或相反的六个微元面上的应力。 根据作用力与反作用力相等的原理,单元体中相对表 面的应力矢量总是大小相等而方向相反的。
连续介质力学第三次作业习题和解答

[
]
[
]
在流入面: v1 = −v1 * n1 ,在流出面: v2 = v2 * n1
2、给定速度场 v1 = ax1 + bx2 , v2 = ax2 + bx1 , v3 =
x1 + x2 , ρ 0 = ρ * e −2 at 。其中 a,
2 2
b,c,ρ为常数 求:是否满足质量守恒方程 解答: 质量守恒方程:
∫ [t − ρ * v(v • n )]dS
S1
C
=
S1 + S 2 + S 3 + S 4
∫ [t − ρ * v(v • n)]dS ∫ [− p n
2 S3
C
= =
∫ [t − ρ * v(v • n )]dS + ∫ [t − ρ * v(v • n )]dS + ∫ [t − ρ * v(v • n )]dS + ∫ [t − ρ * v(v • n )]dS
(
)
3、
Ω • r = w× r
w × r = eijk w j rk ei
•
Ω • r = Ωim rm ei
所以
• •
•
•
eijk w j rk = Ωim rm
eijk w j = Ωik
⎡ 0 Ω=⎢ ⎢ w3 ⎢ ⎣− w2
•
− w3 0 w1
w2 ⎤ − w1 ⎥ ⎥ 0 ⎥ ⎦
4、
L = ∫ ρ * r × vdv = ∫ ρ * r × (w × r )dv = ∫ ρ [w(r • r ) − r (r • w)]dv = ∫ ρ [(r • r ) − (r ⊗ r )]dv • w
连续介质力学1-5
x i i i x i
Ti j i i jjTij
Ti j i i jjTij
1 1 21 31
?T
21 22 23
0
ij
12 22 32
不为零 的只有
i j k l; i k j l;
i jkl il jk
(2)绕x3旋转900
0 1 0 ij 1 0 0 0 0 1
x1 x2 , x2 x1 , x3 x3
Aijkl Aijkl ii jj kk l l Aijkl
A11→A22
A22→A33
A33→A11 A11=A22=A33
A12→A23
A23→A31
A31→A12
A12=A23=A31
A21→A32
A32→A13
A13→A21
A21=A32=A13
(2)作旋转变换
x1 x1 , x2 x2 , x3 x3
1 0 0 ij 0 1 0 0 0 1
例如:(2,3,1)为(1,2,3)的一个偶排列,{1→2,2→3,3→1}可 视为一次完成的,称之为置换。
推论:在任意置换下,张量的每一分量被换成另一分量, 如该张量为各向同性张量,则这两个分量相等。
(1)先说明置换是旋转变换的特例
T11 T12 T13 T21 T22 T23 T T32 T33 31
Aijkl=λδijδkl+μ(δikδjl+δilδjk)
习题
ˆ 3e e e e e e 3e e e e 1. T 1 1 1 2 2 1 2 2 3 3 (1)求主值和主方向; ˆ ( 2)写出T在主方向坐标架下的表达式; ˆ ( 3)写出T从e i 标架变换到主方向坐标架的变换形式; ˆ ( 4)计算T 2的主值和主方向(用原标架,检验定理)。
连续介质力学 习题 1

Continuum MechanicsHomework #1Due: Tuesday March 23, 2010In completing the following problems, you may use Maple, Mathematica or Matlab to carry out some of the detailed calculations. If you do so, please attach a printout of the script showing your commands and results from the software.1. For the tensor and vector quantities given below, please (a) carry out the specific operations using the indicial notation, and (b) give the components of the resulting quantity for each operation.[][]{}{}11101212122,231,2,201233202⎡⎤⎡⎤⎧⎫⎧⎫⎪⎪⎪⎪−−−⎪⎪⎪⎪⎢⎥⎢⎥⎪⎪⎪⎪⎢⎥⎢⎥⎪⎪⎪⎪⎪⎪====⎢⎥⎢⎥⎨⎬⎨⎬⎪⎪⎪⎪⎢⎥⎢⎥⎪⎪⎪⎪⎢⎥⎢⎥⎪⎪⎪⎪−⎪⎪⎪⎪⎢⎥⎢⎥⎪⎪⎪⎪⎩⎭⎣⎦⎣⎦⎩⎭A B u v(i) :A B and ⋅⋅A B(ii) ×u v and ×v u (iii) ⋅B u and ⋅u B (iv) ⊗u v and ⊗v u2. Suppose A and B are second order tensors and u , v , and w are vectors. Use the index notation to show that the following relations hold.(i) ()T T T =AB B A(ii) ()111−−−=AB B A(ii) ()().×⋅=⋅×u v w u v w(iii) ()()().××=⋅−⋅u v w u w v v w u3. Indicate whether or not the following tensor equations are mathematically proper. If an equation is inadmissible, please provide a reason as to why. Note that A , B , and D are second-order and v is first-order.(i) ⋅+=A B A D (ii) ⋅⋅=A B v (iii) (),,,,12ij i j j i k i k j E u u u u =++ (iv) ,0ij ji A u +=(v) ,,ij i kk j mno oj mn A B K D ε+=(vi) ij im jn mnkl kl kk ll mn A C D B ααηη+= (vii) (),,ij j ijkl kl j C E Σ=4. If A and B are second order tensors, calculate ()−tr AB BA .5. Consider the 3-dimensional Cartesian space with basis vectors ()1,2,3i i =e aligned with respect to the 1x , 2x , and 3x axes. Find the rotation matrix []Α for the following changes of coordinates:(i). a rotation of 90 degrees about the 3x axis. (ii). a rotation of 180 degrees about the 2x axis.(iii). a rotation of -45 degrees about the 2x axis, followed by a rotation of 45 degreesabout the 3x axis.(iv). a rotation of 180 degrees about the 3x axis, followed by a 90 degrees about 1xaxis, followed by a -90 degrees about the 2x axis.6. Tensor A has the representation of []211111111⎡⎤⎢⎥⎢⎥=−⎢⎥⎢⎥⎢⎥−−⎢⎥⎣⎦A in some basis.(i). Calculate the invariants of A .(ii). Write the characteristic equation of A .(iii). Find all eigenvalues and eigenvectors (the eigenvectors should be normalized). (iv). Show that the eigenvectors of A are mutually orthogonal.(v). Does A have eigenvectors that are other that the three you found? Why or whynot?7. Problem 2.4 on page 42 of Mase, Smelser & Mase (textbook).8. Problem 2.6 on page 43 of Mase, Smelser & Mase (textbook).。
2012年连续介质力学试题

2011—2012学年第 4学期连续介质力学课程期末考试试卷(A卷)e e⋅=,i j2011—2012学年第 4学期连续介质力学课程期末考试试卷(A卷)O Ox x y y2011—2012学年第 4学期连续介质力学课程期末考试试卷(A卷)2011—2012学年第 4学期连续介质力学课程期末考试试卷(A卷)答案及评分标准2011—2012学年第 4学期连续介质力学课程期末考试试卷(A卷)答案及评分标准2、axy y x 622=∂∂=φσ22212ax xy =∂∂=φσ 223ay yx xy-=∂∂∂-=φτ(3分)3ah 23ah 23al 23alh3ah 2xy(4分)五、证明题(本大题25分)1、证明:假想从物体内任意点P 取出一个微分四面体元PABC ,如图。
斜截面ABC 离开O 点一微小距离 h ,它的外法线为 n 。
(2分)设已知作用于截面 PBC ,PAC ,PAB 上的合应力矢量分别为T 1,T 2,T 3,于是,作用于与坐标轴X i 垂直的面元上的合应力矢量i T 可由沿坐标轴方向的分量表示为j ij ie T σ=。
(3分)设面元 ABC 的面积为 dA ,则其余与轴 x j 垂直的各截面的面积为()dA n n x dA dA j j j ==,cos ,这里的n j 是斜截面ABC 的外法线n 的方向余弦。
(2分)根据应力连续性的假设,应力矢量在物体内是连续变化的,作用在截面ABC 上的应力分量的合力为dA T i n;同理作用在PBC ,PCA 与PAB 等截面上的应力分量的合力为dA n j ij σ-,前取负号是因为dA j 的外法线与X j 轴的正方向相反;体力F 的分量为F i hdA/3,其中hdA/3是四面体的体积。
(3分)至此,可以列出四面体的平衡方程:2011—2012学年第 4学期连续介质力学课程期末考试试卷(A卷)答案及评分标准。
连续介质力学习题二答案
连续介质力学习题二答案连续介质力学是力学中的一个重要分支,研究的是连续介质的宏观性质和行为。
在学习连续介质力学的过程中,习题是不可或缺的一部分。
下面将为大家提供一些连续介质力学习题的答案,希望能对大家的学习有所帮助。
1. 一个均匀的弹性杆,长度为L,横截面积为A,杨氏模量为E。
如果在杆的一端施加一个拉力F,另一端固定,求杆的伸长量。
解答:根据胡克定律,弹性杆的伸长量与施加的拉力成正比。
所以,伸长量可以用下面的公式表示:ΔL = (F * L) / (A * E)其中,ΔL表示伸长量,F表示施加的拉力,L表示杆的长度,A表示横截面积,E表示杨氏模量。
2. 一个圆柱形的液体容器,底面半径为R,高度为H。
如果在容器的底部施加一个压力P,求液体容器内部的压强分布。
解答:液体容器内部的压强分布可以用下面的公式表示:P(z) = P + ρ * g * z其中,P(z)表示液体容器内部距离底部高度为z处的压强,P表示底部施加的压力,ρ表示液体的密度,g表示重力加速度。
3. 一个均匀的弹性球体,半径为R,杨氏模量为E。
如果在球体的表面施加一个压力P,求球体的压缩量。
解答:根据胡克定律,弹性球体的压缩量与施加的压力成正比。
所以,压缩量可以用下面的公式表示:ΔR = (P * R^3) / (3 * E)其中,ΔR表示压缩量,P表示施加的压力,R表示球体的半径,E表示杨氏模量。
4. 一个均匀的弹性体,体积为V,体积弹性模量为K。
如果在弹性体的体积上施加一个压力P,求弹性体的体积变化量。
解答:弹性体的体积变化量可以用下面的公式表示:ΔV = -(P * V) / K其中,ΔV表示体积变化量,P表示施加的压力,V表示弹性体的体积,K表示体积弹性模量。
以上是一些连续介质力学习题的答案,希望对大家的学习有所帮助。
在学习连续介质力学的过程中,多做习题是非常重要的,通过解答习题可以加深对理论知识的理解和运用。
同时,也希望大家能够在学习中保持耐心和积极性,相信通过不断的努力,一定能够掌握连续介质力学的知识。
连续介质力学-
连续介质力学1、连续介质力学作业〔第二章〕习题连续介质力学作业〔第二章〕习题1、初始构型和当前构型的转换关系:211X22Xx+=,212XX22x+=,33Xx=其中()321,,XXX为一个物质点在初始构型上的坐标,()321,,xxx为同一个物质点在当前构型上的坐标。
参考基是~3~2~1,,eee标准正交基求:〔1〕变形梯度F〔2〕右Cauchy-Green变形张量C〔3〕Green变形张量E〔4〕初始构型上一向量~33~22~11~eXeXeXX++=,变形后在当前构型上是~x,证明~~~~XCXxx??=?和()~~~~~~2XEXXXxx??=〔5〕左Cauchy-Green变形张量b〔6〕Almans2、i变形张量A2、一个连续体内的任意一点,初始时刻坐标为()YX,,经过t时刻后,变为()yx,,其中:atYXx+=,Yy=,其中a是常数。
求:〔1〕变形梯度F〔2〕Green变形张量E〔3〕速度梯度L〔4〕变形张量率?ε〔5〕Green应变速率?E3、证明:〔1〕若B为客观张量,证明2B,nB是客观张量。
〔2〕若M、N为客观张量,证明NM?是客观张量。
4、横截面为圆形的杆,单轴拉伸,拉力为~P,初始长度L,半径R;当前长度l,半径r。
如图:初始时刻坐标为()ZYX,,,经过t时刻后,变为()zyx,,。
Xx1λ=Yy2λ=Zz3λ=其中Ll=1λRr==32λλ求:〔1〕R,F,U,V〔2〕C,E,b,3、A〔3〕验证:当1λ,2λ,3λ趋近于1的时候,E和A近似相等〔4〕L 〔5〕?E,?ε〔6〕Cauchy应力σ,2ndP-K应力S,1stP-K应力P〔7〕验证dVFPdVESdvVVv∫∫∫==:::εσ~Plr~PLRxzy5、匀称拉杆受轴向拉力,拉力同时也随杆一起转动。
考虑二维状况,取笛卡尔坐标系,初始水平状态,x方向轴向应力k,逆时针旋转,转速为ω,经过t时刻后。
求:〔1〕还是参考笛卡尔坐标系,求Cauchy应力σ〔2〕?σ〔3〕速度梯度L〔4〕?ε〔5〕Cauchy应力的Jaumann速率JC?σ可验证:?ε为0时,?σ不为0,不能直接建立二者之间的本构关系。
连续介质力学作业(第一章)答案
连续介质力学作业(第一章)习题1. 向量~~~~k z j y i x a ++=。
~i ,~j ,~k 表示三维空间中标准正交基。
给定一组协变基~~12i g =,~~~2j i g +=,~~~3k j g +=。
(1)求逆变基1g ,2g ,3g 。
(2)求ij g(3)向量~a 参考逆变基~1g ,~2g ,~3g 表示时,~~i i g a a =,求i a 。
(1)[]222~~~~~~~~~3~2~1= +•= +• +×=• ×=k j k k j j i i g g g g+−=+× += ×=~~~~~~~~3~2~121211i j k k j j i g g g g~~~~~~1~3~22211j k i k j g g g g +−= × += ×=~~~~~2~1~32211k j i i g g gg =+×= ×=(2) g ij =gg ii ⋅gg jj �g ij �=�3/4−11/2−12−11/2−11�(3)a i =aa ⋅gg ii a 1=2x,a 2=x +y,a 3=y +z2. 已知笛卡尔坐标系331e e e ,,,一个新的坐标系定义为−−−= ′′′32132161312161312162310e e e e e e 向量321e e e x 321x x x ++=,给定函数2321x x )f(−=x 。
(1) 求函数f 的梯度)(f grad(2) 求向量x 参考新坐标系的表示形式i ′′=e x i x(3) 求函数f 在新的坐标系下的表达形式),,(321′′′′x x x f (4) 判断)(f grad 的客观性。
3. 二维情况下,一质点应力张量σ主值6.11=σλ,3.22=σλ。
主方向2112123e e N −=,2122321e e N +=。
连续介质力学1-5
不为零 的只有
i = j = k = l; i = k ≠ j = l;
i= j≠k=l i=l≠ j=k
(2)绕x3旋转 0 绕 旋转90
0 1 0 {β i′j } = − 1 0 0 0 0 1
x1′ = x 2 , x 2′ = − x1 , x 3′ = x 3
推论:在任意置换下,张量的每一分量被换成另一分量, 推论 在任意置换下,张量的每一分量被换成另一分量, 在任意置换下 如该张量为各向同性张量,则这两个分量相等。 如该张量为各向同性张量,则这两个分量相等。 (1)先说明置换是旋转变换的特例 先说明置换是旋转变换的特例
T11 T12 T13 T21 T22 T23 T T32 T33 31
第五章 各向同性张量
r = xi ′ ei ′ = xi ei xi ′ = β i ′i xi
x1′ cos θ = x 2′ − sin θ
问:是否可能 是否可能
x2′ x 2
θ
r
x1′
x1
sin θ x1 x cos θ 2 sin θ x1 x1 x = x cos θ 2 2
− 1 0 0 {β i′j } = 0 − 1 0 0 0 1
Aijkl = Ai′j′k′l ′ = β i′i β j′j β k′k β l ′l Aijkl
i ′、j ′、k ′、l ′中有单数个 3时, Ai ′j′k ′l ′ = 0
再由置换知, 2 3 1 再由置换知,、、任意一个数值 如在下标中只出现单数 次,则该项 Aijkl = 0。
A11 A21 A 31
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《连续介质力学》例题和习题第一章 矢量和张量分析第一节 矢量与张量代数一、矢量代数令112233A A A =++A e e e ,112233B B B =++B e e e ,则有112233A A A αααα=++A e e e111222333()()()A B A B A B +=+++++A B e e e112233112233112233()()A A A B B B A B A B A B •=++•++=++A B e e e e e e112233112233111112121313212122222323313132323333()() A A A B B B A B A B A B A B A B A B A B A B A B ⨯=++⨯++=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯A B e e e e e e e e e e e e e e e e e e e e e e e e又因为: 11⨯=e e 0;123⨯=e e e ;132⨯=-e e e ;213⨯=-e e e ;22⨯=e e 0;231⨯=e e e ; 312⨯=e e e ;321⨯=-e e e ;33⨯=e e 0则: 233213113212213(_)()()A B A B A B A B A B A B ⨯=+-+-A B e e e 习题:1、证明下列恒等式:1)[]2()()()()⨯•⨯⨯⨯=•⨯A B B C C A A B C2) [][]()()()()⨯•⨯=•⨯-•⨯A B C D A C D B B C D A2、请判断下列矢量是否线性无关?1232=-+A e e e 23=--B e e 12=-+C e e .其中i e 为单位正交基矢量。
3、试判断[]816549782-⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦A 是否有逆矩阵;如有,请求出其逆阵[]1-A 。
二、张量代数例1:令T 是一个张量,其使得矢量a ,b 经其变换后变为2=+Ta a b ,=-Tb a b ,假定一个矢量2=+c a b ,求Tc 。
解:利用张量的线性性质,有:(2)=+Tc T a b =()22(2)2(2)33+=+=++-=+Ta Tb a b a b a b a b例2:假定一个张量T 将基矢变换成以下形式:1123212331232643422=-+=+-=-++Te e e e Te e e e Te e e e那么该张量T 将12323=++a e e e 变换成什么样的结果? 解:由T 对基矢量的变换张量可知T 的矩阵表示为:232641412ij -⎡⎤⎢⎥⎡⎤=-⎣⎦⎢⎥⎢⎥-⎣⎦T则有:232126412541238-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦Ta b即123258=++b e e e例3:利用张量的变换定义证明:1)若ij T 为一个二阶张量,则ij kl T T 为一四阶张量;2)若i a 为一矢量,则对任意坐标系满足i ij j a T b =的i b 为一矢量。
证明:1)因为ij T 为一二阶张量,由张量的变换定义有:ij mi nj ij T Q Q T '= klrk sl rs T Q Q T '= 则有 ij klmi nj ij rk sl rs mi nj rk sl ij rs T T Q Q T Q Q T Q Q Q Q T T ''== 令ijkl ij kl M T T '''= ijkl ij rs M T T =则有ijklmi nj rk sl ijkl M Q Q Q Q M '= 即M 为一四阶张量。
2)由于i a 和ij T 分别是矢量和张量,则有i im m a Q a '= ij im jn mn T Q Q T '= 由此可得:im mim jn mn j Q a Q Q T b ''= (*) 又因为i ij j a T b =对于任意坐标系都成立,则有i ij j a T b '''= mmn n a T b '''= 由(*)式可得:im mnn im jn mn j Q T b Q Q T b '''= 等式两边同时乘以ik Q 可得: ik im mn n ik im jn mn j Q Q T b Q Q Q T b '''= 又因为ik im km Q Q δ= ,则km mnn km jn mn j T b Q T b δδ'''= 或 kn n jn kn j T b Q T b '''= 所以 ()0knn kn j T b T b '''-= 由于上式对任一张量T 都成立,则有0nkn j b T b ''-= 即n kn j b T b ''= 这即是矢量的定义所满足的方程变换,因此i b 是一个矢量的分量。
习题1、证明:如果ij T 和ij E 为任意二阶张量T 和E 的分量,且ij ijkl kl T C E =对任意坐标系都成立,则ijkl C 为一四阶张量。
例4:已知张量T 的矩阵形式为:200034043ij T ⎡⎤⎢⎥⎡⎤=⎣⎦⎢⎥⎢⎥-⎣⎦,求张量T 的特征值和特征向量。
解:由求特征值和特征向量的特征方程有:()()2200342250043λλλλλλ-⎡⎤⎢⎥-=-=--=⎢⎥⎢⎥--⎣⎦T I 由此,可得三个不同的特征值:12λ= 25λ= 35λ=- 对12λ=,由()0ij ij i T λδα-=可得: (i α为待求的特征向量)100α= 2340αα+= 23450αα-=利用2221231ααα++=可解得:230αα== 11α=±则与12λ=对应的特征向量为:11=±n e对于25λ=,同理有:130α-= 23240αα-+= 23480αα-=同样利用2221231ααα++=可解得:10α=2322αα==±则与25λ=对应的特征向量为:()22312=±+n e e同理,35λ=-对应的特征向量为:)3232=±-+n e e习题:1、令一张量T 可用矩阵形式540410003ij T ⎡⎤⎢⎥⎡⎤=-⎣⎦⎢⎥⎢⎥⎣⎦表示,则: a)求T 的主值和主方向; b)求T 的主不变量;c)如果1n 、2n 、3n 是T 的主方向,则写出[]in Td)针对同样的基矢量,矩阵720210001ij S ⎡⎤⎢⎥⎡⎤=⎣⎦⎢⎥⎢⎥-⎣⎦能否表示同样的张量T ?2、令T 和S 是任意两个张量,试证明:a)TT 是一个张量; b)()T T T +=+T S T S ;c )()T T T=TS S T3、令一张量T 的矩阵形式为:123456789ij T ⎡⎤⎢⎥⎡⎤=⎣⎦⎢⎥⎢⎥⎣⎦,则: a)求张量T 的对称部分和反对称部分; b)求T 的反对称部分的对偶矢量(或轴矢量)。
第二节 矢量和张量的分析例1:利用指标定义证明下列等式:1))r r ∇=r(,r =r2)2)p p r pr -∇=(r ,p 是整数;3))F ∇⨯∇=(0,F 为任一标量函数。
证明:(1)对于任意矢量≡r x,有r ===r 。
则 ()()11122)2i i j j i i i j j i ir r x x x x x x x x r r --∂∂∇==⋅===∂∂r x (e e e由此也可得: iix r x r ∂=∂(2)对()122)pp p p p i i i ii ir r r pr pr x pr x x ---∂∂∇====∂∂(e e e r(3)因为2) =i j ijk k i j i j F FF x x x x ε⎛⎫⎛⎫∂∂∂∇⨯∇=⨯ ⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭(e e e且2i j Fx y ∂∂∂关于i 和j 对称,则对于该矢量的第k 个分量有22ijk k jik ki j i j F F x x x x εε∂∂=-∂∂∂∂e e (i ,j 互换) 2 =-ijk kj iFx x ε∂∂∂e (重新将i 变为j ,j 变为i )2 =-ijk ki j Fx x ε∂∂∂e (利用其对称性)则 )F ∇⨯∇=(0例2:证明()det det T-∂=∂A A A A证明:令B 为任一二阶张量,则有:()()()()11det det =det det ααλαλ--⎡⎤+=--⎣⎦A B A A B I A A B I 其中 1λα=-;因为3det()det()αα=A A结合二阶张量1-A B 的主不变量的定义可得:()()()()()()1321111223111132det 111 =+ I I I I I λλλλααα-------=-+-++A B I A B A B A B A B A B这表明:()()()()()()()()12112313det det det det +det I I I αααα---+=++A B A A A B A A B A A B由张量的标量函数导数的定义有:()0det :det dd ααα=∂=+∂A B A B A (对任一二阶张量B )则 ()()11det :det I -∂=∂A B A A B A又因为: ()()111:TI tr ---==A B A B A B 则有 ()det :(det ):T-∂=∂A B A A B A由B 的任意性可得:()det (det )T -∂=∂AA A A习题1、令V 和W 为矢量场,φ为标量场,证明下列不等式: a )()0∇∇⨯=Vb )()()()∇⨯=∇⨯-∇⨯V W W V V Wc )()()∇⨯∇⨯=∇∇-∆V V V (()∆=∇∇V V )d ) ()0φ∇⨯∇=2、对于():tr ψ=A A A B ,其中B 为一常值二阶张量,证明:()():ψ∂=+∂AA B I tr A B A3、考虑一张量值函数()2∑=A A ,证明:()∂∑=+∂A B BA AB A (其中B 为一任意二阶张量)第二章 运动学第一节 物体的运动例1:考虑如下运动:21ktX =+x X e ,其中112233x x x =++x e e e 是质点P 在t 时刻的位置矢量,而112233X X X =++X e e e 是质点P 在t =0时刻的位置矢量。
