2016新编哈工大材料力学上机大作业四——绘制梁的剪力弯矩图
作此梁的剪力图和弯矩图

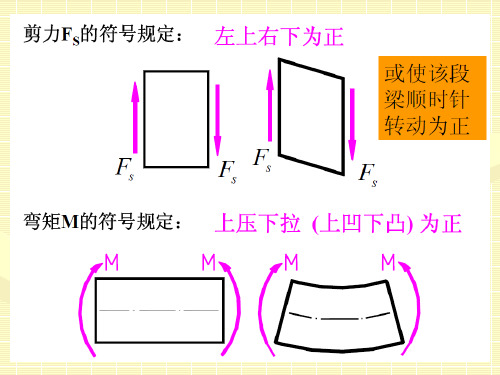
• 弯矩为正时,正应力 以中性轴为界下拉上 压;
• 弯矩为负时,正应力上拉下压;
M
• 中性轴上,正应力等于零
3、静力学关系分析
没有轴向力 dA 0 A
E E y
E
E
A ydA A ydA 0
质心坐标
A ydA 0
ydA A
yc A
l
2
集中力使弯矩图折曲
(3)画弯矩图
集中力偶使弯矩图突变
5、分布载荷q、剪力Q 和弯矩 M之间的微分
关系
Y 0 :
Q qdx Q dQ 0
M0 0:
M Qdx qdx dx M dM 0
2
dQ qdx dM Qdx
dQ q , dx
斜的直线。此时弯矩图曲线的开口向下,具有极大值,极 值点位于剪力Q 为零的截面。
(4)集中力使剪力图突变,集中力偶矩使弯矩图突变。(突变 值等于集中力或集中力偶矩的值)
q 1 kN / m P1 2 kN
M D 10 kNm
P2 2 kN
A
C
D
RA
4m
4m
B
RB
4m
3m
E
RA 7 kN RB 5 kN
hb3 12
圆形与圆环截面
I p
A
2dA
D4
32
IP
2dA
A
( y2 z2 )dA A
y2dA
A
A z2dA Iz I y
IP 2Iz 2Iy
实心圆
Iz
Iy
材料力学4-弯矩图剪力图 PPT课件
梁上最大弯矩可能发生在Fs(x) = 0 的截面上或梁段边界 的截面上。最大剪力发生在全梁或梁段的界面。
在集中力作用处剪力图有突变,其突变值等于集中力的 值。弯矩图的相应处形成尖角。
在集中力偶作用处弯矩图有突变,其突变值等于集中力 偶的值,但剪力图无变化。
矩就等于梁在各项荷载单独作用下同一 横截面上弯矩的代数和。
叠加原理:由几个外力共同作用时所引起的某一参数 (内力、应力、位移),就等于每个外力单独作用时 所引起的该参数值的代数和。
• 5.4 内力与分布荷载间的关系及其应用
剪力图上某点处的切线斜率 等于该点处荷载集度的大小
弯矩图上某点处的切线斜率 等于该点处剪力的大小。
q(x)、Fs (x)图、M(x)图三者间的关系
梁上有向下的均布荷载,即 q(x) < 0 Fs (x)图为一向右下方倾斜的 直线 M(x)图为一向下凸的二次抛 物线
• 5.3 剪力方程与弯矩方程 剪力图与弯矩图
一、剪力和弯矩方程: 剪力和弯矩沿梁长度方向的表达式,表示的是剪力和
弯矩沿轴线长度方向的分布情况
二、剪力图和弯矩图 以X轴表示横截面位置,以纵坐标表示相应截面
上的剪力Fs 、弯矩M,称为剪力图、弯矩图。 剪力图为正值画在x 轴上侧,负值画在x 轴下侧 弯矩图为正值画在x 轴下侧,负值画在x 轴上侧
作剪力图和弯矩图的几条规律
梁上集中力作用处左、右两侧横截面上,剪 力值(图)有突变,其突变值等于集中力的 数值。在此处弯矩图则形成一个尖角。
梁上集中力偶作用处左、右两侧横截面上 的弯矩值(图)也有突变,其突变值等于 集中力偶矩的数值。但在此处剪力图没有 变化。
作剪力图和弯矩图的几条规律
梁上的最大剪力发生在全梁或各梁段的边界 截面处;梁上的最大弯矩发生在全梁或各梁 段的边界截面,或Fs = 0的截面处。
弯曲内力—利用内力图规律绘制剪力图和弯矩图(材料力学)
在控制截面处将梁分段,判断各段剪力图和弯矩图的大致形状。
3 求控制截面的内力值
利用计算截面内力的代数和法,求出各控制截面上的Fs和M值。
4 连线绘图
利用荷载、剪力和弯矩之间的微分关系及内力图规律,逐段绘出梁的Fs图和M图。
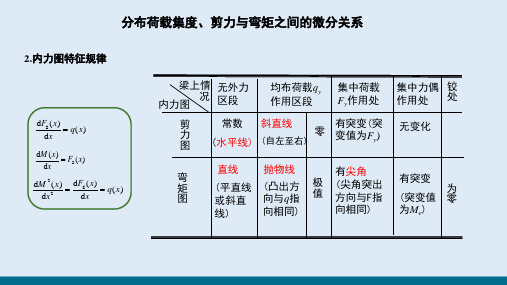
分布荷载集度、剪力与弯矩之间的微分关系
[例1] 利用内力图特征绘制梁的内力图
2
1
3
1m
1.5m
5kN
0.5m
1m 1kN
dFS(x) q(x) dx
dM (x) dx
FS (x)
q=0,FS = 常数,平直线; M(x)为 x 一次函数,斜直线;
q=2kN/m
1.25 1
q常数,FS (x) 为 x 一次函数,斜直线;
M(x) 为 x 二次函数,抛物线;
集中力作用处,剪力图突变。
分布荷载集度、剪力与弯矩之间的微分关系
2.内力图特征规律
dFS(x) q(x) dx
dM (x) dx
FS (x)
dM 2 (x) dx2
dFS (x) dx
q(x)
梁上情 无外力 内力图 况 区段
均布荷载qy 集中荷载
作用区段
Fy作用处
剪 力 图
常数 斜直线
有突变(突
零 (水平线) (自左至右)
qL
q
解: FSA右 qL
A
C
L/2
B L/2
FS
FSC qL
FSB
qL
q
L 2
3 2
qL
MA 0
qL
qL
3qL/2
L MC qL 2
qL2 2
9qL2 /8
[数学]材料力学_弯矩剪力图PPT资料54页
![[数学]材料力学_弯矩剪力图PPT资料54页](https://img.taocdn.com/s3/m/1d47a890c281e53a5802ffa1.png)
aF
b
A
x
C
FA
l
B
FA
Fb l
FB
FB
Fa l
AC段 A
M(x)
FSxFl b0xa
FA
x
FS(x)
MxFxb0xa
l
F Sx F BF l a axlM(x)
MxFB(lx)
Falx
l
FS(x)
axl
CB段 B FB
3、作剪力图和弯矩图
aF
b
A
x
C
FA
l
Fb
FS
l
Fb l
M
FS1x
Fb l
B
a
Me
b
A
B
C
FA
l
FB
解: 1、求支反力
MA0
FA
Me l
M eF A l0
FB
Me l
2、 列剪力方程和弯矩方程
a
b
FA
Me l
A
x
C
FA
l
B
FB
FB
Me l
剪力方程无需分段: M(x)
F SxMF A (x ) M le0xl
A
FA
x
FS(x)
B FS(x) FB
弯CABC矩段段方::程—M M —x 两x 段F F :A Ax x M M lee xM le 0 l x xa a xl
x
Mxqlxqx2
22
FS,max
ql 2
ql 2 ql2 8
M
l/2
Mmax
ql2 8
* 载荷对称、结构对称则剪力图反对称,弯矩图对称
哈工大材力上机大作业解析

材料力学上机报告课程名称:材料力学设计题目:简支梁在任意载荷下剪力图弯矩图挠度曲线的绘制院系:材料学院班级:设计者:学号:编程语言:Visual Basic设计时间:2016.06一、课题要求求三种截面的简支梁(矩形截面,实心圆截面和空心圆截面)在受到任意多的力F,力偶M和分布力q的作用下,其上任意一点的剪力弯矩和挠度的大小,并绘制梁的剪力图、弯矩图和挠曲线。
输入1.梁的总长度l和材料的弹性模量E。
2.选择界面形状(矩形截面,实心圆,空心圆)。
如果是矩形截面,输入矩形的宽度b和高度h。
如果是实心圆截面,输入圆的直径D。
如果是空心圆截面,输入空心圆的外径D和内径d。
3. 输入载荷情况。
若载荷是力,输入力的大小F和作用点a。
如果载荷是均布载荷,输入均布载荷的大小q和载荷的起始位置c和终止位置f。
如果载荷是力偶。
输入力偶的大小m和作用点e。
输出:1. 结构构形图2. 任意一点的剪力,弯矩,挠度3. 画出剪力图,弯矩图和挠曲线二.数学模型及算法总体思想为叠加法。
不妨假设简支梁的长度为l。
1.只有一个作用点位置为a的力F的作用下a)剪力的大小当0<x<a时,f1=(l-a)/l*f当a<x<l时,f1=(-1)*a/l*fb)弯矩的大小当0<x<a时:m1= (l-a)/l*F*x当a<x<l时:m1= a/l*F*(l-x)c)挠度的大小v1=(-1)*(F*(l-a)/(6*E*I*l))*(l/(l-a)*(x-a)^3)+((l*l-(l-a)*( l-a))*x- x^3)2.只有一个作用点位置为b和c的均布力作用下a)剪力的大小当0<x<b时:f2= q*(c-b)*(3*c-b)/(2*l)当b<x<c时:f2= q*(c-b)*(3*c-b)/(2*l)-q*(x-b)当c<x<l时:f2= (-1)*q*(c*c-b*b)/(2*l)b)弯矩的大小当0<x<b时:m2=q*(c-b)*(3*c-b)/(2*l)当b<x<c时:m2= q*(c-b)*(3*c-b)/(2*l)-(q*(x-b)*(x-b))/2当c<x<l时:m2= (-1)*(q*(c*c-b*b)/(2*l))*(c-x)c)挠度的大小当0<x<b时:v2= q*(c-b)*(3*c-b)/(12 *E*I*l)* (x^3)当b<x<c时:v2=q*(c-b)*(3*c-b)/(2*l)* (x^3)/6-((q*(x-b)*(x-b))/4) * (x^2)当c<x<l时:v2= (-1)*(q*(c*c-b*b)/(4 *E*I*l))*(c-x)* (x^2)3.只有一个作用点位置为d的力偶的作用下a)剪力的大小f3=m/lb)弯矩的大小当0<x<d时:m3= m/l*x当d<x<l时:m3= (-1)*m/l*(l-x)c)挠度的大小v3= (-1)*m/(6*E*I*l)*((-1)* (x^3)+3*l* ((x-d)^2)+x*(l*l-3* ((l-d)^2)))其中惯性矩I分为三种情况,即实心圆,空心圆和矩形截面:实心圆:I= pi*(d^4)/64空心圆:I= pi*(D^4) *(1- ((d/D)^4)/64矩形截面:I= b* (h^3)/12三.程序流程图三.程序变量说明及程序清单E:弹性模量n:力的个数F:集中力大小c:分布力右端距左端支座的距离k:空心圆筒内径o:空心圆筒外径L:杆件长度G:切变模量b:矩形截面的宽度h:矩形截面的高Y:挠度jiao:转角I:截面惯性矩L:梁长E:弹性模量Z:惯性矩a:集中力距支座左端的距离d:实心圆径q:分布力大小M:力偶大小程序源代码Form 1(封皮)Private Sub Command1_Click() '点击简支梁,出现form2Form1.HideForm10.ShowPrivate Sub Command2_Click() '点击结束,结束整个程序EndEnd SubPrivate Sub Form_Load()Label1.FontBold = TrueEnd SubForm10开始进入选择阶段(剪力弯矩或者挠度)Private Sub Command1_Click() '梁剪力弯矩图Form3.ShowForm2.HideEnd SubPrivate Sub Command2_Click() '梁挠度Form2.ShowForm3.HideEnd SubPrivate Sub Form_Load()End SubPrivate Sub Frame1_DragDrop(Source As Control, X As Single, Y As Single)Private Sub Option1_Click() '矩形数据的输入Text8.Enabled = FalseText6.Enabled = TrueText7.Enabled = TrueText11.Enabled = FalseText12.Enabled = FalsePicture4.Visible = TruePicture5.Visible = FalsePicture6.Visible = FalseEnd SubPrivate Sub Option2_Click() '圆截面数据的输入Text8.Enabled = TrueText6.Enabled = FalseText7.Enabled = FalseText11.Enabled = FalseText12.Enabled = FalsePicture4.Visible = FalsePicture5.Visible = TruePicture6.Visible = FalseEnd SubPrivate Sub Option3_Click() '空心圆截面数据的输入Text8.Enabled = FalseText6.Enabled = FalseText7.Enabled = FalseText11.Enabled = TrueText12.Enabled = TruePicture4.Visible = FalsePicture5.Visible = FalsePicture6.Visible = TrueEnd SubPrivate Sub Text1_Change() 'F的单位换算F = Val(Text1.Text) * 1000End SubPrivate Sub Text11_Change() '对o赋值,并换算o = Val(Text11.Text) / 100End SubPrivate Sub Text12_Change() '对d赋值,换算,并计算空心圆截面的Iz的值k = Val(Text12.Text) / 100F = (k / o) ^ 4Iz = 3.1415926 * o ^ 4 / 64 * (1 - F)End SubPrivate Sub Text2_Change() 'a的单位换算a = Val(Text2.Text) / 100End SubPrivate Sub Text3_Change() 'M的单位换算M = Val(Text3.Text) * 1000End SubPrivate Sub Text5_Change() 'q的单位换算q = Val(Text5.Text) * 1000End SubPrivate Sub Text6_Change() '对b赋值b = Val(Text6.Text)End SubPrivate Sub Text7_Change() '对h赋值,并计算矩形截面的Iz的值h = Val(Text7.Text)Iz = 10 ^ -8 * h * b ^ 3 / 12End SubForm 2 (输入杆长,载荷和截面大小尺寸,并且选择所要求的挠度,挠曲线等)Private Sub Check1_Click() '显示待输入数据栏及力样图片Text1.Enabled = TrueText2.Enabled = TruePicture3.Visible = TruePicture1.Visible = FalsePicture2.Visible = FalseEnd SubPrivate Sub Check2_Click() '显示待输入数据栏及力样图片Text3.Enabled = TruePicture1.Visible = FalsePicture2.Visible = TruePicture3.Visible = FalseEnd SubPrivate Sub Check3_Click() '显示待输入数据栏及力样图片Text5.Enabled = TruePicture1.Visible = TruePicture2.Visible = FalsePicture3.Visible = FalseEnd SubPrivate Sub Command1_Click() '返回主菜单,并清空数据Text1.Enabled = False: Text2.Enabled = False: Text3.Enabled = False: Text5.Enabled = False: Text8.Enabled = False:Text12.Enabled = False: Text11.Enabled = False: Text6.Enabled = False: Text7.Enabled = FalseCheck1 = False: Check2 = False: Check3 = False: Option1 = False: Option2 = FalsePicture1.Visible = False: Picture2.Visible = False: Picture3.Visible = False: Picture4.Visible = False: Picture5.Visible = FalseIz = 0: E = 0: Ym = 0: jiaom = 0: L = 0: F = 0: M = 0: q = 0: a = 0: b = 0: h = 0: d = 0: X = 0Text1.Text = "": Text2.Text = "": Text3.Text = "": Text8.Text = "": Text5.Text = "": Text6.Text = "": Text7.Text = "": Text9.Text = "": Text10.Text = ""Form2.HideForm10.ShowForm3.HideEnd SubPrivate Sub Command2_Click() '最大挠度与转角的输入检测If L = 0 Or E = 0 Or Iz = 0 Thenn = MsgBox("您还有数据未输入。
材料力学 静定外伸梁的剪力图和弯矩图 解题过程

画出下面梁的剪力图和弯矩图。
1.问题分析:属于受集中力、均布力的外伸梁,静定梁。
2.将A点的固定支座去掉,以F AX、F Ay代替支座反力。
将B点的滑动支座去掉,以F B代替支座反力,如下图所示。
利用静力平衡方程求解如下:∑F x=0,得出:F AX=0(1)∑F Y=0,得出:F AY+F B=30+20×2+40(2)∑M B=0,得出:−30×6+F AY×4−20×2×1+40×2=0(3)由方程(1)、(2)、(3)解得:F AY=35kN,F B=75kN3.剪力图求解出未知的支座反力后,梁的受力如下图所示。
如果认为剪力比较简单,可直接画出剪力图。
如果直接画出有些困难,可以分段列出梁的剪力方程,根据每段的剪力方程,分段画出剪力图。
剪力的正负按照“左上右下,剪力为正”来判断。
剪力方程如下:CA段:F s1=−30kN 0<x≤2AE段:F s2=−30+35=5kN2≤x≤4EB段:F s3=−30+35−20×(x−4)=−20x+854≤x≤6当x=6时,F s3=−35kNBD段:F s4=−30+35−20×2+75=40kN6<x≤84.弯矩图如果认为弯矩比较简单,可直接画出弯矩图。
如果直接画出有些困难,可以分段列出梁的弯矩方程,根据每段的弯矩方程,分段画出弯矩图。
弯矩的正负按照“左顺右逆,弯矩为正”来判断。
弯矩方程如下:CA段:M1=−30x0<x≤2当x=2时,M1=−60kNmAE段:M2=−30x+35(x−2)=5x−702≤x≤4当x=4时,M2=−50kNmEB段:M3=−30x+35(x−2)−20×(x−4)×x−42=−10x2+85x−2304≤x≤6对上式求“最大值点”,以便画弯矩图。
当x=4.25时,M3max=−49.375kNmBD段:M4=−30x+35(x−2)−20×2×(x−5)+75×(x−6)=40x−3206<x≤8此段的弯矩图也可由右侧的剪力直接画出。
材料力学上机作业绘制梁的剪力弯矩图
H a r b i n I n s t i t u t e o f T e c h n o l o g y材料力学上机作业课程名称:材料力学设计题目:绘制梁的剪力弯矩图院系:机电工程学院班级:分析者:学号:指导教师:张桂莲设计时刻: 2021.6.3哈尔滨工业大学一、设计题目题目4 绘制梁的剪力弯矩图输入:1.梁的总长度l2.支撑条件及量的各区段长度输入(左、右固定端悬臂梁;简支梁;左、右、双外伸梁)3.各载荷大小、作用位置及方向(qi、ai、bi;pj、cj、mk、dk)输出:1.结构构型图(图示)2.剪力、弯矩(图示)3.输出剪力、弯矩的最大值及截面位置。
二、程序介绍一、简介本程序编译平台为MATLAB,能够对六种梁(左固定端悬臂梁、右固定端悬臂梁、简支梁、左外伸梁、右外伸梁、双外伸梁)在集中载荷、均布载荷及弯矩作用下的剪力、弯矩进行求解并绘制剪力、弯矩图。
本程序基于MATLAB的图形用户界面(GUI)功能,操作简单、运算稳固、界面简约美观,有良好的交互性。
二、程序利用方式此程序运行环境为安装有MATLAB R2020a或以上版本的运算机。
要运行此程序,第一打开MATLAB,在其中打开“KaiShiJieMian.m”文件,在函数编辑窗口里点击运行按钮(或按F5键),程序便开始启动。
启动画面如下:图1 启动界面点击“进入”即可进入选择梁的类型界面,在此界面中,利用者依如实际情形选择要研究的梁的类型,点击即可进入相应梁的计算界面。
例如想要计算双外伸梁,那么点击“6、双外伸梁”即可进入计算界面,假假想返回开始界面,那么点击“返回开始界面”即可。
图2 梁的选择界面图3 梁的计算界面此程序能够计算梁在集中力、均布力和集中力偶的作用下梁的剪力和弯矩,并求出剪力的最大值和弯矩的最大值。
以双外伸梁为例,对照左侧参数输入提示,在相应文本框里输入梁的大体参数,如弹性模量E、长度L,和载荷大小及位置,如均布力q、均布力起始位置b1、终止位置b2。
哈工大材料力学计算机计算大作业_范例
B
ql 3 48 EI z
500 23 1.5215mrad 3 0.034 0.054 3 9 0.04 0.06 48 200 10 12 12 500 2 4 1.1411mm 3 0.034 0.0543 9 0.04 0.06 128 200 10 12 12
max
1000 32 1 5.77 mm , x 3 1732.1mm 9 3 100000 3
电算解:
故:与理论解一致。
第 十四 页 共 二十一 页
材料力学大作业
(8)理论解:
增补条件: 代入约定条件算得: A M 3000 N m , a 1 .6 m , 电算解:
3
电算解:
故:与理论解一致。
第 十七 页 共 二十一 页
材料力学大作业
(11)理论解:
代入约定数据解之得: A B 11 .25mrad ; C
5 1000 34 10.55mm 384 100000
电算解:
故:与理论解一致。
第 十八 页 共 二十一 页
然后,我们需要输入抗弯刚度。题目没有给怎么办?不怕,我们有“抗弯刚度计算器”!点击对 应区段抗弯刚度边上的按钮即可开始计算!
第 三 页 共 二十一 页
材料力学大作业
在计算完毕之后,点击“置入并返回” ,则我们又来到了基本信息输入界面。由于这一根简单 梁是等截面、等抗弯刚度的,所以我们不用去管“区段二”和“区段三”的相关文本框(实际上在 你选定对应的区段之前,这些文本框都是无法激活的) 。我们需要点击“更新基本信息”按键,以 核查、写入数据。核查无误,我们点击“受力情况输入”按钮。
《材料力学》中剪力图和弯矩图的快易绘图法
《材料力学》中剪力图和弯矩图的快易绘图法[摘要]在《材料力学》中,绘制平面弯曲梁的剪力图和弯矩图是“直梁的弯曲”一章中的重点和难点,传统的规律绘图法用到的一次函数、二次函数和导数等相关知识,对于数学基础不很扎实的中专生来说是很难理解的。
本文中作者利用几何图形的面积来绘制剪力图和弯矩图,其方法更为简便快捷。
[关键词]剪力图弯矩图面积在《材料力学》中,直梁的弯曲变形是杆件受力变形的基本形式之一,在对梁进行强度和刚度计算时,通常要画出剪力图和弯矩图(即把剪力方程和弯矩方程用函数图象表示出来)以便清楚地看出梁的各个截面上剪力和弯矩的大小、正负以及最大值所在截面的位置。
目前绘制剪力图和弯矩图最常用的规律绘图法中用到一次函数、二次函数和导数等相关知识,这对于数学基础不很扎实的中专生来说是很难理解的。
通过教学,作者在原有绘图方法的基础上,利用几何图形的面积代替一次函数、二次函数和导数来绘制剪力图和弯矩图的规律,谨供广大同仁参考。
具体方法为:从上至下依次画出直梁的受力分析图——剪力图(直角坐标系)——弯矩图(直角坐标系),其图象遵循“平行线——斜直线——抛物线”的顺序,其剪力和弯矩的变化值等于对应的上一个几何图形的面积,其它事宜与原方法同。
例:一外伸梁受力如图a)所示,已知P=6kN,q=2kN/m,a=1m,绘出梁的剪力图和弯矩图。
解:(1)求支座反力NA和MA选整个梁为研究对象,由平衡方程求得NA= 10kN,MA= 18kN.m。
(2)绘制剪力图A点作用有向上的集中载荷NA和逆时针转向的集中力偶MA,因集中力偶对剪力图没有影响,故剪力图只在集中力NA的作用下从零值向上突变10 kN;A、B点之间的剪力图为平行于x轴的直线;B点作用有向下的集中力P,剪力图向下突变P=6kN,变为4 kN;B、C之间的剪力图为平行于x轴的直线;CD 段作用有向下的均布载荷q=2kN/m,所以剪力图为从4 kN开始向下倾斜的直线,因此D点剪力值为4 kN -4 kN=0,如图b)所示。
材料力学第五章梁的剪力图与弯矩图
29
§5-3
剪力和弯矩及其方程
为了建立剪力方程和弯矩方程,必须首先 建立Oxy坐标系。其中O为坐标原点,x坐 标轴与梁的轴线一致,坐标原点O一般取 在梁的左端,x坐标轴的正方向自左向右, y坐标轴铅垂向上。
30
§5-3
剪力和弯矩及其方程
建立剪力方程和弯矩方程,需要根据梁上的外 力(包括载荷和约束力)作用状况,确定控制 面,从而确定要不要分段,以及分几段建立剪 力方程和弯矩方程。
FBy
F 0 M 0
y A
FAy FBy 2F
FSE O FAy ME
FBy
F 5F FAy 3 3
分析右段得到:
FBy
O
ME FSE
F
FBy
y
0
FSE FBy 0
M
o
0
3a M E FBy Fa 2
27
§5-3 剪力和弯矩及其方程
F FBy 3
3、平面弯曲(对称弯曲):若梁上所有外力都作用在纵向对称面内,
梁变形后轴线形成的曲线也在该平面内的弯曲。
4、非对称弯曲:若梁不具有纵向对称面,或梁有纵向对称面上但外力
并不作用在纵向对称面内的弯曲。
13
工程实际中的弯曲问题简图
P
P P P
P P P
P
14
平面弯曲
•具有纵向对称面 •外力都作用在此面内 •弯曲变形后轴线变成对称面内的平面曲线
M M M
M
弯矩为正
弯矩为负
22
梁的控制面
集中力作用点两侧的截面
集中力偶作用点两侧的截面 集度相同的均布载荷起点和终点截面处
23
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H a r b i n I n s t i t u t e o f T e c h n o l o g y材料力学上机作业课程名称:材料力学设计题目:绘制梁的剪力弯矩图院系:班级:分析者:学号:指导教师:设计时间:哈尔滨工业大学材料力学上机课设计说明书一,设计题目题目4 绘制梁的剪力弯矩图输入:1.梁的总长度l2.支撑条件及量的各区段长度输入(左、右固定端悬臂梁;简支梁;左、右、双外伸梁)3.各载荷大小、作用位置及方向(q i、a i、b i;p j、c j、m k、d k)输出:1.结构构型图(图示)2.剪力、弯矩(图示)3.输出剪力、弯矩的最大值及截面位置。
二,方向规定本程序规定集中作用力及均布载荷以向下为正,右固定端悬臂梁与左外伸梁集中力偶以顺时针方向为正,其他情况集中力偶以逆时针方向为正。
当取出梁的一段为研究对象时,梁左端面力以向下为正,力偶以顺时针方向为正,梁右端面力以向上为正,力偶以逆时针方向为正。
三,程序设计过程1,制作程序框架,显示提示内容,提示操作者需要输入的作用条件及各作用位置;2,编写程序使计算机读入操作者输入的作用条件;3,草稿拟写各种情况下为达到题目要求所需使用的计算公式设量的长度为l,集中力大小为p,作用位置为c,集中力大小为q,作用起始位置a,终止位置为b,集中力偶大小为m,作用位置d。
(1)左固定端悬臂梁:在任意位置x处,取x以右部分为研究对象a,终止位置为b,集中力作用位置为c,大小为P,集中力偶作用位置为d,大小为m。
①若c<x,a<b<x,d>x,则Fs y=0,M(x)=m;②若c>x,a<b<x,d<x,则Fs y=-P,M(x)=Px-Pc;③若c<x,a<x<b,d<x,则Fs y=-q(b-x),M(x)=-2q(b-x)²;④若c<x, x<a<b,d>x,则Fs y=-q(b-a),M(x)=-q(b-a)(2ba+-x);⑤若c>x,a<b<x,d>x,则Fs y=-P,M(x)= Px-Pc+m;(第①、②两种情况合成)⑥若c<x,a<x<b,d>x,则Fs y=-q(b-x),M(x)=m-2q(b-x)²;(第①、③两种情况合成)⑦若c<x,x<a<b,d>x,则Fs y=-q(b-a),M(x)=m-q(b-a)(2ba+-x);(第①、④两种情况合成)⑧若c>x,a<x<b,d<x,则Fs y=-P-q(b-x),M(x)=Px-Pc-2q(b-x)²;(第②、③两种情况合成)⑨若c>x,x<a<b,d<x,则Fs y=-P-q(b-a),M(x)=Px-Pc-q(b-a)*(2ba+-x);(第②、④两种情况合成)⑩若c>x,x<a<b,d>x,则Fs y=-P-q(b-a), M(x)=m+Px-Pc-q(b-a)*(2ba+-x);(第①、②、④两种情况合成)⑪c>x,a<x<b,d>x, 则Fs y=-P-q(b-x), M(x)m+Px-Pc-q(b-a)*(2ba+-x); (第①、②、③两种情况合成)将上述公式编入程序即可计算出在固定端悬臂梁情况下任意位置处的剪力和弯矩,采用散点法作出梁的剪力弯矩图。
利用max函数筛选出最大值及该最大值所对应的x,即可输出最大值和最大值位置。
(2)右固定端悬臂梁:在任意位置x处,取x以左部分为研究对象分析方法与(1)相同,但注意此时规定的集中力偶正方向与(1)相反(程序中已注明),仍采用散点法和max函数即可求得剪力弯矩图以及剪力弯矩的最大值与其出现位置。
(设梁的总长度为l,均布载荷起始位置为a,终止位置为b,集中力作用位置为c,大小为P,集中力偶作用位置为d,大小为m。
首先对于图示情况求支反力:∑M A=0,q(b-a)*(a+2a-b)+P*c-m+F B*l=0 ∑M B=0,q(b-a)*(i-a-2a-b)+P*(l-c)+m-FA*l=0解得:F A=[q(b-a)(l-2a-b)+ P*(l-c)+m]/l FB=2l22?-²(mPcabq-+由于F B的表达是相对于F A较简单一些,所以以A点为原点建立坐标系,并取出任意位置x以右部分为研究对象,分类如下:①若c<x,a<b<x,d>x,则Fs y= F B,M(x)=m+ F B(l-x);②若c>x,a<b<x,d<x,则Fs y= F B-P,M(x)= F B(l-x)+Px-Pc;③若c<x,a<x<b,d<x,则Fs y= F B -q(b-x),M(x)= F B(l-x)-2q(b-x)²;④若c<x,x<a<b,d>x,则Fs y=F B-q(b-a),M(x)=F B(l-x)-q(b-a)*(2ba+- x);⑤若c>x,a<b<x,d>x,则Fs y= F B -P,M(x)= F B(l-x)+Px-Pc+m;⑥若c<x,a<x<b,d>x,则Fs y= F B-q(b-x),M(x)= F B(l-x)+m-2q(b-x)²;⑦若c<x,x<a<b,d>x,则Fs y=F B-q(b-a),M(x)=F B(l-x)+m-q(b-a)*(2ba+-x);⑧若c>x,a<x<b,d<x,则Fs y=F B-P-q(b-x),M(x)=F B(l-x)+Px-Pc-2q(b-x)²;⑨若c>x,x<a<b,d<x,则Fs y=F B-P-q(b-a),M(x)=F B(l-x)+Px-Pc-q(b-a) *(2ba+-x);⑩若c>x,x<a<b,d>x,则Fs y=-F B+P-q(b-a), M(x)=F B(l-x)+m+Px-Pc-q(b-a) *(2ba+-x);⑪c>x,a<x<b,d>x, 则Fs y=F B-P-q(b-x), M(x)=F B(l-x)+m+Px-Pc-q(b-a) *(2b a +-x); 将上述公式编入程序即可计算出在简支梁情况下任意位置处的剪力和弯矩,采用散点法作出梁的剪力弯矩图。
利用max 函数筛选出最大值及该最大值所对应的x ,即可输出最大值和最大值位置。
(4)右外伸梁程序编写:设梁的总长度为l,可动铰支座位置在s2处,均布载荷起始位置为a ,终止位置为b ,集中力作用位置为c ,大小为P ,集中力偶作用位置为d ,大小为m 。
以梁最左端为原点、向右为正方向作x 轴,设右边可动铰支座距远点距离为s,则可求得支反力:∑M A =0, F B *s+m-q*(b-a)*(a+2a -b )-Pc=0 ∴F B =2s 2m -a?-²(Pc 2b q + F A =s m a b s a b q c s 22)2)(()(P 2+---+- 1)对集中力P 作用情况进行分类讨论当只有集中力作用时,∑M A =0,F B*s-Pc=0, ∴F B =s Pc F A =sc)-P(s ①c>s ,对任意位置x 处有若0≤x<s ,则Fs y '=-F A ,M(x)'=F A *x ;若s ≤x ≤c ,则Fs y '=-P ,M(x)'=P x-P c ;若c ≤x ≤l ,则Fs y '=0,M(x)'=0;②c ≤s ,对任意位置x 处有若0≤x<s ,则Fs y '=-F A ,M(x)'=F A *x ;若c ≤x ≤s ,则Fs y '=P-F A ,M(x)'=F A *x-P(x-c);若s<x ≤l ,则Fs y '=0,M(x)'=0;2)对集中力偶m 作用情况进行分类讨论求支反力:F A +F B =0, ∑M A =0,F B*s+m=0, ∴F B =-s m F A =s m ①d>s ,对任意位置x 处有若0≤x ≤s ,则Fs y ''=-s m , M(x)''=sm x ; 若s <x ≤d ,则Fs y ''=0, M(x)''=s m x-s m (x-s)=m ; 若d<x ≤l ,则Fs y ''=0, M(x)''=0;②d ≤s ,对任意位置x 处有若0≤x ≤d ,则Fs y ''=-s m , M(x)''=sm x ; 若d <x ≤s ,则Fs y ''=-s m , M(x)''=s m x-m ; 若s<x ≤l ,则Fs y ''=0, M(x)''=0;3)对均布载荷q 作用情况进行分类讨论当只有均布载荷作用时,求支反力:F A +F B =q(b-a), ∑M A =0,F B*s-q(b-a)(a+2a -b )=0, ∴F B =-2s ))(a (q a b b -+ F A =2sb)-a)(a -q(b ① 当0≤a <b ≤s 时,对任意位置x 处有若0≤x ≤a ,则Fs y '''=-F A , M(x)'''=F A*x ;若a <x <b ,则Fs y '''=-F A +q(x-a), M(x)'''=F A*x-21q (x-a)²; 若b ≤x ≤s ,则Fs y '''=-F A +q(b-a), M(x)'''=F A*x-q(b-a)(x-2b a +); 若s <x ≤l ,则Fs y '''=0, M(x)'''=0;② 当0≤a <s ≤b 时,对任意位置x 处有若0≤x ≤a ,则Fs y '''=-F A , M(x)'''=F A*x ;若a <x <s ,则Fs y '''=-F A +q(x-a), M(x)'''=F A*x-21q (x-a)²; 若s ≤x ≤b ,则Fs y '''=-q(b-x), M(x)'''=21q(b-x)²;若b <x ≤l ,则Fs y '''=0, M(x)'''=0;③ 当0≤s ≤a<b 时,对任意位置x 处有若0≤x ≤s ,则Fs y '''=-F A , M(x)'''=F A*x ;若s <x <a ,则Fs y '''=-q(b-a), M(x)'''=q(b-a)(x-2b a ); 若a ≤x ≤b ,则Fs y '''=-q(b-x), M(x)'''=-21q(b-x)²;若b <x ≤l ,则Fs y '''=0, M(x)'''=0;最后采用叠加法Fs y =Fs y '+Fs y ''+Fs y ''',M(x)=M(x)'M(x)''+M(x)'''(5)左外伸梁程序编写:分析方法与(4)相同,但注意此时规定的集中力偶正方向与(4)相反(程序中已注明),仍采用散点法和max 函数即可求得剪力弯矩图以及剪力弯矩的最大值与其出现位置。
