数学理卷·2014届山东省青岛开发区一中高三12月月考(2013.12)
2014届高三年级12月月考 数学试题
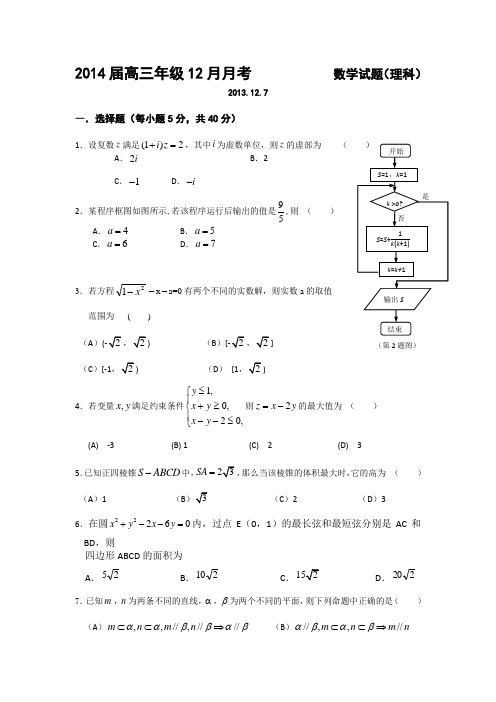
2014届高三年级12月月考 数学试题(理科)2013.12.7一.选择题(每小题5分,共40分)1.设复数z 满足(1)2i z +=,其中i 为虚数单位,则z 的虚部为 (A .2iB .2C .1-D .i -2.某程序框图如图所示,若该程序运行后输出的值是59,则 ( ) A .4=a B .5=aC .6=aD .7=a3.若方程21x--x -a=0有两个不同的实数解,则实数a 的取值范围为 ( )(A ) (B )] (C )[-1 (D ) [1)4.若变量,x y 满足约束条件1,0,20,y x y x y ≤⎧⎪+≥⎨⎪--≤⎩则2z x y =-的最大值为 ( )(A) -3 (B) 1 (C) 2 (D) 35.已知正四棱锥S ABCD -中,SA =,那么当该棱锥的体积最大时,它的高为 ( )(A )1 (B (C )2 (D )3 6.在圆22260x y x y +--=内,过点E (0,1)的最长弦和最短弦分别是AC 和BD ,则四边形ABCD 的面积为A .25B .210C .D .2207.已知m ,n 为两条不同的直线,α,β为两个不同的平面,则下列命题中正确的是( ) (A ),,//,////m n m n ααββαβ⊂⊂⇒ (B )//,,//m n m n αβαβ⊂⊂⇒(第2题图)(C ),//m m n n αα⊥⊥⇒ (D )//,m n n m αα⊥⇒⊥8.已知圆O 的半径为1,PA 、PB 为该圆的两条切线,A 、B 为两切点,那么PA PB ∙的最小值为( )(A) 3-+(B)3-(C) 4-+ (D)4-+二.填空题(每小题5分,共30分)9.若函数()f x ax b =-的零点是1, 则2()g x bx ax =-的零点是 .10.例6. 某几何体的三视图如图所示,则它的体积为______11.直线2cos 1ρθ=与圆2cos ρθ=相交的弦长为 .12.设f(x)是定义在R 上的奇函数,且当x ≤0时,f(x)=-x 2,若对任意的x ∈[t ,t +2],不等式f(x+t) ≥2f(x)恒成立,则实数t 的取值范围为__ 13.在直角坐标系xOy 中,M 是曲线1C :1,12x t y t =+⎧⎨=-⎩(t 为参数)上任意一点,N 是曲线2C :1cos ,sin x y θθ=-+⎧⎨=⎩(θ为参数)上任意一点,则MN 的最小值为 .14.已知关于x 的方程x 3+ax 2+bx+c=0有三个实数根可作为一个椭圆、一个双曲线、一个抛物线的离心率(抛物线的离心率为1),则1a 1+-b 的取值范围为 三.解答题(共80分)15.(本小题共13分)已知函数2()22sin f x x x =-. (Ⅰ)求函数()f x 的最大值; (II )求函数()f x 的零点的集合。
山东省青岛开发区一中2013届高三12月月考试卷 化学

山东省青岛开发区一中2013届高三12月月考试题化学试题2012.12可能用到的相对原子质量:H 1 C 12 N 14 O 16 Na 23 Mg 24 Al 27 S 32 Cl 35.5I 127 Ba 137第Ⅰ卷(选择题共54分)一、选择题(本题包括23个小题,1—15小题,每题2分,共30分;16—23小题,每题3分,共24分.每小题只有一个选项符合题意;多选或错选,本小题不得分。
)1.下列说法中,正确的是A.增大反应物浓度,平衡正向移动,反应物的转化率一定增大B.正、逆反应速率改变时,平衡一定发生移动C.对于任何可逆反应,使用催化剂只改变反应速率,不影响平衡D.增大体系压强,化学反应速率加快,化学平衡一定正向移动用铂作电极电解500 mL含KNO3和Cu(NO3)2的混合溶液一段时间后,在两极均生成11.2L标准状况下的气体,原溶液中Cu2+的物质的量浓度为(.0.5 mol/L B.2 mol/L C.l mol/L D.无法确定3.(2011新课标∙10)将浓度为0.l mol•L-1 HF溶液加水不断稀释,下列各量始终保持增大的是A.c(H+) B. Ka(HF) C. D.4. 已知在100℃的温度下(本题涉及的溶液温度均为100℃),水的离子积K W=1×10-12.下列说法正确的是 ( )A.0.05 mol/L的H2SO4溶液pH=1B.0.001 mol/L的NaOH溶液pH=11C.0.005 mol/L的H2SO4与0.01 mol/L的NaOH等体积混合,混合液pH为6,溶液显酸性D.完全中和pH=3的H2SO4溶液50 mL,需要pH=11的NaOH溶液50 mL 5.下列有关化学反应速率的说法正确的是()A.用铁片和稀流酸反应制氢气时,可改用98%的浓流酸加快生成氢气速率B.100 mL2mol·L-1的盐酸跟锌片反应,加入适量的氯化钠溶液,反应速率不变C.SO2的催化氧化是一个放热反应,所以升高温度,反应速率减慢D.汽车尾气中NO和CO可以缓慢反应生成N2和CO2,减小压强反应速率减慢6.含等物质的量NaOH的溶液分别用pH为2和3的CH3COOH溶液中和,设消耗CH3COOH溶液的体积依次为V a、V b,,则V a、V b的关系正确的是(A.V a>10 V b B.V a=10 V b C.V b<10V a D.V b>10V a 表示阿伏加德罗常数的值。
山东省青岛市经济技术开发区第一中学高二数学理月考试卷含解析

山东省青岛市经济技术开发区第一中学高二数学理月考试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 命题“若,则”的逆命题是()A.若,则 B.若,则C.若,则 D.若,则参考答案:B2. 2007名学生中选取50名学生参加湖北省中学生夏令营,若采用下面的方法选取:先用简单随机抽样从2007人中剔除7人,剩下的2000人再按系统抽样的方法抽取,则每人入选的概率()A.不全相等 B.均不相等C.都相等,且为D.都相等,且为参考答案:C略3. 设△ABC的三边长分别为a、b、c,△ABC的面积为S,内切圆半径为r,则r=;类比这个结论可知:四面体S-ABC的四个面的面积分别为S1、S2、S3、S4,内切球的半径为R,四面体P-ABC的体积为V,则R=()A. B.C. D.参考答案:C4. 已知变量x与y负相关,且由观测数据算得样本平均数=3,=3.5,则由该观测数据算得的线性回归方程可能是()A.=-2x+9.5 B.=2x-2.4C.=-0.3x-4.4 D.=0.4x+2.3参考答案:A5. 若α、β是两个相交平面,则在下列命题中,真命题的序号为( )①若直线m⊥α,则在平面β内,一定不存在与直线m平行的直线.②若直线m⊥α,则在平面β内,一定存在无数条直线与直线m垂直.③若直线m?α,则在平面β内,不一定存在与直线m垂直的直线.④若直线m?α,则在平面β内,一定存在与直线m垂直的直线.A.①③B.②③C.②④D.①④参考答案:C【考点】命题的真假判断与应用.【专题】综合题;推理和证明.【分析】利用线面垂直的性质定理对四个命题分别分析解答.【解答】解:对于①,若直线m⊥α,如果α,β互相垂直,则在平面β内,存在与直线m平行的直线.故①错误;对于②,若直线m⊥α,则直线m垂直于平面α内的所有直线,则在平面β内,一定存在无数条直线与直线m垂直.故②正确;对于③,若直线m?α,则在平面β内,一定存在与直线m垂直的直线.故③错误;对于④,若直线m?α,则在平面β内,一定存在与直线m垂直的直线.故④正确;故选:C.【点评】本题考查了线面垂直的性质定理的运用判断直线的位置关系;关键是熟练运用定理,全面考虑.6. 把边长为a的正△ABC沿BC边上的高线AD折成60°的二面角,则点A到BC的距离是( )A. aB.C.D.参考答案:D【分析】取中点,连接,根据垂直关系可知且平面,通过三线合一和线面垂直的性质可得,,从而根据线面垂直的判定定理知平面,根据线面垂直性质知,即为所求距离;在中利用勾股定理求得结果.【详解】取中点,连接,如下图所示:为边上的高,即为二面角的平面角,即且平面正三角形为正三角形又为中点平面,平面又平面即为点到的距离又,本题正确选项:【点睛】本题考查立体几何中点到直线距离的求解,关键是能够通过垂直关系在立体图形中找到所求距离,涉及到线面垂直的判定定理和性质定理的应用,属于中档题.7. 在各项为正实数的等差数列{a n}中,其前2016项的和S2016=1008,则的最小值为()A.6 B.4 C.D.参考答案:B【考点】等差数列的前n项和.【分析】根据题意和等差数列的前n项和公式求出a1+a2016=1,由等差数列的性质得a1001+a1016=1,利用“1”的代换和基本不等式求出的最小值.【解答】解:∵等差数列{a n}中,S2016=1008,∴,则a1+a2016=1,即a1001+a1016=1,∵等差数列{a n}的各项为正实数,∴==2+≥2+=4,当且仅当时取等号,∴的最小值是4,故选B.8. 在区间上的最大值是()A. B.0 C.2 D.4参考答案:C略9. 已知等比数列{a n}满足,a3a5=4(a4﹣1),则a2=( )A.2 B.1 C.D.C考点:等比数列的通项公式.专题:等差数列与等比数列.分析:利用等比数列的通项公式即可得出.解答:解:设等比数列{a n}的公比为q,∵,a3a5=4(a4﹣1),∴=4,化为q3=8,解得q=2则a2==.故选:C.点评:本题考查了等比数列的通项公式,属于基础题10. 下面给出一个“直角三角形数阵”:,1,,3……其中每一列的数成等差数列,从第三行起每一行的数成等比数列,且公比相等,则第8行的数之和等于()A. B. 510 C. 256 D.72参考答案:B二、填空题:本大题共7小题,每小题4分,共28分11. 在正方体中,异面直线和所成的角的大小为__________.参考答案:12. 若焦点在x轴上的椭圆的离心率为,则m=参考答案:13. (理,实验班)已知,则不等式x·f(x﹣1)<10的解集为______________。
山东省济南一中2014届高三12月月考数学(理)试题

济南一中2014届高三12月月考数学(理)试题一、选择题:本大题共12小题,每小题5分,共60分。
1. 若全集为实数集R ,集合A =12{|log (21)0},R x x C A ->则= ( )A .1(,)2+∞B .(1,)+∞C .1[0,][1,)2+∞ D .1(,][1,)2-∞+∞2. 若O 为平行四边形ABCD 的中心,14AB e =, 2216,32BC e e e =-等于 ( )A .AOB .BOC .COD .DO3. 下列命题中,真命题是( ) A .0,00≤∈∃x eR x B .22,x R x x >∈∀C .0=+b a 的充要条件是1-=baD .1,1>>b a 是1>ab 的充分条件 4. 已知两条直线01:1=-+y x l ,023:2=++ay x l 且21l l ⊥,则a = ( )A. 31-B .31C .3-D .3 5. 若,2παπ⎛⎫∈⎪⎝⎭,1tan ,sin 47παα⎛⎫+==⎪⎝⎭则( ) A.35 B .45 C .35- D .45- 6. 函数xx x f 2)1ln()(-+=的零点所在的大致区间是 ( )A. )1,0( B .)2,1( C .),2(e D .)4,3(7. 在等比数列{n a }中,若232a a +=,12133a a +=,则2223a a +的值是 ( ) A .94 B .49 C .92 D . 298. 已知实数,x y 满足y x z m y x x y y -=⎪⎩⎪⎨⎧≤+-≤≥如果目标函数,121的最小值为-1,则实数m 等于( )A .7B .5C .4D .39. 已知0a b <<,且1a b +=,则下列不等式中,正确的是 ( ) A .2log 0a > B .122a b-< C .12a b b aa+<D .22log log 2a b +<-10. 已知12F F 、是双曲线)0,0(12222>>=-b a by a x 的两焦点,以线段12F F 为边作正三角形,若双曲线恰好平分正三角形的另两边,则双曲线的离心率是 ( ) A .324+B .213+ C .13- D .13+11. 函数()sin()f x A x ωϕ=+(其中0,||2A πϕ><)的图象如图所示,为了得到()cos 2g x x =的图像,则只要将()f x 的图像 ( ) A.向右平移6π个单位长度 B .向右平移12π个单位长度C .向左平移6π个单位长度 D .向左平移12π个单位长度12. 已知函数()f x 对任意x R ∈都有(6)()2(3)f x f x f ++=,(1)y f x =-的图象关于点(1,0)对称,则=)2013(f ( )A .0B .4-C .8-D .16-第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4小题,每小题4分,共16分。
山东省青岛市2014届高三上学期期中考试 理科数学 Word版含答案

高三数学(理科)练习题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟. 注意事项:1.答卷前,考生务必用2B 铅笔和0.5毫米黑色签字笔(中性笔)将姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上.2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号.答案不能答在试题卷上.3.第Ⅱ卷必须用0.5毫米黑色签字笔(中性笔)作答,答案必须写在答题纸各题目指定区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题.每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集R U =,{|A x y ==,则U C A =A .[0,)+∞B .(,0)-∞C .(0,)+∞D .(,0]-∞ 2.已知命题p 、q ,则“p ∧q 为真”是“p ∨q 为真”的 A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件3.向量1(,tan )3a α= ,(cos ,1)b α= ,且a ∥b ,则cos 2α=A. 13-B. 13C. 79-D. 794.在正项等比数列}{n a 中,369lg lg lg 6a a a ++=,则111a a 的值是 A. 10000 B. 1000 C. 100 D. 105.已知0,a >且1a ≠,函数log ,,x a y x y a y x a ===+在同一坐标系中的图象可能是6.定义运算a b ad bc c d =-,若函数()123x f x x x -=-+在(,)m -∞上单调递减,则实数m 的取值范围是 A .(2,)-+∞B .[2,)-+∞C .(,2)-∞-D .(,2]-∞-7.设x ,y 满足约束条件0023x y x y a≥⎧⎪≥⎨⎪+≤⎩,若目标函数11y z x +=+的最小值为12,则a 的值为A .2B .4C .6D .88.已知33)6cos(-=-πx ,则=-+)3cos(cos πx xA .332-B .332±C .1-D .1±9.下列命题中正确的是A .1y x x =+的最小值是2 B .()4230y x x x=-->的最大值是2-C .224sin sin y x x=+的最小值是4 D .()4230y x x x =--<的最小值是2-10.已知等差数列{}n a 的公差0d >,若12320132013t a a a aa ++++= (*N t ∈),则t = A .2014 B .2013 C .1007 D .100611.设a 、b 都是非零向量,下列四个条件中,一定能使0||||a b a b +=成立的是A .13a b =-B .//a bC .2a b =D .a b ⊥12.已知函数()f x 的导函数图象如图所示,若ABC ∆为锐角三角形,则一定成立的是 A .(cos )(cos )f A f B < B .(sin )(cos )f A f B < C .(sin )(sin )f A f B >D .(sin )(cos )f A f B >第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.13.已知函数12log ,1()24,1xx x f x x >⎧⎪=⎨⎪+≤⎩,则1(())2f f = .14.曲线2sin 0)y x x π=≤≤(与直线1y =围成的封闭图形的面积为 . 15.已知函数()f x 是(,)-∞+∞上的奇函数,且()f x 的图象关于直线1x =对称,当[1,0]x ∈-时,()f x x =-,则(2013)(2014)f f += .16.若对任意x A ∈,y B ∈,(A 、R B ⊆)有唯一确定的(,)f x y 与之对应,称(,)f x y 为关于x 、y 的二元函数. 现定义满足下列性质的二元函数(,)f x y 为关于实数x 、y 的广义“距离”:(1)非负性:(,)0f x y ≥,当且仅当x y =时取等号; (2)对称性:(,)(,)f x y f y x =;(3)三角形不等式:(,)(,)(,)f x y f x z f z y ≤+对任意的实数z 均成立.今给出四个二元函数:①(,)||f x y x y =-;②2(,)()f x y x y =-③(,)f x y =;④(,)sin()f x y x y =-.则能够成为关于的x 、y 的广义“距离”的函数的所有序号是 .三、解答题:本大题共6小题,共74分,解答时应写出必要的文字说明、证明过程或演算步骤.17.(本小题满分12分)已知函数2()2sin cos f x x x x ωωω=+0ω>)的最小正周期为π. (Ⅰ)求函数)(x f 的单调增区间; (Ⅱ)将函数)(x f 的图象向左平移6π个单位,再向上平移1个单位,得到函数()y g x =的图象.若()y g x =在[0,](0)b b >上至少含有10个零点,求b 的最小值.18.(本小题满分12分)已知数列{}n d 满足n d n =,等比数列{}n a 为递增数列,且251021,2()5n n n a a a a a ++=+=,N n *∈.(Ⅰ)求n a ;(Ⅱ)令1(1)n n n c a =--,不等式2014(1100,N )k c k k *≥≤≤∈的解集为M ,求所有()k k d a k M +∈的和.19.(本小题满分12分)在ABC ∆中,角A B C 、、对边分别是a b c 、、,且满足222()AB AC a b c ⋅=-+ .(Ⅰ)求角A 的大小;(Ⅱ)若a =ABC ∆的面积为,b c .20.(本小题满分12分)已知函数2()2(R)f x x x b b =++∈.(Ⅰ)若函数()f x 的值域为[0,)+∞,若关于x 的不等式()(0)f x c c <>的解集为(,6)(R)k k k +∈,求c 的值;(Ⅱ)当0b =时,m 为常数,且01m <<,11m t m -≤≤+,求2()()21f t t t f t t ---+的取值范围.21.(本小题满分13分)某连锁分店销售某种商品,每件商品的成本为4元,并且每件商品需向总店交(13)a a ≤≤元的管理费,预计当每件商品的售价为(79)x x ≤≤元时,一年的销售量为2(10)x -万件.(Ⅰ)求该连锁分店一年的利润L (万元)与每件商品的售价x 的函数关系式()L x ; (Ⅱ)当每件商品的售价为多少元时,该连锁分店一年的利润L 最大,并求出L 的最大值. 22.(本小题满分13分)已知函数21()2xf x e x ax =--(R)a ∈. (Ⅰ)若函数()f x 的图象在0x =处的切线方程为2y x b =+,求a ,b 的值; (Ⅱ)若函数在R 上是增函数,求实数a 的取值范围;(Ⅲ)如果函数21()()()2g x f x a x =--有两个不同的极值点12,x x ,证明:a >高三数学(理科)练习题 参考答案及评分标准一、选择题:本大题共12小题.每小题5分,共60分. B A D A C D A C B C A D二、填空题:本大题共4小题,每小题4分,共16分.13.2- 14. 23π15.1- 16.① 三、解答题:本大题共6小题,共74分,解答时应写出必要的文字说明、证明过程或演算步骤. 17.(本小题满分12分) 解:(Ⅰ)由题意得()f x =22sin cos x x x ωωω+sin 222sin(2)3x x x πωωω=-=- ………………2分由周期为π,得1ω=. 得()2sin(2)3f x x π=- ………………4分由正弦函数的单调增区间得222232k x k πππππ-≤-≤+,得5,1212k x k k Z ππππ-≤≤+∈ 所以函数)(x f 的单调增区间是5[,],Z 1212k k k ππππ-+∈ ………………6分 (Ⅱ)将函数)(x f 的图象向左平移6π个单位,再向上平移1个单位, 得到2sin 21y x =+的图象,所以()2sin 21g x x =+…………………………8分 令()0g x =,得:712x k ππ=+或11(Z)12x k k ππ=+∈…………………………10分 所以在每个周期上恰好有两个零点,若()y g x =在[0,]b 上有10个零点, 则b 不小于第10个零点的横坐标即可, 即b 的最小值为115941212πππ+= …………………………12分18.(本小题满分12分)解:(Ⅰ)设{}n a 的首项为1a ,公比为q ,所以42911()a q a q =,解得1a q = …………2分 又因为212()5n n n a a a +++=,所以22()5n n n a a q a q += 则22(1)5q q +=,22520q q -+=,解得12q =(舍)或2q = …………4分 所以1222n n n a -=⨯= …………6分 (Ⅱ)则1(1)1(2)n n n n c a =--=--, n d n =当n 为偶数,122014n n c =-≥,即22013n≤-,不成立当n 为奇数,1+22014n n c =≥,即22013n≥,因为10112=10242=2048,,所以21,549n m m =+≤≤ …………9分 则{}k d 组成首项为11,公差为2的等差数列{}()k a k M ∈组成首项为112,公比为4的等比数列则所有()k k d a k M +∈的和为114510110145(11+99)2(14)2204825377247521433--++=+=-…………12分 19.(本小题满分12分) 解:(Ⅰ)由题意可得2222cos 2bc A a b c bc =---, ………………2分由余弦定理2222cos a b c bc A =+-得4cos 2bc A bc =-, ……………4分∴1cos 2A =-, ∵0A π<<,∴23A π= ………………6分(Ⅱ)1sin 162S bc A bc ==⇔= ………………8分222222c o s 328a b c b c A b c b c =+-⇔+=⇔+=………………10分解得:4b c == ………………12分20.(本小题满分12分)解(Ⅰ)由值域为[0)+∞,,当22=0x x b ++时有440b =-=V , 即1b = …………2分则22()21(1)f x x x x =++=+,由已知2()(1)f x x c =+<解得1x +<11x < ……………4分不等式()f x c <的解集为(6)k k +,,∴1)(1)6-==, 解得9c = ……………6分(Ⅱ)当0b =时,2()2f x x x =+,所以22()=()211f t t t t f t t t ---++因为01m <<,11m t m -≤≤+,所以0112m t m <-≤≤+<令2()=1t g t t +,则2221()=(1)t g t t -'+……………8分当01t <<时,()0g t '>,()g t 单调增,当12t <<时,()0g t '<,()g t 单调减, 所以当1t =时,()g t 取最大值,1(1)2g =……………10分 因为2211(1)(1)(1)1(1)1m mg m g m m m -+--+=--+++ 32220[(1)1][(1)1]m m m -=<-+++,所以(1)(1)g m g m -<+ 所以2()=1t g t t +的范围为211[,](1)12m m --+……………12分 21.(本小题满分13分)解: (Ⅰ)由题得该连锁分店一年的利润L (万元)与售价x 的函数关系式为2()(4)(10),[7,9]L x x a x x =---∈. ……………………………3分(Ⅱ)2()(10)2(4)(10)L x x x a x '=-----(10)(1823),x a x =-+- …………………………………………6分 令'()0L x =,得263x a =+或10x = ……………………………8分 20213,6833a a ≤≤∴≤+≤ . ①当2673a +≤,即312a ≤≤时,[7,9]x ∴∈时,()0L x '≤,()L x 在[7,9]x ∈上单调递减,故max ()(7)279L x L a ==- ……………10分②当2673a +>,即332a <≤时,2[7,6]3x a ∴∈+时,'()0L x >;2[6,9]3x a ∈+时,()0L x '<()L x ∴在2[7,6]3x a ∈+上单调递增;在2[6,9]3x a ∈+上单调递减,故3max 2()(6)4(2)33a L x L a =+=- ……………12分答:当312a ≤≤每件商品的售价为7元时,该连锁分店一年的利润L 最大,最大值为279a -万元;当332a <≤每件商品的售价为263a +元时,该连锁分店一年的利润L 最大,最大值为34(2)3a-万元. ……………13分22.(本小题满分13分) 解:(Ⅰ)∵()x f x e x a '=--,∴ (0)1f a '=-.于是由题知12a -=,解得1a =-.………………………………………………2分 ∴ 21()2xf x e x x =-+. ∴ (0)1f =,于是120b =⨯+,解得1b =.……………………………………………………4分(Ⅱ)由题意()0f x '>即0xe x a --≥恒成立,∴ xa e x ≤-恒成立.……………………………………………………5分 设()xh x e x =-,则()1xh x e '=-.当x 变化时,()h x '、()h x 的变化情况如下表:∴min()h x ,∴1a ≤…………………………………………………………………………8分 (Ⅲ)由已知222211()22xx g x e x ax ax x e ax ax =---+=--, ∴ ()2x g x e ax a '=--.∵12 ,x x 是函数()g x 的两个不同极值点(不妨设12x x <), ∴20xe ax a --=(*)有两个不同的实数根12 ,x x ………………………10分当12x =-时,方程(*)不成立 则21x e a x =+,令()21x e p x x =+,则2(21)()(21)x e x p x x -'=+ 由()0p x '=得:12x =当x 变化时,()p x ,()p x '变化情况如下表:x1(,)2-∞- 11(,)22- 12 1(,)2+∞ ()p x - - 0 + ()p x ' 单调递减 单调递减 极小值 单调递增 ∴当1(,)2x ∈-∞-时,方程(*)至多有一解,不合题意;……………12分当1(,)2x ∈-+∞时,方程(*)若有两个解,则1()22a p >=所以,a >13分。
山东省青岛开发区一中2014届高三12月月考物理Word版含答案

物 理2013.12本试眷分第I 卷和第II 卷两部分,共6页,满分100分,考试时间90分钟。
答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号填写在答题卡上规定的位置。
考试结束后,将答题卡交回。
注意事项:1.第I 卷共12小题,每小题选出答案后,须用2B 铅笔把答题卡上对应题号的答案标号涂黑,如需改动,越须先用橡皮擦干净后,再改涂其他答案标号。
只能涂在答题卡上,答在试卷上无效.2.第Ⅱ共6小题,所有题目的答案,考生须用0.5毫米的黑色签字笔答在答题卡上各题目指定的区域内,在试卷上答题无效;作图时先用铅笔作出正确图形,然后再用黑色签字笔描黑;如需改动,先划掉原来的答案,然后再写上新的答案.第I 卷(选择题 共36分)一、本题包括12小题,每小题3分,共36分。
在每小题给出的四个选项中,至少有一 个选项是正确的。
全部选对的得3分,选对但不全的得2分,选错或不答的得0分。
l. 以下叙述正确的是A.牛顿发现了万有引力定律并测得了引力常量B.元电荷P 的数值最早是密立根通过实验测得的C.奥斯特在实验中观察到电流的磁效应,该效应解释了电和磁之间存在联系D.安培根据通电螺线管的磁场和条形磁铁的磁场的相似性,提出了分子电流假说 2如图所示,直线a 和曲线b 分别是在平直公路上行驶的汽车a 和b 的位置一时间(x-t 图线。
由图可知A.在时刻1t ,a 车从后面追上b 车B .在时刻2t ,a 、b 两车运动方向相反C .在1t 到2t 这段时间内,b 车的速率先增加后减少D. 在1t 到2t 这段时间内,b 车的速率一直比a 车的大3.L 型木板P (上表面光滑)放在固定斜面上,轻质弹簧一端固定在木板上,另一端与置于木板上表面的滑块Q 相连,如图所示。
若P 、Q-起沿斜面匀速下滑,不计空气阻力。
则木板P 的受力个数为A. 3B. 4C .5 D. 64 1970年4月24日,我国自行设计、制造的第一颗人造地球卫星“东方红一号”发射成功,开创了我国航天事业的新纪元。
山东省青岛开发区一中高三生物12月月考(扫描版)新人教

山东省青岛开发区一中2014届高三生物12月月考(扫描版)新人教
版
参考答案
一、选择题:1~20题每题1分,21~40题每题2分,共60分。
二、非选择题:共40分。
41.每空1分,共8分。
(1)有核膜① (2)胞吐主动运输或协助扩散
(3)减少分散转移(4)氨基酸基因
42.每空1分,共7分。
(1)碱性染料(2)② 二
(3)联会非姐妹染色单体(4)①④ ⑤
43.每空1分,共7分。
(1)淋巴因子抗体(2)吞噬细胞增殖、分化
(3)②③④(4)增加神经—体液调节
44.每空1分,共8分。
(1)内膜向内突出形成嵴类囊体薄膜
(2)②③
(3)O2 减少
(4)CO2浓度暗反应增强增加
45.除注明外,每空1分,共10分。
(1)AABB AAbb
(2)7 有色羽毛∶白色羽毛=8∶1
(3)AABB、AABb、AAbb
(4)①aabb
③全为有色(2分)出现有色、白色两种性状(2分)
11。
山东省青岛开发区一中2013届高三12月月考试题 地理 含答案

山东省青岛开发区一中2013届高三12月月考试题地理试题本试卷分第I卷(选择题)和第II卷(菲选择题)两部分。
全卷共10页.共100分。
考试时间90分钟.注意事项:1. 答卷前,考生务必将自己的姓名、考号填写在第II卷上.2. 选择题每小题选出答案后,用2B铅笔将答题卡上对应题目答案标号涂黑,如需改动,用橡皮擦干净后,再涂其它答案标号.标在试题卷上无效。
3。
非选择题用0。
5毫米的黑色墨水签字笔.4。
考试结束后,请将第II卷上交第I卷、选择题(60分)图5为某国人口增长和城市人口比重统计图,读图回答1、2题。
1。
该国城市化进程最快的时段是A.l967 - 2008 年B。
1915 —1967 年C. 1776 —1915 年D。
1776 年以前2。
图6中,能正确反映该国城市人口分布的是下图是城市形成与发展区位示意图,图中a、b、c表示城市发展过程。
读图回答3—4题。
3.下列城市中,与城市发展过程相吻合是 ( )A.a—武汉 B.b—昆明 C.b—香港 D.c—克拉玛依4.以a过程形成的大城市,可持续发展的措施中,可行的是 ( ) A.积极发展第一产业B.进行产业转移C.控制人口增长数量D.积极发展第三产业,促进经济结构多元化5.关于田纳西河的叙述,正确的是A。
位于美国中部,发源于西部高山B。
是密西西比河上有一条流程最长、水量最大的支流C。
流域为亚热带气候,冬末春初多雨D.水系发达、支流众多,是美国通航里程最长的河流水库具有多种功能,如防洪、发电等,并且能改善局部地区的气候。
图10是某水库洪水时径流调节示意图。
读图回答6、7题.6。
图中水库最高水位出现的时间是A。
t1 B. t2 C t1与t2之间D。
t3—t4之间7. 下列叙述中,能正确反映该地区在水库蓄水后各地理要素变化的是A. 气温日变化大幅增加B。
夏季时,库区易形成对流运动,降水量增加C. 下游洪峰出现时间滞后。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理科数学 2013.12本试卷分第I 卷和第Ⅱ卷两部分,共4页。
满分150分。
考试时间120分钟。
考试结束后,将本试卷和答题卡—并交回。
注意事项:1.答题前,考生务必用0.5毫米黑色签字笔将姓名、座号、考生号、县区和科类填写在答题卡和试卷规定的位置上。
2.第I 卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
3.第II 卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、 修正带。
不按以上要求作答的答案无效。
4.填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤。
参考公式:S 是锥体的底面积,,h 是锥体的高。
R 是球的半径。
第I 卷(共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1),则A B =(A){}|12x x << (B){}|12x x -<< (D){}|11x x -<< (2)若函数21,1()ln ,1x x f x x x ⎧+≤=⎨>⎩则(())f e (e 为自然对数的底数)=(A)0 (B)1 (C)2 (D)2ln(1)e +(3)已知α为第二象限角,且,则tan()πα+的值是(4)则“函数()x f x a =”在R 上是增函数”是“函数()ag x x =”“在(0,)+∞上是增函数”的(A)充分不必要条件 (B)必要不充分条件(C)充要条件 (D)既不充分也不必要条件(5)(6)(7)的图象向右平移(0)m m >个单位长度后,所得到的图象关于 y m(8)设数列{}n a 是由正数组成的等比数列,n S 为其前n 项和,已知2431,7a a S == ,则5S =(A)(9)已知,,a b c R ∈,给出下列命题:①若a b >,则22ac bc >;②若ab ≠0,③若0,a b n N *>>∈,则n n a b >; ④若log 0(0,1)a b a a <>≠,则a ,b 中至少有一个大于1.其中真命题的个数为 (A)2 (B)3 (C)4 (D)1 (10)已知某几何体的三视图如右图所示,其中,主(正)视图, 左(侧)视图均是由直角三角形与半圆构成,俯视图由圆 与内接直角三角形构成,根据图中的数据可得此几何体的体积为( )(B)(C)(A) (B) (C) (D)(11)若ABC ∆外接圆的半径为1,圆心为O .且,则CA CB 等于(D)3 (12)设函数[)()1,,1,f x n x n n n N =-∈+∈,则方程2()log f x x =的根有(A)1个 (B) 2个 (C)3个 (D)无数个第II 卷(共90分)二、填空题:本大题共4小题,每小题4分,共16分.(13)已知向量(1,2)a =,向量(,2)b x -,且()a a b ⊥-,则实数x 等于______________.. ,若目标函数(0,0)z abx y a b =+>> 的最大值为8,则a+b 的最小值为_____________.(16)若二次函数2()(0)f x ax bx c a =++≠的图象和直线y=x 无交点,现有下列结论: ①方程[()]f f x x =一定没有实数根;②若a>0,则不等式[()]f f x x >对一切实数x 都成立; ③若a<0,则必存在实数0x ,使00[()]f f x x >;④函数2()(0)g x ax bx c a =-+≠的图象与直线y=-x 一定没有交点,其中正确的结论是____________(写出所有正确结论的编号). 三、解答题:本大题共6小题,共74分. (17)(本小题满分12分)在ABC ∆中,角A 、B 、C 的对边分别为a 、b 、c ,且角A 、B 、C 成等差教列. ( I)c 的值; ( II)设sin sin t A C =,求f 的最大值. (18)(本小题满分12分)已知函数()22,xxf x k k R -=+∈ . ( I)若函数()f x 为奇函数,求实数k 的值;( II)若对任意的[)0,x ∈+∞,都有()2xf x ->成立,求实数k 的取值范围.(19)(本小题满分12分)在四棱锥P-ABCD 中,侧面PCD ⊥底面ABCD ,PD ⊥CD ,底面ABCD 是直角梯形,AB ∥DC ,90,1,2ADC AB AD PD CD ∠===== ADC -900,AB= AD= PD=1.CD=2.(I)求证:BC ⊥平面PBD :(II)设E 为侧棱PC 上异于端点的一点,PE PC λ=,试确定λ的值,使得二面角E-BD -P 的大小为45 .(20)(本小题满分12分)已知等差数列{}n a 满足:11(),1n n a a n N a *+>∈=,该数列的前三项分别加上l ,l ,3后顺次成为等比数列{}n b 的前三项. (I)求数列{}n a ,{}n b 的通项公式; ( II)求c 的最小值.(21)(本小题满分13分)某建筑公司要在一块宽大的矩形地面(如图所示)上进 行开发建设,阴影部分为一公共设施不能建设开发,且要求 用栏栅隔开(栏栅要求在直线上),公共设施边界为曲线 2()1(0)f x ax a =->的一部分,栏栅与矩形区域的边界交于点M 、N ,切曲线于点P ,设(,())P t f t .( I)将OMN ∆(O 为坐标原点)的面积S 表示成f 的函数S(t); (II)S(t)取得最小值,求此时a 的值及S(t)的最小值.(22)(本小题满分13分)已知函数()ln r x x =,函数 ( I)试求f (x)的单调区间。
(II)若f (x)在区间[)1,+∞上是单调递增函数,试求实数a 的取值范围:(ⅡI)设数列{}n a 是公差为1.首项为l n 项和为n S ,求证:当1a =时,参考答案一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1-5 BCDAC 6-10ADBAC 11-12DC二、填空题:本大题共4小题,每小题4分,共16分.(13)9;(14;(15)4; (16)①②④ 三、解答题:本大题共6小题,共74分.(17)解:(Ⅰ)因为角A B C 、、成等差数列,所以2B A C =+,因为A B C ++=π,所以………2分 ,3a =,2222cos b a c ac B =+-, 所以2340c c --=.所以4c =或1c =-(舍去). …………6分………………9分……………12分(18)解:(Ⅰ)因为()22x x f x k -=+ 是奇函数,所以()(),R f x f x x -=-∈, ………2分即22(22),x x x x k k --+=-+ 所以2(1)(1)20x k k +++= 对一切R x ∈恒成立, 所以1k =-. ……………6分(Ⅱ)因为[)0,x ∈+∞,均有()2,x f x ->即222x x x k --+> 成立,所以212x k -<对0x ≥恒成立, ……………8分所以2min 1(2)x k -<,因为22x y =在[)0,+∞上单调递增,所以2min (2)1x =, 所以0k >. ……………12分(19) (Ⅰ)证明:因为侧面PCD ⊥底面ABCD ,PD ⊥CD ,所以PD⊥底面ABCD ,所以PD ⊥AD .又因为ADC ∠=90 ,即AD ⊥CD ,以D 为原点建立如图所示的空间直角坐标系, 则(1,0,0)A ,(1,1,0)B ,(0,2,0)C ,(0,0,1)P ,所以(1,1,0),(1,1,0).DB BC ==-所以0DB BC ⋅=,所以BC BD ⊥ 由PD ⊥底面ABCD ,可得PD BC ⊥,又因为PD DB D = ,所以BC ⊥平面PBD . ……5分 (Ⅱ)由(Ⅰ)知平面PBD 的一个法向量为(1,1,0)BC =- ,且(0,0,1)P ,(0,2,0)C ,所以(0,2,1)PC =- ,又PE PC = λ,所以(0,2,1)E -λλ,(0,2,1)DE =-λλ. (7)分设平面EBD 的法向量为(,,)a b c =n ,因为(1,1,0)DB =,由0DB = n ,0DE =n ,得02(1)0a b b c +=⎧⎨+-=⎩λλ,令1a =-,则可得平面EBD 的一个法向量为……………10分又由题意知()0,1∈λ,故 ……………12分 (20) 解: (Ⅰ)设d q 、分别为数列{}n a 的公差、数列{}n b 的公比.由题意知,11a =,231,12a d a d =+=+,分别加上1,1,3得2,2,2d d ++4,2(2)2(42),2d d d +=+=±所以又1n n a a +>,所以0d >,所以2d =,所以21n a n =-(*n ∈N ),由此可得12b =24b =,2q =,所以2n n b =(*n ∈N ). ……………6分……………10分分(21)解:(Ⅰ)2y ax '=-,直线MN 的斜率为2at -,∴直线MN的方程为2(1)2()y at at x t --=--令0,y = (3)分令0x =,得2222121,(0,1)y at at at N at =-+=+∴+,MON ∴∆的面积 (6)分因为0,0a t >>,由()0S t '=, ………9分 , ()0S t '>, ,, ()S t 取得最小值,………13分(22)解:(Ⅰ)()f x =因为0a >,0x >,所以20ax >,令10ax ->, 所以()f x 的单调递增区间是;()f x 的单调递减区间是 (4)分(Ⅱ)若()f x 在[1,)x ∈+∞是单调递增函数,则'()0f x ≥恒成立,即因为[1,)x ∈+∞,…………….7分令1,2,,1,(x n n *=-∈ N 且2)n ≥时, 将所得各不等式相加,得……………13分。
