振荡电偶极子的辐射资料
电偶极子振荡产生的电磁辐射

电偶极子振荡产生的电磁辐射摘要随着电子信息时代的高速发展,信息传递要求我们更加高效,在我们生活的三维时空里速度最大值为光速,而以人为力量要想到达此速度几乎不可能,但是我们知道电磁波的传播速度为光速(真空),我们可以利用将信息加载在电磁波上传递来达到高效传输。
因此我们如今大多采用电磁波传递信息。
电偶极子辐射是电磁波辐射理论的基础,清楚地了解它的辐射规律是非常重要的,在辐射问题的实际应用中,可以计算辐射功率和辐射的方向性。
电偶极子辐射的电磁波是空间中的TM 波,TM波在现实中有多方面的应用。
电偶极辐射是天线工程中最基本的问题,电偶极子是电介质理论和原子物理学的重要模型,研究从稳恒到 X光频电磁场作用下电介质的色散和吸收,以及天线的辐射等现象,可以用振荡偶极子。
本文采用微分方程在边界条件下解出电偶极辐射的数学表达式,我们重点研究远场辐射问题。
这对电磁波辐射理论的数学直观化有一定意义,对于我们了解辐射以及辐射的原理有重要意义。
关键字:电偶极辐射微分模型边界问题1问题重述电偶极子(electric dipole)是两个相距很近的等量异号点电荷组成的系统。
电偶极子的特征用电偶极距P=Lq描述,其中 L是两点电荷之间的距离,L和P的方向规定由,q指向+q。
电偶极子在外电场中受力矩作用而旋转,使其电偶极矩转向外电场方向。
电偶极矩就是电偶极子在单位外电场下可能受到的最大力矩,故简称极矩。
如果外电场不均匀,除受力矩外,电偶极子还要受到平移作用。
电偶极子产生的电场是构成它的正、负点电荷产生的电场之和。
当其在水平面上发生振荡是会辐射出电磁波,求解在远区电磁场强度的解析解。
问题分析一对等量异号的电荷组成的带电系统,当它们之间的距离L远比场点到它们的距离r小得多(r>>L)时,我们把这种带电体系叫做电偶极子.当点电偶极子两端的电荷交替变化时,在其附近空间将产生交变电磁场,并使电磁场往远处辐射.通常,交变电偶极子上的电荷变化可视为一个电流元.最简单的辐射电流元是一个很短的直线电流元设此电流元的长度L总是远小于自由空间的电磁波电偶极子波,长.即L<<,则可以认为其上电流的幅值和相位处处相同,即电流均匀分布;且其直径d与其长度相比可忽略不计,即有d<<L,反之,根据电流连续性原理,电流元两端必有等值而异号的电荷积聚,相当于一个交变的电偶极子这样对交变电偶极子的分析也就是对电流元的分析,这种短直线电流元称为电偶极子或基本振子,也称为赫兹振子.赫兹振子的辐射也就叫做电偶极辐射.根据麦克斯韦方程组和在利用2推迟势计算辐射是解决辐射问题的一般思路。
电动力学五三(电偶极辐射)

k /c
波数
4
令
i t Α( x, t ) Α( x)e
' ikr 0 J ( x )e ' ( x ) dV 4 r
有
e
ikr
推迟作用因子 , 表示 电磁波传至场点时有 相位滞后kr。
5
由电荷守恒 定律,在一 定频率的交 变电流情形 中有
8
电荷到场点的距离r
本节研究分布于一个小区 域内的电流所产生的辐射。小 区域是指它的线度远小于波长 以及观察距离r,即
l , l r
9
对于r和的关系,可以区别三种情况
r
近区 感应区
三个区域场的特点是不同的 近区:
e ~1 kr 1 场保持恒定场 电场具有静电场的纵向形式 磁场也和恒定场相似
在辐射问题的实际应用中,最主要的问题 是计算辐射功率和辐射的方向性。这些都可 以由平均能流密度 S 求出。电偶极辐射的平 均能流密度
1 c S Re (Ε Η ) Re [(Β n) Β] 2 2 μ0 2 p 2 c 2 Β n sin θ n 2 3 2 2 μ0 32π ε0c R
24
电偶极辐射角分布: sin2 表示电偶极辐射的 角分布,即辐射的方向 性
电偶极矩横断面
90
辐射最强
没有辐射
25
电偶极矩轴线方向 0,
总辐射功率P
Ρ S R d
2 2 p
i t
32 0 c
2
3
sin d
2
1
2 p 3
' r J(x ,t ) 0 ' c ( x , t ) dV 4 r
电动力学课件 5.3 电偶极辐射
e ikR 0 e ikR 0 B x, t A x, t p t pt 4 R R 4 0 e ikR ike R p t 4 R p t p t i p t 由于 k 0 0 t 1 c p t i p t 2 p t 0 0 e ikR e ikR 1 B x, t p t eR p t sin e 3 3 4 0 c R 4 0c R
§5.3 电偶极辐射
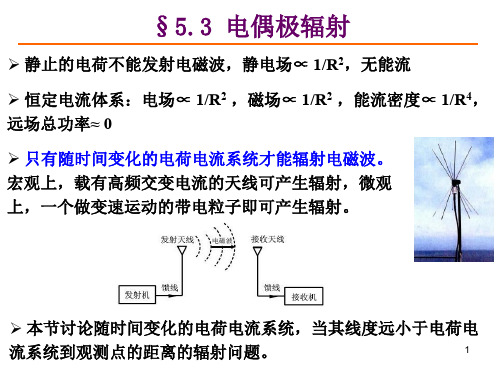
静止的电荷不能发射电磁波,静电场∝ 1/R2,无能流 恒定电流体系:电场∝ 1/R2 ,磁场∝ 1/R2 ,能流密度∝ 1/R4, 远场总功率≈ 0 只有随时间变化的电荷电流系统才能辐射电磁波。 宏观上,载有高频交变电流的天线可产生辐射,微观 上,一个做变速运动的带电粒子即可产生辐射。
电磁场能流密度正比于1/R2,沿径向辐射
e ikR B x, t p t sin e 4 0c 3 R
1
b) 辐射功率 单位时间内通过半径为 R 的球面向外辐射的平均能量,称为 辐射功率。把能流密度 S 对球面积分即得总辐射功率,即
P
S
S ds
dV
任何小区域电荷电流分布在远处某点产生的矢势可表示为位 于原点的各级电磁多极辐射的叠加 3、电偶极辐射
1 1)展开式的第一项 A x 与电偶极矩 p t 的关系
7
ikR e 由于 A1 x 0 J x dV 4 R V ikR ikR e e 1 A x , t 0 J x e i t dV 0 J x , t dV 4 R V 4 R V
5-3 电偶极辐射解析

从而得到矢势A的展开式为:
0 eikR 1 2 A( x ) J ( x ) 1 ik n x ( ik n x ) 4 R V 2!
展开式的各项对应于各级电磁多极辐射。
三、电偶极辐射
展开式的第一项
ikR e A(1) ( x ) 0 4 R
在近区内, kr <<1 ,推迟因子 eikr~1 ,因而场保持
稳恒场的主要特点,即电场具有静电场的纵向形式,
磁场也和稳恒场相似。 b) 远区(辐射区)r>>λ,而且也保证r>>l。
1 1 在此区域中场强E和B均可略去 的高次项, R | x |
该区域内的场主要是横向电磁场。
c) 感应区(过渡区),r ~ λ,但满足r>>l。 这个区域是一个过渡区域。它介于似稳区和辐射区
根据小区域的意义
l ~| x | ,
l ~| x | r.
因此,在计算辐射场时只须保留1/R的最低次项。 而 R r , r | x |,所以分母中可以去掉 n x 项。但分子不能去掉 n x 项,这是因为这项贡献 一个相因子: ikn x i 2n x /
若电流 J ( x, t ) 是一定频率ω的交变电流,有
J ( x, t ) J ( x)e
因此
it
式中 k c 为波数
0 J ( x)ei ( k r t ) Α( x, t ) dV 4 r
如果令 A( x, t ) A( x )e it
( x, t )
40 r
c dV
由此可见,由矢势公式就可以完全确定电磁场。 磁场
ic 电场(在电荷分布区域外面) Ε Β k 二、矢势A的展开式
振荡偶极子的辐射公式推导

振荡偶极子的辐射公式推导好啦,今天咱们来聊聊一个特别酷的物理话题——振荡偶极子的辐射公式。
这名字听起来是不是有点高大上?别担心,接下来我会带着你一起轻松走一遍,保证让你听完之后点个赞,心里一阵豁然开朗!说到振荡偶极子,你就可以想象成一个电荷在不停地“跳舞”,它既不乖乖站着,也不完全离开舞池,它在上蹿下跳,发出一阵又一阵的能量,向外辐射。
你可能会问,电荷怎么可能跳舞?嗯,别忘了,在物理的世界里,什么都有可能。
好了,我们从头开始。
假设你有一个电荷,这个电荷并不是一成不变的静止在那里,而是在两点之间做振荡。
你可以把它想象成在一个“电场”中的舞者,不断地来回摆动。
那时候,电荷的速度和位置都在不停变化,而这些变化最终会影响它周围的电场和磁场。
对了,记得刚刚说的那种“跳舞”的状态,就是我们常说的振荡。
电荷振荡的频率决定了它会以什么样的模式发出电磁波。
这里的“频率”可不是咱们耳朵能听到的音乐,而是电荷每秒钟摆动的次数。
有些人可能想,这样的电荷会有什么影响?好嘛,影响大了去了!振荡的电荷会发出电磁波,这些电磁波就像是我们生活中常见的光波一样,只不过频率可能低得多,甚至在人眼无法察觉的范围内。
这些电磁波不仅能影响周围的物体,还能传播到远方,带走能量。
想想看,如果你在湖面上扔个石子,水面上的波纹就会扩散开来,离得越远波纹的幅度就越小。
振荡偶极子就是这么给外界“丢”出一圈又一圈的波纹。
至于这个“偶极子”,那可是有点学问的。
偶极子一般指的是两种相反电荷靠得很近,比如一个正电荷和一个负电荷。
你可以想象成正负电荷在一起搞对抗,谁也不让谁,但它们就像两位相对的演员,总是表演着电场的互动。
一个电荷在振荡时,它们之间的电场会发生变化,周围的空间也因此发生了波动。
振荡的电荷并不是随便发射辐射,而是按规律来的。
这个规律就是有名的辐射公式了。
这公式其实并不复杂,虽然看起来好像很科学,但别怕!它主要是通过电荷的加速度来描述辐射。
想一想,当电荷加速时,就像是跑步时加速一样,释放出来的能量就更多。
电偶极辐射_38p

两个金属球相距很近,充电到很高的电压,使周围空气击穿 而放电,就形成一个振荡的电偶极子. 本节研究宏观电荷系统在其线度远小于波长情形下的远区辐 射问题。即讨论电荷分布以一定频率做周期运动,且电荷体 系线度远远小于电荷到观测点的距离的情况。
具体的计算研究思路就是由源的变化出发,确定出势的变化
规律,再算出场量,并且给予充分的讨论。
曲面上的矢径长表示 E 的数 值对 q 和 j 的函数关系。 曲面上的曲线,是 j 为常数 的曲线,每隔10 度画一条。
为清楚起见,曲面切成了两
半。
沿着y轴的方向,两个波相加,合成的电场强度是单个天线所产生 的两倍。沿着x轴,两个波相位相反而互相抵消了。在xz平面的其 他方向上,波并不完全抵消,因为路程差比l/2小。每个天线在z轴
t
r A( xv)
=
µ0
r J
(
xr′)eikr
dV
′
4π r
(2) 辐射场电荷密度
∂ρ(xv,t) = −∇ ⋅ Jv(xv,t) = −[∇ ⋅ Jv(xr)]exp(− iωt) ∂t
ρ(xv,t)
=
1
iω
∇
⋅
Jv(xv,t)
令 ρ ( xr, t) = ρ ( xr)e−iω t
5-3 电偶极辐射
与R相比,不能略去相因子中 nr ⋅ xr′ 项。
2π nr 5-3亦电即偶极辐射λ
⋅
xr′
相对
2π不一定是小量
20
§5-3-3 偶极辐射
电磁波是从变化电荷电流系统辐射出来的。
在宏观情形,电磁波由载有交变电流的天线辐射出来;
在微观情形,变速运动的带电粒子导致电磁波的辐射。
下面研究宏观电荷电流系统基本辐射元 电偶极子和磁偶极子的辐射问题。 电偶极子的辐射 振荡电偶极子 短直线电流元是最简单、最基本的电磁波辐射源 短直线电流元称为电基本振子, 也叫基元天线 直线电流元的辐射特性是研究更复杂
偶极子天线的辐射

偶极子天线的辐射一、偶极子天线(元天线)1、结构:长为Δl的载流导线,中心馈电⑪本质上是一个LC振荡电路,振荡频率:,⑫为了有效地辐射能量:f↑,L、C↓图9-2-1⑬闭合电路→开放电路→振荡偶极子点击看图2、电特性⑪Δl<<λ,Δl上各点的电流(包括相位)可以看作是相等的,⑫Δl<<r,Δl上各点到P点的距离,可以看作是相等的3、实际的线状天线可看成是许多偶极子天线的串联组合。
二、偶极子天线的辐射1、辐射场表达式⑪设偶极子天线上的电流为,在空间产生的矢量位(达朗贝尔方程的解)在球坐标系中,如图9-2-1⑫由⑬由2、讨论⑪若kr1<<(k<<1/r,r<<λ/2π=,天线近区④~⑥式中,⑨、⑩式是电偶极子产生的电场,p25(2.4.7)式。
电流元产生的磁场与⑧比较,所以⑧式是电流元产生的磁场。
∴①近区的磁场是偶极子上的瞬时电流元产生的,与恒定磁场分布相似,近区的电场是偶极子上的瞬时偶极子产生的,与静电场分布相似。
② E与H相位相差π/2③主要是由于在(4)~(6)→(8)~(10)的过程中,略去了一些小项,实际上是能量交换(电场~磁场)>>传输的能量。
⑫若kr>>1(k>>1/r,r>>λ/2π),天线远区由(4)~(7)式①场强ⅰ)只有, 分量,TEM波。
ⅱ)E、H同频率,同相位。
ⅲ)r相等的各点相位相等――球面波。
②波阻抗自由空间η=120π≈=377Ω。
③3、辐射特性(远区)⑪辐射方向性由远区场强表达式(11)、(12)表明辐射具有一定的方向性:在天线所在的平面内,∝sinθ,θ=0,场强为0;θ=π/2,场强最大;在垂直于天线的平面内无方向性。
①方向图函数ⅰ)定义:ⅱ)偶极子天线,由(12)式 f(θ)=sinθ (15)②方向图:ⅰ)定义:按方向图函数f(θ,φ)绘出的图形称为方向图。
ⅱ)偶极子天线的方向图。
(a)三维方向图(点击链接)(b) 侧视图图9-2-3 (c) 俯视图方向图直观地表示出天线在不同方向上,相同距离处辐射场强的相对大小。
5-3 电偶极辐射

2 it
从而得到: |2 p 2 4 | p 0
P 1 4
0
p0
2
4
3c
3
五、短天线的辐射 辐射电阻 当天线的长度远小于辐 射波长时,它的辐射就 是电偶极辐射。 馈电点处电流有最大值 I0,在天线两段电流为 零。若天线长度l<<,
2
3
பைடு நூலகம்
sin d
S
2 | | p
32 0 c
2 2 | | p 2
3
2
0
d sin d
3 0
32 0 c
3
2
4 3
1 40
2 | | p
3c
3
如果偶极子作简谐振动,角频率为ω ,且有 it p( x, t ) p0 ( x )e 则 ip ip0 ( x )e it p
2n x 一般是不能忽略的,因此
x 要保留,
所以,
A( x )
0
4
V
)eik ( R n x ) J(x R
dV
把相因子对 kn x 展开,得
e
ikn x
1 ikn x
1 2!
) 2 (ikn x
从而得到矢势A的展开式为:
2 x 2n x r R 1 2 R R 1 2
2
z
r
l o x
x
P y
x
, J
由二项式展开得到(略去 x 2 / R 2 等高次项): r R n x 由此得到
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例 证明圆形平板电容器充电时每单位时间內从侧面输 入的电磁能正好等于所储能量随时间的增加率。 解:单位时间输入的电磁能
dD 2 dE Id S 0 r dt dt H 2πr I d
P E H dS
H
Id r
H d
Id r dE H 0 2 πr 2 dt
2
传播方向
总辐射功率:p
球面
Sr sin d d
2
z
r S
4 p0 2 p 3 12π 0 c
章 静电场 第17第 章11 电磁波
库仑定律 17-3 11-2 振荡电偶极子的辐射
17.3.2 赫兹实验
铜棒
A
C
C B
感应线圈
章 静电场 第17第 章11 电磁波
D
库仑定律 17-3 11-2 振荡电偶极子的辐射
章 静电场 第17第 章11 电磁波
库仑定律 17-3 11-2 振荡电偶极子的辐射
r dE P 2 πrd 0 E 2 dt dE πr d 0 E dt
2
H
电容器静电能量:
1 2 2 We 0 E πr d 2
Id r
H d
dWe dE 2 增加率: P πr d 0 E dt dt
振荡电偶极子附近的电磁场线
p p0 cos t
B
c
c
+ -
+ + + +
E
E
B
c
章 静电场 第17第 章11 电磁波
c
库仑定律 17-3 11-2 振荡电偶极子的辐射 极轴 p0 sin r E cos (t ) E 2 4π 0c r c 2 p0 sin r H cos (t ) H r 4π 0cr c p0 4 2 2 p0 sin r 2 S EH cos (t ) 2 3 2 16π 0c r c
库仑定律 17-3 11-2 振荡电偶极子的辐射
17.3.1 电磁波的产生
变化的电磁场在空间以一定的速度传播就形成 电磁波
T 2 π LC
+ Q
+
L
C
Q0
章 静电场 第17第 章11 电磁波
振荡电偶极子
库仑定律 17-3 11-2 振荡电偶极子的辐射
不同时刻振荡电偶 极子附近的电场线
