11光学传递函数
【国家自然科学基金】_波前编码_基金支持热词逐年推荐_【万方软件创新助手】_20140730
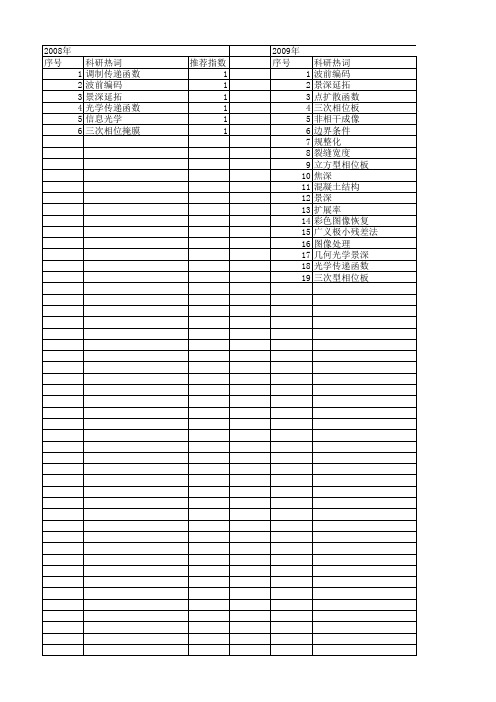
科研热词 调制传递函数 波前编码 景深延拓 光学传递函数 信息光学 三次相位掩膜
推荐指数 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
科研热词 波前编码 景深延拓 点扩散函数 三次相位板 非相干成像 边界条件 规整化 裂缝宽度 立方型相位板 焦深 混凝土结构 景深 扩展率 彩色图像恢复 广义极小残差法 图像处理 几何光学景深 光学传递函数 三次型相位板
推荐指数 6 3 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8
科研热词 波前编码 维纳滤波 立方型相位板 点扩散函数(psf) 小波变换 大景深 图像恢复 图像复原
推荐指数 2 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12
2013年 序号 1 2 3 4 5 6 7 8 9
科研热词 调制传递函数相似度 衍射光学元件 波前编码 多分子追踪 变形光栅 双螺旋点扩散函数 动态数据交换 光学设计 优化
推荐指数 1 1 1 1 1 Байду номын сангаас 1 1 1
2011年 科研热词 面形检测 零位补偿 自适应光学 波前编码 景深扩大 对数位相掩膜板 复用计算全息元件 光学设计 偏置模式波前传感器 传感器 三次位相板 zernike像差模式 推荐指数 1 1 1 1 1 1 1 1 1 1 1 1
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
科研热词 推荐指数 波前编码 2 三次相位板 2 面型参数设计 1 计算全息图 1 自由曲面 1 离焦极限 1 湍流大气 1 波前畸变 1 反镜像边界条件 1 双共轭梯度平方稳定算法 1 光无线通信 1 光学检测 1 wavefront coding 1 design of phase plate 1 defocus limit 1 cubic phase plate 1
【国家自然科学基金】_三线阵ccd_基金支持热词逐年推荐_【万方软件创新助手】_20140802
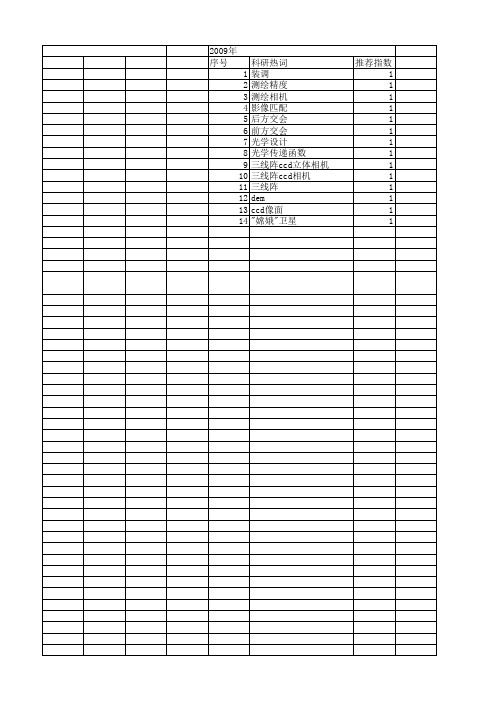
科研热词 装调 测绘精度 测绘相机 影像匹配 后方交会 前方交会 光学设计 光学传递函数 三线阵ccd立体相机 三线阵ccd相机 三线阵 dem ccd像面 "嫦娥"卫星
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1
科研热词 推荐指数 自检校光束法区域网平差 2 空间前方交会 2 ads40 2 资源三号测绘卫星 1 虚拟ccd阵列 1 虚拟ccd线阵 1 系统误差 1 测绘相机 1 模拟成像 1 杂光分析 1 机载线阵ccd传感器 1 机载三线阵ccd影像 1 成像几何模型 1 影像匹配 1 并行算法 1 区域网平差 1 几何标定 1 内视场拼接 1 全色遥感立体测绘图(prism) 1 先进陆地观测卫星(alos) 1 任务调度 1 三线阵 1 ccd影像 1
2010年 序号 1 2 3 4 5 6 7 8 9
科研热词 高斯合地形地貌梯度 区域网平差 仿真系统 三线阵ccd
推荐指数 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13
2014年 序号 1 2 3 4 5
科研热词 附加参数模型 资源三号卫星 自检校 系统误差 光束法区域网平差
推荐指数 1 1 1 1 1
科研热词 自动提取 特征分析 激光高度计 月表轮廓特征 月表形貌 月海与月球高地 数据不一致性 影像匹配 平差控制约束 嫦娥一号 反投影 ce-1三线阵立体相机 ccd影像
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
《傅里叶光学》复习题

《傅里叶光学》复习题----B。
Max。
Feynman一、选择题1、《信息光学》即《傅里叶光学》课程采用的主要数学分析手段是________________。
A、光线的光路计算B、光的电磁场理论C、空间函数的付里叶变换222、高斯函数的付里叶变换为________________。
exp[,,(x,y)]22A、1 B、,(f,f) C、 exp[,,(f,f)]xyxy3、1的付里叶变换为_________________。
,(f,f)Comb(f)Comb(f)A、 B、 C、 sgn(x)sgn(y)xyxy4、余弦函数的付里叶变换为_________________。
cos2,fx01sin(f)sin(f)A、 B、 C、1 [,(f,f),,(f,f)]xyx0x025、圆函数Circ(r)的付里叶变换为_________________,,J(2)1,(f,f)A、 B、1 C、 xy,6、在付里叶光学中,通常是以_________________理论为基础去分析各种光学问题的。
A、非线性系统B、线性系统7、_________________是从空间域内描述相干光学系统传递特性的重要光学参量。
A、脉冲响应B、相干传递函数8、_________________是从空间频域内描述相干光学系统传递特性的重要光学参量。
A、脉冲响应B、相干传递函数9、_________________是从空间域内描述非相干光学系统传递特性的重要光学参量。
A、点扩散函数B、非相干传递函数(光学传递函数)10、_______________是从空间频域内描述非相干光学系统传递特性的重要光学参量。
A、点扩散函数B、非相干传递函数(光学传递函数)U,Aexp[i2,(fx,fy)]11、某平面波的复振幅分布为那么其在不同方向(x,y)xy 的空间频率为_________________,它也是复振幅分布的空间频谱。
计算机辅助光学设计codeV

第二章 光学自动优化设计 的基本方法
概述 评价函数的概念及其构成 最优化方法 边界条件的控制
光学自动优化设计概述
光学设计的目的 找到一组结构参数(r、d、材料等), 使之满足预定的光学性能,外形尺寸和 成像质量等要求 方法 数学的最优化方法和计算机在光学设 计中的应用
光学自动优化设计概述
A
-U
U'
L' -l l'
-L'
返回
图5.1
T'
球差的影响与危害
一个点形成的像为一个圆斑,破坏了理 想成像的对应关系,使像点变得模糊, 降低了成像的清晰度和分辨率。 球差产生在轴上点(视场中心处),对 整个像面的影响最为明显,必须加以校 正。
球差曲线
h hm 1 0.707
h h hm 1
高斯像面
-K' t a' z' B' t c Y' b Y' z
a z b B
b'
Y' a
弧矢慧差
入瞳
K s ' Yc 'Yz ' Yd 'Yz '
Y' z B' z -K' s B' c B' d
d' z' d z c'
B' s
Y' z c
高斯 像面
Y' z
B
Y' z
图5.4
慧差的危害影响
11变化称为调制传递函数mtf高频部分反映了物体的细节中频部分反映了物体的层次低频部分反映了物体的轮廓光学传递函数的概念将每一视场点的物体分解为所有频率的余弦物体并求出其理想像以理想像的对比度作为参考实际像的对比度与理想像的对比度的比值为该频率的传递函数值将各种频率的传递函数值作成曲线反映了该视场的成像质量传递函数不能反映光学系统的畸变光学传递函数的评价方法用mtf曲线评价成像质量所有频率用特征频率传递函数值评价光学系统的质量根据光学系统使用目的用mtf阈值进行成像质量评价分辨率用mtf曲线的积分值来评价成像质量中心点亮度用mtf曲线族来进行
光学系统的光学传递函数OTF测定方法理论(实验)研究---终稿

本科毕业设计(论文)光学系统的光学传递函数OT F测定方法理论(实验)研究学 院_ 物理与光电工程学院__专 业_____ 光信息科学与技术_(光电显示与识别技术方向)年级班别________2010级(2)班__学 号_________3110008945______学生姓名___________林清贤___指导教师___________雷 亮____2014 年 4 月 28 日摘要光学传递函数是定量描述成像性能的完备函数。
但是对于实际的光电成像器件(如CCD器件),通过解析法建立这一函数的表达式又是非常困难的,因此光学传递函数的实测技术就显得尤为重要。
光学传递函数是一个客观的、准确的、定量的像质评价指标,并且其能够直接方便的测量,因此已经广泛应用于光学设计、加工、检测和信息处理中。
本文主要介绍了光学传递函数的性质及其测量原理分析,并对固有频率目标法和狭缝扫描法进行了实验研究。
我们采用光学显微镜作为待测量光学传递函数的光学系统,通过改变显微镜的放大倍数,比较分析放大倍数对调制传递函数(MTF)测量的影响,并比较两种测量方法的优劣。
实数傅立叶变换是整个实验中需要透彻理解和运用的数学概念,在此基础上理解离散傅立叶级数与MTF定义的理论依据,并由此建立数学模型。
由本文建立的理论模型出发,结合实验所测得的数据,最后得到了基本可靠的实验结果。
本文最终给出两种测量法对应的matlab程序、数值测量结果、实验测得的可靠的MTF实验结果撰写毕业论文主要内容。
关键字: 光学传递函数,傅立叶变换,固有频率目标法,狭缝扫描法AbstractThe optical transferfunction is quantitatively describe theimag ing performance of the complete function.But for theactual photoel ectric imagingdevices(such asCCD device), through the analytic methodto establishthe function ofexpression is very difficult.Therefore the measurement technique of opticaltransferfunction is particularl yimportant.Opticaltransfer function is an objective, accurate and quantitativeimage quality evaluationindex,anditcan directly andconvenientmeasurement,thereforehasbeen widelyapplied optics design, processing, testing and information processing.This papermainly introducesthe propertiesof theopticaltransfer functionand its measuringprinciple, andthe inherent frequencytarget andslit scanmethod has carried on the experimentalstudy.We us eoptical microscope asfor measuring opticaltransfer function of opti calsystem,through changing the magnificationofthe microscope, comparative analysisof magnification ofmodulation transferfunction (MTF)measurement, theinfluence of themerits ofthe two measuringmethods are compared.Real Fourier transform is the need to thoroughly understand and apply inthe experiment of mathematical concepts, onthebasis of the understanding ofdiscreteFourierseries andth etheoretical basisof the definition of MTF,and thus to establish mathematical model.Set up bythis article onthetheorymodel, combinedwith the data measured inlaboratory, the fundamental and reliableexperiment resultsare obtained.Finally,thepaperproposes two kinds of measurement method of the corresponding matlab program,theresults of numerical measurement andreliableexperimental measured MTFexperimental results of writinggraduation thesis main content.Keywords:Optical transfer function,Fouriertransform,Nat ural frequency method; Slit scan method目录第一章绪论 (1)1.1 光学传递函数简介1ﻩ1.2 光学传递函数的发展1ﻩ1.2.1 光学传递函数的发展历史 (1)1.2.2光学传递函数的发展现状和趋势 (2)1.3光学传递函数的测量意义3ﻩ1.4 本论文的主要内容4ﻩ第二章光学传递函数的基本理论5ﻩ2.1 光学成像系统的一般分析 (5)2.1.1透镜的成像性质5ﻩ2.1.2 光学成像系统的普遍模型 (8)2.1.3 两种类型的物体照明方式9ﻩ2.1.4 阿贝成像理论9ﻩ2.2光学传递函数的概念 ...................................................................................... 102.3光学传递函数的计算ﻩ122.3.1 以物像频谱为基础的计算ﻩ122.3.2以点扩散函数为基础的计算 (13)2.3.3 线扩散函数与一维调制传递函数14ﻩ2.4 离散傅里叶级数与MTF定义的理论依据 ........................................................ 15第三章光学传递函数的测量原理分析 . (18)3.1光学传递函数的测量方法综述18ﻩ3.2 实验中的两种测量方法原理分析 (19)3.2.1 固有频率目标法 (19)3.2.2 狭缝扫描法 ................................................................ 错误!未定义书签。
傅里叶光学金典试题及答案和重要知识点总结

因位置不同而引起的位相色散
x , y
z z
菲涅耳衍射可视为函数
U
0
(
x0
,
y0 ) exp[
j
k 2z
( x0 2
y
0
2
)]
的傅里叶变换在处的值
(3)频域(角谱)表达式: A(u,v) A0 (u,v)exp( jkz)exp[ jz(u2 v2 )]
A(u, v) A0 , • H , H(u,v) exp( jkz)exp[ jz(u2 v2 )] A(u, v) 衍射场角谱 A0 , 孔径后角谱
3、脉冲响应是孔径的傅里叶变换或夫朗和费衍射图样,中心在(-Mx0, -My0)点。 8. 衍射受限系统, 阿贝成像理论;
所谓衍射受限 是指仅仅考虑系统的衍射限制, 不考虑系统的几何像差。
在衍射受限系统中,光的衍射仅受到系统孔径光阑尺寸的限制,因此在考察衍射受限系统时,实际上主要考察
孔径光阑的衍射作用。如果入(出)射光瞳无限大,则光的衍射不受系统的限制,点物应该成理想的点像。然而,
δ 函数的性质:①偶函数性质: (- x) (x) ②坐标缩放性质: (ax) 1 (x)
a
③筛选性质: f (x) (x x0 )dx f (x0 )
④乘积性质: f x• x x0 f x0 • x x0
⑤卷积性质: f x x f x
f x x x0 f x x0
成像过程包含了两次衍射过程:由物面到后焦面,物体衍射光波分解为各种频率的角谱分量,即不同方向传播
的平面波分量,在后焦面上得到物体的频谱。这是一次傅里叶变换过程。由后焦面到像面,各角谱分量又合成为
像,这是一次傅里叶变换逆过程。
9. 相干成像系统的点扩展函数, 相干传递函数; 相干照明系统中,脉冲响应是点物产生的衍射斑的振幅分布。
光学基础

7、F/NO.(F-Number)焦数(相对孔径) F/NO.( Number)焦数(相对孔径)
定义:有效焦距与入射瞳孔径的比值。 F/#=EFL/EPD (EPD:入射瞳孔径) (EPD:入射瞳孔径) 作用:用来决定镜头之明暗。 备注:在保证同样同光孔径的前提下,焦距越短相对孔径应越小。 一般情况下 F/#=2.8,但单片设计时F/#=3.2,N/B Lens F/#=2.8,但单片设计时F/#=3.2, F/#=2.0 F/#越小通光孔径越大。 F/#越小通光孔径越大。
9、RI( Relative Illumination)相对照度 Illumination)相对照度
照度的定义:物体或被照面上被光源照射所呈现的光亮程度称为照 度。 相对照度则是中心照度与外围照度的比值。 注意事项:相对照度过低表现为图像中心较亮,而四周较暗,即渐 晕现象,俗称暗角(Shading)。相对照度过低还会导致色彩失真。 晕现象,俗称暗角(Shading)。相对照度过低还会导致色彩失真。 RI与COS4 (semi-FOV)成正比:RI∝COS4 (semi-FOV) RI与 (semi-FOV)成正比:RI∝ (semiSemi-FOV=30°,从理论上RI<56% Semi-FOV=30°,从理论上RI<56% Semi-FOV=35°,从理论上RI<45% Semi-FOV=35°,从理论上RI<45% 当RI<50%时人眼是能分辨的,严重时会出现画面四角全黑的“缺 RI<50%时人眼是能分辨的,严重时会出现画面四角全黑的“缺 角”现象。 因此RI的基本要求为:RI>50% 因此RI的基本要求为:RI>50%
8、Distortion 畸变
畸变是轴外相差。而且是轴外细光束的像差。它是轴外点与主光线 在像面上交点的高度同理想(近轴)像面的高度差。它是视场的函数, 与孔径没有关系,初级畸变随视场(像高)的三次方变化,而百分比 畸变随像高平方增加,所以视场不同畸变也不同。畸变的变化不是线 性的,仅是像的变形,不影响像的清晰度。 畸变分为TV畸变和光学畸变两种:TV畸变: TV畸变分为TV畸变和光学畸变两种:TV畸变: TV-Distortion 光学畸变:Optical-Distortion 光学畸变:OpticalTV畸变分为枕型与筒型两种。 TV畸变分为枕型与筒型两种。 Vertical)TV)/2(Vertical)TV-Distortion=[(V1+V2)/2-Y]/Y*100% (Horizontal)TV-Distortion=[(H1+H2)/2-X]/X*100% Horizontal)TV)/2注意事项: 畸变是用户很容易感觉到的成像质量。 畸变是用户要求很严的镜头指标, OpticalOptical-Distortion<3% 人眼不容易察觉 OpticalOptical-Distortion<2% 摄影物镜的畸变要求 CIF TV-Distortion<2.0% TVVGA TV-Distortion<1.5% TV1.3M/2.0M/3.0M TV-Distortion<1% TV-
Unit11 传递函数和拉普拉斯变换

Unit11 传递函数和拉普拉斯变换传递函数若已知图2-1所示线性系统的输入输出关系,该系统的特点也就知道了。
在拉普拉斯域里输入输出关系叫做传递函数(TF或者G增益)。
通过定义,一个元件或系统的传递函数是输入的拉氏变换形式与输出的拉氏变换形式的配给量:公式2-1这个传递函数的定义要求系统是线性的和定常的,并且有连续的变量和零初始状态。
当系统有多个参数并且缺少或忽略传输延迟时,这个传递函数是最有用的。
在这些条件下传递函数可被表示为两个关于复拉普拉斯变量s的多项式之比,或者Function(式2-2)。
对于物理系统,自然特性通常为积分形式而不是微分形式,故N(s)比D(s)的阶数低。
在传递函数中将拉普拉斯变量s用jωt代替可得到在频域中使用的频率传递函数(FTF),稍后将会被表示出来。
在式2-2中,传递函数的分母D(s)称为特征函数,因为它包含了系统所有的物理特性。
特征方程由令D(s)等于0得到。
特征方程的根决定了系统的稳定性和任何输入的暂态响应的一般特性。
分子多项式N(s)是一个反映输入如何进入系统的函数。
因此,N(s)和特定的输入一起决定了每个暂态模式的大小和符号,并且建立了暂态响应的模型以及输出稳态值。
对于一个闭环系统,传递函数为:公式2-3其中W(s)是闭环传递函数,G(s)H(s)成为开环传递函数,1+ G(s)H(s)是特征函数。
传递函数可通过几种方法得到。
一种方法是将描述元件或系统的微分方程进行拉普拉斯变换并解出传递函数,这种方法是单纯的数学方法,仅由拉普拉斯变换和非零初始条件组成,非零初始条件将作为额外输入。
第二种方法是根据实验得出的。
一个已知输入(通常用正弦输入或阶跃输入)应用于系统时,测量输出,则传递函数由操作数据和已知的个别元件的传递函数的组合构成。
这种组合或归纳过程叫做代数方程图。
拉普拉斯变换拉普拉斯变换来自工程数学领域,在分析和设计线性系统时非常有用。
普通的具有常数系数的微分方程转换为可求得传递函数的代数方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
c
上述分析得到结论:在相干光照明下,此成像系统不允许该物函数的
基频及以上的频率通过,只能让零频分量通过。所以物不能成像,像面上 是均匀强度分布。
非相干光照明下,系统的截止频率为
2cຫໍສະໝຸດ 2 b所以零频和基频都能通过系统参与成像。尽管像的基频被衰减,高频被截
b a
M ,
综合上式,有
Vi Vg M , 说明对比度下降了!
另外, i , g , , 表明产生了条纹错开!
由此可见,OTF描述了像与物的对比度的比较, 以及相位改变的多少。因此,OTF表征了非相干光 学系统成像质量的好坏。
非相干光照明下,
像的强度为
Ii I g hI
像强度的频谱为 Gi , Gg , Gg , H , H ,
举例分析两种情况下的像强度
物体的复振幅透过率为 t1x cos 2
x b
,将此物通过一个
横向放大率为1的光学系统成像,系统的出瞳是半径为a 的圆
V
Imax I min
I max I min
计算余弦函数输入物和输出像的对比度,得
a b a b b Vg a b a b a
Vi
a a
bM , bM ,
a a
bM , bM ,
dd
令 di x , di y ,有
Η
,
Px,
yPx di , y di
Px, y2 dd
dxdy
Px, yPx di , y di dxdy Px, ydd
即 Η , S ,
光学传递函数 OTF
对于非相干光照明下的衍射受限系统,表征系统的成像质量的 指标就是光学传递函数。
非相干成像系统是强度的线性空不变系统(LSI)。
一. 非相干光照明下,衍射受限系统的成像规律
1. 物像关系(空域中)
Ii xi , yi k I g ~x0 , ~y0 hI xi ~x0 , yi ~y0 d~x0d~y0
H , 称为光学传递函数。它等于像面强度频谱
与物面强度频谱之比。
光学传递函数(OTF)有3种表达式:
1. 定义式
Η
,
HI , HI 0,0
hI
xi ,
yi
exp j2 xi yi
hI xi , yi dxidyi
dxidyi
S0
说明:分母是光瞳的总面积; 分子是两个错开的光瞳的重叠面积。
1. OTF的几何计算
如图:
y
O
x
光瞳的总面积 S 0
y
O
x
di
重叠面积 S ,
di
注:重叠面积指中心在(0,0)的原光瞳与平移到中心
在 di ,di 的光瞳的重叠部分。
2. OTF的性质
(1) Η , 是实的非负函数,说明在非相干光照明
l l
当 Px, y 在 x, y 方向分别位移 得到 Px di , y di
di ,di
后,
重叠面积的计算:
光瞳总面积: S0 l 2
动态分析图
当di l或di l时,
S , 0
当di l并且di l时,
kIg xi , yi hI xi , yi
其中 hI xi , yi 称为强度脉冲响应.
hI xi ,
yi
h~xi ,
2
yi
它表示点物产生的像斑的强度分布。
2. 物像关系(频域中)
Gi , Gg , H I ,
其中
Gi , FT Ii xi , yi
2
所以,在截止频率内,光学传递函数为
H ,0 S ,0 2 sin cos
S0
OTF计算——EXAMPLE 3
OTF的计算公式
相干成像和非相干成像的比较
从照明光、截止频率、像强度的频谱和两点的分 辨等方面对这两种成像进行比较。
相干成像 (相干光照明)
I g ~x0 , ~y0 a b cos 2 0~x0,0 ~y0 g 0 ,0
Ii xi , yi a bM cos 2 0xi ,0 yi g , ,
振幅改变
产生相移,即相位改变
对比度(调制度)的定义
一个像的视觉质量很大程度依赖于“反衬度”。换句话说: 视觉质量依赖于像的携带信息的部分相对于本底的相对强度。
什么是归一化处理? 例如:测量单缝衍射光强分布曲线,测量值是I,I
的最大值是I 0。 我们作图时,经常的处理方法是计算 I / I 0,以它作为 纵坐标的值。这就是归一化处理。
I 0 1
d 形为孔照径明,光并波且波长bd,i 请a 问2对bdi该。物体i 成为像出,瞳采到用像相面干的光距和离非,相 干
光照明,哪一种方式更好?
分析:首先,该系统的出瞳是圆孔,
相干光照明时,其截止频率为
c
a
di
又因为题目给出了条件: di a 2di
b
b
,所以得到
1 2
c
di
1
di
l
1
di
l
1
l
/
d
i
1
l
/ di
l
/ di
l
/ di
同一系统的相干传递函数的截止频率为
c
l
2d i
由此可见,光学传递函数的截止频率是
的自相关归一化函数。
等于相干传递函数
衍射受限系统的OTF的计算
对于同一个衍射受限系统,有相干传递函数 H , Pdi , di
所以光学传递函数为
Η
,
Pdi, di Pdi , di
Pdi,di 2 dd
叠面积为零。即 H , 0 。物理意义是,在截止频
率规定的范围之外,光学传递函数为零,像面上不出现这些 频率分量。
OTF的计算
首先,利用傅立叶光学来研究光学系统的成像特 性,产生了传递函数的概念。
光学成像系统的光瞳反映了系统对光束的限制。 因此,即使不考虑几何光学像差的情况下,系统由于 存在衍射效应,它也不可能理想成像——点物成点像。 从傅立叶光学的观点来看,系统的光瞳限制了物面的 频谱向像面的传递,因此系统不可能理想成像。
Gg , FT I g xi , yi
H I , FT hI xi , yi
3. 归一化频谱关系式
本
底
本
色
底
色
Fig. 1
Fig. 2
使用归一化频谱的原因:强度是一个非零值,I 0 。反映
在一幅图上,光强度的变化就是灰度的变化。
强度的分布总是有一个非零的“直流分量”或“本底”。
1 b
c
(1)
接着,将物函数分解为余弦函数的线性组合,即将其展开成傅立叶级数,得
tix
cos 2
x b
4
1
2
1 cos 4 13
x b
1 cos 6 35
x b
由此式可知,此物的基频为2/b 。
由 (1) 式 得2 b
取值范围: M , 1
相位传递函数(Phase Transfer Function ,PTF):描 述了系统对各频率分量施加的相位移动。
对OTF的理解
因为余弦函数是线性空不变系统(LSI)的本征函数,即有
f x, y aLf x, y
Ig
物
Ii
经过成像系统
像
x0
xi
非相干成像 (非相干光照明)
备注
截止 频率
c
l
2d i
2c
l
di
能否就此判断“非相 干成像比相干成像的 效果好”呢?
像强度 Ii xi , yi Ui xi , yi 2 的频谱 U g xi , yi h~xi , yi 2 Ii xi , yi I g xi , yi hI xi , yi
I0
设 Gi , Gg , H I , 的零频分量分别为:
Gi 0,0 Gg 0,0 H I 0,0
对上述三个量进行归一化处理,有:
Gi , G g ,Η ,
则有:
Η
,
Gi Gg
, ,
dxi dyi
FThI xi , yi
hI xi , yi dxidyi
FT h~xi , yi 2 h~xi , yi 2 dxidyi
H
, H , H , 2 dd
H H 说明:对于同一个系统来说,光学传递函数
两点 分辨
依赖两个点光源的相 使用瑞利判据 位关系
(1)截止频率
OTF的截止频率是CTF的截止频率的两倍,并不 意味非相干照明比相干照明好。
原因:
相干截止频率确定像的振幅的最高频率分量; 非相干截止频率确定像的强度的最高频率分量。 这两者不能直接比较。
H ,
1
D 2d i
