数学椭圆双曲线抛物线的公式大全
高中数学有关圆-椭圆-双曲线-抛物线的详细知识点

<一>圆的方程(x-a)^2+(y-b)^2=r^2,圆心O(a,b),半径r。
(1)圆的一般式方程:x^2+y^2+Dx+Ey+F=0此方程可用于解决两圆的位置关系:配方化为标准方程:(x+D/2)^2.+(y+E/2)^2=(D^2+E^2-4F)/4其圆心坐标:(-D/2,-E/2)半径为r=√[(D^2+E^2-4F)]/2此方程满足为圆的方程的条件是:D^2+E^2-4F>0若不满足,则不可表示为圆的方程(2)点与圆的位置关系点P(X1,Y1) 与圆(x-a)^2+(y-b) ^2=r^2的位置关系:⑴当(x1-a)^2+(y1-b) ^2>r^2时,则点P在圆外。
⑵当(x1-a)^2+(y1-b) ^2=r^2时,则点P在圆上。
⑶当(x1-a)^2+(y1-b) ^2<r^2时,则点P在圆内。
圆与直线的位置关系判断平面内,直线Ax+By+C=0与圆x^2+y^2+Dx+Ey+F=0的位置关系判断一般方法是:1.由Ax+By+C=0,可得y=(-C-Ax)/B,(其中B不等于0),代入x^2+y^2+Dx+Ey+F=0,即成为一个关于x的一元二次方程f(x)=0。
利用判别式b^2-4ac的符号可确定圆与直线的位置关系如下:如果b^2-4ac>0,则圆与直线有2交点,即圆与直线相交。
如果b^2-4ac=0,则圆与直线有1交点,即圆与直线相切。
如果b^2-4ac<0,则圆与直线有0交点,即圆与直线相离。
2.如果B=0即直线为Ax+C=0,即x=-C/A,它平行于y轴(或垂直于x 轴),将x^2+y^2+Dx+Ey+F=0化为 (x-a)^2+(y-b) ^2=r^2。
令y=b,求出此时的两个x值x1、x2,并且规定x1<x2,那么:当x=-C/A<x1或x=-C/A>x2时,直线与圆相离;当x1<x=-C/A<x2时,直线与圆相交;半径r,直径d在直角坐标系中,圆的解析式为:(x-a)^2+(y-b)^2=r^2;x^2+y^2+Dx+Ey+F=0=> (x+D/2)^2+(y+E/2)^2=(D^2+E^2-4F)/4=> 圆心坐标为(-D/2,-E/2)其实只要保证X方Y方前系数都是1就可以直接判断出圆心坐标为(-D/2,-E/2)这可以作为一个结论运用的且r=根号(圆心坐标的平方和-F)<二>椭圆的标准方程椭圆的标准方程分两种情况:当焦点在x轴时,椭圆的标准方程是:x^2/a^2+y^2/b^2=1,(a>b>0);当焦点在y轴时,椭圆的标准方程是:y^2/a^2+x^2/b^2=1,(a>b>0);其中a>0,b>0。
圆椭圆双曲线抛物线知识点汇总

圆椭圆双曲线抛物线知识点汇总一、圆椭圆双曲线抛物线的定义1. 圆:圆是平面上到定点距离相等的所有点的集合。
圆由圆心和半径唯一确定。
2. 椭圆:椭圆是平面上到两个定点的距离之和为常数的所有点的集合。
椭圆由两个焦点和两个半轴唯一确定。
3. 双曲线:双曲线是平面上到两个定点的距离之差为常数的所有点的集合。
双曲线由两个焦点和两个实轴唯一确定。
4. 抛物线:抛物线是平面上到定点距离等于到定直线的距离的所有点的集合。
抛物线由焦点和直线唯一确定。
二、圆椭圆双曲线抛物线的方程1. 圆:圆的标准方程为(x-a)² + (y-b)² = r²,其中圆心为(a, b),半径为r。
2. 椭圆:椭圆的标准方程为x²/a² + y²/b² = 1,其中a和b分别为x轴和y轴上的半轴长。
3. 双曲线:双曲线的标准方程为x²/a² - y²/b² = 1或者y²/a² - x²/b² = 1,取决于焦点的位置。
4. 抛物线:抛物线的标准方程为y² = 4ax或者x² = 4ay,取决于抛物线开口的方向。
三、圆椭圆双曲线抛物线的性质1. 圆:圆的直径是圆上任意两点之间的最大距离,且所有直径相等。
2. 椭圆:椭圆的离心率介于0和1之间,离心率越接近0,椭圆越接近于圆。
3. 双曲线:双曲线分为两支,每一支的焦点到定点的距离之差相等。
4. 抛物线:抛物线的焦点在抛物线上方,开口方向取决于系数a的正负号。
四、圆椭圆双曲线抛物线的应用1. 圆:在几何中常常与角度和三角函数结合,用于描述正弦和余弦函数的周期性。
2. 椭圆:在天体力学中用于描述行星轨道的形状,以及通信中的极化椭圆。
3. 双曲线:在光学和电磁学中用于描述折射和反射现象。
4. 抛物线:在物理学中用于描述自由落体运动和抛物线运动。
椭圆、双曲线、抛物线知识总结

一.椭圆二.双曲线四.椭圆、双曲线及抛物线的性质对比(焦点在x轴上)名称椭圆双曲线抛物线定义|PF1|+|PF2|=2a(2a>|F1F2|)||PF1|-|PF2||=2a(2a<|F1F2︱)|PF|= 点F不在直线l上,PM⊥l于M标准方程12222=+byax(a>b>0)12222=-byax(a>0,b>0)y2=2px(p>0)图象几何性质范围byax≤≤,ax≥0≥x顶点),0(),0,(ba±±)0,(a±(0,0)对称性关于x轴,y轴和原点对称关于x轴对称焦点(±c,0 ))0,2(p轴长轴长2a,短轴长2b实轴长2a,虚轴长2b准线cax2±=2px-=通径abAB22=pAB2=渐近线xaby±=...——知识就是力量,学海无涯苦作舟!——不要担心知识没有用,知识多了,路也好选择,也多选择。
比如高考,高分的同学,填报志愿的时候选择学校的范围大,而在分数线左右的就为难了,分数低的就更加不要说了。
再比如,有了知识,你也可以随时炒老板。
圆锥曲线的标准方程公式

圆锥曲线的标准方程公式
圆锥曲线的标准方程公式是数学中用于描述圆锥曲线几何性质的方程形式。
圆锥曲线包括圆、椭圆、双曲线和抛物线。
每种曲线都有其独特的标准方程形式。
1. 圆的标准方程公式:
圆的标准方程公式是(x - h)² + (y - k)² = r²,其中圆心坐标为(h, k),半径为r。
这个方程描述了平面上所有到圆心距离等于半径的点的集合。
2. 椭圆的标准方程公式:
椭圆的标准方程公式是(x²/a²) + (y²/b²) = 1,其中a和b分别代表椭圆的长轴
和短轴的半长。
这个方程描述了平面上到椭圆两个焦点的距离之和等于常数2a的
点的集合。
3. 双曲线的标准方程公式:
双曲线的标准方程公式可以分为两种形式:(x²/a²) - (y²/b²) = 1和(y²/a²) - (x²/b²) = 1,其中a和b分别代表双曲线的焦点到中心的距离和横轴/纵轴的半长。
这个方
程描述了平面上到双曲线两个焦点的距离之差等于常数2a的点的集合。
4. 抛物线的标准方程公式:
抛物线的标准方程公式可以分为两种形式:y² = 4ax和x² = 4ay,其中a为抛物线的焦点到顶点的距离。
这个方程描述了平面上到抛物线焦点的距离等于焦点到顶点距离的某个倍数的点的集合。
通过这些标准方程公式,我们可以方便地描述和理解圆锥曲线的形状和性质。
它们在几何、物理、工程等领域中都有广泛的应用。
二次曲线离心率万能公式(一)

二次曲线离心率万能公式(一)二次曲线离心率万能公式1. 引言二次曲线是数学中一个重要的概念,它在几何学、物理学和工程学等领域中都有广泛的应用。
离心率是二次曲线的一个重要参数,它可以反映出二次曲线的形状和偏心程度。
在本文中,我们将介绍二次曲线离心率的万能公式,包括椭圆、双曲线和抛物线的计算公式,并举例说明它们的应用。
2. 椭圆的离心率公式椭圆是一种闭合的曲线,其形状类似于圆形。
椭圆的离心率公式如下:e = sqrt(1 - (b^2 / a^2))其中,e为椭圆的离心率,a为椭圆的长轴长度,b为椭圆的短轴长度。
例如,对于一个椭圆,它的长轴长度为6,短轴长度为4。
我们可以使用上述公式计算其离心率:e = sqrt(1 - (4^2 / 6^2)) = sqrt(1 - (16 / 36)) = s qrt(1 - ) ≈因此,该椭圆的离心率约为。
3. 双曲线的离心率公式双曲线是一种开口向上或向下的曲线,其形状类似于抛物线。
双曲线的离心率公式如下:e = sqrt(1 + (b^2 / a^2))其中,e为双曲线的离心率,a为双曲线的距离中心最远点的距离(也称为焦距),b为双曲线的顶点到焦点的距离。
举个例子,假设我们有一个双曲线,其距离中心最远点的距离为4,顶点到焦点的距离为2。
根据上述公式,我们可以计算其离心率:e = sqrt(1 + (2^2 / 4^2)) = sqrt(1 + (4 / 16)) = sq rt(1 + ) ≈因此,该双曲线的离心率约为。
4. 抛物线的离心率公式抛物线是一种开口向上或向下的曲线,其形状类似于双曲线。
抛物线的离心率公式如下:e = 1抛物线的离心率始终为1,与其形状无关。
5. 总结二次曲线离心率万能公式是一个简单而实用的工具,可以用来计算椭圆、双曲线和抛物线的离心率。
通过离心率的计算,我们可以了解二次曲线的形状和偏心程度,从而更好地理解和应用二次曲线的相关知识。
高考数学:专题五 第二讲 椭圆、双曲线、抛物线课件
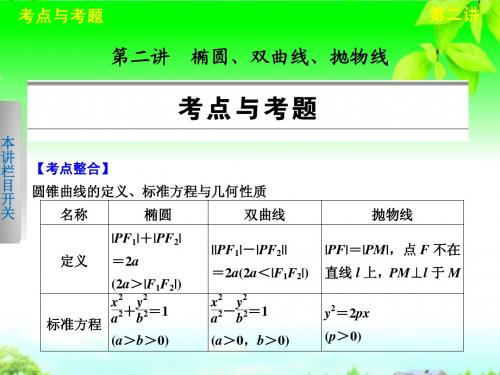
考点与考题
第二讲
本 讲 栏 目 开 关
图形
考点与考题
范围 顶点 对称性 |x|≤a,|y|≤b (± a,0)(0,± b) |x|≥a (± a,0) x≥0 (0,0)
第二讲
关于 x 轴,y 轴和原点对称 (± c,0) 长轴长 2a, 短轴长 2b c e=a b2 = 1- 2 a (0<e<1) 实轴长 2a, 虚轴长 2b c e=a b2 = 1+ 2 a (e>1)
解析 由 x2-y2=2 知,a2=2,b2=2,c2=a2+b2=4,
∴a= 2,c=2.
又∵|PF1|-|PF2|=2a,|PF1|=2|PF2|,
∴|PF1|=4 2,|PF2|=2 2.
又∵|F1F2|=2c=4,
4 22+2 22-42 ∴由余弦定理得 cos∠F1PF2= 2×4 2×2 2 3 = . 4
∴直线 AF 的方程为 y=2 2(x-1). y=2 2x-1, 联立直线与抛物线的方程 2 y =4x,
1 x=2, x= , 2 解之得 或 y=2 2. y=- 2 1 由图知 B2,- 2,
考点与考题
1 1 ∴S△AOB= |OF|· A-yB|= ×1×|2 2+ 2| |y 2 2 3 = 2.故选 C. 2
答案 2 7-5
题型与方法
第二讲
方法提炼 何性质.
研究圆锥曲线的几何性质,实质是求参数a、b、c或者
建立a、b、c的关系式(等式或不等式),然后根据概念讨论相应的几
本 讲 栏 目 开 关
题型与方法
第二讲
本 讲 栏 目 开 关
变式训练 2 (1)若点 P 为共焦点的椭圆 C1 和双曲线 C2 的一个交点, F1、F2 分别是它们的左、右焦点,设椭圆离心率为 e1,双曲线离心率 1 1 → → 为 e2,若PF1· 2=0,则 2+ 2等于 PF (B ) e1 e2 A.1 B.2 C.3 D.4
(完整版)圆、椭圆、双曲线公式大全
圆锥曲线公式大全项目概念性质方程位遥关系图形Cl )⅛ n + r s > ∣O1C ⅛∣时俩 删外寓 i(Z)ALi n + n= 10161时,两 風外切⑶当 ∣n-n ∣< ∣O ∣O i ∣<r 1 ÷n 时,两圆相交 ⑷ ⅛ Irl -FJI = Iolo ⅛ I 时.两 侧内切 ⑸当 Ir l -^I <∣OAIH 两 圆内普若圆 Cl S X 2÷y ι+l>∣jr÷fi]y+ Fl=JO f∏l ⅛ Cj : r 34 v∏ Z ⅛ + ⅛y+F 1- O 相交•则公井痣所在直线的方桎是(DI--D? )r 十(/<[ —EE)JH F 1 — Z ?2 —O(三)椭圆 衣1椭01的基本概念和性质 项目 概念性质图形椭闘址SL 1平面内到两个定点D 的距离 的和^i-⅛⅛(ΛΓIFJ ⅛∣>的直的轨迹*叫做椭團•其 中 两,运点F,.∕½∏qf ⅛ffiii ⅛∣的勲点 两焦点间的即.离叫做椎侧的建距 I 换言之*椭圆就是点集 IMl IMFI I+ IΛfF i I ≡2α・ 2⅛>∣F ∣Γ1 ∣,α J ⅛ttft}绩表圆的切 点弦 圆的切点⅛切点曲 方悸自卿外说引圆的两 条切线•切点的连线叫做点Cn * M )矣F 圆的切点弦点5 P α》关于恻+ + J√ ■ r 1 的切点戎所在胚线的方程浪 z⅛r+v ∣)V~r r>lH-⅛SI 的位进)&系那交罔的右 并眩所在直浅的方程在2 对祢轴平行坐标4⅛的#⅛嵐项且 概念性质方程图形椭岡宦义1 —点集{M ∣ IMF] I 于 IMF 訂=加,%>1F1F 訂}椭圆定义2-一_ L点集{Afl 点肚到仏的距?⅛ YoKI }___________________ _ ___________________中心在原点 的标准方程 千 +書=IaAQnΛi* h γ'图形Λy44IWB I.rt'2k =-般方∙P≡/Lr i÷C√=X(j 4.C ∖∕C 同号)绫表桶劃的逋 径和焦参数过煤点且垂直于长铀的弦叫 WSIH ⅛⅛通径逋径长度之字叫做榔圆的址 螯数橢恻的焦 点半径箭圆上一点厂和櫛圆鄭点的 连线叫做点P 的焦点半轻.也叫 焦半径椭同的 准线范 t⅛圆的两条准线的距离叫做 准线距焦准距 l⅛岡的焦点句梱应醸线闸的 I 距薦叫做焦准艷项目 槪念 性质概念分祈讨论画法Li 知上葩初住的焦奪数尸 求作:抛物纯•使F 为焦 虫■屮Kl=T \址A :的宜纯 LLFJC 作法丄作直线Mg 在 MN 上截 FK,便 IFXI = P^ii K 布臣线儿使J 丄 JU N ® /丄FK 几取FK 的 中点OlOgtft 抛物线的顶 J 7 2- ⅛αv 上枉取…点儿•过儿 作/的平行线、以F 为妙A KH ]为半径柞弧衰过儿的平行线于点P ∣4P ,1 ⅛⅛Λ1的位 置雄ON 上取点 用同样的方法可得剑点P 屛F J 尸 JFV “ 3 ■用平滑的曲线硕次连结"YShdgOdPdFl …,就 得到葩物线 续表W的法抛线渦 圆锥曲线的画堆。
高中数学知识点---椭圆、双曲线、抛物线
高中数学专题四椭圆、双曲线、抛物线《圆锥曲线》知识点小结一、椭圆:(1)椭圆的定义:平面内与两个定点21,F F 的距离的和等于常数(大于||21F F )的点的轨迹。
其中:两个定点叫做椭圆的焦点,焦点间的距离叫做焦距。
注意:||221F F a >表示椭圆;||221F F a =表示线段21F F ;||221F F a <没有轨迹; (2)椭圆的标准方程、图象及几何性质:3.常用结论:(1)椭圆)0(12222>>=+b a by a x 的两个焦点为21,F F ,过1F 的直线交椭圆于B A ,两点,则2ABF ∆的周长=(2)设椭圆)0(12222>>=+b a by a x 左、右两个焦点为21,F F ,过1F 且垂直于对称轴的直线交椭圆于Q P ,两点,则Q P ,的坐标分别是 =||PQ二、双曲线:(1)双曲线的定义:平面内与两个定点21,F F 的距离的差的绝对值等于常数(小于||21F F )的点的轨迹。
其中:两个定点叫做双曲线的焦点,焦点间的距离叫做焦距。
注意:a PF PF 2||||21=-与a PF PF 2||||12=-(||221F F a <)表示双曲线的一支。
||221F F a =表示两条射线;||221F F a >没有轨迹;(2(3)双曲线的渐近线:①求双曲线12222=-b y a x 的渐近线,可令其右边的1为0,即得02222=-by a x ,因式分解得到0x ya b±=。
②与双曲线12222=-b y a x 共渐近线的双曲线系方程是λ=-2222y x ;(4)等轴双曲线为222t y x =-2(4)常用结论:(1)双曲线)0,0(12222>>=-b a by a x 的两个焦点为21,F F ,过1F 的直线交双曲线的同一支于B A ,两点,则2ABF ∆的周长=(2)设双曲线)0,0(12222>>=-b a by a x 左、右两个焦点为21,F F ,过1F 且垂直于对称轴的直线交双曲线于Q P ,两点,则Q P ,的坐标分别是=||PQ三、抛物线:(1)抛物线的定义:平面内与一个定点的距离和一条定直线的距离相等的点的轨迹。
8.12椭圆、双曲线、抛物线的统一定义
8.7椭圆、双曲线、抛物线的统一定义1.椭圆、双曲线、抛物线的统一定义是在平面上,若动点 M 与一个定点F 及M 到一条定直线(定点 M 不在定直线上)距离之比等于常数 f ,当0<e <i 时,点M 的轨迹是椭圆;当 e >i 时,点M 的轨迹为双 曲线;当e = 1时,点M 的轨迹为抛物线.2 22 .椭圆 笃+当=1(a Ab>0)上点 M ( x 0,y 0)的左焦点半径+ ,右焦点半径a bx 2y2MF ?] =a —ex o ,椭圆手 p =1(a >b >0)上点P ( X o , y o )的下焦点半径 PF 』=a + ey °,上焦点 a b半径PF 2 =a-ey o .希望注意双曲线的焦半径与椭圆的焦半径的区别.2 2X y3•双曲线— 牙=1上一点P ( X o ,y o )的焦半径公式a b(1) x o >o , PF l=ex )+a , PF^ex^ - a ;(2) X o <o , PF 1 = —(ex o + a), PF 2 — —(ex o — a).4 .抛物线y 2二2px(p o)和抛物线x 2二2py(p o)的焦半径公式:如图所示,已知椭圆C 的焦点是3,o ), F 2C 3,0),点F 1到相应的准线的距离为 过F 2点且倾斜角为锐角的直线 l 与椭圆C 交于A 、B 两点,使得,F 2B =3F 2A .(1)求椭圆C 的方程;(2)求直线l 的方程.PFPFy o •卫2、-3 3例2 已知双曲线b2x2- a2y2=a2b2的离心率的取值范围为e (1 • 2, •::),左、右焦点分别为F2,左准线为丨,能否在双曲线的左支上找到一点P,使得PF1是P到丨的距离d与PF2的等比中项?例3 如图所示.有一张长为8,宽为4的矩形纸片ABCD ,按图示的方法进行折叠,使每次折叠后点B都落在AD边上.此时将B记为B'(注:图中FE为折痕.点F也可落在边CD 上).过B'作B '// CD交EF于点T .求点T的轨迹方程.已知线段AB的两个端点在椭圆2 2—-红=1上滑动,且25 1632AB = m(——c m £10),5M为AB的中点,求M到y轴的最大距离.I1例6一动点到定直线 X = 3的距离是它到定点 F ( 4,0)的距离的-,求这个动点的轨迹方程.28.12椭圆、双曲线、抛物线的统一定义证:2 2例5 已知AB 是双曲线 冷一仝=1(a .o,b .0)过右焦点a 2b 21 AF ,1 BF ,为定值,并求出该定值.1-已知双曲线A m 2x 2=1(m >°)的一个顶点到它的一条渐近线的距离为5,则m=C . 3最小值为4MF +5MA 的最小值为最大值为 _________________解答题2.已知点P 是抛物线y 2 = 2x 上的一个动点,则点P 到点(0,2)的距离与 P 到该抛物线准线的距离之和的3.已知抛物线y 2= 2px (p>0),过焦点且斜率为 坐标为2,则该抛物线的准线方程为1的直线交抛物线于 A 、 B 两点,若线段 AB 的中点的纵A . x = 1 C . x = 2 D . x =- 24.过原点的直线B . x =- 12 2I 与双曲线x -73 =- 1交于两点,则直线l 的斜率的取值范围是4 3一亜一 2,-m ,-舟U 于,+o25. 设P 是双曲线x 2-= 1的右支上的动点,F 为双曲线的右焦点,已知 3A ( 3,1),则 |FA|+ |PF|的最小值为 ________ . 6. 如图,抛物线顶点在原点,圆 x 2+ y 2- 4x = 0的圆心恰是抛物线的焦点.(1) ______________________ 抛物线的方程为 ; (2) 一直线的斜率等于 2,且C 、D 四点,贝U |AB|+ |CD| = ________ .2 2x V7.已知椭圆的方程是 — 1(a 5),它的两个焦点分别为F 、F ,且F 1 F 2 =8,弦 AB 过 F ],则△ AB F 2的周长为 ___________________________&若点A 的坐标为(3, 2), F 为抛物线y 2 =2x 的焦点,点P 是抛物线上一动点,则 PA+|PF 取得最 小值时点P 的坐标是 ________________________________ .9.已知点F 为双曲线2 2x y 169=1的右焦点, M 是双曲线右支上一动点,定点 A 的坐标是(5, 1),则10. P ( x, y )是椭圆2 2X . y a 2b 2= 1(a b 0)上任意一点, F 1> F 2是它的左、右焦点,则PF 1 PF 2 的一oo,,C .2 2y x11 •如图所示,M ,N 是椭圆C l :22=1(a b ■ 0)的一条弦,A (1, -2)a b是MN 的中点,以A 为焦点,以椭圆 C 2的下准线丨为相应准线的双曲线 C 2与直 线MN 交于点B (- l ,- 4),设曲线 G, C 2的离心率分别为 e ,,e 2 •(1) 试求e 1的值,并用a 表示双曲线的离心率 e 2 ; (2) 当e )e 2 =1时,求MB 的值.2 2x y2 212 •如图,点P(0,-1)是椭圆2=1(a b 0)的一个顶点,G 的长轴是圆C 2:x y =4的直a b(1) 求椭圆G 的方程;(2) 求 ABD 面积取最大值时直线|1的方程.径• 11 ,1 2是过点P 且互相垂直的两条直线,其中h 交圆C 2于两点,12交椭圆G 于另一点D(第12题图)。
数学双曲线公式
数学双曲线公式数学双曲线是一类在平面上呈现出特定形状的曲线。
它们在数学和物理学中具有重要的应用,如椭圆、双曲线和抛物线。
在本文中,我们将重点介绍双曲线的公式以及它们的性质。
双曲线的一般方程可以写成以下形式:(x^2/a^2) - (y^2/b^2) = 1其中a和b是正实数,控制着双曲线的形状。
这个方程描述了一个以原点为中心的双曲线,其中x轴和y轴是对称的。
双曲线有两个分支,分别向左右延伸无限远。
由于其形状的特殊性,双曲线具有许多独特的性质。
首先,双曲线的焦点是其最重要的特征之一。
焦点是与双曲线上的点P到两个直线的距离之差的绝对值等于常数2c的点F1和F2。
这个常数c可以通过以下公式计算得到:c = √(a^2 + b^2)其次,双曲线还有两个渐近线。
渐近线是与双曲线趋于无限远处的直线,与双曲线的距离趋于零。
双曲线的渐近线可以通过以下公式计算得到:y = ± (b/a) * x双曲线还具有一些其他的重要性质,如双曲线的离心率。
离心率是一个描述双曲线形状的参数,可以通过以下公式计算得到:e = c/a离心率越大,双曲线的形状越扁平;离心率越小,双曲线的形状越尖锐。
双曲线在许多领域中都有广泛的应用。
在物理学中,双曲线可以描述光学器件的形状,如抛物面镜和双曲面镜。
在工程学中,双曲线可以用来设计天线和椭圆轨道。
在经济学中,双曲线可以用来描述消费者的选择和偏好。
总之,双曲线是一类重要的数学曲线,具有独特的形状和性质。
了解双曲线的公式和性质可以帮助我们更好地理解和应用这些曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
下面是数学中椭圆、双曲线和抛物线的标准方程和参数方程的公式大全:
椭圆(Ellipse): 标准方程:(x-h)^2/a^2 + (y-k)^2/b^2 = 1 (a > b) 参数方程:x = h + a cos(t), y = k + b sin(t), (0 ≤ t < 2π)
双曲线(Hyperbola): 标准方程:
1.纵轴为主轴(竖直方向):(y-k)^2/b^2 - (x-h)^2/a^2 =
1 (a > b)
2.横轴为主轴(水平方向):(x-h)^2/a^2 - (y-k)^2/b^2 =
1 (a > b) 参数方程:
3.纵轴为主轴(竖直方向):x = h + a cosh(t), y = k +
b sinh(t), (t为实数)
4.横轴为主轴(水平方向):x = h + a sinh(t), y = k +
b cosh(t), (t为实数)
抛物线(Parabola): 标准方程:
1.焦点在y轴上:y^2 = 4px
2.焦点在x轴上:x^2 = 4py 参数方程:
3.焦点在y轴上:x = pt^2, y = 2pt, (t为实数)
4.焦点在x轴上:x = 2pt, y = pt^2, (t为实数)
在这些公式中,(h, k) 是中心的坐标,a 和b 是椭圆或双曲线的半轴长度,p 是焦点到准线的距离,且p > 0。
椭圆和双曲线有两个焦点,而抛物线只有一个焦点。
这些公式是椭圆、双曲线和抛物线的基本形式,可以根据具体的问题和已知条件进行适当的变换和调整。
请注意,这些公式适用于笛卡尔坐标系,如果使用其他坐标系,可能需要进行适当的转换。
