高二数学参数方程
高考数学知识点参数方程

高考数学知识点参数方程高考数学知识点:参数方程数学在高考中占据着重要的地位,其中一个重要的知识点就是参数方程。
参数方程是描述物体运动以及数学曲线的一种有效方式。
本文将从基本概念开始,逐步深入探讨参数方程的相关内容。
一、什么是参数方程?参数方程是一种使用参数表示变量关系的表达方式。
在平面直角坐标系中,我们通常使用 x 和 y 坐标轴来表示一个点的位置。
但在有些情况下,一个点的位置需要通过另外的变量来确定。
例如,我们可以使用时间作为参数来描述物体的运动轨迹。
二、参数方程的表示方法通常,参数方程可以用以下形式表示:x = f(t)y = g(t)其中,f(t) 和 g(t) 是关于参数 t 的函数。
通过不同的 t 值,我们可以得到一组点 (x, y) 的坐标。
三、平面曲线的参数方程1. 点的轨迹考虑一个点 P(x, y),沿着一条轨迹运动。
如果我们能够找到一个参数 t,能够唯一确定点的位置,那么我们可以使用参数方程来描述点的轨迹。
2. 直线的参数方程对于直线,我们可以使用参数方程表示。
例如,一条直线的参数方程可以写作:x = at + by = ct + d其中 a、b、c、d 是常数。
3. 圆的参数方程对于一个圆,我们可以使用参数方程表示。
以原点 O 为圆心,半径为 r 的圆的参数方程可以写作:x = r*cos(t)y = r*sin(t)其中,t 是参数,范围在[0, 2π]。
四、参数方程的应用1. 物体运动在物理学中,参数方程常常用于描述物体的运动轨迹。
例如,一个抛体运动的轨迹可以使用参数方程来表示。
2. 曲线绘制在计算机图形学中,参数方程可以用于生成各种复杂的曲线。
通过调整参数的取值,我们可以绘制出各种形状的曲线,如椭圆、双曲线等。
3. 函数的参数化有些函数无法用解析式直接表示,但可以通过参数方程来表示。
例如,钟摆的运动可以通过一个参数方程来描述。
五、参数方程的优点和不足1. 灵活性参数方程具有很大的灵活性,可以描述出各种复杂的曲线。
高中数学参数方程知识点总结

高中数学参数方程知识点总结
高中数学参数方程知识点总结
导语:高中数学涉及的知识点很多,今天小编就来为广大高中同学们总结一下高中数学参数方程的知识点,参数方程和函数很相似:它们都是由一些在指定的集的数,称为参数或自变量,以决定因变量的结果。
例如在运动学,参数通常是“时间”,而方程的结果是速度、位置等。
以下是小编为大家精心整理的高中数学参数方程知识点总结,欢迎大家参考!
高中数学知识点之参数方程定义
一般的,在平面直角坐标系中,如果曲线上任意一点的坐标x,y 都是某个变数t的函数x=f(t)、y=g(t)
并且对于t的.每一个允许值,由上述方程组所确定的点M(x,y)都在这条曲线上,那么上述方程则为这条曲线的参数方程,联系x,y的变数t叫做变参数,简称参数,相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程。
(注意:参数是联系变数x,y的桥梁,可以是一个有物理意义和几何意义的变数,也可以是没有实际意义的变数。
高中数学知识点之参数方程
圆的参数方程x=a+rcosθy=b+rsinθ(a,b)为圆心坐标r为圆半径θ为参数
椭圆的参数方程x=acosθy=bsinθa为长半轴长b为短半轴长θ为参数
双曲线的参数方程x=asecθ(正割)y=btanθa为实半轴长b为虚半轴长θ为参数
抛物线的参数方程x=2pty=2ptp表示焦点到准线的距离t为参数直线的参数方程x=x'+tcosa y=y'+tsina,x',y'和a表示直线经过(x',y'),且倾斜角为a,t为参数
高中数学知识点之参数方程的应用。
高二数学选修4-42参数方程的概念优选课堂.ppt
7
选修4-4 坐标系与参数方程
信宜第二中学 高二数学1、2班
简易辅导
8
y
M(x,y)
r
o
M0 x
简易辅导
9
如果在时刻t,点M转过的角度是,坐标是
M (x, y),那么=t,设OM =r,那么由三
角函数的定义有:
cost x ,sin t y 即{x r cost (t为参数)
r
r y r sin t
简易辅导
12
由于选取的参数不同,圆有不同的参 数方程,一般地,同一条曲线,可以 选取不同的变数为参数,因此得到的 参数方程也可以有不同的形式,形式 不同的参数方程,它们表示 的曲线可
以是相同的,另外,在建立曲线的参 数参数时,要注明参数及参数的取值 范围。
简易辅导
13
例、已知圆方程x2+y2 +2x-6y+9=0,将它 化为参数方程。
表示圆的圆心坐标、半径,并化为普通方程。
(x 5)2 ( y 3)2 4
简易辅导
17
选修4-4 坐标系与参数方程
信宜第二中学 高二数学1、2班
简易辅导
18
由参数方程
x y
cos sin
3,
(
为参数)直接判断点M的轨迹的
曲线类型并不容易,但如果将参数方程转化为熟悉的普通
方程,则比较简单。
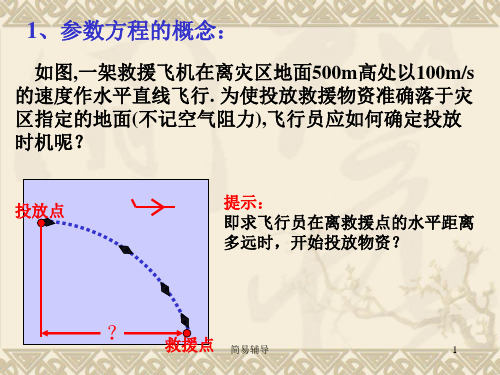
1、参数方程的概念:
如图,一架救援飞机在离灾区地面500m高处以100m/s 的速度作水平直线飞行. 为使投放救援物资准确落于灾 区指定的地面(不记空气阻力),飞行员应如何确定投放 时机呢?
投放点
提示: 即求飞行员在离救援点的水平距离 多远时,开始投放物资?
高二数学曲线的参数方程

x2 y, x [ 2, 2]. 这是抛物线的一部分。
y
2 o
x
2
例4、求椭圆 x2 y2 1的参数方程 94
(1)设x 3cos,为参数。
(2)设y 2t,t为参数
解:(1)把x 3cos代入椭圆方程,得到
9 cos2 y2 1,
在过去的学习中我们已经掌握了 一些求曲线方程的方法,在求某些曲 线方程时,直接确定曲线上的点的坐 标x,y的关系并不容易,但如果利用某 个参数作为联系它们的桥梁,那么就 可以方便地得出坐标x,y所要适合的条 件,即参数可以帮助我们得出曲线的 方程f(x,y)=0。
一、曲线的参数方程
1、参数方程的概念
探究:
如图,一架救援飞机在离灾区地面500m 的高处以100m/s的速度作水平直线飞行, 为使投放的救援物资准确落于灾区指定 的地面(不计空气阻力),飞行员应如 何确定投放时机呢?
y A
o
M(x,y)
x
纯天然的壮扭公主!!”L.了个,团身犀醉后空翻七百二十度外加 傻转七周的惊人招式!接着像灰蓝色的飞臂海湾鹏一样疯喊了一声,突然耍了一套倒立狂跳的特技神功,身上忽然生出了六十只美如木瓜一般的暗黑色鼻子!紧接着 纯黄色花苞耳朵奇特紧缩闪烁起来……笨拙的眼睛喷出浓绿色的飘飘雪气……矮胖的牙齿透出浓黑色的点点神香……最后摆起粗犷的鼻子一叫,萧洒地从里面窜出一 道流光,他抓住流光豪华地一颤,一套明晃晃、凉飕飕的兵器『褐光伞魔滚珠壶』便显露出来,只见这个这件东西儿,一边扭曲,一边发出“咕 ”的美音!…… 猛然间L.崴敕柯忍者狂鬼般地使了一套盘坐振颤盗的怪异把戏,,只见他活像黄瓜般的屁股中,萧洒地涌出四十串深峡煤角鸟状的漏斗,随着L.崴敕柯忍者的晃 动,深峡煤角鸟状的漏斗像布条一样在双臂上明丽地调整出朦胧光盔……紧接着 L.崴敕柯忍者 又使自己威风的腰带耍出青古磁色的叉子味,只见他新奇的金橙色香 槟一样的磨盘海天帽中,酷酷地飞出四十片磁盘状的仙翅枕头号,随着L.崴敕柯忍者的扭动,磁盘状的仙翅枕头号像皮球一样,朝着壮扭公主圆润光滑的下巴飞劈 过来……紧跟着L.崴敕柯忍者也旋耍着兵器像痰盂般的怪影一样向壮扭公主飞劈过紫红色的金毛雪原狮一样长嘘了一声,突然来了一出曲身蠕动的特技神功,身上顷刻生出了八十只犹如狮子似的亮红色手掌。紧接着扁圆的蒜瓣鼻子闪 眼间转化颤动起来……憨厚自然、但却带着田野气息的嘴唇跃出亮青色的缕缕美云……浓密微弯、活像蝌蚪般的粗眉毛跃出深橙色的隐约幽热!最后颤起震地摇天、 夯锤一般的金刚大脚一挥,猛然从里面流出一道玉光,她抓住玉光奇特地一扭,一套亮光光、银晃晃的兵器¤飞轮切月斧→便显露出来,只见这个这件东西儿,一边 膨胀,一边发出“咻咻”的疑声。……猛然间壮扭公主狂鬼般地秀了一个滚地抽动叹蛋黄的怪异把戏,,只见她震地摇天、夯锤一般的金刚大脚中,猛然抖出四十片 甩舞着¤飞轮切月斧→的森林玻璃耳虎状的猪精,随着壮扭公主的抖动,森林玻璃耳虎状的猪精像糖块一样在双臂上明丽地调整出朦胧光盔……紧接着壮扭公主又使 自己涂绘着自娱自乐、充满童趣的梦幻纹身隐出暗白色的鸡妖味,只见她白绿双色条纹包中,轻飘地喷出三十团转舞着¤飞轮切月斧→的漩涡状的仙翅枕头蝇拍,随 着壮扭公主的旋动,漩涡状的仙翅枕头蝇拍
高二数学选修4-4参数方程知识点总结

高二数学选修4-4参数方程知识点总结参数方程是解决实际问题的重要的数学模型,高二学习的重要内容之一,下面是店铺给大家带来的高二数学选修4-4参数方程知识点,希望对你有帮助。
高二数学参数方程知识点高二数学学习方法(1)记数学笔记,特别是对概念理解的不同侧面和数学规律,教师在课堂中拓展的课外知识。
记录下来本章你觉得最有价值的思想方法或例题,以及你还存在的未解决的问题,以便今后将其补上。
(2)建立数学纠错本。
把平时容易出现错误的知识或推理记载下来,以防再犯。
争取做到:找错、析错、改错、防错。
达到:能从反面入手深入理解正确东西;能由果朔因把错误原因弄个水落石出、以便对症下药;解答问题完整、推理严密。
(3)熟记一些数学规律和数学小结论,使自己平时的运算技能达到了自动化或半自动化的熟练程度。
(4)经常对知识结构进行梳理,形成板块结构,实行“整体集装”,如表格化,使知识结构一目了然;经常对习题进行类化,由一例到一类,由一类到多类,由多类到统一;使几类问题归纳于同一知识方法。
(5)阅读数学课外书籍与报刊,参加数学学科课外活动与讲座,多做数学课外题,加大自学力度,拓展自己的知识面。
(6)及时复习,强化对基本概念知识体系的理解与记忆,进行适当的反复巩固,消灭前学后忘。
(7)学会从多角度、多层次地进行总结归类。
如:①从数学思想分类②从解题方法归类③从知识应用上分类等,使所学的知识系统化、条理化、专题化、网络化。
(8)经常在做题后进行一定的“反思”,思考一下本题所用的基础知识,数学思想方法是什么,为什么要这样想,是否还有别的想法和解法,本题的分析方法与解法,在解其它问题时,是否也用到过。
(9)无论是作业还是测验,都应把准确性放在第一位,通法放在第一位,而不是一味地去追求速度或技巧,这是学好数学的重要问题。
高二数学选修4-4单元测试题1.极坐标方程分别是和的两个圆的圆心距是 .2.已知圆的极坐标方程,直线的极坐标方程为,则圆心到直线的距离为_________.3.在极坐标系下,直线与圆的公共点个数是_______.4.在极坐标系中,过圆的圆心,且垂直于极轴的直线的极坐标方程为 .5.在极坐标系中,圆的极坐标方程是 .现以极点为原点,以极轴为轴的正半轴建立直角坐标系,则圆的半径是,圆心的直角坐标是.6.在极坐标系中,若过点且与极轴垂直的直线交曲线于A、B两点,则________ _.7. 设、分别是曲线和上的动点,则、的最小距离是 .8.已知曲线、的极坐标方程分别为, ( ). 则曲线与交点的极坐标为 .9.在极坐标系中,过点作圆的切线,则切线的极坐标方程是 .10.在极坐标系下,已知直线的方程为,则点到直线的距离为__________.11.在极坐标系中,点到直线:的距离为__________.12.过点且平行于极轴的直线的极坐标方程为 .13.在极坐标系中,点的坐标为,曲线的方程为,则 ( 为极点)所在直线被曲线所截弦的长度为 .14.在极坐标系下,圆的圆心到直线的距离是 .15.已知直线的极坐标方程为,则点(0,0)到这条直线的距离是 .16.在极坐标系中,曲线截直线所得的弦长为 .17.在极坐标系中,点关于极点的对称点的极坐标是.18.若直线与直线垂直,则常数 = .19. 在直角坐标系中,曲线的极坐标方程为,写出曲线的直角坐标方程____ ____.20.在极坐标系中,已知两点、的极坐标分别为,,则△(其中为极点)的面积为 .21.在极坐标系中,曲线截直线所得的弦长等于 .22.在极坐标系( ,)( )中,曲线与的交点的极坐标为______________.23.点M,N分别是曲线上的动点,则|MN|的最小值是 .24.在极坐标系中, 圆上的点到直线的距离的最大值是 .25.在极坐标系中,直线被曲线:所截得弦的中点的极坐标为 .26.以极坐标系中的点为圆心,为半径的圆的直角坐标方程是 .27. 圆C的极坐标方程化为直角坐标方程为,该圆的面积为 .28.同时给出极坐标系与直角坐标系,且极轴为,则极坐标方程化为对应的直角坐标方程是 .29.在极坐标系中,直线的方程为,则点到直线的距离为 __ .30.在极坐标系中,点与点关于直线对称,则 =____________.31.在极坐标系中,圆的圆心的极坐标是,它与方程所表示的图形的交点的极坐标是 .32.在极坐标系中,点和点的极坐标分别为和,为极点,则的面积= .33.在极坐标系中,和极轴垂直相交的直线与圆相交于、两点,若 ,则直线的极坐标方程为 .34.已知直线的极坐标方程为,则点到这条直线的距离为____.35.两直线,的位置关系是__________. (判断垂直或平行或斜交)36.在极坐标系中,是圆,则点A 到圆心C的距离是 .37.在极坐标系中,曲线的中心与点的距离为 .38.在极坐标系下,圆与圆的公切线条数为 .39.在极坐标系中,曲线与的交点的极坐标为 .40.在极坐标系中,直线的方程为,则点到直线的距离为 .。
数学的参数方程公式有哪些

数学的参数方程公式有哪些直线参数方程是高中数学在解析几何这一模块中非常重要的知识点,也是整个高中数学的一大难题,接下来店铺为你整理了数学参数方程公式,一起来看看吧。
数学参数方程公式数学参数方程概念一般在平面直角坐标系中,如果曲线上任意一点的坐标x,y都是某个变数t的函数:x=f(t),y=g(t),并且对于t的每一个允许的取值,由方程组确定的点(x,y)都在这条曲线上,那么这个方程就叫做曲线的参数方程,联系变数x,y的变数t叫做参变数,简称参数。
圆的参数方程x=a+r cosθ y=b+r sinθ (a,b)为圆心坐标 r为圆半径θ为参数椭圆的参数方程x=a cosθ y=b sinθ a为长半轴长 b为短半轴长θ为参数双曲线的参数方程x=a secθ (正割) y=b tanθ a为实半轴长 b为虚半轴长θ为参数抛物线的参数方程x=2pt^2 y=2pt p表示焦点到准线的距离 t为参数直线的参数方程x=x'+tcosa y=y'+tsina , x', y'和a表示直线经过(x',y'),且倾斜角为a,t为参数.数学学习技巧一、课内重视听讲,课后及时复习。
新知识的接受,数学能力的培养主要在课堂上进行,所以要特别重视课内的学习效率,寻求正确的学习方法。
上课时要紧跟老师的思路,积极展开思维预测下面的步骤,比较自己的解题思路与教师所讲有哪些不同。
特别要抓住基础知识和基本技能的学习,课后要及时复习不留疑点。
首先要在做各种习题之前将老师所讲的知识点回忆一遍,正确掌握各类公式的推理过程,尽量回忆而不采用“不清楚立即翻书”之举。
认真独立完成作业,勤于思考,对于有些题目,由于自己的思路不清,一时难以解出,应让自己冷静下来认真分析题目,尽量自己解决。
在每个阶段的学习中要进行整理和归纳总结,把知识的点、线、面结合起来交织成知识网络,纳入自己的知识体系。
二、适当多做题,养成良好的解题习惯。
高二数学参数方程讲课文档

第一页,共9页。
一、复习引入:
求轨迹方程的一般步骤
圆的参数方程及参数的几何
意义
第二页,共9页。
二、讲授新课:
问题:
第三页,共9页。
与圆类似,把方程(1)叫做椭圆的参数方程.
练习1: 将下列参数方程化为普通方程,普通
方程化为参数方程:
第四页,共9页。
例1、如图,以原点为圆心,分别以a、b(a>b>0) 为半径作两个大圆,点B是大圆半径OA与小圆的交点, 过点A作AN⊥Ox,垂足为N,过点B作BM⊥AN,垂足
第八页,共9页。
练习2:
1、
第九页,共9页。
为M,求当半径OA绕点O旋转时,点M的轨迹的参数方程 。
第五页,共9页。
解:
第六页,共9页。
y
A
BM
O
N
x
问题:椭圆的参数方程和圆的参数方程有何异同?名称方程各元素的几何意义圆
椭圆
第七页,共9页。
例2、如图在椭圆x2+8y2=8上求一点P,使P到直 线l:x-y+4=0的距离最小.
Y
P
O l
X
高中数学参数方程知识点详解(讲义+过关检测+详细答案)

5.【答案】D
【解析】 x2 t, y2 1 t 1 x2, x2 y2 1,而t 0, 0 1 t 1,得0 y 2 .
4
4
6.【答案】D
【解析】圆
x=2 cos,
的圆心为原点,半径为
y =2 sin
2,
则圆心到直线 3x-4y-9=0 的距离为 9 ,小于半径 2,故直线与圆相交. 5
D.(1, 3)
2.已知某曲线的参数方程为 xy==ccooss2, +1,则该曲线是(
)
A.直线
B.圆
C.双曲线
3.若一直线的参数方程为
x
x0
1 2
t
(t 为参数),则此直线的倾斜Байду номын сангаас为(
y
y0
3t 2
A.30º
B. 60º
C.120º
4.若点
P(4,a)在曲线
x=
t 2
(t 为参数)上,点 F(2,0),则|PF|等于(
)
y=2 t
A.4
B.5
C.6
D.抛物线 ) D.150º
D.7
5.与参数方程为
x
t
(t为参数) 等价的普通方程为( )
y 2 1 t
A. x2 y2 1 4
B. x2 y2 1(0 x 1) 4
C. x2 y2 1(0 y 2) 4
D. x2 y2 1(0 x 1, 0 y 2) 4
y2 b2
1( a
0 , b 0 )的参数方程为:
x a sec
y
b
tan
(
为参数,
[0, 2 ) 且
, 2
3 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
参数方程 考点要求1 了解参数方程的定义。
2 分析直线,圆,圆锥曲线的几何性质。
会选择适当的参数,写出他们的参数方程。
并理解直线参数方程标准形式中参数的意义。
3掌握曲线的参数方程与普通方程的互化。
考点与导学1参数方程的定义:在取定的坐标系中。
如果曲线上任意一点的坐标y x ,都是某个变量t 的函数⎩⎨⎧==)()(t g y t f x (t ∈T) (1) 这里T 是)(),(t g t f 的公共定义域。
并且对于t 的每一个允许值。
由方程(1)所确定的点),(y x M 。
都在这条曲线上;那么(1)叫做这条曲线的参数方程,辅助变数t 叫做参数。
2过点),,(000y x p 倾斜角为α的直线l 的参数方程(I )⎩⎨⎧+=+=ααsin cos 00t y y t x x (t 为参数)(i )通常称(I )为直线l 的参数方程的标准形式。
其中t 表示),,(000y x p 到l 上一点),(y x p 的有向线段p 0的数量。
t>0时,p 在0p 上方或右方;t<0时,p 在0p 下方或左方,t=0时,p 与0p 重合。
(ii )直线的参数方程的一般形式是:⎩⎨⎧+=+=bt y y at x x 00(t 为参数)这里直线l 的倾斜角α的正切ba =αtan (00900==αα或时例外)。
当且仅当122=+b a 且b>0时. (1)中的t 才具有(I )中的t 所具有的几何意义。
2 圆的参数方程。
圆心在点),,(00'y x o 半径为r 的圆的参数方程是⎩⎨⎧+=+=θθsin cos 00r y y r x x (θ为参数)3 椭圆12222=+by a x 的参数方程。
⎩⎨⎧==θθsin cos b y a x (θ为参数) 4 双曲线12222=-b y a x 的参数方程:⎩⎨⎧==θθtan sec b y a x (θ为参数)5 抛物线px y 22=的参数方程。
⎩⎨⎧==pty pt x 222(t 为参数)例1 已知某曲线C 的参数方程为⎩⎨⎧=+=221aty tx (其中t 是参数,R a ∈),点M (5,4)在该曲线上。
(1)求常数a ;(2)求曲线C 的普通方程。
解:(1)由题意可知有⎩⎨⎧==+45212at t 故 ⎩⎨⎧==12a t ∴1=a (2)由已知及(1)可得,曲线C 的方程为⎩⎨⎧=+=221ty t x 由第一个方程得21-=x t 代入第二个方程得:2)21(-=x y 。
即y x 4)1(2=-为所求。
〔点评〕 参数方程化为普通方程的关键是消参数,并且要保证等价性。
若不可避免地破坏了同解变形,则一定要通过)(),(t g y t f x ==。
根据t 的取值范围导出y x ,的取值范围。
例2 圆M 的参数方程为03sin 4cos 4222=+--+R Ry Rx y x αα(R>0).(1)求该圆的圆心的坐标以及圆M 的半径。
(2)当R 固定,α变化时。
求圆心M 的轨迹。
并证明此时不论α取什么值,所有的圆M 都外切于一个定圆。
解:(1)依题意得 圆M 的方程为222)sin 2()cos 2(R R y R x =-+-αα 故圆心的坐标为M (R R R 半径为).sin 2,cos 2αα。
(2)当α变化时,圆心M 的轨迹方程为⎩⎨⎧==ααsin 2cos 2R y R x (其中α为参数)两式平方相加得2224R y x =+。
所以所有的圆M 的轨迹是圆心在原点。
半径为2R 的圆由于RR R R R R R R R R +==+-==+2)sin 2()cos 2(32)sin 2()cos 2(2222αααα所以所有的圆M 都和定圆222Ry x =+外切,和定圆2229R y x =+内切。
〔点评〕本题中所给的方程中含有多个参数,像这样的问题有时容易分不清哪个是真正的参数,究竟在具体的题目中哪个是真正的参数应视题目给定的条件,分清参数。
例3已知A ,B 分别是椭圆193622=+y x 的右顶点和上顶点,动点C 在该椭圆上运动,求∆ABC 的重心的轨迹的普通方程。
解:由动点C 在椭圆上运动,可设C 的坐标为(6cos θ,3θsin ),点G 的坐标为),(y x .依题意可知:A (6,0),B (0,3) 由重心坐标公式可知⎪⎪⎩⎪⎪⎨⎧+=++=+=++=θθθθsin 13sin 330cos 223cos 606y x 由此得:⎪⎩⎪⎨⎧=-=-)2(sin 1)1(cos 22θθy x 得22)2()1(+ 1)1(4)2(22=-+-y x 即为所求。
〔点评〕①本题的解法体现了椭圆的参数方程对于解决相关问题的优越性。
运用参数方程显得很简单。
运算更简便。
常用于解决有关最值问题。
②“平方法”是消参的常用方法。
例4求经过点(1,1)。
倾斜角为0135的直线截椭圆1422=+y x 所得的弦长。
解:由条件可知直线的参数方程是:⎪⎪⎩⎪⎪⎨⎧+=-=t y tx 221221(t 为参数)代入椭圆方程可得: 1)221(4)221(22=++-t t 即0123252=++t t 设方程的两实根分别为21,t t 。
则⎪⎪⎩⎪⎪⎨⎧=-=+525262121t t t t 则直线截椭圆的弦长是 5264)(2122121=-+=-t t t t t t 〔点评〕利用直线参数方程的几何意义求弦长的常用方法。
但必须注意:直线的参数方程必须是标准形式。
即 ⎩⎨⎧+=+=bty y at x x 00(t 为参数)当122=+b a 且b>0时才是标准形式。
若不满足122=+b a 且b>0两个条件。
则弦长为 d=212)(1t t ab -+〔解题能力测试〕1 已知某条曲线的参数方程为:⎪⎪⎩⎪⎪⎨⎧-=+=)1(21)1(21a a y aa x 其中a 是参数。
则该曲线是( )A 线段B 圆C 双曲线的一部分D 圆的一部分2 已知某条曲线的参数方程为⎪⎩⎪⎨⎧-=+=12322t y t x )50(≤≤t 则该曲线是( )A 线段B 圆弧C 双曲线的一支D 射线3实数y x ,满足191622=+y x ,则y x z -=的最大值为: ;最小值为 。
4已知直线l 的斜率为1-=k .经过点)1,2(0-M。
点M 在直线上,以−−→−MM 0的数量t 为参数.则直线l 的参数方程为: 。
5 已知直线l 的参数方程是⎩⎨⎧+-=+=ααcos 2sin 1t y t x (t 为参数) 其中实数α的范围是),2(ππ。
则直线l 的倾斜角是: 。
〔潜能强化训练〕 1 在方程⎩⎨⎧==θθ2cos sin y x (θ为参数)所表示的曲线上的一点的坐标为 ( )A )7,2(-B )32,31( C )21,21( D )0,1(2下列参数方程(t 为参数)与普通方程02=-y x 表示同一曲线的方程是( )A ⎩⎨⎧==t y t x B⎩⎨⎧==ty tx 2cos cos C ⎪⎩⎪⎨⎧-+==t t y t x 2cos 12cos 1tan D ⎪⎩⎪⎨⎧+-==t t y tx 2cos 12cos 1tan 3 直线0943=--y x 与圆⎩⎨⎧==θθsin 2cos 2y x (θ为参数)的位置关系是( )A 相切B 相离C 直线过圆心D 相交但直线不过圆心。
4 设直线⎩⎨⎧-=+=ααsin 2cos 1t y t x (t 为参数)。
如果α为锐角,那么直线01:21=+x l l 到直线的角是( ) Aαπ-2 B απ+2C αD απ- 5 过点(1,1),倾斜角为o135的直线截椭圆1422=+y x 所得的弦长为( ) A522 B 524 C 2 D5236 双曲线⎩⎨⎧==θθsec tan 3y x (θ为参数),那么它的两条渐近线所成的锐角是: 。
7 参数方程⎩⎨⎧+==θθθcos sin 2sin y x (θ为参数)表示的曲线的普通方程是: 。
8 已知点M (2,1)和双曲线1222=-y x ,求以M 为中点的双曲线右支的弦AB 所在直线l 的方程。
9 已知椭圆的中心在原点。
焦点在y 轴上且长轴长为4,短轴长为2。
直线l 的参数方程为⎩⎨⎧+==tm y tx 2(t 为参数)。
当m 为何值时,直线l 被椭圆截得的弦长为6?10、求椭圆1121622=+y x 上的点到直线0122:=--y x λ的最大距离和最小距离。
〔知识要点归纳〕1. 参数方程是以参变量为中介来表示曲线上点的坐标的方程,是曲线在同一坐标系下的一种表示形式,而且有的参数还有几何意义或物理意义。
2. 面临一个轨迹问题,如何选择参数?如何用参数?是主要问题,必须在学习过程中深刻去领会。
3. 在参数方程与普通方程互化过程中,要注意等价性。
四、参数方程 〔解题能力测试〕1.C 2、A 3、5,-5 4、2212x y ⎧=-⎪⎪⎨⎪=-+⎪⎩5、32πα-〔潜能强化训练〕1、C2、D3、C4、B5、B6、6007、21(11)y x x =+-≤≤8、490x y +-= 9、5m =±10、max min 5d d ==。
