晶粒大小、点阵畸变、宏观应力DOC
材料科学基础名词解释汇总

组元原子有序排列的固溶体,溶质在晶格完全有序排列。 置换固溶体
当溶质原子溶入溶剂中形成固溶体时,溶质原子占据溶剂点阵的阵点,或者说溶质原子置换了溶剂点 阵的部分溶剂原子,这种固溶体就称为置换固溶体。 间隙固溶体
溶质原子分布于溶剂晶格间隙而形成的固溶体称为间隙固溶体。 有限固溶体
溶质在固溶体中的溶解度有一定限度,这种固溶体称为有限固溶体。 无限固溶体(连续固溶体)
位错线沿着滑移面的运动称为位错的滑移。 滑移系
晶体中一个滑移面及该面上一个滑移方向的组合称一个滑移系。 交滑移
当某一螺型位错在原滑移面上运动受阻时,有可能从原滑移面转移到与之相交的另一滑移面上去继续 滑移,这一过程称为交滑移。 双交滑移
如果交滑移后的位错再转回和原滑移面平行的滑移面上继续运动,则称为双交滑移。 多滑移
电子化合物是指由主要电子浓度决定其晶体结构的一类化合物,又称休姆-罗塞里相。凡具有相同的电 子浓度,则相的晶体结构类型相同。 大角度晶界
多晶材料中各晶粒之间的晶界称为大角度晶界,即相邻晶粒的位相差大于10º的晶界。 小角度晶界
相邻亚晶粒之间的位相差小于10º,这种亚晶粒间的晶界称为小角度晶界,一般小于2º,可分为倾斜 晶界、扭转晶界、重合晶界等。 固溶强化
两组元A和B组成合金时,除了形成以A为基或以B为基的固溶体外,还可能形成晶体结构与A,B两组 元均不相同的新相。由于它们在二元相图上的位置总是位于中间,故通常把这些相称为中间相。 配位数
晶体结构中任一原子周围最近邻且等距离的原子数。 致密度
晶体结构中原子体积占总体积的百分数。 金属键
自由电子与原子核之间静电作用产生的键合力。 共价键
X射线测定材料晶粒大小与晶格畸变率

B0/B1==>β/B1==>β
(三)晶粒大小和晶格畸变的同时测定
۞X射线宽化构成
X射线 衍射峰宽化
几何 宽化
物理 宽化
晶粒细化 宽化
点阵畸变 宽化
۞由物理宽化因素造成的强度分布曲线称为
本质曲线,记作: I g(,x其) 积分宽度为:
II b
( x)dx
g
g ( x)dx
g .m
۞由几何宽化因素造成的强度分布曲线称为
۞“晶粒细化”与”晶格畸变”两种效应的叠加, 亦遵循x)
M(x),N(x)分别为”晶粒细化”和”显微畸变”宽 化函数,其相应积分宽度为βD,βε. β为总的本质曲线 积分宽度.
采用近似函数法求解晶粒尺寸与显微畸变
基本步骤: 进行Kα1和Kα2双重线的分离,得到纯Kα1线形. 选择几何宽化和物理宽化的近似函数类型. 进行几何宽化效应和物理宽化效应的分离,得总物
在地质和考古学中,有人论证古脊椎动物牙齿 中磷灰石晶粒大小与化石本身地质年代相关联.
在多相催化领域中,晶格不规整性可直接关联到表 面催化的活性中心:
1 在表面点缺陷和显现位错处,催化剂原子几何排布与 表面其它地方不同,易产生催化活性中心. 2 与位错和缺陷相联系的表面点,能够产生固体电子性 能的修饰,所以晶格不规整处有更高催化活性.
晶体在其整个范围内,原子全部精确的定位于无畸变 的空间点阵的阵点上.
2 完整性的内容
晶格完整性应该是晶体结构中结点上原子或离子规则 排列的延续状况的描述.这种状况不仅包括晶体内部是 否存在空缺、位错、扭曲,而且还包括在三维空间的 延续距离的大小.
3 衍射谱线加宽
➢ 对于无畸变、足够大的晶粒组成的多晶试样,经过 理论推算,其粉末试样的谱线应该特别尖锐,宽度以 秒度量.
实验七 晶体晶粒大小和晶格畸变的测定

实验七晶体晶粒大小和晶格畸变的测定一、实验目的与要求1.学习用X射线衍射峰宽化测定微晶大小与晶格畸变的原理和方法。
2.掌握使用X射线衍射分析软件进行晶粒大小和晶格畸变测定。
二、实验原理X射线衍射峰的宽化主要有三个因素造成的:仪器宽化(本征宽化),晶块细化和微观应变。
要计算晶粒尺寸或微观应变,首先第一步应当从测量的宽度中扣除仪器的宽度,得到晶粒细化或微观应变引起的真实加宽。
但是,这种线形加宽效应不是简单的机械叠加,而是它们形成的卷积。
所以,我们得到一个样品的衍射谱以后,首先要做的是从中解卷积,得到样品因为晶粒细化或微观应变引起的加宽FW(S)。
这个解卷积的过程非常复杂,解卷积的过程,Jade按下列公式进行计算。
式中D称为反卷积参数,可以定义为1-2之间的值。
一般情况下,衍射峰图形可以用柯西函数或高斯函数来表示,或者是它们二者的混合函数。
如果峰形更接近于高斯函数,设为2,如果更接近于柯西函数,则取D=1。
另外,当半高宽用积分宽度代替时,则应取D值为1。
D的取值大小影响实验结果的单值,但不影响系列样品的规律性。
因为晶粒细化和微观应变都产生相同的结果,那么我们必须分三种情况来说明如何分析。
(1)如果样品为退火粉末,则无应变存在,衍射线的宽化完全由晶粒比常规样品的小而产生。
这时可用谢乐方程来计算晶粒的大小。
式中Size表示晶块尺寸(nm),K为常数,一般取K=1,λ是X射线的波长(nm),FW(S)是试样宽化(Rad),θ则是衍射角(Rad)。
计算晶块尺寸时,一般采用低角度的衍射线,如果晶块尺寸较大,可用较高衍射角的衍射线来代替。
晶粒尺寸在30nm左右时,计算结果较为准确,此式适用范围为1-100nm。
超过100nm的晶块尺寸不能使用此式来计算,可以通过其它的照相方法计算。
(2)如果样品为合金块状样品,本来结晶完整,而且加工过程中无破碎,则线形的宽化完全由微观应变引起。
式中Strain表示微观应变,它是应变量对面间距的比值,用百分数表示。
x射线衍射分析应用的晶格常数

第十三页,共85页。
体心立方
体心立方中,H+K+L为奇数的衍射面不出现,因此,比值数列应可化
成:
Si2 n1:Si2 n2: 1:2:3:4:5:6:7:8:
心立方中,第二条线比第一条线弱。
第二十页,共85页。
在实际测量时,某一条或几条衍射强度特别低的线条可能不会出现, 可能导致判断错误。如数列为3:8:11:16:19,肯定不是简单立方, 也不属于体心立方(数列中有奇有偶),因此,应为面心立方结构, 但在实际测量时,没有出现4(200)、12(222)。因为结构因子 太小。
9 0.0222 0.0980 0.2496
10 0.2013 0.2771 0.4287
第四十一页,共85页。
为了解决六方晶系的指标化问题,有人还绘出了 图解法图表,利用该图表,可直接对六方晶系进 行指标化
进行指标化的样品最好是纯物相,否则因为其它 物相的存在干扰指标化的正常判断
第四十二页,共85页。
衍射谱标定就是要从衍射谱判断出试样所属的晶系、点阵胞 类型、各衍射面指数并计算出点阵参数。
步骤
– 判断试样的晶系 – 判断试样的点阵胞类型 – 确定晶面指数 – 计算点阵常数
第七页,共85页。
衍射谱的指标化是晶体结构分析和点阵常数测定的基础。 1)已知晶系和晶格常数a,从理论上求出,与实验值对比,
第三十八页,共85页。
课堂练习
实验所用辐射为 CuKα= 0.15418nm,下表 给出四个样品的 sin2θ值,请标定出 各组实验数据的衍射 面指数、所属晶系, 布拉菲点阵类型,并 计算出点阵常数。
点阵常数与宏观应力测定

计算结果:M=0.3464, b=98.6930
(4)轴向发散误差:
衍射仪法外推函数:
(1)透明度是主要时,选用cos2:
d A B D 4E cos2 ( 2 C 2 2 ) d sin sin sin sin 2
(2)平板与水平发散是主要时,选用ctg2:
d E ctg 2 ( A B sin C sin 2 D ) 2 d cos
第二类(微观应力)-区域晶面间 距变化为 d,衍射线宽化; 第三类(超微观应力)-原子偏离 平衡位置(若干个原子范围内), 衍射线强度
2. 宏观应力测定的基本原理
样品表面应力与应变状态为平面应力状态:
0, y,z 0, x,z 0
如图所示:表面法线方向为一个主方向,其余两个主方向在 表 面上。 X-ray探测深度有限,简化为平面应力状态。 所以,X-ray探测的是物体表层应力。
4.衍射仪法
衍射仪法不能利用外推函数消除的误差: (1)测角仪机械零点( 2 =0的位置); (2) 2角的2 : 1驱动匹配误差; (3) 计数测量系统滞后(步进法); (4)折射修正;
(5)温度校正。
利用外推函数可消除的误差: (1)平板试样误差: (2)试样表面离轴误差: (3)试样透明度误差:
4.宏观应力测定中的几个问题
峰位的确定:
半高宽法;
抛物线法 应力常数K的确定:
金属材料的微观结构与力学性能

金属材料的微观结构与力学性能金属材料是我们日常生活中经常使用到的一种重要材料,它的力学性能直接决定着其使用价值。
然而,金属材料的微观结构是影响其力学性能的重要因素之一。
因此,了解金属材料的微观结构对于挖掘其潜力具有重要意义。
一、金属材料的组织结构金属材料的组织结构分为三个层次:微观结构、中观结构和宏观结构。
微观结构是由晶体组成的,晶体是由不同的结构单元组成的,包括晶粒、晶界、孪晶等。
中观结构是由晶粒的排列和分布组成的,如晶粒大小、晶粒形状、晶粒取向等。
宏观结构是由各种中观结构构成的,如晶体的尺寸、形状和排列方式等。
晶体是金属材料微观结构的最基本单位,在晶体内部原子是有规律地排列的。
金属材料中晶体是以多面体、圆柱体或板状的形式存在,晶体的大小和形状不同会对金属材料的力学性能产生影响。
晶体的组成通常是由多个原子经过排列形成的,晶体中的原子排列方式和结构不同会影响其力学性能。
此外,晶粒的界面处被称为晶界,晶界的稳定性及其形态对整个材料的力学性能有很大的影响。
二、微观结构对金属材料力学性能的影响1. 晶界影响材料力学性能的强度和韧性,晶界处的塑性变形是材料发生塑性时的一种重要机制,晶界出现裂纹和断裂是材料出现断裂的重要原因之一。
因此,优化金属材料晶界的形态和结构,提高其稳定性,有利于提高材料的整体机械性能。
2. 晶体取向对金属材料力学性能的影响很大。
晶体的取向是指对于某一个方向而言晶体内排列原子的方向性质。
晶体取向的不同会对力学性能产生不同的影响,大多数材料具有各向同性,但某些材料的微观结构有规则地定向排列,称为各向异性。
所有具有各向异性的材料都有一定的单向性质,也就是在某一个方向有更大的强度或韧性。
3. 晶粒的大小和形状对材料的力学性能产生重要影响。
晶粒尺寸大,晶体脆性相对较强,而晶粒尺寸小,其塑性会相对增强。
晶粒形状也会影响晶体的塑性变形,如晶粒呈多面体形状的金属材料相对具有更好的塑性特性。
4. 孪晶结构是一种经常出现在晶体中的微观结构,孪晶结构对于金属材料的塑性行为和断裂行为有重要影响。
第六章--jj--晶粒越大,应力集中越大,晶粒小,应力集中小,在同样外加应力下,小晶粒需要在较大
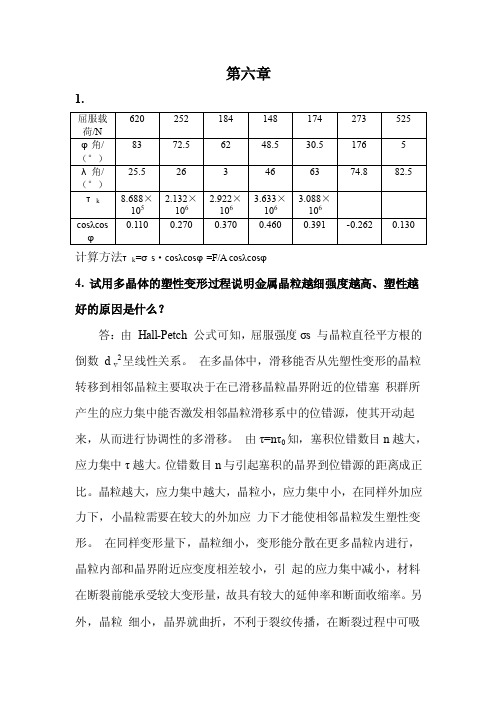
第六章1.计算方法τk=σs·cosλcosυ=F/A cosλcosυ4. 试用多晶体的塑性变形过程说明金属晶粒越细强度越高、塑性越好的原因是什么?答:由Hall-Petch 公式可知,屈服强度σs 与晶粒直径平方根的倒数d v2呈线性关系。
在多晶体中,滑移能否从先塑性变形的晶粒转移到相邻晶粒主要取决于在已滑移晶粒晶界附近的位错塞积群所产生的应力集中能否激发相邻晶粒滑移系中的位错源,使其开动起来,从而进行协调性的多滑移。
由τ=nτ0知,塞积位错数目n越大,应力集中τ越大。
位错数目n与引起塞积的晶界到位错源的距离成正比。
晶粒越大,应力集中越大,晶粒小,应力集中小,在同样外加应力下,小晶粒需要在较大的外加应力下才能使相邻晶粒发生塑性变形。
在同样变形量下,晶粒细小,变形能分散在更多晶粒内进行,晶粒内部和晶界附近应变度相差较小,引起的应力集中减小,材料在断裂前能承受较大变形量,故具有较大的延伸率和断面收缩率。
另外,晶粒细小,晶界就曲折,不利于裂纹传播,在断裂过程中可吸收更多能量,表现出较高的韧性。
6.滑移和孪生有何区别,试比较它们在塑性变形过程的作用。
答:区别:1)滑移:一部分晶体沿滑移面相对于另一部分晶体作切变,切变时原子移动的距离是滑移方向原区别:区别子间距的整数倍;孪生:一部分晶体沿孪生面相对于另一部分晶体作切变,切变时原子移动的距离不是孪生方向原子间距的整数倍;2)滑移:滑移面两边晶体的位向不变;孪生:孪生面两边的晶体的位向不同,成镜面对称;3)滑移:滑移所造成的台阶经抛光后,即使再浸蚀也不会重现;孪生:由于孪生改变了晶体取向,因此孪生经抛光和浸蚀后仍能重现;4)滑移:滑移是一种不均匀的切变,它只集中在某些晶面上大量的进行,而各滑移带之间的晶体并未发生滑移;孪生:孪生是一种均匀的切变,即在切变区内与孪生面平行的每一层原子面均相对于其毗邻晶面沿孪生方向位移了一定的距离。
作用:晶体塑性变形过程主要依靠滑移机制来完成的;孪生对塑性变形的贡献比滑移小得多,但孪生改变了部分晶体的空间取向,使原来处于不利取向的滑移系转变为新的有利取向,激发晶体滑移。
晶粒尺寸和微观应力的测定

sin (
2
)
2θ 212
2θ
O*
{HKL}对应 的倒易球
(m a) 2 I1
2
sin ( (
2
2m 12 d cos
2m 12 d cos (m a) 2
)
I max
)2
I1
2
I max
1 2
sin ( (
2
2m 12 d cos
2m 12 d cos
倒易点(HKL)扩展为一 个区域----倒易空间中 的选择反射区
4 3 2 1 N N N N
0
1 N
2 N
3 N
4 N
因为干涉函数主峰宽度与晶胞数目N成反比, 所以选择反射区的形状和大小与晶体的尺寸 成反比。
选择反射区的形状和大小与晶体的尺寸成反比.
当晶粒尺寸比较小时(<100 nm),每个晶面 所对应的倒易阵点由一个几何点扩展为具 有一定体积的倒易体元。
镍膜电阻率温度系数随晶粒尺寸的变化
REF: J. Appl. Phys,75(1994)3632
微观应力或晶格畸变: 材料经强烈塑性变形 后,由于晶粒变形不均匀而引起的在一个或少数 晶粒范围内存在并保持平衡的内应力;或点阵中 一部分原子偏离其平衡位置造成点阵畸变。 此应力在某些局部区域可达到很大数值,致使 工件在不大的外力下产生裂纹,导致断裂。
晶粒细化的存在,使得厄 瓦尔德图解中的倒易球成 Δ(2θ) 为具有一定厚度的面壳层。 当反射球与倒易球相交时, 反射球 得到宽化的衍射线形。
入射线 C 2θ
衍射线线形
2θ
O*
{HKL}对应 的倒易球
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.4.2晶粒大小、点阵畸变、宏观应力宏观内应力测定:1、概念:除内应力是指产生应力各因素不复存在时,(为外力去除相变停止等),由于不均匀的塑性形变或不均匀的相变新改,物体内部依然存在并自身保持平衡的应力。
内应力按其存在分为三类:○1 在宏观范围晶区存在并保持平衡的应力,称宏观应力或第一类应力。
○2 晶粒间存在并保持平衡的应力,称微观应力或第Ⅱ类内应力。
○3 晶粒内的原子间存在并保持平衡的应力称超微观应力或第三类应力。
研究宏观内应力对材料的疲劳强度、静强度、抗蚀性尺寸稳定性等具有重大意义。
测定方法有电阻应变片法、机械拉伸法等,与机电测法相比,X 光法特点:○1 无损测定,○2测的仅弹性应变(不含塑性应变)、机电为两者之各,○3解研究表层nm 区域局部应变和应力梯度,○4精度21mm kg 级。
2、原理:因各类应力造成晶体点阵畸变不同,相应的衍射图含有不同的变化。
测量这些变化即能区分内应力的类型及数值。
若存在宏观内应力,则宏观尺寸必然产生改变。
在弹性范围内,宏观弹性应变的数值可用某一晶面间距的变化来表征,即可用相应衍射峰位的变化来表征。
若存在微观应力,晶粒会产生很大的塑性变型,引起晶粒的晶格歪扭、弯曲使不同晶粒内的同一组晶面间距发生不规侧的变化,从而造成衍射线宽化。
精测峰宽的问题,不论哪一类,都是先测应变、其应变为:θθε∆⋅-=-=∆=ctg d d d d d 00 d 0,d 为晶面在弹性形变前后的晶面间距,θθγδ∆⋅⋅=ctg EzE ——弹性模量,γ——材料泊松比以上公式为单轴应力的基本公式(各向同性均为棒状材料) 宏观内应力测定:3、实用方法:原理的实用方法有实用价值的测定是,测定沿试样二维表面某方向的宏观内应力,如金属材料(板材或陶瓷、微晶玻璃等)表面沿某一给定方向的应力。
如果测定右图中板材上O 点沿ϕ方向所受的应力φσ,则考虑与φσ处在同一平面内且与Z 轴交角为ψ的衍射晶面结线方向的应力φψσ,根据弹性力学理论:()2121Sin E E φψφννεσψσσ+=-+ (1) 且()0000d d d ctg d d ψφψψεθθθ-∆===-- (2)式中 0θ——无应力试样衍射峰位的布拉格角, 4θ——有应力试样衍射峰位的布拉格角()()200121ctg Sin E Eψφννθθθσψσσ+--=-+于是 (3) (1)和(3)表明在σψ方向上的应变是由特定方向上的应力σψ与主应力之和(σ1+σ2)两部分构成,而且当改变衍射晶面法线与试样表面法线之间的夹角ψ时,主应力和(σ1+σ2)对ψ方向的应变贡献恒定不变。
应变量只与sin 2ψ成线性关系。
故公式改写为02(1)Ectg M ϕσθν=-⋅+ (M 为斜率)实际测时,只要测出各个不同ψ角下的2θψ,并以2θψ为纵坐标sin 2ψ为横坐标作直线,求其斜率为M ,则宏观应力若2θ为度计算则:22M Sin θψ∂=∂ ○1可用专用应力测定仪、或在普通衍射仪上装一个试样架应力即能使试样绕衍射仪轴独立转到所需ψ0,且能改变探测器位置以便聚焦。
一般选一组高角度晶面该面在多晶试样中有各种取向,故在不同ψ下都能测到(θ2>140°)。
取40°、15°、30°、45°的情况下测2σψ,故在相应角度下ψ0必须能改变到相应位置,在ψ0下,做有明显的衍射峰,即固定ψ0测定后,当在相应ψ0下看到明显衍射峰时精测峰位求σψ。
○2普通衍射仪不改变任何装置的情况下也可测这时ψ的各咱取值是ψ=00、 ψ>03、ψ<起始角/2~3。
(扫描hkl 的起始角)由于普通衍射仪计数管位置不能在测定中改变位置,ψ角度越大强度损失越厉害,测不到强度,无法精测d 值,故ψ选03、07……且随ψ增大,计数时间增大10°以后无法转动,不能测。
6、晶粒尺寸与点阵畸变的测定多晶物质是由很多个微小单晶组成的,单晶又由很多晶胞组成,这些微小的单晶又称晶粒或微晶。
这些晶粒的大小(或称微晶尺寸)对材料的性能有着很大的影响。
对于由无畸变.足够大的晶粒组成的多晶试样,衍射理论预言,其粉末花样的谱线应特别锋锐。
但在实际实验中,由于许多仪器因素和物理因素的综合影响,使得衍射线形增宽了。
纯的线形形状和宽度是由试样的平均晶粒尺寸或尺寸分布,以及晶体点阵中的主要缺陷所决定的。
因此,对纯衍射线形做适当的分析,原则上可以得到平均晶粒尺寸. 晶粒尺寸的分布,以及点阵性质和尺度等方面的信息。
晶粒尺寸和晶格畸变率是纳米粒子的重要物理参数。
X射线衍射线宽法是同时测定晶粒大小和晶格畸变的最好方法。
对纳米粉体而言,谱线宽化是晶粒细化和晶格畸变共同影响的结果,因此同时测定是一种理想的近似方法。
可以看到,目前在讨论纳米合成材料的晶格畸变特征的一些场合,存在一些简单的计算方法,在这类的简单计算方法中,共同地以单一的衍射数据为基准,或者是先由谢乐公式计算晶粒度,然后将得到的晶粒度代入同时涉及晶粒度和畸变的公式,以求得晶格畸变值,或者使用单纯由微观应力引起的谱线增宽的计算公式来计算晶格畸变值。
近年来,随着纳米材料及薄膜材料研究的深入开展,人们了解到晶粒大小和点阵畸变程度的大小,对材料的性能有重要影响,可以通过控制加工过程中的晶粒大小和点阵畸变程度的大小,来改善材料的性能,因此对材料的加工过程中的晶粒度和点阵畸变的测量,有十分重要的意义。
这也对晶粒大小和晶格畸变的测定的要求越来越高,而各种测试方法和计算方法都各有优劣。
本文就是讨论用积分宽度法即Hall法和计算机程序来同时计算晶粒大小和晶格畸变率,比较了二者的计算结果的准确性,同时讨论了研磨试样时间长短对晶粒大小和晶格畸变的影响。
一、原理:利用X 射线测定晶粒尺寸与点阵畸变是利用X 射线衍射线型的宽化来进行的(一)线形宽化种类。
1.仪器线形与仪器宽度由于X 射线源有一定的大小宽度,接收狭缝,试样吸收、平板试样、垂直发散、调0,使得符合布拉格条件的衍射不只有一个点、一条线对应一个2θ0而是使偏离2θ范围内仍有一定的符合布拉格反射的,但衍射强度逐渐降低的衍射存在,这就形成了一定宽度的衍射峰,这个峰即使无晶粒细化,无点阵畸变仍然存在,称之为仪器线形g(x),对应仪器宽度b 。
2、物理线形f(x)与物理宽化βf物理宽化指晶粒细化或点阵畸变引起的宽化。
3、试样线形(实验线形h(x))的宽度B 包含仪器宽度b 和物理宽度βf ,任何影响线形的因素迭加在一起,根据迭加定律,有卷积关系。
试样线形)(x h 与仪器线形)(x g 和物理线)(x f 之间有卷积关系:⎰∝∝-=dy y x f y g x h )()()(以上式为基础,为了把f(x)解出来,可用各种近似函数法、傅氏分析法、方差法等不同方法.其中的近似函数法是把h(f)、f(x)和g(x)用某种具体的带有待定常数的函数代替,通过h(x)和g(x)与已经获得实验曲线拟合来确定其待定常数具体数值大小.代人方程,来近似地解出f(x)大小. 各种近似函数法简介1.高斯近似函数积分宽度法令h(x)、g(x)均为高斯函数,则f(x)也一定是高斯函数,令 它们各自的积分宽度分别为B 、b 和β,则有 B 2=b 2+β2 (4.38)如果通过实验测量对形变样品和标准样品分别测到衍射线形 h(x)、g(x),经K α1和K α2双线分离后.并计算出它们的积分 宽度B 、b 以及半高宽2w(B)和2w(b),则由式(4.38)可 求出物理宽度β.当仅由畸变或应变所产生的以2θ为标度的积分宽度β(单位为弧度)求得以后,则最大点阵畸变e 可由下式求出max (/)(2)/4(2)cot 4hkl e d d tg eβθθηβθθ=∆===表观应变2.柯西近似函数积分宽度法令h(x)、g(x)均为柯西函数,则f(x)也一定是柯西函数,令它们各自的积分宽度分别为B 、b 和β,则有 B=b+β如果通过实验测量对形变样品和标准样品分别测到衍射线形 h(x)、g(x) 并计算出它们的积分宽度B 、b 以及半高宽2w(B)和2w(b),则由上式可求出物理宽度β.当仅由晶粒碎化所产生的以2θ为标度的积分宽度β(单位为弧度)求得以后,则亚晶块大小Dc 为/cos()()c c D K A λβθ=3.V oigt 近似函数积分宽度法设某 一 柯西函数Ic(x)及一高斯函数Ig(x ),则两者卷积后的 函数Iv(x)就是一个V oigt 函数.()()()()()v c g c g I x I x I x I y I x y dy ∞-∞=∙=-⎰当它们的积分宽度分别为βc ,βg ,βv 时,则可有如下满意近似公式:2/1(/)c v g v ββββ=-此法适用于0.63662<2W (βv )/βv <0.93949的大部分情况当晶粒碎化宽化与应变宽化同时存在时,上述l 和2方法均不适用,可用V oigt 近似函数法.理论考虑和实验结果两方面都表 明,应变宽化通常可以近似为高斯函数线形描述,而晶粒碎化效应 更接近柯西线形函数. 高斯函数:22x e α- 柯西函数:2211x α+若都是高斯型的,则B 2=b 2+βf 2若都是柯西型的,则B=b+β f有柯西,亦有高斯型,则21()ffBbββ=-(二)、线的宽度表示方法:三种表示方法:半宽度法、积分宽度法、方差法。
1、半宽度:线性在极大强度一半处(净强度)的总宽度 22B θθ'''=-半高2、积分宽度法:背景以上线形的积分强度除以峰值高度,()()122P maxI B I d I I θθ==⎰积分积分 上式积分宽度在数学可以等于高度等于峰值面积与实际线形相等一个矩形的宽度。
3、方差法测宽度:线形均方标准偏差,线形宽度方差定义为:质心和方差都有相加性的特点:所以实际测量质心和方差的计算采用下式:∑∑∆⋅∆⋅⋅=)2()2()2()2(2)2(θθθθθθI I())2()2()2()2()2(22θθθθθθ∆⋅∆⋅⋅-=∑∑I I W 实验测定:○1确定扫测衍射峰的范围,如:49.5~50.5。
○2确定增量δθ即将扫测范围10分几等分测, ○3由起始角起测量(2)I I B θ=-,在几个位置测,并将测量结果列成表: 编号 2θ)2(B I I -=θ)2(2θθI ⋅()2)2(2θθ- ())2()2(22θθθI ⋅-1 49.5 249.525n 50.52(2)(2)2(2)(2)I I θθθθθθ⋅⋅∆〈〉=⋅∆∑∑ ()222(2)(2)(2)(2)I W I θθθθθθ-〈〉⋅⋅∆=⋅∆∑∑()()22222(2)(2)22(2)(2)I d W I d θθθθθθθθθ∞-∞∞-∞-〈〉=〈-〈〉〉=⎰⎰θ″″二、测定方法和计算公式在无机非金属材料的科学研究和生产部门中,为了提高原料的及应活性,改善材料的显微结构状态,广泛采用超细粉;对某些材料,希望合成物具有微细晶粒的显微结构以提高其性能。
