2012数学建模校内赛试题
2012年数学建模C题

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): C我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期:年月日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):脑卒中发病环境因素分析及干预摘要:脑卒中(俗称脑中风)是目前威胁人类生命的严重疾病之一,为了让脑卒中高危人群能够及时采取干预措施,需要进行疾病的风险评估。
本文先对数据进行统计处理,然后分析各个量之间的关系,再建立数学模型,利用数据拟合计算各个量之间的函数关系,最后求解得出结论。
在问题一中,通过对脑卒中的发病人群进行了统计和分析,分别研究了四个不同年份的患者,将他们按不同年龄、不同性别以及不同职业分别进行划分,然后通过建表和作图将他们进行统计和分析,从而判断脑卒中在不同人群中的发病情况:男性比女性的发病率偏高,且男女的平均比为1.35:1;青少年患病率较低,占29%;中老年人患病率偏高,占70%,而且患病率逐年增加,平均年龄为69.77339,发病年龄最高的为76岁;农民、退休人员、工人的患病率比其他职业的人群高,其中农民发病率最高,为67.46%。
【2012高教社杯全国大学生数学建模竞赛赛题B】cumcm2012B附件7_小屋的建筑要求

全国大学生数学建模竞赛真题试卷复习材料附件7:小屋的建筑要求
限定小屋使用空间高度为:建筑屋顶最高点距地面高度≤5.4m, 室内使用空间最低净空高度距地面高度为≥2.8m;建筑总投影面积(包括挑檐、挑雨棚的投影面积)为≤74m2;建筑平面体型长边应≤15m,最短边应≥3m;建筑采光要求至少应满足窗地比(开窗面积与房间地板面积的比值,可不分朝向)≥0.2的要求;建筑节能要求应满足窗墙比(开窗面积与所在朝向墙面积的比值)南墙≤0.50、东西墙≤0.35、北墙≤0.30。
建筑设计朝向可以根据需要设计,允许偏离正南朝向。
河西学院第八届学科竞赛--2012数学建模竞赛题目
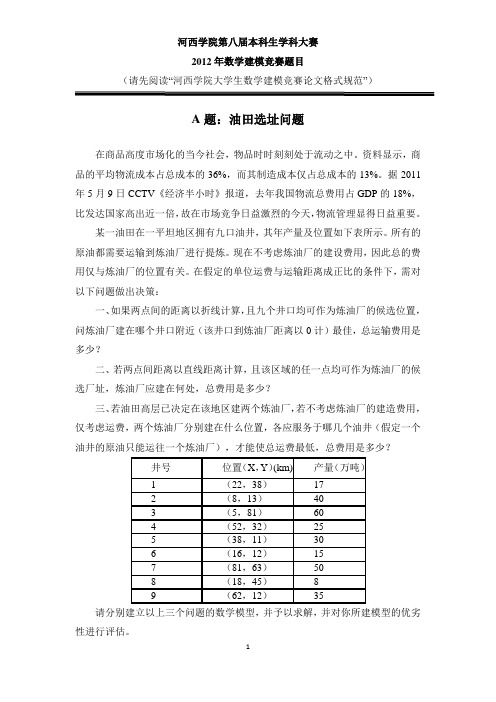
(请先阅读“河西学院大学生数学建模竞赛论文格式规范”)A题:油田选址问题在商品高度市场化的当今社会,物品时时刻刻处于流动之中。
资料显示,商品的平均物流成本占总成本的36%,而其制造成本仅占总成本的13%。
据2011年5月9日CCTV《经济半小时》报道,去年我国物流总费用占GDP的18%,比发达国家高出近一倍,故在市场竞争日益激烈的今天,物流管理显得日益重要。
某一油田在一平坦地区拥有九口油井,其年产量及位置如下表所示。
所有的原油都需要运输到炼油厂进行提炼。
现在不考虑炼油厂的建设费用,因此总的费用仅与炼油厂的位置有关。
在假定的单位运费与运输距离成正比的条件下,需对以下问题做出决策:一、如果两点间的距离以折线计算,且九个井口均可作为炼油厂的候选位置,问炼油厂建在哪个井口附近(该井口到炼油厂距离以0计)最佳,总运输费用是多少?二、若两点间距离以直线距离计算,且该区域的任一点均可作为炼油厂的候选厂址,炼油厂应建在何处,总费用是多少?三、若油田高层已决定在该地区建两个炼油厂,若不考虑炼油厂的建造费用,仅考虑运费,两个炼油厂分别建在什么位置,各应服务于哪几个油井(假定一个油井的原油只能运往一个炼油厂),才能使总运费最低,总费用是多少?请分别建立以上三个问题的数学模型,并予以求解,并对你所建模型的优劣性进行评估。
(请先阅读“河西学院大学生数学建模竞赛论文格式规范”)B题地理区域气温时间分布特征气温是人类环境的重要影响因子,在如今全球升温的大背景下,讨论一个地理区域的气温分布特征,对于衡量观测数据的准确性和气温预报有重要作用。
附件资料是按照地理位置和地理特征将某区域划分为三个小区:南区、中区和北区后,在三个不同小区域分别利用气象自动站进行全天24小时(每小时1次)的观测,试利用观测得到的数据分析温度分布特征,并建立数学模型对2007年冬季气温作出预测。
附件:DATA.xls(请先阅读“河西学院大学生数学建模竞赛论文格式规范”)C题:大学生综合素质测评办法评价大学生综合素质测评,是高校根据党的教育方针和教育目标,采用科学合理的方法,对大学生在一定时期内在校学习、生活等方面反映出来的素质表征信息,综合评定做出定量分析。
高教杯2012年数学建模A题

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): a我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期:年月日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):葡萄酒的评价摘要本文利用SPSS和MATLAB软件对葡萄酒评价问题进行了分析,综合采用了t检验、主成分分析、聚类分析和灰色关联度分析等方法,建立了数学模型,并设计了一套对葡萄酒质量的评价体系。
关于问题一:首先,对两组评酒员对同一种葡萄酒给出的评分结果进行处理;其次,采用t检验判断出两组评分结果存在显著性差异;最后,利用每一组评酒员对同一种葡萄酒的评分方差作为衡量依据,建立评分机制,评估两个小组所给结果的可信性,经分析第一组、第二组得分分别为13分、42分。
因此,第二组评酒员的评分结果更可信。
关于问题二:首先,对酿酒葡萄的理化指标进行主成分分析,挖掘出若干个影响酿酒葡萄理化指标的主要成分;其次,根据第一问的结果,将第二组评酒员的评分作为衡量葡萄酒质量的量化指标;最后,通过聚类分析将酿酒葡萄分为4个等级。
2012高教社杯全国大学生数学建模竞赛A题

2012高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们授权全国大学生数学建模竞赛组委会,可将我们的论文以任何形式进行公开展示(包括进行网上公示,在书籍、期刊和其他媒体进行正式或非正式发表等)。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): A我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):CXXY参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期: 2012年 09 月 10 日赛区评阅编号(由赛区组委会评阅前进行编号):2012高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):A题葡萄酒的评价摘要问题一:针对两组评酒员的评价结果需要进行多个平均数间的差异显著性检验,首先应该对数据进行正态分布检验,结论是每一个葡萄酒样品的评价得分都服从正态分布,之后利用SPSS软件进行两独立样本T检验模型进行显著性检验得出两组评酒员的评价结果有显著性差异,结合方差分析得出第二组评分更可信。
问题二:根据酿酒葡萄的理化指标采用聚类分析和主成分分析的方法模型对酿酒葡萄评价,再结合问题一中葡萄酒的质量评价,利用正态分布将两者标准化到统一的评分尺度中,对两者赋予不同的权重系数求总得分,进而对这些酿酒葡萄划分成5个等级。
2012数学建模试题

2012数学建模试题湖工商贸2011-2012学年第二学期《数学建模》课程考试试题(开卷)考试要求:1) 请同学们从三道试题中任选二题完成,写出详细的过程,模型的完成度是评分的主要标准。
2) 有意愿参加全国数模竞赛的同学,必须完成附加题,并在论文中附上联系方法。
3) 上交的论文必须为打印稿,并附上姓名、学号、专业、班级,由于信息缺失而导致无成绩,概不负责。
4) 交卷时间统一为6月8日上午,特殊情况的同学最迟6月23日上午交5) 6月16日上午由于四、六级考试,选修课停上。
1( 钢筋切割问题设某种规格的钢筋原材料每根长13 m,求解如下优化问题:,问至少需要购买原材料几根,如1) 现需要该种钢筋长度为4m的28根,长度为1.6m的30根何切割?2) 如需要该种钢筋长度为4m的28根,长度为1.6m的33根,长度为3.8m 的79根,长度为 2.4m的46根,问至少需要购买原材料几根,如何切割?请建立数学模型,解决上述问题。
2( 评价问题收集至少10所高校你自己对应年级和对应专业的学生课程安排表,或者收集本校10个不同专业大二学生课表安排,建立一个评价模型,来评价其课程安排的合理性,最终排出顺序。
3( 回归模型已知煤的有机成分主要为碳(C)、氢(H)、氧(O)、氮(N)等元素,由于变质程度不同,它们的含量(%)也不同,煤的性能也不同。
今搜集各种煤的样品10块,分别测得碳、氢、氧、氮与高发热量(卡/克)的含量如下表,试求高发热量与碳、氢、氧、氮的关系。
C H O N 高发热量69 5.5 24 1.5 670057 6 35 2 520082 4.3 12 1.9 840077 4.8 17 1.3 750059 6 33 1.9 540080 4.6 14 1.7 800064 5.8 29 1.7 600067 5.7 26 1.6 630062 5.9 30 1.9 570073 5 21 1.6 70004( 附加题不同类型汽车的能耗和使用成本问题传统汽车以汽油为动力原料,利用燃油发动机驱动汽车行驶。
2012年校内数学建模选拔赛试题
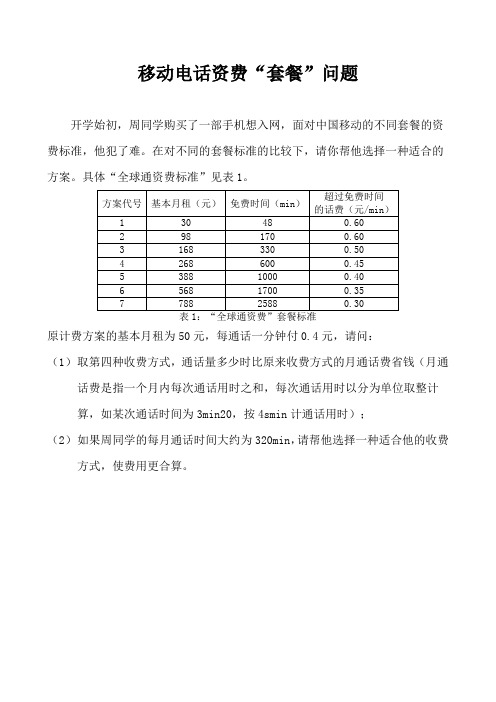
移动电话资费“套餐”问题开学始初,周同学购买了一部手机想入网,面对中国移动的不同套餐的资费标准,他犯了难。
在对不同的套餐标准的比较下,请你帮他选择一种适合的方案。
具体“全球通资费标准”见表1。
原计费方案的基本月租为50元,每通话一分钟付0.4元,请问:(1)取第四种收费方式,通话量多少时比原来收费方式的月通话费省钱(月通话费是指一个月内每次通话用时之和,每次通话用时以分为单位取整计算,如某次通话时间为3min20,按4smin计通话用时);(2)如果周同学的每月通话时间大约为320min,请帮他选择一种适合他的收费方式,使费用更合算。
内容摘要现在的生活中,到处都用手机了,可是很多人,不知道怎样省话费,怎样充分的利用话费,今天我们就一起来讨论这个问题,让每一个人都利用好自己的手机话费,充分的选择正确的话费套餐。
关键词套餐,省钱,数学模型一:问题重述购买手机入网,套餐有如表1的标准,请选同人,不同需求合适的套餐。
套餐表1原计费方案的基本月租为50元,每通话一分钟付0.4元,请问:(3)取第四种收费方式,通话量多少时比原来收费方式的月通话费省钱(月通话费是指一个月内每次通话用时之和,每次通话用时以分为单位取整计算,如某次通话时间为3min20,按4smin计通话用时);(4)如果周同学的每月通话时间大约为320min,请帮他选择一种适合他的收费方式,使费用更合算。
二:基本假设假设1:用户一个月都用这个套餐假设2:用户一个月客服都不增加其他的套餐 三:符号说明X 为总话费,y 总通话时间,z 为免费时间内通话的时间。
四:分析建模求解 1:在二基本假设的范围内,可得出: X=z*0.4 则由matlab 可得的如图:附录1 按照第4种收费的方式可得:X=268<50+0.45*600 所以有:X=268+0.45*(z-600)>50+0.4*z 0.85z>52 解得z>61.1764704 则由matlab 可得的如图:附录2 两个图组合图如:附录3第二小问:根据题目和第二步的假设可得一下三种方案可公选⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧--++=-+=-+=)17048(*60.0983006.0*)170(9860.0*)48(30z x z x z x 如附录3解这三个二元一次方程,当z=320时第二个方案最合适。
2012年“高教社杯”全国大学生数学建模竞赛(CUMCM)国家一等奖优秀论文C题目

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): C 我们的参赛报名号为(如果赛区设置报名号的话): 4052 所属学校(请填写完整的全名): XXXXXX参赛队员(打印并签名):1.2. (隐去论文作者相关信息等)3.指导教师或指导教师组负责人(打印并签名):日期: 2012 年 9 月 9 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):基于逐步回归的脑卒中发病环境因素分析及干预模型摘要本文通过建立合理的假设,对某地区2009-2010年脑卒中发病率与8种气象因素进行了相关分析,并经多元逐步回归建立了脑卒中发病率的预报模型进行了定量分析,得到了较为合理的结论。
考虑到发病率与气象因素的复杂关系,在逐步线性回归模型的基础上,引进广义线性回归模型(GLM)进行推广。
针对问题一,本文对性别、年龄段、职业和时间序列以及4年的平均发病例数进行统计和分析,在删除了一些缺失或失真数据的基础上,对数据分别进行整理分析。
最后,在性别方面,得到脑卒中发病率男性比女性的高。
从年龄结构看,发病人数主要集中在50~90这一年龄区间内,其所占比例达81.10%。
从职业结构看,农民的发病率最大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年北京理工大学珠海学院
数学建模校内赛试题
A题:铁皮罐下料问题
某厂计划生产密封圆柱形铁皮罐,容积为1升。
所用原料为1米×2米的铁皮原料。
考虑下列问题
(1)为方便起见,将上下盖所使用的圆形原料和侧面所使用的长方形原料分别在不同的铁皮原料上裁剪,请设计其宽高比,使用料最省。
(2)大规模生产时,只考虑节省原料问题。
如何设计铁罐宽高比和下料方案(可以在同一张铁皮原料上将上下盖所使用的圆形原料和侧面所使用的长方形原料混合裁剪),使用料最省?
(3)生产铁皮罐时,需要将铁皮原料预留接口,这样会使各部分下料尺寸比容积要求加大,如果考虑罐体宽高比和下料方案?
B题:楼盘定价问题
众所周知,房价问题已经是影响到民生的头等问题。
针对节节攀高的房价,国家通过一系列宏观调控来提高投机资金的炒作成本,比如加息等。
而在部分大城市,如北京、上海、广州、深圳还出台了限购令,更有甚者如珠海限购限价,所有的这一切都是为了房价平稳的着陆,理性的回归。
下表是珠海、中山、江门部分楼盘的销售均价。
一个楼盘的销售价格与它所在的城市、交通位置、开发商品牌、是否精装、户型等都有关。
试用以上信息结合城市具体政策建立数学模型来确定表中红色楼盘的销售价格,详细说明分析的思路,并给出推导过程。
答题要求:
1. 请于A、B两题中任选一题作答。
2. 根据上述条件,建立问题的数学模型,并独立完成数学建模论文。
以假设的合理性、建模的创造性、结果的准确性和论文表述的清晰性为评分标准。
交卷时间与方式:
1.交卷时间地点:
2011年4月23日(周一)下午5:30前送至HE307;
2.交卷方式:
论文需采用电子稿,用A4纸单面打印装订,将纸质版送至HE307;并将电子稿以email形式发送至邮箱wahh0524@ (如不按时提交答卷,将视为自动放弃参赛资格)。
