非线性回归分析
《非线性回归分析》课件
封装式
• 基于模型的错误率和复 杂性进行特征选择。
• 常用的封装方法包括递 归特征消除法和遗传算 法等。
嵌入式
• 特征选择和模型训练同 时进行。
• 与算法结合在一起的特 征选择方法,例如正则 化(Lasso、Ridge)。
数据处理方法:缺失值填充、异常值 处理等
1
网格搜索
通过预定义的参数空间中的方格进行搜
随机搜索
2
索。
在预定义的参数空间中进行随机搜索。
3
贝叶斯调参
使用贝叶斯优化方法对超参数进行优化。
集成学习在非线性回归中的应用
集成学习是一种将若干个基学习器集成在一起以获得更好分类效果的方法,也可以用于非线性回归建模中。
1 堆叠
使用多层模型来组成一个 超级学习器,每个模型继 承前一模型的输出做为自 己的输入。
不可避免地存在数据缺失、异常值等问题,需要使用相应的方法对其进行处理。这是非线性回归 分析中至关重要的一环。
1 缺失值填充
常见的方法包括插值法、代入法和主成分分析等。
2 异常值处理
常见的方法包括删除、截尾、平滑等。
3 特征缩放和标准化
为了提高模型的计算速度和准确性,需要对特征进行缩放和标准化。
偏差-方差平衡与模型复杂度
一种广泛用于图像识别和计算机 视觉领域的神经网络。
循环神经网络
一种用于处理序列数据的神经网 络,如自然语言处理。
sklearn库在非线性回归中的应用
scikit-learn是Python中最受欢迎的机器学习库之一,可以用于非线性回归的建模、评估和调参。
1 模型建立
scikit-learn提供各种非线 性回归算法的实现,如 KNN回归、决策树回归和 支持向量机回归等。
非线性回归分析的入门知识

非线性回归分析的入门知识在统计学和机器学习领域,回归分析是一种重要的数据分析方法,用于研究自变量和因变量之间的关系。
在实际问题中,很多情况下自变量和因变量之间的关系并不是简单的线性关系,而是呈现出一种复杂的非线性关系。
因此,非线性回归分析就应运而生,用于描述和预测这种非线性关系。
本文将介绍非线性回归分析的入门知识,包括非线性回归模型的基本概念、常见的非线性回归模型以及参数估计方法等内容。
一、非线性回归模型的基本概念在回归分析中,线性回归模型是最简单和最常用的模型之一,其数学表达式为:$$Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + ... + \beta_pX_p +\varepsilon$$其中,$Y$表示因变量,$X_1, X_2, ..., X_p$表示自变量,$\beta_0, \beta_1, \beta_2, ..., \beta_p$表示模型的参数,$\varepsilon$表示误差项。
线性回归模型的关键特点是因变量$Y$与自变量$X$之间呈线性关系。
而非线性回归模型则允许因变量$Y$与自变量$X$之间呈现非线性关系,其数学表达式可以是各种形式的非线性函数,例如指数函数、对数函数、多项式函数等。
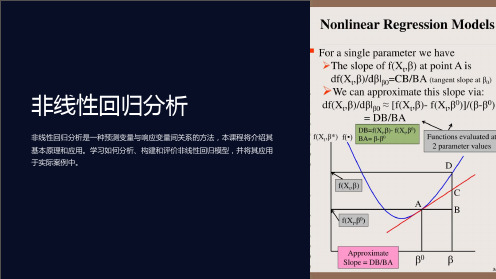
一般来说,非线性回归模型可以表示为:$$Y = f(X, \beta) + \varepsilon$$其中,$f(X, \beta)$表示非线性函数,$\beta$表示模型的参数。
非线性回归模型的关键在于确定合适的非线性函数形式$f(X,\beta)$以及估计参数$\beta$。
二、常见的非线性回归模型1. 多项式回归模型多项式回归模型是一种简单且常见的非线性回归模型,其形式为: $$Y = \beta_0 + \beta_1X + \beta_2X^2 + ... + \beta_nX^n +\varepsilon$$其中,$X^2, X^3, ..., X^n$表示自变量$X$的高次项,$\beta_0, \beta_1, \beta_2, ..., \beta_n$表示模型的参数。
回归分析非线性回归

回归分析非线性回归回归分析是用于探究自变量和因变量之间关系的一种统计方法,在实际应用中,所研究的问题往往并不是简单地呈线性关系。
为了更准确地描述变量之间的复杂关系,我们需要使用非线性回归模型。
非线性回归指的是自变量与因变量之间的关系不是简单的线性关系,而是可以用其他非线性函数更好地拟合的情况。
这样的非线性函数可以是多项式函数、指数函数、对数函数等等。
非线性回归可以更好地反映实际问题的实际情况,并且通常能够提供更准确的预测结果。
在非线性回归分析中,我们需要确定非线性函数的形式以及确定函数中的参数。
对于确定非线性函数的形式,一般来说,可以通过观察数据的散点图、经验和理论分析来选择。
根据选择的非线性函数形式,我们可以使用最小二乘法等方法来确定函数中的参数。
以一个简单的例子来说明非线性回归的具体步骤。
假设我们想要研究一个人的年龄和体重之间的关系,我们可以选择一个二次多项式模型来描述这个关系。
我们的非线性回归模型可以写作:体重=β₀+β₁×年龄+β₂×年龄²+ε其中,体重是因变量,年龄是自变量,ε是误差项。
我们的目标是确定模型中的参数β₀、β₁和β₂的值,使得模型最好地拟合观察到的数据。
为了实现这个目标,我们可以使用最小二乘法来估计参数的值。
最小二乘法是一种常用的参数估计方法,它通过最小化观测值与模型预测值之间的离差平方和来确定参数的值。
通过最小二乘法估计出的参数值,可以用于建立非线性回归模型,从而对未来的数据进行预测。
除了使用最小二乘法估计参数值之外,我们还可以使用其他的优化算法如牛顿法或梯度下降法来估计参数的值。
这些方法的选择通常取决于模型形式的复杂程度、参数数量以及数据量等因素。
需要注意的是,非线性回归模型的参数估计和预测结果都受到初始值的选择和模型形式的选择的影响。
因此,在进行非线性回归分析时,我们需要注意选择合适的初始值和合适的模型形式,以获得更准确的结果。
在实际应用中,非线性回归可以用于多个领域,比如医学、经济学、工程学等。
回归分析非线性回归

回归分析非线性回归回归分析是一种用于研究自变量与因变量之间关系的统计分析方法。
在回归分析中,我们使用自变量来解释因变量的变化,并建立一个数学模型来描述这种关系。
通常情况下,我们假设自变量与因变量之间是线性关系。
因此,在大多数回归分析应用中,我们使用线性回归模型。
然而,有时候我们可能会发现实际数据不符合线性关系的假设。
这时,我们就需要使用非线性回归模型来更好地解释数据。
非线性回归分析是一种通过建立非线性模型来描述自变量和因变量之间关系的方法。
在这种情况下,模型可以是各种形式的非线性函数,如指数函数、对数函数、多项式函数等。
非线性回归模型的形式取决于实际数据。
非线性回归模型的建立通常包括以下几个步骤:1.数据收集:首先需要收集与自变量和因变量相关的数据。
这些数据应该能够反映出二者之间的关系。
2.模型选择:根据实际情况选择合适的非线性模型。
常见的非线性模型有指数模型、对数模型、幂函数等。
3.参数估计:使用最小二乘法或其他拟合方法来估计模型中的参数。
这些参数描述了自变量和因变量之间的关系。
4.模型检验:对估计得到的模型进行检验,评估模型的拟合程度。
常见的检验方法有残差分析、F检验、t检验等。
5.模型解释与预测:解释模型的参数和拟合程度,根据模型进行预测和分析。
非线性回归分析的主要优点是可以更准确地描述自变量和因变量之间的关系。
与线性回归不同,非线性回归可以拟合一些复杂的实际情况,并提供更准确的预测。
此外,非线性回归还可以帮助发现自变量和因变量之间的非线性效应。
然而,非线性回归模型的建立和分析相对复杂。
首先,选择适当的非线性模型需要一定的经验和专业知识。
其次,参数估计和模型检验也可能更加困难。
因此,在进行非线性回归分析时,需要谨慎选择合适的模型和方法。
最后,非线性回归分析还需要考虑共线性、异方差性、多重共线性等统计问题。
这些问题可能影响到模型的稳定性和可靠性,需要在分析过程中加以注意。
总之,非线性回归分析是一种用于解释自变量和因变量之间非线性关系的方法。
《非线性回归》课件

灵活性高
非线性回归模型形式多样,可以根据 实际数据和问题选择合适的模型,能 够更好地适应数据变化。
解释性强
非线性回归模型可以提供直观和易于 理解的解释结果,有助于更好地理解 数据和现象。
预测准确
非线性回归模型在某些情况下可以提 供更准确的预测结果,尤其是在数据 存在非线性关系的情况下。
缺点
模型选择主观性
势。
政策制定依据
政府和决策者可以利用非线性回归模型来评估不同政策方案的影响,从而制定更符合实 际情况的政策。例如,通过分析税收政策和经济增长之间的关系,可以制定更合理的税
收政策。
生物学领域
生态学研究
在生态学研究中,非线性回归模型被广 泛应用于分析物种数量变化、种群动态 和生态系统稳定性等方面。通过建立非 线性回归模型,可以揭示生态系统中物 种之间的相互作用和环境因素对种群变 化的影响。
模型诊断与检验
诊断图
通过绘制诊断图,可以直观地观察模型是否满足回归分析的假设条件,如线性关系、误差同方差性等 。
显著性检验
通过显著性检验,如F检验、t检验等,可以检验模型中各个参数的显著性水平,从而判断模型是否具 有统计意义。
04
非线性回归在实践中的应用
经济学领域
描述经济现象
非线性回归模型可以用来描述和解释经济现象,例如消费行为、投资回报、经济增长等 。通过建立非线性回归模型,可以分析影响经济指标的各种因素,并预测未来的发展趋
VS
生物医学研究
在生物医学研究中,非线性回归模型被用 于分析药物疗效、疾病传播和生理过程等 方面。例如,通过分析药物浓度与治疗效 果之间的关系,可以制定更有效的治疗方 案。
医学领域
流行病学研究
在流行病学研究中,非线性回归模型被用于 分析疾病发病率和死亡率与各种因素之间的 关系。通过建立非线性回归模型,可以揭示 环境因素、生活方式和遗传因素对健康的影 响。
非线性回归分析

非线性回归分析随着数据科学和机器学习的发展,回归分析成为了数据分析领域中一种常用的统计分析方法。
线性回归和非线性回归是回归分析的两种主要方法,本文将重点探讨非线性回归分析的原理、应用以及实现方法。
一、非线性回归分析原理非线性回归是指因变量和自变量之间的关系不能用线性方程来描述的情况。
在非线性回归分析中,自变量可以是任意类型的变量,包括数值型变量和分类变量。
而因变量的关系通常通过非线性函数来建模,例如指数函数、对数函数、幂函数等。
非线性回归模型的一般形式如下:Y = f(X, β) + ε其中,Y表示因变量,X表示自变量,β表示回归系数,f表示非线性函数,ε表示误差。
二、非线性回归分析的应用非线性回归分析在实际应用中非常广泛,以下是几个常见的应用领域:1. 生物科学领域:非线性回归可用于研究生物学中的生长过程、药物剂量与效应之间的关系等。
2. 经济学领域:非线性回归可用于经济学中的生产函数、消费函数等的建模与分析。
3. 医学领域:非线性回归可用于医学中的病理学研究、药物研发等方面。
4. 金融领域:非线性回归可用于金融学中的股票价格预测、风险控制等问题。
三、非线性回归分析的实现方法非线性回归分析的实现通常涉及到模型选择、参数估计和模型诊断等步骤。
1. 模型选择:在进行非线性回归分析前,首先需选择适合的非线性模型来拟合数据。
可以根据领域知识或者采用试错法进行模型选择。
2. 参数估计:参数估计是非线性回归分析的核心步骤。
常用的参数估计方法有最小二乘法、最大似然估计法等。
3. 模型诊断:模型诊断主要用于评估拟合模型的质量。
通过分析残差、偏差、方差等指标来评估模型的拟合程度,进而判断模型是否适合。
四、总结非线性回归分析是一种常用的统计分析方法,可应用于各个领域的数据分析任务中。
通过选择适合的非线性模型,进行参数估计和模型诊断,可以有效地拟合和分析非线性关系。
在实际应用中,需要根据具体领域和问题的特点来选择合适的非线性回归方法,以提高分析结果的准确性和可解释性。
非线性回归分析与曲线拟合方法

非线性回归分析与曲线拟合方法回归分析是一种常见的统计分析方法,用于研究自变量与因变量之间的关系。
在实际应用中,很多数据并不符合线性关系,而是呈现出曲线形式。
这时,我们就需要使用非线性回归分析和曲线拟合方法来更好地描述数据的规律。
一、非线性回归分析的基本原理非线性回归分析是一种通过拟合非线性方程来描述自变量与因变量之间关系的方法。
与线性回归不同,非线性回归可以更准确地反映数据的特点。
在非线性回归分析中,我们需要选择适当的非线性模型,并利用最小二乘法来估计模型的参数。
二、常见的非线性回归模型1. 多项式回归模型:多项式回归是一种常见的非线性回归模型,它通过多项式方程来拟合数据。
多项式回归模型可以描述数据的曲线特征,但容易出现过拟合问题。
2. 指数回归模型:指数回归模型适用于自变量与因变量呈指数关系的情况。
指数回归模型可以描述数据的增长或衰减趋势,常用于描述生物学、物理学等领域的数据。
3. 对数回归模型:对数回归模型适用于自变量与因变量呈对数关系的情况。
对数回归模型可以描述数据的增长速度,常用于描述经济学、金融学等领域的数据。
4. S形曲线模型:S形曲线模型适用于自变量与因变量呈S形关系的情况。
S形曲线模型可以描述数据的增长或衰减过程,常用于描述市场营销、人口增长等领域的数据。
三、曲线拟合方法曲线拟合是一种通过选择合适的曲线形状来拟合数据的方法。
在曲线拟合过程中,我们需要根据数据的特点选择适当的拟合方法。
1. 最小二乘法:最小二乘法是一种常用的曲线拟合方法,通过最小化观测值与拟合值之间的残差平方和来确定拟合曲线的参数。
2. 非线性最小二乘法:非线性最小二乘法是一种用于拟合非线性模型的方法,它通过最小化观测值与拟合值之间的残差平方和来确定模型的参数。
3. 曲线拟合软件:除了手动选择拟合方法,我们还可以使用曲线拟合软件来自动拟合数据。
常见的曲线拟合软件包括MATLAB、Python的SciPy库等。
四、应用实例非线性回归分析和曲线拟合方法在实际应用中有着广泛的应用。
非线性回归分析江南大学张荷观.pptx

记 (1, 2 ,, p ) , 高斯–牛顿法的具体方法如下。
第9页/共47页
(1)
先取参数的一组初值 B0 (b10 , b20 ,, bp0 ) , 根据泰勒级数并 只取线性项, 得
y f (x1, x2 ,, xk ;b10 , b20 ,, bp0 )
p i 1
f
i
b B0 i0
p f
i1 i
B0 i '
第10页/共47页
(3-6)
最小二乘估计
令
MLeabharlann yf(x1 , x2 ,, xk ;b10 , b20 ,, bp0 )
p i 1
f
i
b B0 i0
Zi
f
i
B0 , i 1,2,, p
对给定的初始值 B0 , M 和 Zi 都是确定的。则得线性回归模型
停止迭代。 在实际工作中这几个标准可替换, 但无明显优劣, 一般可同时
使用。
第23页/共47页
第三节 非线性回归评价和假设捡验 与线性回归分析一样,非线性回归分析在建立回归方程后进行评 价和捡验。主要有回归方程拟合度的评价,以及回归方程和回归系数 的显著性捡验等。非线性回归的最小二乘估计不是BLUE, 但一般条 件下是一致估计。
直到满足要求, 即得参数的最小二乘估计。
直接搜索法和格点搜索法都是低效的, 在实际工作中很少采用。
第8页/共47页
三、高斯–牛顿(Gauss - Newton)法 高斯–牛顿法是一种常用的迭代法。 非线性回归模型不能通过变换转化为线性回归模型, 但可以利 用泰勒展开式转化为线性回归模型。设非线性回归模型
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
bˆ luv / luu 0.00082917
aˆ v ubˆ 0.00896663
y
x
0.00082917 0.00896663x
9
用类似的方法可以得出其它三个曲 线回归方程,它们分别是:
y 106.3147 3.9466ln x y 106.3013 1.1947 x
y 100 11.7506e1.1256/x
10
曲线回归方程的比较
我们上面得到了四个曲线回归方程,通常可采用如
下二个指标进行选择。 (1)决定系数R2:类似于一元线性回归方程中相关系
数,决定系数定义为:
R2 1
( yi yi )2 ( yi y )2
R2越大,说明残差越小,回归曲线拟合越好, R2从总
体上给出一个拟合好坏程度的度量。
11
(2)剩余标准差s:类似于一元线性回归中标准差的估计 公式,此剩余标准差可用残差平方和来获得,即
s
( yi yi )2
n2
s为诸观测点yi与由曲线给出的拟合值 yˆi 间的平均偏离程 度的度量,s越小,方程越好。
12
在观测数据给定后,不同的曲线选择不会影响
n
的取值,但会影响到残差平方和 ( yi y)2的取值。 i 1
18 111.00
19 111.20
4
确定可能的函数形式
为对数据进行分析,首先描出数据 的散点图,判断两个变量之间可 能的函数关系,图是本例的散点 图。
观测这13个点构成的散点图,我 们可以看到它们并不接近一条直 线,用曲线拟合这些点应该是更 恰当的,这里就涉及如何选择曲 线函数形式的问题。
8 y (%)
3
钢包的重量y与试验次数x数据
序号 1 2 3 4 5 6 7
x
y
序号
2 106.42 8
3 108.20 9
4 109.58 10
5 109.50 11
7 110.00 12
8 109.93 13
10 110.49
下面我们分三步进行。
x
y
11 110.59
14 110.60
15 110.90
16 110.76
6
本例中,散点图呈现呈现一个明显的向上且上 凸的趋势,可能选择的函数关系有很多,比如, 我们可以给出如下四个曲线函数:
1) 1/y=a+b/x 2) y=a+blnx 3) y a b x 4) y 100 a ex/b (b 0)
在初步选出可能的函数关系(即方程)后,我们必 须解决两个问题:如何估计所选方程中的参数? 如何评价所选不同方程的优劣?
8
参数估计计算表
ui 2.05088194
u 0.15776015
ui2 0.53721798
nu 2 0.32354744
n 13
uivi 0.01883495
nuv 0.01865778
vi 0.11826672
v 0.00909744
luu 0.21367054
luv 0.00017717
年份
1981 1982 1983 1984 1985 1986 1987 1988 1989 1990 合计
商品流通费用率(%) yi
7.0 6.2 5.8 5.3 5.0 4.6 4.5 4.4 4.2 4.0 51.0
商品零售额(万元)xi
10.2 11.7 13.0 15.0 16.5 19.0 22.0 25.0 28.5 32.0 -
R2 1 0.5743 0.9729, s 0.5743 0.2285
21.2105
13 2
其它三个方程的决定系数及剩余标准差可同 样计算,我们将它们列在表中。
14
四种曲线回归 决定系数及剩余标准差
模型编号 R2
s
(1) 0.9729 0.2285
(2) 0.8773 0.4864
(3) 0.7851 0.6437
回顾-一元一次线性回归
步骤:
指标评价 回归公式
1.观察散点图 2.判断是什么关系; 3. 回归参数计算; 4. 判断系数; 5.显著性检验(注意H0) 6.失拟合检验(注意需要的条件)
相关系数,判断系数
显著性检验 H0假设的含义;方差分析表;F(1,n-2)
失拟合检验 条件?F(m-2,n-m)
1
回归分析内容
7
6
5
4
3
x (万元)
5
10
15
20
25
30
35
图 6.5.1 商品零售额与商品流通费用率的散点图
5
首先,如果可由专业知识确定回归函数形式,则应 尽可能利用专业知识。当若不能有专业知识加以确 定函数形式,则可将散点图与一些常见的函数关系 的图形进行比较,选择几个可能的函数形式,然后 使用统计方法在这些函数形式之间进行比较,最后 确定合适的曲线回归方程。为此,必须了解常见的 曲线函数的图形,。
(4) 0.9623 0.2696
可以看出,第一个曲线方程的决定系数最大,剩 余标准差最小,在这四个曲线回归方程中,不论 用哪个标准,都是第一个方程拟合得最好。因此, 近似得比较好的定量关系式就是
y
x
0.00082917 0.00896663x
15
例子
例 设某商店 1991~2000 年的商品流通费用率和商品零售额资料如下表:
因此,对选择的曲线而言,决定系数和剩余标准差
n
都取决于残差平方和 (yi yi )2,从而,两种选择准
i 1
n
则是一致的,只是从两个不同侧面作出评价。 (yi yi )2
i 1
13
表给出第一个曲线回归方程的残差平方和的
计算过程,
由于n=13,
13
(
yi
y)2
0.5743
, 故其
i 1
决定系数及剩余标准差分别为:
一元线性
一元非线性 带虚拟变量 多元线性
步骤: 1.观察散点图,2.判断是什么关 系,3. 回归,4. 判断系数;5。显著 性检查(注意H0),6.失拟合检验 (注意需要的条件)
多元非线性和 逐步回归
Logistic回归
2
一次非线性回归
炼钢厂出钢水时用的钢包,在使用过程中由于钢水 及炉渣对耐火材料的浸蚀,其容积不断增大。现在钢 包的容积用盛满钢水时的重量y (kg)表示,相应的试 验次数用x表示。数据见表,要找出y 与x的定量关系 表达式。
7
对上述非线性函数,参数估计最常用的方法 是“线性化”方法。 以1/y=a+b/x为例,为了能采用一元线性回归 分析方法,我们作如下变换u=1/x,v=1/y 则曲线函数就化为如下的直线v=bu 这是理论回归函数。对数据而言,回归方程为
vi=a+ bui + i
于是可用一元线性回归的方法估计出a,b。
