证明直线与圆相切是一类常见题目
证明直线与圆相切是一类常见题目

证明直线与圆相切是一类常见题目,解决这类问题常用的方法有两种。
一、连半径,证垂直
若图形中已给出直线与圆的公共点,但未给出过点的半径,则可先连结过此点的半径,再证其与直线垂直。
例1如图(1)所示,在△ABC中,AB=AC,以AB为直径作圆交于BC于D,作DE⊥AC于E。
求证:DE 为⊙O的切线。
例2如图(2)所示,AB是⊙O的直径,过A点作⊙O的切线,在切线上任取一点C,连结OC交⊙O 于D,连结BD并延长交AC于E,求证:CD是△ADE外接圆的切线。
证明:取AE的中点F,连结FD。
∵AB为直径,
∴AD⊥BD
∵FD=FE(=FA)
∴∠FED=∠FDE
∵∠CDE=∠BDO=∠B
∠FEB+∠B=90°
∴∠FDE+∠CDE=90°
即FD⊥CD
∴CD是△ADE的外接圆的切线。
二、作垂线,证半径
若图形中未给出直线与圆的公共点,则需先过圆心作该直线的垂线,再证垂足到圆心的距离等于半径。
例3 如图(3)所示,已知AB是⊙O的直径,AC⊥L于C,BD⊥L于D,且AC+BD=AB。
求证:直线L 与⊙O相切。
证明:过O作OE⊥L于E。
∵AC⊥L,BD⊥L,
∴AC∥OE∥BD。
又AO=OB,∴CE=CD
从而OE为梯形ACDB的中位线。
∴OE=(AC+BD)=AB
即垂足E到圆心O的距离等于半径。
故直线L与⊙O相切。
证明直线和圆相切的常见方法

证明直线和圆相切的常见方法证明直线和圆相切,一般有两种情况:一、已知直线与圆的公共点时只需连接该公共点和圆心,证明该半径垂直于已知直线例1如图1,B、C是⊙O上的点,线段AB经过圆心O,连接AC、BC,过点C作CD⊥AB于D,∠ACD=2∠B.AC是⊙O的切线吗?为什么?解:AC是⊙O的切线.理由:连接OC,因为OC=OB,所以∠OCB=∠B.因为∠COD是△BOC的外角,所以∠COD=∠OCB+∠B=2∠B.因为∠ACD=2∠B,所以∠ACD=∠COD.因为CD⊥AB于D,所以∠DCO+∠COD=90°.所以∠DCO+∠ACD=90°.即OC⊥AC.因为C为⊙O上的点,所以AC是⊙O的切线.例2 如图2,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB 的延长线上的一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.求证:DE是⊙O的切线.证明:连接OC,则OA=OC,所以∠CAO=∠ACO,因为AC平分∠EAB,所以∠EAC=∠CAO=∠ACO,所以AE∥CO,又AE⊥DE,所以CO⊥DE,所以DE是⊙O的切线.二、直线与圆的公共点未知时须通过圆心作已知直线的垂直线段,证明此垂线段的长等于半径例3如图3,AO是△ABC的中线,⊙O与AB边相切于点D.(1)要使⊙O与AC边也相切,应增加条件_______________________.(任写一个)(2)增加条件后,请你证明⊙O与AC边相切.解:(1)答案不唯一,可以是∠B=∠C,AB=AC,∠BAO=∠CAO,AO⊥BC 等.(2)增加条件∠B=∠C后,⊙O与AC边相切.证明:连接OD,作OE⊥AC,垂足为E.因为⊙O与AB相切于点D,所以∠BDO=∠CEO=90°.因为AO是△ABC的中线,所以OB=OC.又因为∠B=∠C,所以△BDO≌△CEO,所以OE=OD.因为OD是⊙O的半径,所以OE是⊙O的半径.所以⊙O与AC边相切.。
圆的切线的判定方法练习题
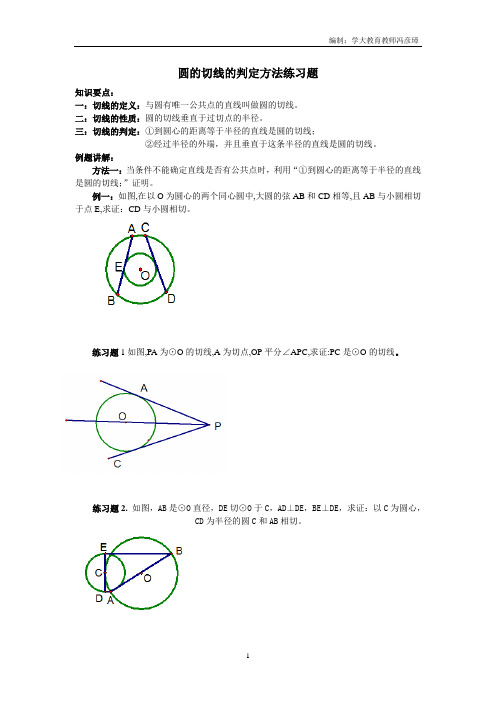
圆的切线的判定方法练习题
知识要点:
一:切线的定义:与圆有唯一公共点的直线叫做圆的切线。
二:切线的性质:圆的切线垂直于过切点的半径。
三:切线的判定:①到圆心的距离等于半径的直线是圆的切线;
②经过半径的外端,并且垂直于这条半径的直线是圆的切线。
例题讲解:
方法一:当条件不能确定直线是否有公共点时,利用“①到圆心的距离等于半径的直线是圆的切线;”证明。
例一:如图,在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E,求证:CD与小圆相切。
练习题1如图,PA为⊙O的切线,A为切点,OP平分∠APC,求证:PC是⊙O的切线。
练习题2.如图,AB是⊙O直径,DE切⊙O于C,AD⊥DE,BE⊥DE,求证:以C为圆心,
CD为半径的圆C和AB相切。
练习题3.如图,在以O为圆心的两个同心圆中,AB经过圆心O,且于小圆相交于点A、于大圆相交于点B。
小圆的切线AC于大圆相交于点D,且CO平分∠ACB。
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由;
(3)若AB=4cm,BC=5cm,求大圆与小圆围成的圆环的面积。
怎样证明一条直线是圆的切线的专题练习

怎样证明一条直线是圆的切线的专题练习圆这一章的是初中数学教学的重点内容,也是难点。
是中考的重要内容,占据的分数比例比较大,是综合性特别强,难度特别大的题目。
一般放在压轴的位置。
中考数学题一般分为三问或者四问来出题,第一问就是证明一条直线是圆的切线。
切线的证明方法大体上有两种:一种是证明所给直线与半径夹角为直角;另一种是证明圆心的直线的距离等于圆的半径。
说起来很简单,但是通过自己四十来年教学和研究发现,学生做起来,比较困难,原因之一是大部分学生没有充分利用好题目中所给的条件,二是利用的所给角比较多,不知道从哪里作为突破口。
下面我就整理了一些专门证明直线是圆的切线题目,提供广大初中学生,供你们做一做,按照我题目中设计意境提供的思路,具体题中体会一下,总结一下。
一定会对你今后的学习有很大帮助。
一.证明所给直线与圆的半径垂直(一)通过角的计算证明所给直线与半径夹角为直角。
1.在△ABC 中,AB=AC,以AB 为直径的⊙O 分别交AC,BC 于点D,E.点F 在AC 的延长线上,∠CBF=21∠CAB.判断直线BF 与⊙O 的位置关系,并给出证明;2.如图,平行四边形ABCD ,以AB 直径的⊙O 经过D,E 是⊙O 上一点,且∠AED=450.试判断CD 与⊙O 的位置关系,并说明理由;3..如图,AB 是⊙O 的直径,点C 在⊙O 上,经过C 的直线与AB 的延长线交于P,AC=PC,∠COB=2∠PCB.求证:CP 为⊙O 的切线.4..在△ABC 中,∠ACB=900,D 是边AB 上一点,∠A=2∠DCB,E 是边BC 上一点,以EC 为直径的⊙O 经过点D.求证:AB 为⊙O 的切线.A5.如图,AB 是⊙O 的直径,C 为⊙O 上一点,过点C 作直线MN 满足∠MCA=∠CBA..求证:直线MN 为⊙O 的切线.6.如图,点A,B,C 分别为⊙O 上的点,∠B=600,AC=3,CD 是⊙O 的直径,P 是CD 延长线上一点,且AP=AC.求证:AP 为⊙O 的切线。
圆的切线的判定与性质练习题

圆的切线的判定与性质一、若直线l过⊙O上某一点A,证明l是⊙O的切线,只需连OA,证明OA⊥l就行了,简称“连半径,证垂直”,难点在于如何证明两线垂直.例1如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于D,交AC于E,B为切点的切线交OD延长线于F.求证:EF与⊙O相切.例2如图,AD是∠BAC的平分线,P为BC延长线上一点,且PA=PD. 求证:PA与⊙O相切.二、若直线l与⊙O没有已知的公共点,又要证明l是⊙O的切线,只需作OA⊥l,A为垂足,证明OA是⊙O的半径就行了,简称:“作垂直;证半径”例3 如图,AB=AC,D为BC中点,⊙D与AB切于E点.求证:AC与⊙D相切.例3已知:如图,AC,BD与⊙O切于A、B,且AC∥BD,若∠COD=900.求证:CD是⊙O的切线.练习题1.如图,AB=AC,AB是⊙O的直径,⊙O交BC于D,DM⊥AC于M求证:DM与⊙O相切.3(2008黄冈市)已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.求证:DE是⊙O的切线.4. 如图,ABCD是正方形,G是BC延长线上一点,AG交BD于E,交CD于F.求证:CE与△CFG的外接圆相切.5.如图,AB是⊙O的直径,∠BAC=30°,M是OA上一点,过M作AB的垂线交AC于点N,交BC 的延长线于点E,直线CF交EN于点F,且∠ECF=∠E.(1)证明CF是⊙O的切线;(2)设⊙O的半径为1,且AC=CE,求MO的长.6.如图,已知⊙O1与⊙O2交于A,B,⊙O1的半径为17,⊙O 2的半径为10,O 1O 2=21,求AB 的长.7.如图,已知⊙O 1与⊙O 2交于A ,B 两点,过A 的直线交两圆于C ,D 两点,•G•为CD 的中点,BG 及其延长线交⊙O 1,⊙O 2于E ,F ,连结DF ,CE ,求证:CE=DF .8.某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上,向内放入两个半径为5cm 的钢球,测得上面一个钢球顶部高DC=16cm(钢管的轴截面如图所示), 求钢管的内直径AD 的长9.如图,⊙O 1和⊙O 2交于A 、B ,⊙O 1弦交⊙O 2于E ,⊙O 2弦AD 交⊙O 1于F ,若∠CAB=∠DAB ,求证:CE=DF 。
关于解决直线与圆的位置关系问题的几种常用方法

关于解决直线与圆的位置关系问题的几种常用方法李志民1 直线与圆的位置关系有三种:相交、相切、相离。
判断直线与圆的位置关系常见的有三种方法:判别式 相交1.1代数法: 相切Δ=b2-4ac 相离1.2 几何法:利用圆心到直线的距离d和圆半径r的大小关系:d<r 相交,d=r 相切,d>r相离(三)点与圆的位置关系法:若直线恒过定点且定点在圆内,可判断直线与圆相交.此法适用于动直线问题。
2 计算直线被圆截得的弦长的常用方法2.1 几何方法运用弦心距(即圆心到直线的距离)、弦长的一半及半径构成直角三角形计算。
2.2 代数方法一是直接求出直线与圆的交点坐标,再利用两点间的距离公式得出;二是运用韦达定理及弦长公式|AB|= |x A-x B|=.]4))[(1(22BABAxxxxk-++说明:圆的弦长、弦心距的计算常用几何方法。
3 求过点P(x0,y0)的圆x2+y2=r2的切线方程3.1 若P(x0,y0)在圆x2+y2=r2上, 则以P为切点的圆的切线方程为:x0x+y0y=r23.2 若P(x0,y0)在圆x2+y2=r2外,则过P的切线方程可设为:y-y0=k(x-x0),利用待定系数 法求解。
说明:k为切线斜率,同时应考虑斜率不存在的情况.4 例题选讲:例1. 已知直线l:y=kx+1,圆C:(x-1)2+(y+1)2=12。
(1)试证明:不论k为何实数,直线l和圆C总有两个交点;(2)求直线l被圆C截得的最短弦长。
(1)证明 由消去y得(k2+1)x2-(2-4k)x-7=0,因为Δ=(4k-2)2+28(k2+1)>0,所以不论k为何实数,直线l和圆C总有两个交点.(2)解 设直线与圆交于A(x1,y1)、B(x2,y2)两点,则直线l被圆C截得的弦长|AB|=1+k2|x1-x2|=28-4k+11k21+k2=2 11-4k+31+k2,令t=4k+31+k2,则tk2-4k+(t-3)=0,当t=0时,k=-34,当t≠0时,因为k∈R,所以Δ=16-4t(t-3)≥0,解得-1≤t≤4,且t≠0,故t=4k+31+k2的最大值为4,此时|AB|最小为27。
初中数学直线与圆相切练习题(附答案)

初中数学直线与圆相切练习题一、单选题1.O 的半径为5,点A 在直线l 上,若5OA =,则直线l 与O 的位置关系是( )A.相离B.相切C.相交D.相切或相交2.已知O 和直线l 相交,圆心到直线l 的距离为10cm ,则O 的半径可能为( )A.11cmB.10cmC.9cmD.8cm3.如图,在平面直角坐标系中,半径为2的圆P 的圆心P 的坐标为(3,0)-,将圆P 沿x 轴的正方向平移,使得圆P 与y 轴相切,则平移的距离为( )A.1B.3C.5 D1或54.在Rt ABC △中,90C ∠=°,8cm AC =,10cm AB =,以C 为圆心,以9cm 长为直径的C 与直线AB 的位置关系为( )A.相交B.相离C.相切D.相离或相交5.已知A 在平面直角坐标系中,点A 的坐标为()7,0-,点B 的坐标为()7,4-,点C 的坐标为()12,0-,若A 的半径为5,则下列说法中不正确的是( )A.点B 在A 内B.点C 在A 上C. y 轴和A 相切D. x 轴和A 相交 6.圆的半径为5 cm ,圆心到一条直线的距离是7 cm,则这条直线与圆( )A.有两个公共点B.有一个公共点C.没有公共点D.公共点个数不定7.如图,直线l 与半径为10cm 的O 相交于,A B 两点,且与半径OC 垂直,垂足为H ,已知16cm AB =,若将直线l 平移使其与O 相切,则平移的距离为( )A.4cmB.6cmC.4cm 或14cmD.4cm 或16cm8.在ABC △中,90,4,5C AC AB ∠===°,以点C 为圆心,R 为半径作圆.若C 与边AB 只有一个公共点,则R 的取值范围是( ) A.125R = B.34R ≤≤ C.03R <<或4R > D.34R <≤或125R =9.在平面直角坐标系中,以点(3,2)为圆心,3为半径的圆,一定( )A.与x 轴相切,与y 轴相切B.与x 轴相切,与y 轴相交C.与x 轴相交,与y 轴相切D.与x 轴相交,与y 轴相交二、解答题10.在Rt ABC △中,90C ∠=︒,4cm,2cm AB BC ==,以C 为圆心,r 为半径的圆与AB 有何种位置关系?请你写出判断过程.(1) 1.5cm r =;(2)3cm r =;(3)2cm r =.三、填空题11.如图,已知P 的半径为2,圆心P 在抛物线2112y x =-上运动,当P 与x 轴相切时,圆心P 的坐标为 .12.如图,给定一个半径长为2的圆,圆心O 到水平直线l 的距离为d .即OM d =.我们把圆上到直线l 的距离等于1的点的个数记为m .如0d =时,l 为经过圆心O 的一条直线,此时圆上有4个到直线的距离等于1的点,即4m =,由此可知,当3d =时,m = .13.如图,ABC △的一边AB 是O 的直径,请你添加一个条件,使BC 是O 的切线,你所添加的条件为__________.14.如图,在△ABC 中,AB=AC,∠B=30°,以点A 为圆心,以3 cm 为半径作⊙A,当AB=__________cm 时,BC 与⊙A 相切.参考答案1.答案:D 解析:如图,连接OA ,若OA l ⊥,则直线l 与O 的位置关系是相切;若OA 不垂直于直线l ,则直线l 与O 的位置关系是相交.2.答案:A解析:O 和直线相交,∴圆心到直线的距离小于O 的半径 又圆心到直线l 的距离为10cm ,O ∴的半径大于10cm 故选A.3.答案:D解析:当圆P 在y 轴的左侧与y 轴相切时,平移的距离为321-=,当圆P 在y 轴的右侧与y 轴相切时,平移的距离为325+=.故选D.4.答案:B解析:∵8cm 10cm 90AC AB C ==∠=,,°, ∴226cm BC AB AC =-=,2118624(cm )22ABC S AC BC =⨯=⨯⨯=△, ∴AB 上的高为24210=4.8(cm)⨯÷,即圆心到直线的距离是4.8cm.∵ 4.5cm 4.8 4.5r =>,,∴C 与直线AB 相离,故选B.5.答案:C解析:如图,∵点A 的坐标为()7,0-,点B 的坐标为()7,4-,点C 的坐标为()12,0-, 5,45,75AC AB OA ∴==<=>∴点C 在A 上,点B 在A 内,x 轴和A 相交,y 轴和A 相离,故选C.6.答案:C解析:∵圆心到直线的距离7d =cm 圆的半径5r =cmd r ∴>∴圆与直线的位置关系为相离.没有交点.7.答案:D解析:,AB OC AH BH ⊥∴=1116822BH AB ∴==⨯=在Rt BOH △中,10OB =,6OH ∴=== 又将直线l 通过平移使直线l 与O 相切,∴直线l 垂直过C 点的直径,垂足为直径的两端点,∴当向下平移时,直线l 平移的距离1064cm =-=当向上平移时,直线l 平移的距离10616cm =+=故选D.8.答案:D解析:如图,过点C 作CD AB ⊥于点D.904,5ACB AC AB ∠===°,3BC ∴=.①如果以点C 为圆心,R 为半径的圆与斜边AB 相切,则CD R =.此时,CD AB AC BC ⋅=⋅125R CD ∴==. ②当34R <≤时,圆与边AB 也只有一个公共点.综上,34R <≤或125R =.9.答案:C解析:因为圆心到x 轴上的为2,到y 轴的距离为3,3r = 所以圆与与x 轴相交,与y 轴相切,故选C.10.答案:(1)90,4cm C AB ∠=︒=,2cm BC =AC ∴=设点C 到直线AB 的距离为d则根据直角三角形的面积公式可得112422d ⨯=⨯则24d ==1.5cm r =<,所以圆与直线AB 相离;(2)r ==,所以圆与直线AB 相切;(3)r =,所以圆与直线AB 相交.解析:11.答案:2)或(2)解析:解:P 与x 轴相切时,P 点纵坐标为2±当2y =时,21122x -=,解得6x =± 当2y =-时,21122x -=-,x 无解.故P 点坐标为2)或(2).12.答案:1解析:如图,当3d =时,O 到直线l 的距离为3,到直线1l 的距离为2,O的半径为2,O∴与直线1l相切,与直线l相离,此时圆上只有该切点与l的距离为1,即1m=.13.答案:90ABC∠︒=(答案不唯一)解析:当ABC△为直角三角形时,即90ABC∠︒=时,BC与圆相切, ∵AB是O的直径,90ABC∠︒= ,∴BC是O的切线.14.答案:6解析:如图,过点A作AD⊥BC于点D.∵AB=AC,∠B=30°,∴AD=12AB,即AB=2AD.又∵BC与⊙A相切,∴AD就是圆A的半径,∴AD=3cm,则AB=2AD=6cm. 故答案为:6.考点:切线的判定.。
与圆有关的动点问题.doc题

动点问题(4)------与圆有关的动点直线与圆相切1.如图,⊙O 的半径为1,圆心O 在正三角形的边AB 上沿图示方向移动,当⊙O 移动到与AC 边相切时,OA 的长是 .2.如图,已知⊙O 的半径为6cm ,射线PM 经过点O ,10cm OP ,射线PN 与⊙O 相切于点Q .A B ,两点同时从点P 出发,点A 以5cm/s 的速度沿射线PM 方向运动,点B 以4cm/s 的速度沿射线PN 方向运动.设运动时间为t s .(1)求PQ 的长; (2)当t 为何值时,直线AB 与⊙O 相切?3如图,ABC ∆中,090C ∠=,4AC =,3BC =.半径为1的圆的圆心P 以1个单位/s 的速度由点A 沿AC 方向在AC 上移动,设移动时间为t (单位:s ). (1)当t 为何值时,⊙P 与AB 相切;(2)作PD AC ⊥交AB 于点D ,如果⊙P 和线段BC 交于点E ,证明:当165t s=时,四边形PDBE 为平行四边形.4.(2012河北中考25)如图14,(50)(30).A B --,,,点C 在y 轴的正半轴上,CBO∠=45,CD AB ∥,90CDA = ∠.点P 从点(40)Q ,出发,沿x 轴向左以每秒1个单位长的速度运动,运动时间为t 秒.(1) 求点C 的坐标;(2) 当15BCP =∠时,求t 的值;(3) 以点P 为圆心,PC 为半径的P ⊙随点P 的运动而变化,当P ⊙与四边形ABCD 的边(或边所在的直线)相切时,求t 的值.5.如图,形如量角器的半圆O的直径DE=12cm,形如三角板的⊿ABC中,∠ACB=90°,∠ABC= 30°,BC=12cm。
半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC 上。
设运动时间为t (s),当t=0s时,半圆O在⊿ABC的左侧,OC=8cm。
(1)当t为何值时,⊿ABC的一边所在直线与半圆O所在的圆相切?(2)当⊿ABC的一边所在直线与半圆O所在的圆相切时,如果半圆O与直线DE围成的区域与⊿ABC 三边围成的区域有重叠部分,求重叠部分的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明直线与圆相切是一类常见题目,解决这类问题常用的方法有两种。
一、连半径,证垂直
若图形中已给出直线与圆的公共点,但未给出过点的半径,则可先连结过此点的半径,再证其与直线垂直。
例1如图(1)所示,在△ABC中,AB=AC,以AB为直径作圆交于BC于D,作DE⊥AC于E。
求证:DE为⊙O 的切线。
证明:连结OD
∵OB=OD
∴∠B=∠ODB
∵AB=AC
∴∠B=∠C
∴∠ODB=∠C
∵ DE⊥AC
∴∠C+∠CDE=90°
∴∠ODB+∠CDE=90°
∴∠ODE=90°,即DE⊥OD
∴DE是⊙O的切线。
例2如图(2)所示,AB是⊙O的直径,过A点作⊙O的切线,在切线上任取一点C,连结OC交⊙O于D,连结BD并延长交AC于E,求证:CD是△ADE外接圆的切线。
证明:取AE的中点F,连结FD。
∵AB为直径,
∴AD⊥BD
∵FD=FE(=FA)
∴∠FED=∠FDE
∵∠CDE=∠BDO=∠B
∠FEB+∠B=90°
∴∠FDE+∠CDE=90°
即FD⊥CD
∴CD是△ADE的外接圆的切线。
二、作垂线,证半径
若图形中未给出直线与圆的公共点,则需先过圆心作该直线的垂线,再证垂足到圆心的距离等于半径。
例3 如图(3)所示,已知AB是⊙O的直径,AC⊥L于C,BD⊥L于D,且AC+BD=AB。
求证:直线L与⊙O 相切。
证明:过O作OE⊥L于E。
∵AC⊥L,BD⊥L,
∴AC∥OE∥BD。
又AO=OB,∴CE=CD
从而OE为梯形ACDB的中位线。
∴OE=(AC+BD)=AB
即垂足E到圆心O的距离等于半径。
故直线L与⊙O相切。
