圆切线证明题
2016_中考数学圆切线的证明题题集
2016年中考数学圆切线的证明题1．已知：如图，AB是⊙O的直径，AD是弦，OC垂直AD于F交⊙O于E，连结DE、BE，且∠C=∠BED．（1）求证：AC是⊙O的切线；（2）若OA=10，AD=16，求AC的长．2．（本题12分）如图，已知CD是△ABC中AB边上的高，以CD为直径的⊙O分别交CA、CB于点E、F，点G是AD的中点．求证：GE是⊙O的切线．3、如图是⊙O的直径，∠A=30o,延长OB到D使BD=OB.(1)ABC是否是等边三角形说明理由.(2)求证：DC是⊙O的切线.4、如图，在△ABC中，AB=AC，D是BC中点，AE平分∠BAD交BC于点E，点O是AB上一点，⊙O过A、E两点, 交AD于点G，交AB于点F．（1）求证：BC与⊙O相切；（2）当∠BAC=120°时，求∠EFG的度数．CEDAFOB图8AODBCBACDEGO F第5题图5．（10分）如图，点D 在O ⊙的直径AB 的延长线上，点C 在O ⊙上，CD AC =，0120=∠ACD ， （1）求证：CD 是O ⊙的切线；（2）若O ⊙的半径为2，求图中阴影部分的面积.6.在Rt △ACB 中，∠C =90°，AC =3cm ，BC =4cm ，以BC 为直径作⊙O 交AB 于点D .（1）求线段AD 的长度；（2）点E 是线段AC 上的一点，试问当点E 在什么位置时，直线ED 与⊙O 相切请说明理由.7、如图，等腰三角形ABC 中，AC ＝BC ＝6，AB ＝8．以BC 为直径作⊙O 交AB 于点D ，交AC 于点G ，DF ⊥AC ，垂足为F ，交CB 的延长线于点E ． (1)求证：直线EF 是⊙O 的切线； (2)求sin ∠E 的值．8、如图，直线l 与⊙O 相交于A ，B 两点，且与半径OC 垂直，垂足为H ，已知AB =16厘米，4cos 5OBH ∠=． (1) 求⊙O 的半径；(2) 如果要将直线l 向下平移到与⊙O 相切的位置，平移的距离应是多少请说明理由．9．如图，⊙O 的直径AB=4，C 、D 为圆周上两点，且四边形OBCD 是菱形，过点D 的直线EF ∥AC ，交BA 、BC 的延长线于点E 、F ．（1）求证：EF 是⊙O 的切线； （2）求DE 的长．ODCB A （第7题图）ABO HClOFEDCB AMA D BN C oEF10、如图，已知矩形ABCD 内接于⊙O ，BD 为⊙O 直径,将△BCD 沿BD 所在的直线翻折后，得到点C 的对应点N 仍在⊙O 上,BN 交AD 与点M.若∠AMB=60°，⊙O 的半径是3cm.(1)求点O 到线段ND 的距离.(2)过点A 作BN 的平行线EF ，判断直线EF 与⊙O 的位置关系并说明理由.11． 如图，在⊙O 中，直径AB 垂直于弦CD ，垂足为E ，连接AC ，将△ACE 沿AC 翻折得到△ACF ，直线FC 与直线AB 相交于点G ．（1）直线FC 与⊙O 有何位置关系并说明理由； （2）若2OB BG ==，求CD 的长．12．如图，ABC △内接于O ，点D 在半径OB 的延长线上，30BCD A ∠=∠=°．（1）试判断直线CD 与O 的位置关系，并说明理由；（2）若O 的半径长为1，求由弧BC 、线段CD 和BD 所围成的阴影部分面积（结果保留π和根号）．13．(10分)已知，如图在矩形ABCD 中，点0在对角线AC 上，以 OA 长为半径的圆0与AD 、AC 分别交于点E 、F 。
专题 证明圆的切线的常用方法(六大题型)(解析版)
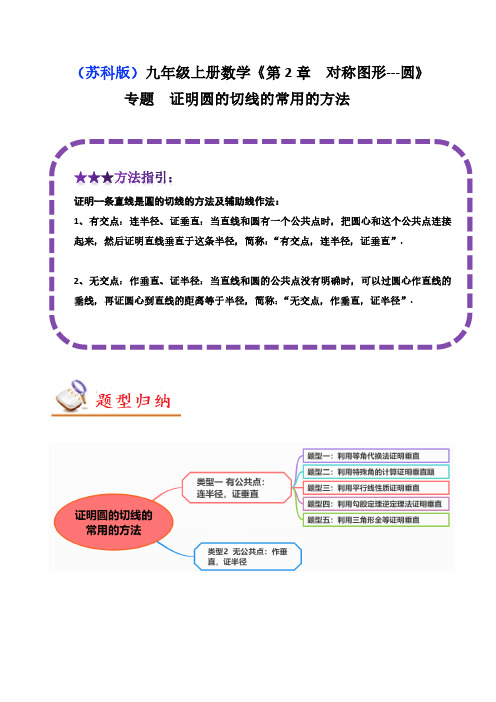
（苏科版）九年级上册数学《第2章对称图形---圆》专题证明圆的切线的常用的方法★★★方法指引：证明一条直线是圆的切线的方法及辅助线作法：1、有交点：连半径、证垂直：当直线和圆有一个公共点时，把圆心和这个公共点连接起来，然后证明直线垂直于这条半径，简称：“有交点，连半径，证垂直”.2、无交点：作垂直、证半径：当直线和圆的公共点没有明确时，可以过圆心作直线的垂线，再证圆心到直线的距离等于半径，简称：“无交点，作垂直，证半径”.类型一：有公共点：连半径，证垂直●●【典例一】（2022•雁塔区校级模拟）如图，AB 是⊙O 的直径，点D 在直径AB 上（D 与A ，B 不重合），CD ⊥AB ，且CD ＝AB ，连接CB ，与⊙O 交于点F ，在CD 上取一点E ，使得EF ＝EC ．求证：EF 是⊙O 的切线；【分析】连接OF ，根据垂直定义可得∠CDB ＝90°，从而可得∠B +∠C ＝90°，然后利用等腰三角形的性质可得∠B ＝∠OFB ，∠C ＝∠EFC ，从而可得∠OFB +∠EFC ＝90°，最后利用平角定义可得∠OFE ＝90°，即可解答；【解答】证明：连接OF ，∵CD ⊥AB ，∴∠CDB ＝90°，∴∠B +∠C ＝90°，∵OB ＝OF ，EF ＝EC ，∴∠B ＝∠OFB ，∠C ＝∠EFC，∴∠OFB+∠EFC＝90°，∴∠OFE＝180°﹣（∠OFB+∠EFC）＝90°，∵OF是⊙O的半径，∴EF是⊙O的切线：【点评】本题考查了切线的判定与性质，勾股定理，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．【变式1-1】（2022•澄城县三模）如图，AB是△ABC外接圆⊙O的直径，过⊙O外一点D作BC的平行线分别交AC，AB于点G，E，交⊙O于点F，连接DB，CF，∠BAC＝∠D．求证：BD是⊙O的切线；【分析】证明∠ABD＝90°，根据切线的判定可得BD与⊙O相切；【解答】证明：∵AB是⊙O的直径，∴∠ACB＝90°，∵DG∥BC，∴∠AGE＝∠ACB＝90°，∴∠A+∠AEG＝90°，又∵∠A＝∠D，∠AEG＝∠DEB，∴∠D+∠DEB＝90°，∴∠DBE＝90°，∴AB⊥BD，∵AB为直径，∴BD与⊙O相切；【点评】此题考查了切线的判定，垂径定理，解答本题需要我们熟练掌握切线的判定．【变式1-2】如图，AB是⊙O的直径，点C是圆上一点，CD⊥AB于点D，点E是圆外一点，CA平分∠ECD．求证：CE是⊙O的切线．【分析】利用切线的判定定理证明∠OCE＝90°即可得出结论．【解答】证明：∵CA平分∠ECD，∴∠ECA＝∠DCA．∵CD⊥AB，∴∠CAD+∠DCA＝90°，∴∠ECA+∠CAD＝90°．∵OA＝OC，∴∠CAD＝∠ACO，∴∠ECA+∠ACO＝90°，即∠OCE＝90°，∴OC⊥EC，∵OC是⊙O的半径，∴CE是⊙O的切线．【点评】本题主要考查了圆的切线的判定，熟练应用圆的切线的判定定理是解题的关键．【变式1-3】（2022秋•阳谷县校级期末）如图，△ABC内接于半圆，AB是直径，过A作直线MN，∠MAC＝∠ABC，D是弧AC的中点，连接BD交AC于G，过D作DE⊥AB于E，交AC于F．（1）求证：MN是半圆的切线．（2）求证：FD＝FG．【分析】（1）欲证明MN是半圆的切线，只需证得∠MAB＝90°，即MA⊥AB即可；（2）根据圆周角定理推论得到∠ACB＝90°，由DE⊥AB得到∠DEB＝90°，则∠1+∠5＝90°，∠3+∠4＝90°，又D是弧AC的中点，即弧CD＝弧DA，得到∠3＝∠5，于是∠1＝∠4，利用对顶角相等易得∠1＝∠2，则有FD＝FG．【解答】证明：（1）如图，∵AB是直径，∴∠ACB＝90°，∴∠CAB+∠ABC＝90°．又∵∠MAC＝∠ABC，∴∠MAC+∠CAB＝90°，即∠MAB＝90°，∴MA⊥AB．∴MN是半圆的切线．（2）∵AB为直径，∴∠ACB＝90°，而DE⊥AB，∴∠DEB＝90°，∴∠1+∠5＝90°，∠3+∠4＝90°，∵D是弧AC的中点，即弧CD＝弧DA，∴∠3＝∠5，∴∠1＝∠4，而∠2＝∠4，∴∠1＝∠2，∴FD＝FG．【点评】本题考查了切线的判定：经过半径的外端点，并且与半径垂直的直线是圆的切线．也考查了圆周角定理及其推论、三角形外角的性质以及等腰三角形的判定．【变式1-4】如图，AB为⊙O的直径，PD切⊙O于点C，与BA的延长线交于点D，DE⊥PO交PO延长线于点E，连接OC，PB，已知PB＝6，DB＝8，∠EDB＝∠EPB．（1）求证：PB是⊙O的切线；（2）求⊙O的半径．（3）连接BE，求BE的长．【分析】（1）由已知角相等及直角三角形的性质得到∠OBP为直角，即可得证；（2）在直角三角形PBD中，由PB与DB的长，利用勾股定理求出PD的长，由切线长定理得到PC＝PB ＝6，由PD﹣PC求出CD的长，在直角三角形OCD中，设OC＝r，则有OD＝8﹣r，利用勾股定理列出关于r的方程，求出方程的解得到r的值，即为圆的半径．（3）延长PB、DE相交于点F，证明△PED≌△PEF（ASA），由全等三角形的性质得出PD＝PF＝10，DE ＝EF，求出DF的长，则可得出答案．【解答】（1）证明：∵DE⊥PE，∴∠DEO＝90°，∵∠EDB＝∠EPB，∠BOE＝∠EDB+∠DEO，∠BOE＝∠EPB+∠OBP，∴∠OBP＝∠DEO＝90°，∴OB⊥PB，∴PB为⊙O的切线；（2）解：在Rt△PBD中，PB＝6，DB＝8，根据勾股定理得：PD=10，∵PD与PB都为⊙O的切线，∴PC＝PB＝6，∴DC＝PD﹣PC＝10﹣6＝4；在Rt△CDO中，设OC＝r，则有OD＝8﹣r，根据勾股定理得：（8﹣r）2＝r2+42，解得：r＝3，则圆的半径为3．（3）延长PB、DE相交于点F，∵PD与PB都为⊙O的切线，∴OP平分∠CPB，∴∠DPE＝∠FPE，∵PE⊥DF，∴∠PED＝∠PEF＝90°，又∵PE＝PE，∴△PED ≌△PEF （ASA ），∴PD ＝PF ＝10，DE ＝EF ，∴BF ＝PF ﹣PB ＝10﹣6＝4，在Rt △DBF 中，DF==∴BE =12DF =【点评】本题考查了切线的判定和性质，勾股定理，平行线的性质，全等三角形的判定和性质，熟练掌握性质定理是解题的关键．●●【典例二】 如图，△ABC 是直角三角形，点O 是线段AC 上的一点，以点O 为圆心，OA 为半径作圆．O 交线段AB 于点D ，作线段BD 的垂直平分线EF ，EF 交线段BC 于点．（1）若∠B ＝30°，求∠COD 的度数；（2）证明：ED 是⊙O 的切线．【分析】（1）根据三角形的内角和定理得到∠A ＝60°，根据等腰三角形的性质得到∠ODA ＝∠A ＝60°，于是得到∠COD ＝∠ODA +∠A ＝120°；（2）根据线段垂直平分线的性质得到∠EDB ＝∠B ＝30°，求得ED ⊥DO ，根据切线的判定定理即可得到结论．【解答】（1）解：∵∠C ＝90°，∠B ＝30°，∴∠A ＝60°，∵OD ＝OA，∴∠COD＝∠ODA+∠A＝120°；（2）证明：∵EF垂直平分BD，∴∠EDB＝∠B＝30°，∴∠EDO＝180°﹣∠EDB﹣∠ODA＝180°﹣30°﹣60°＝90°，∴ED⊥DO，∵OD是⊙O的半径，∴ED是⊙O的切线．【点评】本题考查了切线的判定，等腰三角形的性质，线段垂直平分线的性质，熟练掌握切线的判定定理是解题的关键．【变式2-1】如图，AB为⊙O的直径，点C，D在⊙O上，AC=CD=DB，DE⊥AC．求证：DE是⊙O的切线．【分析】连接OD，根据已知条件得到∠BOD=13×180°=60°，求得∠EAD=∠DAB=12∠BOD=30°，根据等腰三角形的性质得到∠ADO＝∠DAB＝30°，求得∠EDA＝60°，根据切线的判定定理即可得到结论．【解答】证明：连接OD，∵AC=CD=DB，∴∠BOD=13×180°=60°，∵CD=DB，∴∠EAD=∠DAB=12∠BOD=30°，∵OA＝OD，∴∠ADO＝∠DAB＝30°，∵DE⊥AC，∴∠E＝90°，∴∠EDA＝60°，∴∠EDO＝∠EDA+∠ADO＝90°，∴OD⊥DE，∵OD是⊙O的半径，∴DE是⊙O的切线．【点评】本题考查了切线的判定，等腰三角形的性质，正确的作出辅助线是解题的关键．【变式2-2】如图，AC是⊙O的直径，B在⊙O上，BD平分∠ABC交⊙O于点D，过点D作DE∥AC交BC的延长线于点E．求证：DE是⊙O的切线．【分析】连接OD，根据圆周角定理的推论得到∠ABC＝90°，根据角平分线的性质求出∠DBE＝45°，根据圆周角定理得到∠DOC，根据平行线的性质求出∠ODE＝90°，根据切线的判定定理证明结论；【解答】证明：连接OD，∵AC是⊙O的直径，∴∠ABC＝90°，∵BD平分∠ABC，∴∠DBE＝45°，∴∠DOC＝2∠DBE＝90°，∵DE∥AC，∴∠ODE＝∠DOC＝90°，∴DE是⊙O的切线；【点评】本题考查的是切线的判定定理、圆周角定理以及正方形的判定和性质，掌握经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键．【变式2-3】（2023•鼓楼区校级模拟）如图，在⊙O中，AB为⊙O的直径，AC为弦，OC＝4，∠OAC＝60°．（1）求∠AOC的度数；（2）在图（1）中，P为直径BA的延长线上一点，且S△PAC=PC为⊙O的切线；【分析】（1）根据等腰三角形中有一角为60度时是等边三角形得到△ACO是等边三角形，则∠AOC＝60°；（2）由等边三角形的性质以及勾股定理得出CD的长，再利用三角形外角的性质以及等腰三角形的性质得出∠PCA＝30°，进而得出答案；【解答】（1）解：在△OAC中，∵OA＝OC＝4，∠OAC＝60°，∴△OAC是等边三角形，∴∠AOC＝60°；（2）证明：过点C作CD⊥AO于点D，∵△AOC是等边三角形，CD⊥AO，∴AD＝DO=12OA＝2，∠ACO＝60°，∴CD∵S △PAC ＝∴12PA •CD ＝∴PA ＝4，∴PA ＝AC ，∴∠P ＝∠PCA =12∠OAC ＝30°，∴∠PCO ＝∠PCA +∠ACO ＝30°+60°＝90°，∴OC ⊥PC ，∵OC 是⊙O 的半径，∴PC 为⊙O 的切线．【点评】本题考查了等边三角形的判定和性质，切线的判定，熟练掌握相关的性质和判定是解决问题的关键．【变式2-4】（2023•门头沟区二模）如图，AB 是⊙O 直径，弦CD ⊥AB 于E ，点F 在CD 上，且AF ＝DF ，连接AD ，BC ．（1）求证：∠FAD ＝∠B（2）延长FA 到P ，使FP ＝FC ，作直线CP ．如果AF ∥BC ．求证：直线CP 为⊙O 的切线．【分析】（1）根据垂径定理、圆周角定理可得∠ACD ＝∠ACD ＝∠B ，根据等腰三角形的性质可得∠FAD＝∠FDA，进而可得∠FAD＝∠B；（2）根据平行线的性质以及三角形内角和定理可得∠FAB＝∠FAD＝∠FDA＝30°，进而得到∠CFP＝60°，再利用等边三角形的性质可得∠PCO＝60°+30°＝90°，由切线的判定方法可得结论．【解答】证明：（1）如图，连接AC，∵AB是⊙O直径，弦CD⊥AB，∴AC=AD，∴∠ACD＝∠ACD＝∠B，∵AF＝FD，∴∠FAD＝∠FDA，∴∠FAD＝∠B；（2）如图，连接OC，∵AF∥BC，∴∠FAB＝∠B，∴∠FAB＝∠FAD＝∠FDA，∵∠AED＝90°，∴∠FAB＝∠FAD＝∠FDA＝30°，∴∠CFP＝60°，∵FP＝FC，∴△CFP是等边三角形，∴∠PCF＝60°，∵OB＝OC，∴∠B＝∠OCB＝30°，∴∠OCD＝30°，∴∠PCO＝60°+30°＝90°，即OC⊥PC，∵OC是半径，∴PC是⊙O的切线．【点评】本题考查切线的判定，圆周角定理、平行线的性质以及三角形内角和定理，掌握切线的判定方法，圆周角定理是正确解答的前提．●●【典例三】如图，四边形ABCD 内接于⊙O ，AB 为⊙O 的直径，过点C 作CE ⊥AD 交AD 的延长线于点E ，延长EC ，AB 交于点F ，∠ECD ＝∠BCF ．求证：CE 为⊙O 的切线；【分析】连接OC ，BD ，可推出EF ∥BD ，进而可证CD =BC ，进而得出CE 为⊙O 的切线；【解答】证明：如图1，连接OC ，BD ，∵AB 是⊙O 的直径，∴∠ADB ＝90°，∵CE ⊥AE，∴∠E＝∠ADB，∴EF∥BD，∴∠ECD＝∠CDB，∠BCF＝∠CBD，∵∠ECD＝∠BCF，∴∠CDB＝∠CBD，∴CD=BC，∴半径OC⊥EF，∴CE为⊙O的切线；【点评】本题考查了圆周角定理及其推论，圆的切线判定，解决问题的关键是作合适的辅助线．【变式3-1】（2022秋•阿瓦提县校级期末）已知：AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使AB＝AC，连结AC，过点D作DE⊥AC，垂足为E．求证：DE为⊙O的切线．【分析】连接OD，根据OA＝OB，CD＝BD，得出OD∥AC，∠ODE＝∠CED，再根据DE⊥AC，即可证出OD⊥DE，从而得出答案．【解答】证明：如图，连接OD．∵AB是⊙O的直径，∴∠ADB＝90°，∴CD＝BD，∵OA＝OB，∴OD∥AC．∴∠ODE＝∠CED．∵DE⊥AC，∴∠CED＝90°．∴∠ODE＝90°，∴OD⊥DE，∵OD是⊙O的半径，∴DE是⊙O的切线．【点评】本题考查了切线的判定与性质，解决本题的关键是掌握圆周角定理的推论、线段垂直平分线的性质以及等边三角形的判定，是一道常考题型．【变式3-2】已知，如图，在△ABC中，BC＝AC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E．（1）求证：点D是AB的中点；（2）判断DE与⊙O的位置关系，并证明你的结论．【分析】（1）连接CD，如图，根据圆周角定理，由BC为直径得到∠BDC＝90°，然后根据等腰三角形的性质得AD＝BD；（2）连接OD，先得到OD为△ABC的中位线，再根据三角形中位线性质得OD∥AC，而DE⊥AC，则DE⊥OD，然后根据切线的判定定理可得DE为⊙O的切线．【解答】（1）证明：连接CD，如图，∵BC为直径，∴∠BDC＝90°，∴CD⊥AB，∵AC＝BC，∴AD＝BD，即点D是AB的中点；（2）解：DE与⊙O相切．理由如下：连接OD，∵AD＝BD，OC＝OB，∴OD为△ABC的中位线，∴OD∥AC，而DE⊥AC，∴DE⊥OD，∴DE为⊙O的切线．【点评】本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．【变式3-3】如图，已知点E在△ABC的边AB上，∠C＝90°，∠BAC的平分线交BC于点D，且D在以AE为直径的⊙O上．（1）求证：BC是⊙O的切线；（2）已知∠B＝30°，CD＝4，求线段AB的长．【分析】（1）连接OD，根据角平分线的定义得到∠BAD＝∠CAD，而∠OAD＝∠ODA，则∠ODA＝∠CAD，于是判断OD∥AC，由于∠C＝90°，所以∠ODB＝90°，然后根据切线的判定定理即可得到结论；（2）由∠B＝30°得到∠BAC＝60°，则∠CAD＝30°，在Rt△ADC中，根据含30度的直角三角形三边的关系得到AC＝Rt△ABC中，根据含30度的直角三角形三边的关系可得到AB＝【解答】（1）证明：连接OD，如图，∵∠BAC的平分线交BC于点D，∴∠BAD＝∠CAD，∵OA＝OD，∴∠OAD＝∠ODA，∴∠ODA＝∠CAD，∴OD∥AC，∵∠C＝90°，∴∠ODB＝90°，∴OD⊥BC，∴BC是⊙O的切线；（2）解：∵∠B＝30°，∴∠BAC＝60°，∴∠CAD＝30°，在Rt△ADC中，DC＝4，∴AC=＝在Rt△ABC中，∠B＝30°，∴AB＝2AC＝【点评】本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了含30度的直角三角形三边的关系．【变式3-4】如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD，垂足为E，DA平分∠BDE．（1）求证：AE是⊙O的切线；（2）若∠DBC＝30°，DE＝1cm，求BD的长．【分析】（1）连接OA，根据角之间的互余关系可得∠OAE＝∠DEA＝90°，故AE⊥OA，即AE是⊙O的切线；（2）根据圆周角定理，可得在Rt△AED中，∠AED＝90°，∠EAD＝30°，有AD＝2DE；在Rt△ABD中，∠BAD＝90°，∠ABD＝30°，有BD＝2AD＝4DE，即可得出答案．【解答】（1）证明：连接OA，∵DA平分∠BDE，∴∠BDA＝∠EDA．∵OA＝OD，∴∠ODA＝∠OAD，∴∠OAD＝∠EDA，∴OA∥CE．∵AE⊥CE，∴AE⊥OA．∴AE是⊙O的切线．（2）解：∵BD是直径，∴∠BCD＝∠BAD＝90°．∵∠DBC＝30°，∠BDC＝60°，∴∠BDE＝120°．∵DA平分∠BDE，∴∠BDA＝∠EDA＝60°．∴∠ABD＝∠EAD＝30°．∵在Rt△AED中，∠AED＝90°，∠EAD＝30°，∴AD＝2DE．∵在Rt△ABD中，∠BAD＝90°，∠ABD＝30°，∴BD＝2AD＝4DE．∵DE的长是1cm，∴BD的长是4cm．【点评】此题主要考查了切线的判定，角平分线的性质，含30°的直角三角形的性质，勾股定理，矩形的判定和性质，构造出直角三角形是解本题的关键，是一道中等难度的中考常考题．●●【典例四】（2022•城关区一模）如图，C是⊙O上一点，点P在直径AB的延长线上，⊙O的半径为6，PB=4，PC=8．求证：PC是⊙O的切线；【分析】可以证明OC2+PC2=OP2得△OCP是直角三角形，即OC⊥PC，PC是⊙O的切线；【解答】解：如图，连接OC、BC，∵⊙O的半径为6，PB=4，PC=8．∴OC=OB=6，OP=OB+BP=6+4=10，∴OC2+PC2=62+82=100，OP2=102=100，∴OC2+PC2=OP2，∴△OCP是直角三角形，∴OC⊥PC，∴PC是⊙O的切线；【点评】本题考查圆的切线的判定和勾股定理逆定理，利用勾股定理的逆定理证明垂直是解决问题的关键．【变式4-1】如图，AD, BD是⊙O的弦，AD⊥BD，且BD=2AD=8 ,点C是BD的延长线上的一点，CD=2，求证：AC是⊙O的切线.【分析】先由勾股定理的逆定理证明垂直，再由切线的判断进行解答即可.【解答】证明:连接AB，∵AD⊥BD，且BD=2AD=8 ，∴AB为直径，AB2 =82+42 =80，∵CD=2，AD=4 ，∴AC2 =22 ＋42=20，∵CD＝2，BD=8,∴BC=102=100，∴AC2+AB2=CB2，∴∠BAC=90° ，∴AC是⊙O的切线【点评】本题考查切线的判定，圆周角定理的推论，勾股定理的逆定理，解题关键是作出辅助线构造直角三角形.【变式4-2】如图，AD，BD是⊙O的弦，AD⊥BD，且BD＝2AD＝8，点C是BD的延长线上的一点，CD＝2，求证：AC是⊙O的切线．【分析】先根据圆周角定理得到AB为⊙O的直径，再利用勾股定理计算出AB、AC，接着利用勾股定理的逆定理证明△ABC为直角三角形，∠BAC＝90°，所以AC⊥AB，然后根据切线的判定定理得到结论．【解答】证明：∵AD⊥BD，∴∠ADB＝90°，∴AB为⊙O的直径，∵BD ＝2AD ＝8，∴AD ＝4，在Rt △ADB 中，AB 2＝AD 2+BD 2＝42+82＝80，在Rt △ADC 中，AC 2＝AD 2+CD 2＝42+22＝20，∵BC 2＝（2+8）2＝10，∴AC 2+AB 2＝BC 2，∴△ABC 为直角三角形，∠BAC ＝90°，∴AC ⊥AB ，∵AB 为直径，∴AC 是⊙O 的切线．【点评】本题考查了切线的判定：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了圆周角定理、勾股定理和勾股定理的逆定理．●●【典例五】（2022•鄞州区校级开学）如图，AB 为⊙O 的直径，点C 和点D 是⊙O 上的两点，连接BC ，DC ，BC ＝CD ，CE ⊥DA 交DA 的延长线于点E ．求证：CE 是⊙O 的切线；【分析】连接OD ，OC ，证得△COD ≌△COB ，可得∠OCD ＝∠BCO ，从而得到∠ADC ＝∠DCO ，进而得到DA ∥CO ，利用切线的判定定理即可求证；【解答】证明：连接OD ，OC，如图，在△COD和△COB中，OD=OBOC=OC，CD=CB∴△COD≌△COB（SSS），∴∠OCD＝∠BCO，∵CO＝BO，∴∠B＝∠BCO，∵∠B＝∠ADC，∴∠ADC＝∠DCO．∴DA∥CO，∴∠E+∠ECO＝180°．∵CE⊥EA，∴∠E＝90°．∴∠ECO＝90°，∴EC⊥CO，∵CO是⊙O的半径，∴EC是⊙O的切线；【点评】本题主要考查了切线的判定，圆周角定理等知识，熟练掌握切线的判定，相似三角形的判定和性质，圆周角定理等知识是解题的关键．【变式5-1】如图，已知AB是⊙O的直径，BC⊥AB，连接OC，弦AD∥OC，直线CD交BA的延长线于点E．求证：CD是⊙O的切线；【分析】连接OD，利用SAS得到三角形COD与三角形COB全等，利用全等三角形的对应角相等得到∠ODC 为直角，即可得证；【解答】证明：如图，连接OD．∵AD∥OC，∴∠DAO＝∠COB，∠ADO＝∠COD，又∵OA＝OD，∴∠DAO＝∠ADO，∴∠COD＝∠COB，在△COD和△COB中，OC=OC∠COD=∠COB，OD=OB∴△COD≌△COB（SAS），∴∠CDO＝∠CBO＝90°，∵OD是⊙O的半径，∴CD是⊙O的切线；【点评】此题考查了切线的判定和性质，以及全等三角形的判定与性质，熟练掌握各自的性质是解本题的关键．【变式5-2】（2022秋•新抚区期末）如图，AB为⊙O的直径，四边形OBCD是矩形，连接AD，延长AD 交⊙O于E，连接CE．求证：CE为⊙O的切线．【分析】连接OC、BE，根据矩形性质和圆半径相等，推出∠CDE＝∠AEO，进而得到OP＝CP，然后根据OB∥CD，可以推出∠COE＝∠BOC，最后通过证明△BOC≌△EOC即可求解．【解答】证明：如图：连接OC、BE，OE，CD交于点P，∵四边形OBCD是矩形，∴OB∥CD，∠OBC＝90°，OB＝CD，∵OB∥CD，∴∠A＝∠CDE，∵在⊙O中，OA＝OB＝OE，∴OE＝CD，∵OA＝OE，∴∠A＝∠AEO，∴∠CDE＝∠AEO，∴DP＝PE，∵OE＝CD，∴OP＝CP，∴∠COE＝∠DCO，∵OB∥CD，∴∠DCO＝∠BOC，∴∠COE＝∠BOC，在△BOC和△EOC中，OB=OECO=CO，∠BOC=∠COE∴△BOC≌△EOC（SAS），∴∠CEO＝∠OBC＝90°，∴CE⊥OE，又∵OE为⊙O的半径，∴CE为⊙O的切线．【点评】本题考查圆周角定理，全等三角形的判定和性质，矩形的性质等众多知识点，熟悉掌握以上知识点是解题关键．【变式5-3】（2022•建邺区二模）如图，四边形ABCD是菱形，以AB为直径作⊙O，交CB于点F，点E在CD上，且CE＝CF，连接AE．（1）求证：AE是⊙O的切线；（2）连接AC交⊙O于点P，若AP BF＝1，求⊙O的半径．【分析】（1）连接AF，根据菱形的性质得到∠ACF＝∠ACE，根据全等三角形的性质得到∠AFC＝∠AEC，推出OA⊥AE，根据切线的判定定理即可得到结论；（2）连接BP，根据圆周角定理得到∠APB＝90°，求得AC＝2AP＝【解答】（1）证明：连接AF，∵四边形ABCD为菱形，∴∠ACF＝∠ACE，在△ACF与△ACE中，CF=CE∠ACF=∠ACEAC=AC，∴△ACF≌△ACE（SAS），∴∠AFC＝∠AEC，∵AB是⊙O的直径，∴∠AFB＝∠AFC＝90°，∴∠AEC＝90°，∵AB∥DC，∴∠BAE+∠AEC＝90°，∴∠BAE＝90°，∴OA⊥AE，∵OA是⊙O的半径，∴AE是⊙O的切线；（2）解：连接BP，∵AB是⊙O的直径，∴∠APB＝90°，∵AB＝CB，AP=∴AC＝2AP＝设⊙O的半径为R，∵AC2﹣CF2＝AF2，AB2﹣BF2＝AF2，∴2−(2R−1)2=(2R)2−12，∴R=32（负值舍去），∴⊙O的半径为3 2．【点评】本题考查了切线的判定和性质，圆周角定理，菱形的性质，三角形全等的性质和判定，勾股定理等知识，解答本题的关键是根据勾股定理列方程解决问题．类型二：无公共点：作垂直，证半径●●【典例六】如图，△ABC为等腰三角形，O是底边BC的中点，腰AB与⊙O相切于点D．求证：AC是⊙O的切线．【分析】过点O作OE⊥AC于点E，连接OD，OA，根据切线的性质得出AB⊥OD，根据等腰三角形三线合一的性质得出AO是∠BAC的平分线，根据角平分线的性质得出OE=OD，从而证得结论．【解答】证明：过点O作OE⊥AC于点E，连接OD，OA，∵AB与⊙O相切于点D，∴AB⊥OD，∵△ABC为等腰三角形，O是底边BC的中点，∴AO是∠BAC的平分线，∴OE=OD，即OE是⊙O的半径，∵圆心到直线的距离等于半径，∴AC是⊙O的切线．【点评】本题考查了切线的判定和性质，等腰三角形的性质，角平分线的性质，熟练掌握性质定理是解题的关键．【变式6-1】如图，O为正方形ABCD对角线AC上一点，以O为圆心，OA长为半径的⊙O与BC相切于点M．求证：CD与⊙O相切．【分析】利用正方形的性质得出AC平分角∠BCD，再利用角平分线的性质得出OM＝ON，即可得出答案．【解答】证明：如图所示，连接OM，过点O作ON⊥CD于点N，∵⊙O与BC相切于点M，∴OM⊥BC，又∵ON⊥CD，O为正方形ABCD对角线AC上一点，∴OM＝ON，∴ON为⊙O的半径，∴CD与⊙O相切．【点评】此题主要考查了正方形的性质以及角平分线的性质，得出OM＝ON是解题关键．【变式6-2】如图，OC平分∠AOB，D是OC上任意一点，⊙D和OA相切于点E，连接CE．（1）求证：OB与⊙D相切；（2）若OE＝4，⊙D的半径为3，求CE的长．【分析】（1）过点D作DF⊥OB于点F，先由切线的性质得DE⊥OA，则由角平分线的性质得DF＝DE，即可证得结论；（2）过E作EG⊥OD于G，先由勾股定理求出OD＝5，再由面积法求出EG=125，然后由勾股定理求出DG=95，最后由勾股定理求出CE即可．【解答】（1）证明：连接DE，过点D作DF⊥OB于点F，如图所示：∵⊙D与OA相切于点E，∴DE⊥OA，∵OC平分∠AOB，∴DF＝DE，又∵DF⊥OB，∴OB与⊙D相切；（2）解：过E作EG⊥OD于G，如图所示：由（1）得：DE⊥OA，∴∠OED＝90°，∵OE＝4，DE＝3，∴OD=5，∵EG⊥OD，∴12OD×EG=12OE×DE，∴EG=OE×DEOD=4×35=125，∴DG===9 5，∴CG＝CD+DG＝3+95=245，∴CE=【点评】此题考查了切线的判定与性质、勾股定理以及角平分线的性质等知识，解题的关键是准确作出辅助线．【变式6-3】如图，AB是⊙O的直径，AM，BN分别切⊙O于点A，B，CD交AM，BN于点D，C，DO平分∠ADC．（1）求证：CD是⊙O的切线；（2）若AD＝4，BC＝9，求⊙O的半径R．【分析】（1）过O点作OE⊥CD于点E，通过角平分线的性质得出OE＝OA即可证得结论．（2）过点D作DF⊥BC于点F，根据切线的性质可得出DC的长度，继而在Rt△DFC中利用勾股定理可得出DF的长，继而可得出半径．【解答】（1）证明：过O点作OE⊥CD于点E，∵AM切⊙O于点A，∴OA⊥AD，又∵DO平分∠ADC，∴OE＝OA，∵OA为⊙O的半径，∴OE是⊙O的半径，且OE⊥DC，∴CD是⊙O的切线．（2）解：过点D作DF⊥BC于点F，∵AM，BN分别切⊙O于点A，B，∴AB⊥AD，AB⊥BC，∴四边形ABFD是矩形，∴AD＝BF，AB＝DF，又∵AD＝4，BC＝9，∴FC＝9﹣4＝5，∵AM，BN，DC分别切⊙O于点A，B，E，∴DA＝DE，CB＝CE，∴DC＝AD+BC＝4+9＝13，在Rt△DFC中，DC2＝DF2+FC2，∴DF=12，∴AB＝12，∴⊙O的半径R是6．【点评】此题考查了切线的性质、角平分线的性质及勾股定理的知识，证明第一问关键是掌握切线的判定定理，解答第二问关键是熟练切线的性质．【变式6-4】（2022秋•清原县期末）如图，在△ABC中，∠ACB＝90°，点D是AB边的中点，点O在AC边上，⊙O 经过点C 且与AB 边相切于点E ，∠FAC =12∠BDC ．（1）求证：AF 是⊙O 的切线；（2）若BC ＝6，AB ＝10，求⊙O 的半径长．【分析】（1）作OH ⊥FA ，垂足为点H ，连接OE ，证明AC 是∠FAB 的平分线，进而根据OH ＝OE ，OE ⊥AB ，可得AF 是⊙O 的切线；（2）勾股定理得出AC ，设⊙O 的半径为r ，则OC ＝OE ＝r ，进而根据切线的性质，在Rt △OEA 中，勾股定理即可求解．【解答】（1）证明：如图，作OH ⊥FA ，垂足为点H ，连接OE ，∵∠ACB ＝90°，D 是AB 的中点，∴CD =AD =12AB ，∴∠CAD ＝∠ACD ，∵∠BDC ＝∠CAD +∠ACD ＝2∠CAD ，又∵∠FAC =12∠BDC ，∴∠FAC ＝∠CAD ，即AC 是∠FAB 的平分线，∵点O 在AC 上，⊙O 与AB 相切于点E ，∴OE ⊥AB ，且OE 是⊙O 的半径，∴OH ＝OE ，OH 是⊙O 的半径，∴AF 是⊙O 的切线；（2）解：如图，在△ABC中，∠ACB＝90°，BC＝6，AB＝10，∴AC==8，∵BE，BC是⊙O的切线，∴BC＝BE＝6，∴AE＝10﹣6＝4设⊙O的半径为r，则OC＝OE＝r，在Rt△OEA中，由勾股定理得：OE2+AE2＝OA2，∴16+r2＝（8﹣r）2，∴r＝3．∴⊙O的半径长为3．【点评】本题考查了切线的性质与判定，勾股定理，熟练掌握切线的性质与判定是解题的关键．1.如图，已知AB是⊙O的直径，AB＝BE，点P在BA的延长线上，连接AE交⊙O于点D，过点D作PC⊥BE垂足为点C．求证：PC与⊙O相切；【分析】连接OD，根据等腰三角形的性质得到∠BAE＝∠BEA，∠BAE＝∠ODA，等量代换得到∠ODA＝∠BEA，证明OD∥BE，根据平行线的性质得到PC⊥OD，根据切线的判定定理证明结论；【解答】证明：连接OD，∵AB＝BE，∴∠BAE＝∠BEA，∵OA＝OD，∴∠BAE＝∠ODA，∴∠ODA＝∠BEA，∴OD∥BE，∵PC⊥BE，∴PC⊥OD，∵OD是⊙O的半径，∴PC与⊙O相切；【点评】本题考查的是切线的判定、解直角三角形，掌握经过半径的外端且垂直于这条半径的直线是圆的切线是解题的关键．2．如图，△ABC是⊙O的内接三角形，AC是⊙O的直径，点D是BC的中点，DE∥BC交AC的延长线于点E．（1）求证：直线DE与⊙O相切；（2）若⊙O的直径是10，∠A＝45°，求CE的长．【分析】（1）连接OD，如图，先利用垂径定理得到OD⊥BC，再根据平行线的性质得到OD⊥DE，然后根据切线的判定方法得到结论；（2）先根据圆周角定理得到∠B＝90°，则∠ACB＝45°，再根据平行线的性质得到∠E＝45°，则可判断△ODE 为等腰直角三角形，于是可求出OE，然后计算OE﹣OC即可．【解答】（1）证明：连接OD，如图，∵点D是BC的中点，∴OD⊥BC，∵DE∥BC，∴OD⊥DE，∴直线DE与⊙O相切；（2）解：∵AC是⊙O的直径，∴∠B＝90°，∵∠A＝45°，∴∠ACB＝45°，∵BC∥DE，∴∠E＝45°，而∠ODE＝90°，∴△ODE为等腰直角三角形，∴OE=＝∴CE＝OE﹣OC＝5．【点评】本题考查了切线的性质与判定：圆的切线垂直于经过切点的半径．也考查了垂径定理、圆周角定理和等腰直角三角形的性质．3．（2023•东城区校级模拟）如图，⊙O的半径OC与弦AB垂直于点D，连接BC，OB．（1）求证：2∠ABC+∠OBA＝90°；（2）分别延长BO、CO交⊙O于点E、F，连接AF，交BE于G，过点A作AM⊥BC，交BC延长线于点M，若G是AF的中点，求证：AM是⊙O的切线．【分析】（1）先根据垂径定理得到AC=BC，再根据圆周角定理得到∠BOC＝2∠ABC，然后利用互余关系得∠BOD+∠OBD＝90°，从而得到结论；（2）如图，连接OA，根据垂径定理得到BE⊥AF，再根据圆周角定理得到∠CAF＝90°，则可判断BE ∥AC，所以∠ABE＝∠BAC，接着证明∠BAO＝∠CBA得到OA∥BC，根据平行线的性质得到AM⊥OA，然后根据切线的判断方法得到结论．【解答】证明：（1）∵OD⊥AB，∴AC=BC，∠ODB＝90°，∴∠BOC＝2∠ABC，∵∠BOD+∠OBD＝90°，∴2∠ABC+∠OBA＝90°；（2）如图，连接OA，∵G是AF的中点，∴BE⊥AF，∵CF为直径，∴∠CAF＝90°，∴CA⊥AF，∴BE∥AC，∴∠ABE＝∠BAC，∴AC=BC，∴∠CAB＝∠CBA，∵OA＝OB，∴∠BAO＝∠ABO，∴∠BAO＝∠CBA，∴OA∥BC，∵AM⊥BC，∴AM⊥OA，而OA为⊙O的半径，∴AM是⊙O的切线．【点评】本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了圆周角定理、垂径定理．4．（2022•思明区校级二模）如图，四边形ABCD是⊙O的内接四边形，AC是⊙O直径，BE∥AD交DC 延长线于点E，若BC平分∠ACE．（1）求证：BE是⊙O的切线；（2）若BE＝3，CD＝2，求⊙O的半径．【分析】（1）连接OB，由条件可以证明OB∥DE，从而证明OB⊥BE；（2）由垂径定理求出AD长，从而由勾股定理可求AC长．【解答】（1）证明：连接OB，∵″OB＝OC，∴∠OBC＝∠OCB，∵∠BCE＝∠OCB，∴∠OBC＝∠BCE，∴OB∥DE，∵AC是⊙O直径，∴AD⊥DE，∵BE∥AD，∴BE⊥DE，∴OB⊥BE，∵OB是⊙O半径，∴BE是⊙O切线；（2）解：延长BO交AD于F，∵∠D＝∠DEB＝∠EBF＝90°，∴四边形BEDF是矩形，∴BF⊥AD，DF＝BE＝3，∴AD＝2DF＝6，∵AC2＝AD2+CD2，∴AC2＝62+22＝40，∴AC＝∴⊙O【点评】本题考查切线的判定，矩形的判定和性质，垂径定理，勾股定理，用到的知识点较多，关键是熟练掌握知识点，并能灵活应用．5．（2023•封开县一模）如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过点D作EF⊥AC于点E，交AB的延长线于点F．（1）求证：EF是⊙O的切线；（2）当AB＝5，BC＝6时，求DE的长．【分析】（1）连接OD，由AC＝AB，根据等边对等角得到一对角相等，再由OD＝OB，根据等边对等角得到又一对角相等，等量代换可得一对同位角相等，根据同位角相等两直线平行可得OD与AC平行，又EF垂直于AC，根据垂直于两平行线中的一条，与另一条也垂直，得到EF与OD也垂直，可得EF为圆O的切线；（2）连接AD，由AB为圆的直径，根据直径所对的圆周角为直角可得∠ADB＝90°，即AD与BC垂直，又AC＝AB，根据三线合一得到D为BC中点，由BC求出CD的长，再由AC的长，利用勾股定理求出AD的长，三角形ACD的面积有两种求法，AC乘以DE除以2，或CD乘以AD除以2，列出两个关系式，两关系式相等可求出DE的长．【解答】（1）证明：连接OD，∵AB＝AC，∴∠C＝∠OBD，∵OD＝OB，∴∠1＝∠OBD，∴∠1＝∠C，∴OD∥AC，∵EF⊥AC，∴EF⊥OD，∴EF是⊙O的切线；（2）连接AD，∵AB为⊙O的直径，∴∠ADB＝90°，又∵AB＝AC，且BC＝6，∴CD＝BD=12BC＝3，在Rt△ACD中，AC＝AB＝5，CD＝3，根据勾股定理得：AD=4，又S△ACD =12AC•ED=12AD•CD，即12×5×ED=12×4×3，∴ED=12 5．【点评】此题考查了等腰三角形的性质，圆周角定理，平行线的性质，勾股定理，三角形面积的求法，以及切线的判定，其中证明切线的方法为：有点连接圆心与此点，证垂直；无点过圆心作垂线，证明垂线段长等于圆的半径．本题利用的是第一种方法．6．（2023•宁德模拟）如图，OM 为⊙O 的半径，且OM ＝3，点G 为OM 的中点，过点G 作AB ⊥OM 交⊙O 于点A ，B ，点D 在优弧AB 上运动，将AB 沿AD 方向平移得到DC ；连接BD ，BC ．（1）求∠ADB 的度数；（2）如图2，当点D 在MO 延长线上时，求证：BC 是⊙O 的切线．【分析】（1）连接AO ，BO ，先根据特殊角的正弦值可得∠OAG ＝30°，再根据等腰三角形的性质可得∠OAG ＝∠OBG ＝30°，从而可得∠AOB ＝120°，然后根据圆周角定理即可得；（2）连接AO ，BO ，CO ，先证出四边形ABCD 是平行四边形，再根据等边三角形的判定与性质可得AB ＝AD ，根据菱形的判定可得四边形ABCD 是菱形，根据菱形的性质可得CB ＝CD ，然后根据SSS 定理证出△COB ≌△COD ，根据全等三角形的性质可得∠OBC ＝∠ODC ＝90°，最后根据圆的切线的判定即可得证．【解答】（1）解：如图1，连接AO ，BO ．∵点G 为OM 的中点，且OM ＝3，∴OG =12OM =32，OA ＝OB ＝OM ＝3，∵AB ⊥OM ，在Rt △AOG 中，OG =12OA ．∴∠OAG ＝30°，又∵OA ＝OB ，∴∠OAG＝∠OBG＝30°，∴∠AOB＝120°，∴∠ADB=12∠AOB=60°．（2）证明：如图2，连接AO，BO，CO，由平移得：AB＝DC，AB∥DC，∴四边形ABCD是平行四边形，∵OM⊥AB，点D在MO延长线上，∴DM⊥CD，∵OA＝OB，AB⊥OM，∴AG＝BG，∴DM垂直平分AB，∴AD＝BD，∵∠ADB＝60°，∴△ABD为等边三角形，∴AB＝AD，∴平行四边形ABCD是菱形，∴CB＝CD，在△COB和△COD中，CB=CDOB=ODOC=OC，∴△COB≌△COD（SSS），∴∠OBC＝∠ODC＝90°，又∵OB是⊙O的半径，。
圆切线练习题(含答案)
圆切线练习题(含答案)XXX∠OAD，又∠OAD＝90°，∴∠XXX°。
又因为CD与半径OD重合，∴CD垂直于过切点D的半径，即CD是⊙O的切线。
例5.证明：由点悟可知，须证OD＝OA。
XXX是⊙O的直径，∴∠OAB＝90°，又∠XXX°，因此O、B、D三点共线。
OBD是直角三角形，∴OD＝OB×sin∠OBD＝r×sin∠OAB＝OA。
又因为OD是⊙O的半径，∴OD＝r。
OA＝r，即AC与⊙O相切。
例6.证明：如图所示。
OA⊥OB，∴∠XXX°，又∠OAD＝∠DPB，∴∠DPB＝90°。
CD是⊙O的切线，∴PC＝CD。
例7.解：如图所示。
O是内心，∴∠BOC＝2∠A＝140°。
答案：∠BOC＝140°。
题目：证明在一个圆中，若一条直径的一端点与圆上一点相连，且与该点相连的两条切线分别与直径所在直线交于不同点，则这两个交点和圆上的该点构成一个等腰三角形。
证明：连接直径的另一端点和圆上的该点，得到三角形ACD。
由于OA=OD，所以∠ODA=∠OAD，从而∠COB=∠COD。
又因为OD=OB，所以三角形COB≌三角形COD，从而∠B=∠XXX。
由于BC是切线，而AB是直径，所以∠B=90°，∠ODC=90°，因此CD是圆的切线。
在证明中，我们先利用“切线的性质定理”和“全等三角形”的基本图形，构造辅助线OD。
然后利用切线的判定定理，得到CD是圆的切线。
这样就证明了∠COB=∠COD和CD是圆的切线。
接下来，我们连接直径的另一端点和圆上的该点，得到三角形ACD。
由于OA=OD，所以∠ODA=∠OAD，从而∠COB=∠COD。
又因为OD=OB，所以三角形COB≌三角形COD，从而∠B=∠XXX。
由于BC是切线，而AB是直径，所以∠B=90°，∠ODC=90°，因此CD是圆的切线。
2022年中考数学大题圆证明切线的两种常用方法及专项练习题汇总
2022中考数学圆综合大题证明切线的两种常用方法类型1直线与圆有交点方法归纳：直线过圆上某一点，证明直线是圆的切线时，只需“连半径，证垂直，得切线”．“证垂直”时通常利用圆中的关系得到90°的角，如直径所对的圆周角等于90°等．【例1】如图，AB＝AC，AB是⊙O的直径，⊙O交BC于D，DM⊥AC于M.求证：DM与⊙O相切．1．(朝阳中考)如图，AB是⊙O的弦，OA⊥OD，AB，OD交于点C，且CD＝BD.(1)判断BD与⊙O的位置关系，并证明你的结论；(2)当OA＝3，OC＝1时，求线段BD的长．2．(德州中考)如图，已知⊙O的半径为1，DE是⊙O的直径，过D作⊙O的切线，C是AD的中点，AE交⊙O于B点，四边形BCOE是平行四边形．(1)求AD的长；(2)BC是⊙O的切线吗？若是，给出证明，若不是，说明理由．3．(毕节中考)如图，以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D为BE的下半圆弧的中点，连接AD交BC于F，AC＝FC.(1)求证：AC是⊙O的切线；(2)已知圆的半径R＝5，EF＝3，求DF的长．类型2不确定直线与圆是否有公共点方法归纳：直线与圆没有已知的公共点时，通常“作垂直，证半径，得切线”．证明垂线段的长等于半径常用的方法是利用三角形全等或者利用角平分线上的点到角的两边的距离相等．【例2】如图，AB＝AC，D为BC中点，⊙D与AB切于E点．求证：AC与⊙D相切．4．如图，O为正方形ABCD对角线AC上一点，以O为圆心，OA长为半径的⊙O与BC 相切于点M，与AB，AD分别相交于点E，F.求证：CD与⊙O相切．5．如图，在Rt△ABC中，∠B＝90°，∠BAC的平分线交BC于点D，E为AB上的一点，DE＝DC，以D为圆心，DB长为半径作⊙D，AB＝5，EB＝3.(1)求证：AC是⊙D的切线；(2)求线段AC的长．参考答案【例1】 证明：法一：连接OD.∵AB ＝AC ，∴∠B ＝∠C.∵OB ＝OD ，∴∠BDO ＝∠B.∴∠BDO ＝∠C.∴OD ∥AC.∵DM ⊥AC ，∴DM ⊥OD.∴DM 与⊙O 相切．法二：连接OD ，AD. ∵AB 是⊙O 的直径，∴AD ⊥BC.∵AB ＝AC ，∴∠BAD ＝∠CAD.∵DM ⊥AC ，∴∠CAD ＋∠ADM ＝90°.∵OA ＝OD ，∴∠BAD ＝∠ODA.∴∠ODA ＋∠ADM ＝90°.即OD ⊥DM ，∴DM 是⊙O 的切线．1.(1)连接OB ，∵OA ＝OB ，∴∠OAC ＝∠OBC.∵OA ⊥OD ，∴∠AOC ＝90°.∴∠OAC ＋∠OCA ＝90°.∵DC ＝DB ，∴∠DCB ＝∠DBC.∵∠DCB ＝∠ACO ，∴∠ACO ＝∠DBC.∴∠DBC ＋∠OBC ＝90°.∴∠OBD ＝90°.∵点B 是半径OB 的外端，∴BD 与⊙O 相切．(2)设BD ＝x ，则CD ＝x ，OD ＝x ＋1，OB ＝OA ＝3，由勾股定理得：32＋x 2＝(x ＋1)2.解得x ＝4.∴BD ＝4.2.(1)连接BD ，则∠DBE ＝90°.∵四边形BCOE 是平行四边形，∴BC ∥OE ，BC ＝OE ＝1.在Rt △ABD 中，C 为AD 的中点，∴BC ＝12AD ＝1.∴AD ＝2.(2)BC 是⊙O 的切线，理由如下：连接OB ，由(1)得BC ∥OD ，且BC ＝OD.∴四边形BCDO 是平行四边形．又∵AD 是⊙O 的切线，∴OD ⊥AD.∴四边形BCDO 是矩形．∴OB ⊥BC ，∴BC 是⊙O 的切线．3.(1)连接OA ，OD ，∵D 为BE 的下半圆弧的中点，∴∠FOD＝90°.∵AC＝FC，∴∠CAF＝∠AFC.∵∠AFC＝∠OFD，∴∠CAF＝∠OFD.∵OA＝OD，∴∠ODF＝∠OAF.∵∠FOD＝90°.∴∠OFD＋∠ODF＝90°.∴∠OAF＋∠CAF＝90°，即∠OAC＝90°.∴AC与⊙O相切．(2)∵半径R＝5，EF＝3，∴OF＝OE－EF＝5－3＝2.在Rt△ODF中，DF＝52＋22＝29.【例2】法一：连接DE，作DF⊥AC，垂足为F.∵AB是⊙D的切线，∴DE⊥AB.∵DF⊥AC，∴∠DEB＝∠DFC＝90°.∵AB＝AC，∴∠B＝∠C.∵BD＝CD，∴△BDE≌△CDF.∴DF＝DE.∴F在⊙D上．∴AC是⊙D的切线．法二：连接DE，AD，作DF⊥AC，F是垂足．∵AB与⊙D相切，∴DE⊥AB.∵AB＝AC，BD＝CD，∴∠DAB＝∠DAC.∵DE⊥AB，DF⊥AC，∴DE＝DF.∴F在⊙D上，∴AC与⊙D相切．4.证明：连接OM，过点O作ON⊥CD，垂足为N，∵⊙O与BC相切于M，∴OM⊥BC.∵正方形ABCD中，AC平分∠BCD，又∵ON⊥CD，OM⊥BC，∴OM＝ON.∴N在⊙O上．∴CD与⊙O相切．5.(1)证明：过点D作DF⊥AC于F.∵∠ABC＝90°，∴AB⊥BC.∵AD平分∠BAC，DF⊥AC，∴BD＝DF.∴点F在⊙D上．∴AC是⊙D的切线．(2)在Rt△BDE和Rt△FDC中，∵BD＝DF，DE＝DC，∴Rt△BDE≌Rt△FDC(HL)，∴EB＝FC.∵AB＝AF，∴AB＋EB＝AF＋FC，即AB＋EB＝AC，∴AC＝5＋3＝8.2022年中考数学复习专题---圆中阴影面积计算班级：___________姓名：___________学号：___________1．如图，直线y kx b=+经过点M(1，√3)和点N(1−，3√3)，A、B是此直线与坐标轴的交点．以AB为直径作⊙C，求此圆与y轴围成的阴影部分面积．2．如图，AAAA是⊙OO的直径，CC,DD是圆上两点，且有BD�=CCDD�，连结AADD,AACC，作DDDD⊥AACC的延长线于点DD．(1)求证：DDDD是⊙OO的切线；(2)若AADD=2√3,∠AADDDD=60∘，求阴影部分的面积．（结果保留ππ）3．如图，AAAA是圆OO的直径，AACC⊥AAAA，DD为圆OO上的一点，AACC=DDCC，延长CCDD交AAAA的延长线于点DD.(1)求证：CCDD为圆OO的切线.(2)若OOFF⊥AADD，OOFF=1，30∠=o，求圆中阴影部分的面积.(结果保留ππ)OAF4．如图，⊙OO是等边ΔAAAACC的外接圆，连接AAOO并延长至点PP，且AAAA=AAPP．（1）求证：PPAA是⊙OO的切线；（2）若AAAA=2√3，求图中阴影部分的面积．（结果保留ππ和根号）5．如图，OO为等边△AAAACC的外接圆，DD为直径CCDD延长线上的一点，连接AADD，AADD=AACC．（1）求证：AADD是⊙O的切线；（2）若CCDD=6，求阴影部分的面积．6．如图，AC为圆O的直径，弦AD的延长线与过点C的切线交于点B，E为BC中点，AC= 4√3，BC=4.（1）求证：DE为圆O的切线；（2）求阴影部分面积.7．已知AB是⊙O的直径，点C是圆O上一点，点P为⊙O外一点，且OP∥BC，∠P＝∠BAC．（1）求证：P A为⊙O的切线；（2）如果OP＝AB＝6，求图中阴影部分面积．8．如图，AAAA为⊙OO的直径，弦CCDD⊥AAAA，垂足为DD，CCDD=4√5，连接OOCC,OODD=2DDAA,FF为圆上一点，过点FF作圆的切线交AAAA的延长线于点GG，连接AAFF,AAFF=AAGG．（1）求⊙OO的半径；（2）求证：AAFF=FFGG；（3）求阴影部分的面积．9．如图，△ABC中，∠C=90º，∠ABC=2∠A，点O在AC上，OA=OB,以O为圆心，OC为半径作圆．（1）求证：AB是⊙O的切线；（2）若BC=3，求图中阴影部分的面积．10．如图，在△ABC中，∠CC=60∘，⊙OO是△ABC的外接圆，点P在直径BD的延长线上，且AB=AP．(1)求证：PA是⊙OO的切线；(2)若AB=2√3，求图中阴影部分的面积.(结果保留ππ和根号)11．如图，AB为圆O的直径，射线AD交圆O于点F，点C为劣弧BF的中点，过点C作CE⊥AD，垂足为E，连接AC(1)求证：CE是圆O的切线(2)若∠BAC＝30°，AB＝4，求阴影部分的面积12．如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD于G,OG:OC=3:5,AB=8.(1)求⊙O的半径；(2)点E为圆上一点,∠ECD=15º,将弧CE沿弦CE翻折,交CD于点F,求图中阴影部分的面积.13．如图，已知⊙O是△ABC的外接圆，AC是直径，∠A＝30°，BC＝4，点D是AB的中点，连接DO并延长交⊙O于点P．（1）求劣弧PC的长（结果保留π）；（2）过点P作PF⊥AC于点F，求阴影部分的面积（结果保留π）.14．如图，四边形ABCD内接于圆O，对角线AC是圆O的直径，DB平分∠ADC，AC长10cm．（1）求点O到AB的距离；（2）求阴影部分的面积．15．如图，在矩形ABCD中，AB=8cm，BC=4cm，以点A为圆心，AD为半径作圆与BA 的延长线交于点E，连接CE，求阴影部分的面积．16．如图，∠APB的平分线过点O，以O点为圆心的圆与PA相切于点C，DE为⊙O的直径．（1）求证：PB是⊙O的切线；（2）若∠CPO＝50°，∠E＝25°，求∠POD；（3）若⊙O的半径为2，CE＝2√3，求阴影部分的面积．17．如图，点P在圆O外，PA与圆O相切于A点，OP与圆周相交于C点，点B与点A 关于直线PO对称，已知OA=4，∠POA=60°求：（1）弦AB的长；（2）阴影部分的面积（结果保留π）．18．如图，⊙O是Rt△ABC的外接圆，直径AB＝4，直线EF经过点C，AD⊥EF于点D，∠ACD＝∠B．（1）求证：EF是⊙O的切线；（2）若AD＝1，求BC的长；（3）在（2）的条件下，求图中阴影部分的面积．。
证明圆的切线经典例题
证明圆的切线方法及例题证明圆的切线常用的方法有:、若直线l过O O上某一点A，证明I是O O的切线，只需连0A，证明OA丄l就行了，简称“连半径，证垂直”，难点在于如何证明两线垂直例1 如图，在△ ABC中，AB=AC，以AB为直径的O O交BC于D，交AC于E, B为切点的切线交0D延长线于F.求证：EF与O 0相切.证明：连结OE, AD.•/ AB是O 0的直径，••• AD 丄BC.n 又••• AB=BC ,•••/ 3= / 4.——• BD=DE，/ 1 = / 2.又••• OB=OE , OF=OF ,•••△ BOF ◎△ EOF ( SAS) •••/OBF= / OEF.••• BF与O O相切，• OB 丄BF.•••/ OEF=9O°.• EF与O O相切.说明：此题是通过证明三角形全等证明垂直的例2 如图，AD 是/ BAC 的平分线，P 为BC 延长线上一点，且 PA=PD.求证：PA 与O O 相切.作直径AE ，连结EC. •/ AD 是/ BAC 的平分线， •••/ DAB= / DAC. •/ PA=PD , •••/ 2= / 1+ / DAC.•••/ 2= / B+ / DAB , •••/ 1 = / B.又•••/ B= / E , •••/ 1 = / E•/ AE 是O O 的直径，• AC 丄 EC , / E+ / EAC=90 .•••/ 1 + / EAC=90°.即OA 丄PA. • PA 与O O 相切.延长AD 交O O 于E ,连结OA , OE.•/ AD 是/ BAC 的平分线, • BE=C ® ,• OE 丄 BC. •••/ E+/ BDE=90 0. •/ OA=OE , •••/ E=/ 1. •/ PA=PD , • / PAD= / PDA. 又•••/ PDA= / BDE, •••/ 1 + / PAD=90 0证明一:证明二:即OA丄PA.• PA与O O相切说明：此题是通过证明两角互余，证明垂直的，解题中要注意知识的综合运用例3 如图，AB=AC , AB是O O的直径，O O交BC于D, DM丄AC于M求证：DM与O O相切.证明一：连结OD.•/ AB=AC ,•••/ B= / C.•/ OB=OD ,•••/ 仁/ B.•••/ 仁/C.• OD // AC.•/ DM 丄AC ,• DM 丄OD.• DM与O O相切证明二：连结OD , AD.•/ AB是O O的直径,• AD 丄BC.又••• AB=AC,• / 1= / 2.•/ DM 丄AC ,•/ 2+Z 4=90°•/ OA=OD ,•/ 仁/3., , 0•/ 3+Z 4=90 .即OD丄DM.• DM是O O的切线.证明二是通过证两角互余证明垂直的，解题中注意充分说明：证明一是通过证平行来证明垂直的利用已知及图上已知例4 如图，已知：AB 是O O 的直径，点 C 在O O 上，且/ CAB=30°, BD=OB , D 在AB 的延长 线上•••• OB=BC.•/ OB=BD , • OB=BC=BD. • OC 丄 CD. • DC 是O O 的切线.此题是根据圆周角定理的推论3证明垂直的，此题解法颇多，但这种方法较好例5 如图，AB 是O O 的直径，CD 丄AB ，且OA 2=OD • OP.2•/ OA =OD • OP , OA=OC ,2• OC 2=OD • OP ,•/ CD 丄 AB ,• / OCP=90 . • PC 是O O 的切线.求证: DC 是O O 的切线 证明: 连结OC 、BC.•/ OA=OC ,又••• OC=OB ,说明:求证: PC 是O O 的切线. 证明: 连结OCOC OP OD OC说明: 此题是通过证三角形相似证明垂直的 PD例6 如图，ABCD是正方形，G是BC延长线上一点，AG交BD于E,交CD于F.求证：CE与厶CFG的外接圆相切.分析：此题图上没有画出△ CFG的外接圆，但△ CFG是直角三角形，圆心在斜边FG的中点，为此我们取FG的中点0,连结0C,证明CE丄OC即可得解.证明：取FG中点0,连结0C.T ABCD是正方形，••• BC 丄CD , △ CFG 是Rt△•/ 0是FG的中点，• 0是Rt A CFG的外心.•/ 0C=0G ,•••/ 3= / G,•/ AD // BC,•/ G= / 4.•/ AD=CD , DE=DE ,o/ ADE= / CDE=45 ,•△ ADE ◎△ CDE (SAS)•••/ 4= / 1,Z 1 = / 3.•••/ 2+ / 3=90°,•••/ 1 + / 2=90°.即CE丄0C.• CE与厶CFG的外接圆相切、若直线l与O O没有已知的公共点，又要证明I是O O的切线，只需作OA丄I, A为垂足，证明OA是O O的半径就行了，简称："作垂直；证半径”例7 如图，AB=AC , D为BC中点，O D与AB切于E点.求证：AC与O D相切.证明一：连结DE,作DF丄AC , F是垂足.••• AB是O D的切线，••• DE 丄AB.•/ DF 丄AC ,•••/ DEB= / DFC=90°.•/ AB=AC ,•••/ B= / C.又••• BD=CD ,•••△ BDE ◎△ CDF (AAS )• DF=DE.• F在O D上.• AC是O D的切线证明二：连结DE , AD，作DF丄AC , F是垂足.••• AB与O D相切，• DE 丄AB.•/ AB=AC , BD=CD ,•••/ 仁/2.•/ DE 丄AB , DF 丄AC ,• DE=DF.• F在O D上.• AC与O D相切.的，证明二是利用角平分线的性质证明DF=DE 说明：证明一是通过证明三角形全等证明DF=DE的，这类习题多数与角平分线有关•例8 已知：如图，AC, BD与O O切于A、B,且AC // BD，若/ COD=90°.求证：CD是O O的切线.证明一：连结OA , OB，作OE丄CD , E为垂足.••• AC , BD 与O O 相切，••• AC 丄OA , BD 丄OB.•/ AC // BD ,, , , , 0•••/ 1 + / 2+ / 3+ / 4=180 .•••/ COD=90°,•/ 2+ / 3=90°,/ 1 + / 4=90°. •••/ 4+ / 5=900.•/ 1 = / 5.• Rt△ AOC s Rt△ BDO.•AC OC"OB - OD .•/ OA=OB ,•A C OC"OA - OD.又•••/ CAO= / COD=900,• △ AOC ODC ,•/ 1 = / 2.又••• OA 丄AC , OE 丄CD,• OE=OA.• E点在O O上.• CD是O O的切线.证明二：连结OA , OB，作OE丄CD于E,••• AC , BD 与O O 相切，• AC 丄OA , BD 丄OB.•/ AC // BD ,•/ F=/ BDO.又••• OA=OB ,•△ AOF ◎△ BOD (AAS )• OF=OD.•••/ COD=90 0,• CF=CD，/ 1= / 2.又••• OA 丄AC , OE 丄CD ,••• OE=OA.••• E点在O O上.• CD是O O的切线.证明连结AO并延长，作OE丄CD于E,取CD中点F，连结OF.三：••• AC与O O相切，• AC 丄AO.•/ AC // BD ,• AO 丄BD.••• BD与O O相切于B,• AO的延长线必经过点 B.• AB是O O的直径.•/ AC // BD，OA=OB，CF=DF ,• OF // AC ,•/ 仁/COF.•••/ COD=9O°, CF=DF ,1•OF CD 二CF .2•/ 2=Z COF.•/ 仁/2.•/ OA 丄AC , OE 丄CD,• OE=OA.• E点在O O上.• CD是O O的切线说明：证明一是利用相似三角形证明/ 1 = / 2，证明二是利用等腰三角形三线合一证明/ 1 = 7 2•证明三是利用梯形的性质证明/ 1 = 7 2，这种方法必需先证明A、O、B三点共线.11。
证明圆的切线经典例题
证明圆的切线方法及例题证明圆的切线常用的方法有：一、若直线l过⊙O上某一点A，证明l是⊙O的切线，只需连OA，证明OA⊥l就行了，简称“连半径，证垂直”，难点在于如何证明两线垂直.例1如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于D，交AC于E，B为切点的切线交OD 延长线于F.求证：EF与⊙O相切.证明：连结OE，AD.∵AB是⊙O的直径，∴AD⊥BC.又∵AB=BC，∴∠3=∠4.⌒⌒∴BD=DE，∠1=∠2.又∵OB=OE，OF=OF，∴△BOF≌△EOF（SAS）.∴∠OBF=∠OEF.∵BF与⊙O相切，∴OB⊥BF.∴∠OEF=900.∴EF与⊙O相切.说明：此题是通过证明三角形全等证明垂直的例2 如图，AD是∠BAC的平分线，P为BC延长线上一点，且PA=PD.求证：PA与⊙O相切.证明一：作直径AE，连结EC.∵AD是∠BAC的平分线，∴∠DAB=∠DAC.∵PA=PD，∴∠2=∠1+∠DAC.∵∠2=∠B+∠DAB，∴∠1=∠B.又∵∠B=∠E，∴∠1=∠E∵AE是⊙O的直径，∴AC⊥EC，∠E+∠EAC=900.∴∠1+∠EAC=900.即OA⊥PA.∴PA与⊙O相切.证明二：延长AD交⊙O于E，连结OA，OE.∵AD是∠BAC的平分线，⌒⌒∴BE=CE，∴OE⊥BC.∴∠E+∠BDE=900.∵OA=OE，∴∠E=∠1.∵PA=PD，∴∠PAD=∠PDA.又∵∠PDA=∠BDE,∴∠1+∠PAD=900即OA⊥PA.∴PA与⊙O相切说明：此题是通过证明两角互余，证明垂直的，解题中要注意知识的综合运用.例3 如图，AB=AC ，AB 是⊙O 的直径，⊙O 交BC 于D ，DM ⊥AC 于M求证：DM 与⊙O 相切.证明一：连结OD.∵AB=AC ，∴∠B=∠C.∵OB=OD ， ∴∠1=∠B.∴∠1=∠C.∴OD ∥AC.∵DM ⊥AC ，∴DM ⊥OD. ∴DM 与⊙O 相切证明二：连结OD ，AD.∵AB 是⊙O 的直径，∴AD ⊥BC. 又∵AB=AC,∴∠1=∠2.∵DM ⊥AC ，∴∠2+∠4=900∵OA=OD ，∴∠1=∠3.∴∠3+∠4=900.即OD ⊥DM. ∴DM 是⊙O 的切线 说明：证明一是通过证平行来证明垂直的.证明二是通过证两角互余证明垂直的，解题中注意充分利用已知及图上已知.D C例4 如图，已知：AB 是⊙O 的直径，点C 在⊙O 上，且∠CAB=300，BD=OB ，D 在AB 的延长线上. 求证：DC 是⊙O 的切线证明：连结OC 、BC.∵OA=OC ，∴∠A=∠1=∠300.∴∠BOC=∠A+∠1=600.又∵OC=OB ，∴△OBC 是等边三角形.∴OB=BC.∵OB=BD ，∴OB=BC=BD.∴OC ⊥CD. ∴DC 是⊙O 的切线. 说明：此题是根据圆周角定理的推论3证明垂直的，此题解法颇多，但这种方法较好. 例5 如图，AB 是⊙O 的直径，CD ⊥AB ，且OA 2=OD ·OP.求证：PC 是⊙O 的切线.证明：连结OC∵OA 2=OD ·OP ，OA=OC ，∴OC 2=OD ·OP ，OCOP OD OC . 又∵∠1=∠1，∴△OCP ∽△ODC.∴∠OCP=∠ODC.∵CD ⊥AB ，∴∠OCP=900.∴PC 是⊙O 的切线.说明：此题是通过证三角形相似证明垂直的例6 如图，ABCD 是正方形，G 是BC 延长线上一点，AG 交BD 于E ，交CD 于F.D求证：CE与△CFG的外接圆相切.分析：此题图上没有画出△CFG的外接圆，但△CFG是直角三角形，圆心在斜边FG的中点，为此我们取FG的中点O，连结OC，证明CE⊥OC即可得解.证明：取FG中点O，连结OC.∵ABCD是正方形，∴BC⊥CD，△CFG是Rt△∵O是FG的中点，∴O是Rt△CFG的外心.∵OC=OG，∴∠3=∠G，∵AD∥BC，∴∠G=∠4.∵AD=CD，DE=DE，∠ADE=∠CDE=450，∴△ADE≌△CDE（SAS）∴∠4=∠1，∠1=∠3.∵∠2+∠3=900,∴∠1+∠2=900.即CE⊥OC.∴CE与△CFG的外接圆相切二、若直线l与⊙O没有已知的公共点，又要证明l是⊙O的切线，只需作OA⊥l，A为垂足，证明OA是⊙O的半径就行了，简称：“作垂直；证半径”例7 如图，AB=AC，D为BC中点，⊙D与AB切于E点.求证：AC与⊙D相切.证明一：连结DE，作DF⊥AC，F是垂足.∵AB是⊙D的切线，∴DE⊥AB.∵DF⊥AC，∴∠DEB=∠DFC=900.∵AB=AC，∴∠B=∠C.又∵BD=CD，∴△BDE≌△CDF（AAS）∴DF=DE.∴F在⊙D上.∴AC是⊙D的切线证明二：连结DE，AD，作DF⊥AC，F是垂足.∵AB与⊙D相切，∴DE⊥AB.∵AB=AC，BD=CD，∴∠1=∠2.∵DE⊥AB，DF⊥AC，∴DE=DF.∴F在⊙D上.∴AC与⊙D相切.说明：证明一是通过证明三角形全等证明DF=DE的，证明二是利用角平分线的性质证明DF=DE的，这类习题多数与角平分线有关.例8 已知：如图，AC，BD与⊙O切于A、B，且AC∥BD，若∠COD=900.求证：CD是⊙O的切线.证明一：连结OA，OB，作OE⊥CD，E为垂足.∵AC，BD与⊙O相切，∴AC ⊥OA ，BD ⊥OB. ∵AC ∥BD ，∴∠1+∠2+∠3+∠4=1800.∵∠COD=900，∴∠2+∠3=900，∠1+∠4=900.∵∠4+∠5=900.∴∠1=∠5.∴Rt △AOC ∽Rt △BDO.∴OD OC OB AC =.∵OA=OB ， ∴ODOC OA AC =. 又∵∠CAO=∠COD=900，∴△AOC ∽△ODC ，∴∠1=∠2.又∵OA ⊥AC ，OE ⊥CD,∴OE=OA.∴E 点在⊙O 上. ∴CD 是⊙O 的切线.证明二：连结OA ，OB ，作OE ⊥CD 于E ，延长DO 交CA 延长线于F.∵AC ，BD 与⊙O 相切，∴AC ⊥OA ，BD ⊥OB.∵AC ∥BD ，∴∠F=∠BDO.又∵OA=OB ，∴△AOF ≌△BOD （AAS ）∴OF=OD.∵∠COD=900，∴CF=CD ，∠1=∠2. 又∵OA ⊥AC ，OE ⊥CD ， O∴OE=OA.∴E 点在⊙O 上. ∴CD 是⊙O 的切线.证明三：连结AO 并延长，作OE ⊥CD 于E ，取CD 中点F ，连结OF.∵AC 与⊙O 相切，∴AC ⊥AO.∵AC ∥BD ，∴AO ⊥BD.∵BD 与⊙O 相切于B ，∴AO 的延长线必经过点B.∴AB 是⊙O 的直径.∵AC ∥BD ，OA=OB ，CF=DF ，∴OF ∥AC ，∴∠1=∠COF.∵∠COD=900，CF=DF ，∴CF CD OF ==21.∴∠2=∠COF.∴∠1=∠2.∵OA ⊥AC ，OE ⊥CD ，∴OE=OA.∴E 点在⊙O 上. ∴CD 是⊙O 的切线说明：证明一是利用相似三角形证明∠1=∠2，证明二是利用等腰三角形三线合一证明∠1=∠2.证明三是利用梯形的性质证明∠1=∠2，这种方法必需先证明A 、O 、B 三点共线.。
人教版数学中考专题复习：圆的切线证明题专项训练
人教版数学中考专题复习：圆的切线证明题专项训练1．如图，在Rt△ABC中，∠B＝90°，AD平分∠BAC交BC于点D，点E在AC上，以AE为直径的∠O经过点D．(1)求证：BC是∠O的切线；(2)若∠C＝30°，且CD＝2．如图，在Rt∠ABC中，∠C=90°，AD平分∠BAC交BC于点D，O为AB上一点，经过点A．D的∠O分别交AB，AC于点E，F．(1)求证：BC是∠O的切线；(2)若BE=8，sin B≈513，求∠O的半径；(3)求证：AD2=AB•AF．3．如图，AB 是O 的直径，D 为O 上一点，点E 为BD 的中点，点C 在BA 的延长线上，且CDA B ∠=∠．(1)求证：CD 是O 的切线；(2)若2DE =，30BDE ∠=︒，求OC 的长．4．如图，∠O 的弦AB 、CD 交于点E ，点A 是CD 的中点，连接AC 、BC ，延长DC 到点P ，连接PB ．(1)若PB ＝PE ，判断PB 与∠O 的位置关系，并说明理由．(2)若AC 2＝2AE 2，求证：点E 是AB 的中点．5．如图，在Rt ABC 中，∠BAC =90°，以AD 为直径的∠O 与边BC 有公共点E ，且AB =BE ．(1)求证：BC是∠O的切线；(2)若BE=3，BC=7，求∠O的半径．⊥于点C，交O于点E，CD与BA的延长线交于点6．如图，AB为O直径，D为O上一点，BC CDF，BD平分ABC∠．(1)求证：CD是O的切线；BC=，求BD的长．(2)若3AB=，27．如图，四边形ABCD内接于∠O，AB是∠O的直径，点P为CA的延长线上一点，∠CAD＝45°．(1)若AB＝8，求图中阴影部分的面积；(2)若BC＝AD，AD＝AP，求证：PD是∠O的切线．8．如图，在∠ABC中，AB＝AC，点D在BC上，BD＝DC，过点D作DE∠AC，垂足为E，∠O经过A，B，D三点．(1)证明：AB是∠O的直径(2)试判断DE与∠O的位置关系，并说明理由；(3)若DE的长为3，∠BAC＝60°，求∠O的半径．9．如图，在Rt∠ABC中，∠ACB＝90°，E是BC的中点，以AC为直径的∠O与AB边交于点D，连接DE．(1)求证：DE是∠O的切线；(2)若CD＝3cm，5cm2DE ，求∠O直径的长．10．如图，点D在∠O的直径AB的延长线上，点C在∠O上，且AC＝CD，∠ACD＝120°．(1)求证：CD是∠O的切线；(2)若∠O的半径为2，求图中阴影部分的面积．11．如图，在∠ABC中，AB=AC，以AB为直径的∠O与BC相交于点D，DE∠AC于E．(1)求证：DE是∠O的切线；(2)若∠O的半径为5，BC=16，求DE的长．12．如图，AB是∠O的直径，C、D是∠O上的点，BD平分∠ABC，DE∠BE，DE交BC的延长线于点E．(1)求证：DE是∠O的切线；(2)如果CE＝1，AC＝∠O的半径r．13．如图，AB是O的直径，点C、G为圆上的两点，当点C是弧BG的中点时，CD垂直直线AG，垂足为D ，直线DC 与AB 的延长线相交于点P ，弦CE 平分ACB ∠，交AB 于点F ，连接BE ．(1)求证：DC 与O 相切；(2)求证：PC PF =；(3)若1tan 3E =，BE =PF 的长．14．如图，∠O 是四边形ABCD 的外接圆，AC 是∠O 的直径，BE ∠DC ，交DC 的延长线于点E ，CB 平分∠ACE ．(1)求证：BE 是∠O 的切线．(2)若AC ＝4，CE ＝1，求tan∠BAD ．15．如图，AB 为∠O 的直径，射线AD 交∠O 于点F ，C 为BF 的中点，过点C 作CE ∠AD ，连接AC ．(1)求证：CE是∠O的切线；(2)若∠BAC＝30°，AB＝4，求阴影部分的面积．16．如图，∠O是△ABC的外接圆，且AB＝AC，四边形ABCD是平行四边形，边CD与∠O交于点E，连接AE．(1)求证△ABC∠∠ADE；(2)求证：AD是∠O的切线．．以AB为直径的O交BC于点D，过点D作DE∠AC于点17．已知：如图，在∠ABC中，AB ACE．(1)求证：DE与O相切；AB ，sin B，求线段AF的长．(2)延长DE交BA的延长线于点F，若618．如图，Rt∠ABC中，∠ABC＝90°，点E为BC的中点，连接DE．(1)求证：DE是半圆∠O的切线；(2)若∠BAC＝30°，DE＝2，求AD的长．19．如图，AB是∠O的直径，点E是劣弧AD上一点，∠PBD＝∠BED，且DEBE平分∠ABD，BE与AD交于点F．(1)求证：BP是∠O的切线；(2)若tan∠DBE EF的长；(3)延长DE，BA交于点C，若CA＝AO，求∠O的半径．20．如图，在Rt△OAB中，∠AOB＝90°，OA＝OB＝4，以点O为圆心、2为半径画圆，过点A作∠O的切线，切点为P，连接OP．将OP绕点O按逆时针方向旋转到OH时，连接AH，BH．设旋转角为α（0°＜α＜360°）．(1)当α＝90°时，求证：BH是∠O的切线；(2)当BH与∠O相切时，求旋转角α和点H运动路径的长；(3)当△AHB面积最小时，请直接写出此时点H到AB的距离．参考答案：1．(1)连接OD，∠AD是∠BAC的平分线，∠∠DAB＝∠DAO，∠OD＝OA，∠∠DAO＝∠ODA，则∠DAB＝∠ODA，∠DO∠AB，而∠B＝90°，∠∠ODB＝90°，∠BC是∠O的切线；(2)连接DE、OD、DF、OF，设圆的半径为R，∠∠C＝30°，CD＝∠OD＝CD•tan30°＝3，∠∠DAB＝∠DAE＝30°，∠DE＝DF，∠∠DOE＝60°，∠∠DOF＝60°，∠∠FOA＝60°，∠∠OFD、△OF A是等边三角形，∠DF∠AC，∠S阴影＝S扇形DFO＝2603360π⨯⨯＝32π．2．(1)证明： 如图，连接OD ，∠OA =OD ，∠∠ODA =∠OAD ，∠AD 平分∠BAC ，∠∠OAD =∠CAD ，∠∠ODA =∠CAD∠OD AC ∥，∠∠C =90°，∠ ∠ODB =∠C =90°，又∠OD 是∠O 的半径，∠BC 是∠O 的切线；(2)解：90BDO ∠=︒，∴在Rt∠BDO 中，5sin 813OD OD OD B BO BE OD OD ====++， 解得5OD =，故∠O 的半径为5；(3)证明：如图：连接EF ，∠AE 是直径，∠90AFE ACB ∠=︒=∠，∠EF BC ∥，∠AEF B ∠=∠，又∠AEF ADF ∠=∠，∠B ADF ∠=∠，又∠OAD CAD ∠=∠，∠∠DAB ∠∠F AD ， ∠AD AF AB AD=， ∠2AD AB AF =⋅．3．(1)解：连接OD ，∠OD OB =，∠B ODB ∠=∠，又∠B CDA ∠=∠，∠ODB CDA ∠=∠，∠AB 是圆O 的直径，∠∠ADB =90°，∠90ODB ODA ∠+∠=︒，∠90CDA ODA ∠+∠=︒即90ODC ∠=︒， ∠CD 是O 的切线；(2)解：连接BE 、OE∠E 是BD 的中点，∠2BE DE ==，OE BD ⊥，260BOE BDE ∠=∠=︒， ∠OBE △是等边三角形，∠2OB BE ==，60BOE ∠=︒∠OB OD =，OE BD ⊥，∠60BOE DOE ∠=∠=︒，∠60DOC ∠=︒在Rt ODC ，60DOC ∠=︒，∠∠C =30°，∠24OC OD ==．4．(1)PB 与∠O 相切，理由是：连接OA 、OB ，OA 交CD 于F ，∠点A 是CD 的中点，∠OA ∠CD ，∠∠AFE ＝90°，∠∠OAE ＋∠AED ＝90°，∠OA＝OB，PB＝PE，∠∠OAE＝∠OBA，∠PEB＝∠PBE，∠∠AED＝∠PEB，∠∠OBA＋∠PBE＝90°，即∠OBP＝90°，∠OB∠PB，∠PB与∠O相切；(2)∠AC＝AD，∠∠ACE＝∠ABC，∠∠CAE＝∠BAC，∠∠ACE∠∠ABC，∠ACAE＝ABAC，∠AC2＝AE•AB，∠AC2＝2AE2，∠AE•AB＝2AE2，∠AB＝2AE，∠E为AB的中点．5．(1)证明：连接OB，OE，如图所示，在ABO和EBO△中，AB BE OA OE OB OB =⎧⎪=⎨⎪=⎩，∠()SSS ABO EBO △△≌， ∠90BEO BAO ∠=∠=︒，即OE BC ⊥,∠BC 是O 的切线；(2)解：∠3BE =，7BC =，∠3AB BE ==，4CE =，∠AC == ∠OE BC ⊥，∠222OE EC OC +=，即()2224OE OE +=，解得：OE = ∠O6．(1)连接OD ，如图，∠BD 平分ABC ∠，∠ABD DBC ∠=∠，∠OB OD =，∠OBD ODB ∠=∠∠DBC ODB ∠=∠，∠∥OD BC ，∠ODF C ∠=∠∠BC CD ⊥，∠90C ∠=︒，∠90ODF C ∠=∠=︒，即OD DC ⊥，∠CD 是O 的切线(2)连接AD ，如图，∠AB 为O 直径，∠90ADB ∠=︒∠90C ∠=︒，∠90ADB C ∠=∠=︒∠ABD DBC ∠=∠，∠ABD DBC △△∽ ∠BC BD BD AB =，即23BD BD =， ∠BD =∠BD ．7．(1)解：如图，连接OC ，OD ，∠∠COD＝2∠CAD，∠CAD＝45°，∠∠COD＝90°，∠AB＝8，∠OC＝12AB＝4，∠S扇形COD＝2904360π⨯⨯＝4π，S△OCD＝12×OC×OD＝12×4×4＝8，∠S阴影= S扇形COD- S△OCD =4π﹣8．(2)证明：∠BC＝AD，∠BC AD=，∠∠BOC＝∠AOD，∠∠COD＝90°，∠∠AOD＝45°，∠OA＝OD，∠∠ODA＝∠OAD，∠∠AOD+∠ODA+∠OAD＝180°，∠∠ODA＝67.5°，∠AD＝AP，∠∠ADP＝∠APD，∠∠CAD＝∠ADP+∠APD，∠CAD＝45°，∠∠ADP＝12∠CAD＝22.5°，∠∠ODP＝∠ODA+∠ADP＝90°，∠PD是∠O的切线．8．(1)解：如图所示，连接AD∠AB＝AC，BD＝DC，∠AD∠BC即∠ADB＝90°，∠AB是∠O的直径．(2)解：DE与∠O相切，理由如下：如图所示，连接OD，∠OB＝OA，BD＝DC，∠OD是∠ABC的中位线，∥．∠OD AC∠DE∠AC，∠DE∠OD即∠ODE＝90°，∠DE与∠O相切．(3)解：∠AB＝AC，AD∠BC，∠BAC＝60°，∠∠BAD＝∠DAE＝30°．∠DE∠AC，AD∠BD，∠AD＝2DE＝6，AB＝2BD．在∠ABD 中，222BD AD AB +=， ∠()22262BD BD +=，解得BD =∠2AB BD ==，∠∠O 的半径为9．(1)连接OD∠AC 为圆O 的直径 ∠∠ADC ＝90°∠OD ＝OC∠∠ODC ＝∠OCD在Rt ∠BCD 中，∠E 为BC 中点 ∠12DE BC CE == ∠∠EDC ＝∠ECD∠∠ODC ＋∠EDC ＝∠OCD ＋ECD ＝90° 即∠ODE ＝90°∠OD ∠DE∠DE 是圆O 的切线(2)在Rt∠BCD中，∠E为BC中点∠BC＝2DE＝5∠CD＝3∠BD=4∠AC为直径，∠∠ADC＝∠ACB＝∠BDC＝90°，又∠∠B＝∠B∠∠ABC∠∠CBD，∠AC BC CD BD=∠5 34 AC=∠154=AC cm10．(1)证明：如图，连接OC，∠CD＝AC，∠∠CAD＝∠D，又∠∠ACD＝120°，∠∠CAD＝∠D＝12（180°﹣∠ACD）＝30°，∠OC＝OA，∠∠A＝∠2＝30°，∠∠COD＝60°，又∠∠D＝30°，∠∠OCD＝180°﹣∠COD﹣∠D＝90°，∠OC∠CD∠OC是∠ O的半径∠CD是∠ O的切线；(2)解：∠∠A ＝30°，∠∠1＝2∠A ＝60°． ∠260223603OBC S ππ⨯==扇形 ，在Rt ∠OCD 中，tan 60CD OC ==•︒=∠11222Rt OCD S OC CD =⨯=⨯⨯=△．∠图中阴影部分的面积为23π．11．(1)证明：如图：连接OD ．∠AB =AC ，∠∠B =∠C ，又∠OD =OB ，∠∠ODB =∠OBD ．∠∠ODB =∠ACB ．∠OD AC ∥，∠DE ∠AC ．∠OD ∠DE ．∠OD 是圆的半径，∠DE 是∠O 的切线；(2)解：如图：连接AD ，∠AB为∠O的直径，∠∠ADB=90°，即AD∠BC，又∠AB=AC，BC=16，∠BD=CD=8，∠∠O的半径为5，∠AC=AB=10，∠6 AD=，∠S△ADC11••22AC DE CD AD ＝＝，∠10DE=8×6，∠DE=4.8．12．(1)解：连接OD，如下图所示：∠OB=OD，∠∠OBD=∠ODB，∠BD平分∠ABC，∠∠OBD=∠DBE，∠∠ODB=∠DBE，∠OD∥BE，∠DE∠BE于点E，∠∠E=90°，∠∠ODE=180°-∠E=180°-90°=90°，∠OD∠DE；∠DE是∠O的切线．(2)解：设OD交AC于点M，如下图：∠AB为∠O的直径，∠∠ACB=∠ACE=90°，由(1)知，∠ODE=90°，∠∠ACE=∠E=∠ODE=90°，∠四边形DECM为矩形，∠EC=DM=1，∠MO∥CB，O为AC的中点，∠MO为∠ABC的中位线，且∠AMO=∠ACB=90°，AC∠AM=MC=12设圆的半径为r，则MO=DO-DM=r-1，在Rt∠AMO中，由勾股定理可知：AO²=AM²+MO²，代入数据：222=+-，r r(1)解出：4r=，故圆∠O的半径为4．13．(1)解：（1）CD AD ⊥，90D ∴∠=︒，∠∠DAC +∠DCA =90°，点c 是弧BG 的中点，∠CG BC =DAC BAC ∴∠=∠，OA OC =，OCA BAC ∴∠=∠，OCA DAC ∠=∠∴，//∴AD OC ，∠∠D =∠OCP =90°， OC 是圆O 的半径，DC ∴与O 相切，(2) AB 是O 的直径，90ACB ∴∠=︒，90PCB ACD ∴∠+∠=︒，由（1）得：90DAC DCA ∠+∠=︒，PCB DAC ∴∠=∠，DAC BAC ∠=∠，PCB BAC ∴∠=∠， CE 平分ACB ∠，ACF BCF ∴∠=∠，∠∠PFC =∠BAC +∠ACF ，∠PCF =∠PCB +∠BCF ，PFC PCF ∴∠=∠，PC PF ∴=；(3)连接AE ，CE 平分ACB ∠，∴AE BE =，AE BE ∴=， AB 是O 的直径，90AEB ∴∠=︒，AEB ∴∆为等腰直角三角形，∠AB ，∠OB =OC ∠1tan 3E = ∠1tan 3BC CAB AC ==∠， ∠∠PCB =∠BAC ，∠P =∠P ，∠△PCB ∠△P AC ， ∠13BC PB AC PC ==， ∴设PB x =，3=PC x ，在Rt OCP ∆中，222OC PC OP +=，∠222(3))x x +=，∠x =x =0(舍去)，∠PC∠PF 14．(1)证明：如图，连接OB，∠CB平分∠ACE．∠∠ACB＝∠ECB，∠OB＝OC，∠∠BCO＝∠CBO，∠∠BCE＝∠CBO，∠OB∠ED．∠BE∠ED，∠EB∠BO．∠BE是∠O的切线；(2)解：∠AC是∠O的直径，∠∠ABC＝90°，∠BE∠ED，∠∠E＝90°，∠∠E＝∠ABC，∠∠BCE＝∠ACB，∠∠BCE∠∠ACB，∠BC CE AC BC=，∠AC＝4，CE＝1，∠2BC==，∠BE，∠∠BCD+∠BAD＝∠BCD+∠BCE＝180°，∠∠BCE＝∠BAD，∠tan tan BE BAD BCE CE∠=∠== 15．(1) 解：（1）连接BF ，OC ，∠AB 是∠O 的直径，∠∠AFB ＝90°，即BF ∠AD ，∠CE ∠AD ，∠BF ∠CE ，∠点C 为劣弧BF 的中点，∠OC ∠BF ，又BF ∠CE ，∠OC ∠CE ，∠OC 是∠O 的半径，∠CE 是∠O 的切线；(2)解：连接OF ，CF ，∠OA ＝OC ，∴∠OCA =∠BAC ＝30°，∠∠BOC ＝60°，∠点C 为劣弧BF 的中点，∠FC BC =，∠∠FOC ＝∠BOC ＝60°，∠OF ＝OC ，∴△FOC为等边三角形，∠∠OCF＝∠COB=60°，∠CF∠AB，∠S△ACF＝S△OCF，∠阴影部分的面积等于S扇形COF，∠AB＝4，∠FO＝OC＝OB＝2，∠S扇形FOC＝260223603ππ⋅⨯=，即阴影部分的面积为23π．16．(1)解：∠四边形ABCD是平行四边形，∠∠B＝∠D．∠四边形ABCE为∠O的内接四边形，∠∠B+∠AEC＝180°．∠∠AED+∠AEC＝180°．∠∠B＝∠AED．∠AB＝AC，∠AB＝∠ACB∠∠ACB＝∠AED．∠∠ABC∠∠ADE．(2)解：如图，连接AO并延长，交BC于点M，连接OB、OC．∠AB＝AC，OB＝OC，∠AM垂直平分BC．∠∠AMC＝90°．∠四边形ABCD是平行四边形，∠AD∠BC．∠∠DAO＝90°．∠点A在∠O上，∠AD是∠O的切线．17．(1)证明：连接OD，∠AB=AC，∠=∠，∠B C=，又∠OB OD∠1∠=∠，B∠C1∠=∠，∥，∠OD AC∠DE∠AC于E，∠DE∠OD，∠OD是O的半径，∠DE与O相切；(2)解：如图：连接AD，∠AB为O的直径，∠∠ADB=90°，∠AB =6，sin B∠sin AD AB B =⋅ ∠123290∠+∠=∠+∠=︒， ∠13∠=∠，∠3B ∠=∠，在∠AED 中，∠AED =90°，∠sin 3AE AD ∠==∠65AE AD ===. 又∠OD AE ∥， ∠∠FAE ∠∠FOD ， ∠FA AE FO OD=， ∠6AB =，∠3OD AO ==， ∠235FA FA =+， ∠2AF =．18．(1)连接OD ，BD ，如图，AB 是直径，90ADB ∴∠=︒， 90BDC ∴∠=︒，E 是BC 的中点，12DE BE EC BC ∴=== EBD EDB ∠∠∴=，OB OD =OBD ODB ∠∠∴=OBD EBD ODB EDB ∠∠∠∠∴+=+即90ODE ABC ∠=∠=︒OD DE ∴⊥ OD 是半径，∴DE 是半圆∠O 的切线．(2)2DE =24BC ED ∴==30BAC ∠=︒28AC BC ∴==AB ∴==12BD AB ∴==6AD ∴=．19．(1) 证明：∠AB 是∠O 的直径，∠∠ADB ＝90︒，∠∠DAB +∠ABD ＝90︒，∠∠BED ＝∠DAB ，∠PBD ＝∠BED ，∠∠DAB ＝∠PBD ，∠∠PBD +∠ABD ＝90︒，∠∠ABP ＝90︒，∠AB ∠PB ，∠BP 是∠O 的切线；(2)解：连接AE ，∠AB 是直径∠∠AEB ＝90︒，∠BE 平分∠ABD ，∠∠ABE ＝∠DBE ，∠AE DE =，∠AE ＝DE∠∠ABE ＝∠DBE ＝∠DAE ，∠tan tan tan EF DBE ABE DAE EA ∠∠∠==＝＝，∠EF (3)解：连接OE ，∠OE =OB ，∠∠ABE =∠OEB ，∠∠ABE =∠DBE ，∠∠DBE =∠OEB ，∠//OE BD ∠CE OC DE OB=， ∠CA =AO ，设CA =AO =BO =R ， ∠22CE R DE R==，2=， ∠CE∠DC = CE +DE∠∠ADC =∠ABE ，∠C =∠C ，∠CAD CEB △∽△， ∠CD AC CB CE=，= ∠R，∠∠O20．(1)证明：∠α＝90°，∠AOB ＝90°，∠∠AOP ＝∠BOH ，在∠AOP 和∠BOH 中，OA OB AOP BOH OP OH =⎧⎪∠=∠⎨⎪=⎩∠∠AOP ∠∠BOH （SAS ），∠∠OP A＝∠OHB，∠AP是∠O的切线，∠∠OP A＝90°，∠OHB＝90°，即OH∠BH于点H，∠BH是∠O的切线；(2)如图，过点B作∠O的切线BC，BD，切点分别为C，D，连接OC，OD，则有OC∠BC，OD∠BD，∠OC＝2，OB＝4，∠cos2142OCBOCOB===∠∠∠BOC＝60°，同理∠BOD＝60°，当点H与点C重合时，由（1）知：α＝90°，∠∠OHB＝90°．∠圆弧PH的长为902180ππ⨯=；当点H与点D重合时，α＝∠POC+∠BOC+∠BOD＝90°+2×60°＝210°，∠圆弧PH的长为21027 1803ππ⨯=，∠当BH与∠O相切时，旋转角α＝90°或210°，点H运动路径的长为π或73π；(3)设h表示点H到直线AB的距离，作ON∠AB于点N，H在圆O上，在Rt∠ONB中，∠OBN＝45°，OB＝4，∠ON＝4cos45°＝∠h的最小值为＝ON﹣r＝2∠当∠AHB面积最小时，点H到AB的距离为2。
圆的切线证明方法专题(基础篇)(专项练习)
专题2.10 圆的切线证明方法专题（基础篇）（专项练习） 1．如图，AD 是⊙O 的弦，AB 经过圆心O 交⊙O 于点C ，∠A ＝∠B ＝30°，连接BD ．求证：BD 是⊙O 的切线．2．如图，AB 是⊙O 的直径，点C 在⊙O 上，过点C 的直线与AB 延长线相交于点P ．若∠COB ＝2∠PCB ，求证：PC 是⊙O 的切线．3．如图，AD ，BD 是O 的弦，AD BD ⊥，且28BD AD ==，点C 是BD 的延长线上的一点，2CD =，求证：AC 是O 的切线．4．如图，点P 是O 的直径AB 延长线上的一点（PB OB <），点E 是线段OP 的中点．在直径AB 上方的圆上作一点C ，使得EC EP =．求证：PC 是O 的切线．5．如图，在△ABC 中，∠A=45°，以AB 为直径的⊙O 交于AC 的中点D ，连接CO ，CO 的延长线交⊙O 于点E ，过点E 作EF ⊥AB ，垂足为点G ．（1）求证：BC 时⊙O 的切线；（2）若AB=2，求线段EF 的长．6．如图，AB 是O 的直径，CD 是O 的切线，切点为C ，BE CD ⊥，垂足为E ，连接,AC BC .（1）求证：BC 平分ABE ∠；（2）若60A ∠=︒，2OA =，求CE 的长.7．如图，AB是⊙O的直径，弦CD⊥AB于点E，AM是△ACD外角∠DAF的平分线.(1)求证：AM是⊙O的切线.(2)若C是优弧ABD的中点，AD＝4，射线CO与AM交于N点，求ON的长.8．如图，在△ABC中，AB＝AC，O是边AC上的点，以OC为半径的圆分别交边BC、AC 于点D、E，过点D作DF⊥AB于点F．（1）求证：直线DF是⊙O的切线；（2）若OC＝1，∠A＝45°，求劣弧DE的长．9．如图，已知△ABC内接于⊙O，点D在OC的延长线上，CD＝CB，∠D＝∠A（1）求证：BD是⊙O的切线；（2）若BC＝2，求BD的长．10．已知：如图，AB是O的直径，点C在O上，BD平分 ABC，AD＝AE，AC与BD 相交于点E．(1) 求证：AD是O的切线．(2) 若AD＝DE＝2，求BC的长．11．如图，已知AB是⊙O的直径，BD是⊙O的弦，延长BD到C，使DC=BD，连接AC，过点D作DE⊥AC，垂足为E．（1）求证：AB=AC；（2）求证：DE是⊙O的切线；（3）若⊙O的半径为6，∠BAC=60°，则DE=________．12．已知AB是⊙O的直径，点C在AB的延长线上，AB＝4，BC＝2，P是⊙O上半部分的一个动点，连接OP，CP．(1) 如图①，△OPC的最大面积是________；(2) 如图②，延长PO交⊙O于点D，连接DB，当CP＝DB时，求证：CP是⊙O的切线．13．如图，在Rt ABC △中，90ACB ∠=︒，延长CA 到点D ，以AD 为直径作O ，交BA 的延长线于点E ，延长BC 到点F ，使BF EF =．(1) 求证：EF 是O 的切线；(2) 若9OC =，4AC =，8AE =，求BE 的长．14．如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，且DC ＝AD ．过点A 作⊙O 的切线，过点C 作DA 的平行线，两直线交于点F ，FC 的延长线交AB 的延长线于点G ．(1) 求证：FG 与⊙O 相切；(2) 连接EF ，若AF ＝2，求EF 的长．15．如图，Rt △ABC ，∠ABC =90°，点O 在AB 上，AD ⊥CO 交CO 延长线于点D ，∠DAO =∠ACO ，以点O 为圆心，OB 为半径作圆．(1) 求证：AC 是⊙O 的切线；(2) 已知68CB AB ==，，求OC 的长？16．如图所示，AB 为⊙O 的直径，在△ABC 中，AB =BC ，AC 交⊙O 于点D ，过点D 作DE ⊥BC ，垂足为点E ．(1) 证明DE 是⊙O 的切线；(2) AD =8，P 为⊙O 上一点，P 到弦AD 的最大距离为8．① 尺规作图作出此时的P 点，保留作图痕迹；② 求DE 的长．17．如图，线段AB 经过O 的圆心O ，交圆O 于点A ，C ，1BC =，AD 为O 的弦，连接BD ，30BAD ABD ∠=∠=︒，连接DO 并延长交O 于点E ，连接BE 交O 于点M ．(1) 求证：直线BD 是O 的切线；(2) 求线段BM 的长．18．如图，Rt ABC △中，90C ∠=︒，点O 在AC 上，以OA 为半径的半圆O 分别交AB ，AC 于点D ，E ，过点D 作半圆O 的切线DF ，交BC 于点F ．(1) 求证：BF DF =；(2) 若4AO CE ==，1CF =，求BF 的长．19．如图，在Rt △AOB 中，∠AOB ＝90°，⊙O 与AB 相交于点C ，与AO 相交于点E ，连接CE ，已知∠AOC ＝2∠ACE ．(1) 求证：AB 为⊙O 的切线；(2) 若AO ＝20，BO ＝15，求AE 的长．20．如图，ABC 内接于O ，AC 是O 的直径，点D 是O 上一点，连接CD 、AD ，过点B 作BE AD ⊥，交DA 的延长线于点E ，AB 平分CAE ∠．(1) 求证：BE 是O 的切线；(2) 若30ACB ∠=︒，O 的半径为6，求BE 的长．21．如图，在Rt △ABC 中，∠ABC ＝90°，∠BAC 的平分线交BC 于点O ，D 为AB 上的一点，OD ＝OC ，以O 为圆心，OB 的长为半径作⊙O ．(1) 求证：AC 是⊙O 的切线；(2) 若AB ＝6，BD ＝2，求线段AC 的长．22．如图，在△ABC中，AB=AC，以AB为直径的⊙O与BC相交于点D，过点D作DE⊥AC交AC于点E．(1) 试判断直线DE与⊙O的位置关系，并说明理由；(2) 若⊙O的半径为5，BC=16，求DE的长．∠=︒，以AC为直径作O，交AB于点D，E为BC的23．如图，在Rt ABC中，ACB中点，连接DE并延长交AC的延长线于点E．(1)求证：DF是O的切线；(2)若2CF=，4DF=，求O的半径．24．如图，AB为⊙O的直径，点C在⊙O上，点P在BA的延长线上，连接BC，OC，PC．若AB＝6，AC的长为π．(1) 求∠AOC的度数；(2) 若BC＝PC，求证：直线PC与⊙O相切．参考答案1．证明见分析【分析】连接OD，求出∠ODB＝90°，根据切线的判定推出即可．解：如图，连接OD，∵OD＝OA，∴∠ODA＝∠DAB＝30°，∴∠DOB＝∠ODA+∠DAB＝60°，∴∠ODB＝180°﹣∠DOB﹣∠B＝180°﹣60°﹣30°＝90°，即OD⊥BD，∴直线BD与⊙O相切．【点拨】此题主要考查了切线的判定，三角形的内角和以及三角形的外角性质，关键是证明OD⊥BD．2．证明见分析．【分析】利用半径OA＝OC可得∠COB＝2∠A，然后利用∠COB＝2∠PCB即可证得结论，再根据圆周角定理，易得∠PCB＋∠OCB＝90°，即OC⊥CP；故PC是⊙O的切线．解：连接AC，∵OA＝OC，∴∠A＝∠ACO．∴∠COB＝2∠ACO．又∵∠COB＝2∠PCB，∴∠ACO＝∠PCB．∵AB是⊙O的直径，∴∠ACO+∠OCB＝90°．∴∠PCB+∠OCB＝90°，即OC⊥CP．∵OC是⊙O的半径，∴PC是⊙O的切线．【点拨】此题主要考查了圆的切线的判定及圆周角定理的运用，关键是利用半径OA ＝OC 可得∠COB ＝2∠A ．3．证明见分析．【分析】先由勾股定理的逆定理证明垂直，再由切线的判断进行解答即可．证明：连接AB ，∵AD BD ⊥，且28BD AD ==∴AB 为直径，AB 2=82+42=80，∵CD =2，AD =4∴AC 2=22+42=20∵CD =2，BD =8,∴BC 2=102=100∴222AC AB CB +=，∴90BAC ∠=︒∴AC 是O 的切线．【点拨】本题考查切线的判定，圆周角定理的推论，勾股定理的逆定理，解题关键是作出辅助线构造直角三角形．4．证明见分析【分析】连接OC ，根据线段中点的定义得到OE ＝EP ，求得OE ＝EC ＝EP ，得到∠COE ＝∠ECO ，∠ECP ＝∠P ，利用三角形内角和定理求出90ECO ECP ∠+∠=︒，根据切线的判定定理即可得到结论．证明：连接OC ，∵点E 是线段OP 的中点，∴OE EP =，∵EC EP =，∴OE EC EP ==，∴COE ECO ∠=∠，ECP P ∠=∠，∵180COE ECO ECP P ∠+∠+∠+∠=︒，∴90ECO ECP ∠+∠=︒，∴OC PC ⊥，∵OC 是O 的半径，∴PC 是O 的切线．【点拨】本题考查了切线的判定，等边对等角，三角形内角和定理，熟练掌握切线的判定定理是解题的关键．5．（1）证明参见分析；（2 试题分析：（1）连接BD ，由圆周角性质定理和等腰三角形的性质以及已知条件证明∠ABC=90°即可；（2）根据AB=2，则圆的直径为2，所以半径为1，即OB=OE=1，利用勾股定理求出CO 的长，再通过证明△EGO ∽△CBO 得到关于EG 的比例式可求出EG 的长，进而求出EF 的长．解：（1）如图：连接BD ，∵AB 为⊙O 的直径，∴∠ADB=90°，∴BD ⊥AC ，∵AD=CD ，∴AB=BC ，∴∠A=∠ACB=45°，∴∠ABC=90°，∴BC 是⊙O 的切线；（2）∵AB=2，∴BO=1，∵AB=BC=2，∴EF ⊥AB ，BC ⊥AB ，∴EF ∥BC ，∴△EGO ∽△CBO ，∴EG EOBC CO =，∴2EG =，∴考点：1.切线的判定；2.相似三角形的判定与性质；3.勾股定理的运用.6．（1）详见分析；（2）CE 【分析】（1）利用切线的性质得OC ⊥DE ，再证明OC ∥BE 得到∠OCB ＝∠CBE ，加上∠OCB ＝∠CBO ，所以∠OBC ＝∠CBE ；（2）利用圆周角定理得到∠ACB ＝90°，再证明△OAC 等边三角形得到AC ＝OA ＝2，再利用勾股定理可计算出BC ＝Rt △CBE 中利用含30度的直角三角形三边的关系求CE 的长．（1）证明：∵CD 是O 的切线，∴OC DE ⊥，又∵BE DE ⊥，∴OC BE ，∴OCB CBE ∠=∠，∴OBC CBE ∠=∠，即BC 平分ABE ∠；（2）解：∵AB 为O 的直径，∴90ACB ∠=︒，∵60A ∠=︒，∴OAC 是等边三角形，2AC OA ==.∴24AB OA ==，∴BC =∵1302OBC AOC ∠=∠=︒，且OBC CBE ∠=∠， ∴30CBE ∠=︒.∴12CE BC ==【点拨】本题考查了切线的性质：经过半径的外端且垂直于这条半径的直线是圆的切线；常常“遇到切点连圆心得半径”．7．(1)证明见分析；(2)ON . 【分析】(1)根据垂径定理得到AB 垂直平分CD ，根据线段垂直平分线的性质得到AC ＝AD ，得到∠BAD ＝12∠CAD ，由AM 是△ACD 的外角∠DAF 的平分线，得到∠DAM ＝12∠FAD ，于是得到结论；(2)证明△ACD 是等边三角形，得到CD ＝AD ＝4，根据直角三角形的性质即可得到结论.(1)证明：∵AB 是⊙O 的直径，弦CD ⊥AB 于点E ，∴AB 垂直平分CD ，∴AC ＝AD ，∴∠BAD ＝12∠CAD ，∵AM 是△ACD 的外角∠DAF 的平分线，∴∠DAM ＝12∠FAD ，∴∠BAM ＝12(∠CAD+∠FAD)＝90°，∴AB ⊥AM ，∴AM 是⊙O 的切线；(2)解：∵AC ＝AD ，C 是优弧ABD 的中点，∴AC ＝AD ＝CD ，∴△ACD 是等边三角形，∴CD ＝AD ＝4，60CAD ACD ︒∠=∠=由（1）知AB 垂直平分CD ，则AB 平分CAD ∠∴CE ＝DE ＝2，1302CAE CAD ︒∠=∠= OC OA =30ACO CAE ︒∴∠=∠=30OCE ACD ACO ︒∴∠=∠-∠=在Rt OCE 中，设OC x =，则12OE x = 根据勾股定理得222OE CE OC +=，即2221()22x x +=解得x =∴OC ＝OA ∵∠ANO ＝∠OCE ＝30°，∴ON ＝2OA . 【点拨】本题是圆与三角形的综合题，涉及的知识点主要有切线的判定、垂径定理、等边三角形的判定与性质、直角三角形30度角的性质，灵活利用圆与三角形的相关性质是解题的关键.8．（1）详见分析；（2）34π． 【分析】（1）连结OD ，根据等腰三角形的性质得到OD ∥AB ，根据平行线的性质得到∠ODF ＝90°，根据切线的判定定理证明；（2）根据平行线的性质得到∠AOD ＝180°﹣45°＝135°，根据弧长公式计算即可． 证明：如图，连结OD ，∵AB＝AC，∴∠B＝∠ACB，∵OC＝OD，∴∠ODC＝∠ACB，∴∠B＝∠ODC，∴OD∥AB，∵DF⊥AB，∴∠ODF＝∠BFD＝90°，∵OD为半径，∴直线DF是⊙O的切线；（2）解：∵∠A＝45°，OD∥AB，∴∠AOD＝180°﹣45°＝135°，∴劣弧DE的长为1353 1804ππ⨯=．【点拨】本题主要考查了切线的判定及弧长的计算，熟练掌握切线的判定定理及弧长的计算公式是解题的关键.9．（1）见分析；（2）BD＝【分析】（1）由等腰三角形的性质得出∠CBD+∠OBC＝90°，则∠OBD＝90°，可得出结论；（2）证明△OBC为等边三角形，得出∠BOC＝60°，根据直角三角形的性质可得出答案．（1）证明：∵OB＝OC，∴∠OBC＝∠OCB，∴∠BOC+2∠OBC＝180°，∵∠BOC＝2∠A，∴∠A+∠OBC＝90°，又∵BC＝CD，∴∠D＝∠CBD，∵∠A＝∠D，∴∠CBD+∠OBC＝90°，∴∠OBD＝90°，∴OB⊥BD，∴BD是⊙O的切线；（2）解：∵∠OBD＝90°，∠D＝∠CBD，∴∠OBC＝∠BOC，∴OC＝BC，又∵OB＝OC，∴△OBC为等边三角形，∴∠BOC＝60°，∵BC＝2，∴OB＝2，∴BD＝【点拨】本题考查切线的判定，等腰三角形的性质，圆周角定理，直角三角形的性质，等边三角形的判定与性质，熟练掌握切线的判定是解题的关键．10．(1)见分析【分析】（1）根据AB是O的直径，可得∠C＝90°，由BD平分∠ABC，可得∠CBD＝∠ABD，根据AD＝AE，可得∠CEB＝∠DEA，进而可得∠BAD＝90°，即可得证；（2）连接AF，根据等腰三角形的性质可得DF＝12DE＝1，勾股定理求得AF，证明△AEF≌△BEC，即可求解．（1）∵AB是O的直径，∴∠C＝90°，∴∠CBE＋∠CEB＝90°，∵BD平分∠ABC，∴∠CBD＝∠ABD，∵AD＝AE，∴∠D＝∠AED，∵∠CEB＝∠DEA，∴∠ABD＋∠D＝∠CBE ＋∠CEB＝90°，即∠BAD＝90°，∴AD是⊙O的切线，（2）连接AF，如图，∵AB是O的直径，∴∠AFB＝90°，即AF BD⊥，∵AD＝DE＝2，∴DF＝12DE＝1，在Rt ADF∆中，AD＝2，DF＝1，∴AF＝41-＝3，∵∠DBA＋∠D＝∠EAB＋∠DAE＝90°，∠D＝∠DAE＝60°，∴∠DBA＝∠EAB，∴AE＝BE，又∠AFE＝∠C＝90°，∠AEF＝∠CEB，∴△AEF≌△BEC（AAS），∴BC＝AF【点拨】本题考查了直径所对的圆周角是直角，切线的判定，勾股定理，全等三角形的性质与判定，掌握以上知识是解题的关键．11．（1）见分析；（2）见分析；（3）【分析】（1）连接AD，由直径所对的圆周角度数及中点可证AD是BC的垂直平分线，根据线段垂直平分线的性质可得结论；（2）连接OD，由中位线的性质可得OD∥AC，由平行的性质与切线的判定可证；（3）易知ABC是等边三角形，由等边三角形的性质可得CB长及C∠度数，利用直角三角形30度角的性质及勾股定理可得结果.解：（1）连接AD．∵AB是⊙O的直径，∴∠ADB=90°．∴⊥AD BC又∵DC=BD，∴AD是BC的垂直平分线∴AB=AC．（2）连接OD．∵DE⊥AC，∴∠CED=90°．∵O为AB中点，D为BC中点，∴OD∥AC．∴∠ODE=∠CED=90°．∴DE是⊙O的切线．=（3）由（1）得AC AB60BAC ∠=︒ABC ∴是等边三角形60,2612C BC AB ︒∴∠===⨯=162DC BD BC ∴=== 在Rt CED 中，906030CDE ︒︒︒∠=-=132CE CD ∴== 根据勾股定理得222CE DE CD +=DE ∴【点拨】本题考查了圆与三角形的综合，涉及的知识点主要有圆的切线的判定、圆周角定理的推论、垂直平分线的性质、等边三角形与直角三角形的性质，灵活的将图形与已知条件相结合是解题的关键.12．(1)4(2)见分析【分析】（1）因为OC 长度确定，所以当点P 到OC 的距离最大时△OPC 的面积最大，当OP ⊥OC 时，当点P 到OC 的距离最大，等于圆O 的半径，求出此时的△OPC 的面积即可；（2）连接AP ，BP ，利用同圆中，相等的圆心角所对的弦相等，可得AP =DB ，因为CP ＝DB ，所以AP =CP ，可证△APB ≌△CPO （SAS ），得到∠OPC ＝90°，即可证明CP 是切线．(1)解：∵AB ＝4，∴OB ＝2，OC ＝OB +BC ＝4．在△OPC 中，设OC 边上的高为h ，∵S △OPC 12=OC •h ＝2h ， ∴当h 最大时，S △OPC 取得最大值．作PH ⊥OC ，如图①，则PO PH >，当OP ⊥OC 时，PO PH =，此时h 最大，如答图1所示：此时h ＝半径＝2，14242OPC S ⨯⨯＝＝．∴△OPC 的最大面积为4，故答案为：4．(2)证明：如答图②，连接AP ，BP ．∵∠AOP ＝∠BOD ，∴AP ＝BD ，∵CP ＝DB ，∴AP ＝CP ，∴∠A ＝∠C ，在△APB 与△CPO 中，AP CP A C AB CO =⎧⎪∠=∠⎨⎪=⎩，∴△APB ≌△CPO （SAS ），∴∠APB ＝∠OPC ，∵AB 是直径，∴∠APB ＝90°，∴∠OPC ＝90°，∴DP ⊥PC ，∵DP 经过圆心，∴PC 是⊙O 的切线．【点拨】本题考查了圆，熟练掌握圆的半径、切线、弦与圆心角的关系等知识是解题的关键．13．(1)见分析(2)13【分析】（1）连接OE ，根据等边对等角可得OEA OAE ∠=∠，FEB B ∠=∠，根据对顶角相等，等量代换后可得90OEA FEB ∠+∠=︒即可得证；（2）过点O 作OG BE ⊥，根据垂径定理可得4AG AC ==，由945AO OC AC =-=-=，证明AOG ≌ABC ，可得5AB =，根据BE EA AB =+即可求解．（1）如图，连接OE ，Rt ABC △中，90ACB ∠=︒，90CAB B ∴∠+∠=︒，OE OA =，OEA OAE ∴∠=∠，OAE CAB ∠=∠，90OEA B ∴∠+∠=︒，BF EF =，FEB B ∴∠=∠，90OEA FEB ∴∠+∠=︒，即90FEO ∠=︒，OE 是半径，∴EF 是O 的切线； （2）如图，过点O 作OG BE ⊥，8AE =，124EG AG AE ∴===，9OC =，4AC =，945AO OC AC ∴=-=-=，在AOG 与ABC 中，904OGA BCA AG AC GAO CAB ∠=∠=︒⎧⎪==⎨⎪∠=∠⎩∴AOG ≌ABC ，5AB AO ∴==，5813BE BA AE ∴=+=+=，【点拨】本题考查了切线的判定定理，垂径定理，掌握以上知识是解题的关键． 14．(1)见分析(2)EF =【分析】（1）连接OC ，AC ．先证明△ACD 为等边三角形．可得∠ACO =∠OAC =30°．再由FG ∥DA ，可得∠ACF =∠DAC =60°．从而得到∠OCF =90°．即可求证；（2）根据AD ∥FG ，可得∠AGF =∠DAE =30°．再根据直角三角形的性质可得FG =2AF =4，AG ADE ≌△GCE ．可得AE=GE即可求解．(1)证明：连接OC，AC．∵AB是⊙O的直径，CD⊥AB，∴CE=DE，AD=AC．∵DC=AD，∴DC=AD=AC．∴△ACD为等边三角形．∴∠D=∠DCA=∠DAC=60°．∴∠AOC=30°，∵OA=OC，∴∠ACO=∠OAC=30°．∵FG∥DA，∴∠ACF=∠DAC=60°．∴∠OCF=90°．∴OC⊥FG．∵OC为半径，∴FG与⊙O相切．(2)解：∵AD∥FG，∴∠AGF=∠DAE=30°．∵AF为⊙O的切线，∴∠F AG=90°，∴FG=2AF=4，∴AG=在△ADE和△GCE中，∵∠AGF=∠DAE=30°．∠CEG=∠AED，DE=CE，∴△ADE≌△GCE．∴AE=GE∴EF【点拨】本题主要考查了垂径定理，切线的性质和判定，直角三角形的性质，等边三角形的判定和性质，全等三角形的判定和性质，勾股定理，熟练掌握垂径定理，切线的性质和判定，直角三角形的性质，等边三角形的判定和性质，全等三角形的判定和性质是解题的关键．15．(1)见分析(2)OC=【分析】（1）证明∠BCO=∠ACO，推出OE=OB，即可证明AC是⊙O的切线；（2）证明△OBC≌△OEC，利用勾股定理求得AC=10，在Rt△AOE中，利用勾股定理列式计算可求得圆的半径，进一步求解即可．(1)证明：作OE⊥AC，垂足为E，∵AD⊥CO，∴∠ADO=90°，∴∠ADO=∠ABC=90°，∵∠AOD=∠BOC，∴∠DAO=∠BCO，∵∠DAO=∠ACO，∴∠BCO=∠ACO，∵OB⊥BC，OE⊥AC，∵OE=OB，∵OB是半径，∴AC是⊙O的切线；(2)解：∵OBC=∠OEC，∠BCO=∠ACO，OC=CO，∴△OBC≌△OEC，∴BC=EC=6，在Rt△ABC中，10AC=，∴AE=AC−EC=10−6=4，在Rt△AOE中，设半径为R，∵AE2+OE2=OA2，∴42+R2=(8−R)2，∴R=OC=3，∴在Rt△OBC中，OC==【点拨】本题考查了切线的判定和性质，勾股定理，全等三角形的判定和性质，熟练掌握切线的判定和性质是解题的关键．16．(1)见分析(2)①见分析；②DE=4.8【分析】（1）连接OD、BD，求出BD⊥AC，可得AD=DC，根据三角形的中位线得出OD∥BC，推出OD⊥DE，根据切线的判定推出即可；（2）①利用垂径定理作出AD的垂直平分线即可；②根据垂径定理以及勾股定理求得⊙O的半径和FO，再根据中位线中位线定理求得BD，然后根据三角形面积公式即可求解．(1)证明：连接OD，BD，∵AB为⊙O的直径，∴BD⊥AD，又∵AB=BC，△ABC是等腰三角形，∴BD又是AC边上的中线，∴OD是△ABC的中位线，∴OD∥BC，又DE⊥BC，∴DE⊥OD，∵OD是⊙O的半径，∴DE是⊙O的切线；(2)解：①如图，作AD的垂直平分线与☉O相交于点P，点P即为所求．②如图，AD 的垂直平分线与AD 相交于点F ，连接BD ，∵PF ⊥AD ，∴AF =12AD =4， 设☉O 的半径为r ，在Rt △AFO 中，AF 2+FO 2=AO 2，即42+(8−r ) 2=r 2，解得r =5．∴FO =PF −PO =3，∵FO 是△ABD 的中位线，∴BD =2FO =6，∵AB 为⊙O 的直径，∴BD ⊥AC ，又∵AB =BC ，△ABC 是等腰三角形，∴AD =DC =8，∴BC =AB =10，在Rt △BDC 中，S △BDC =12BD ⋅CD =12BC ⋅DE ， ∴DE =4.8．【点拨】本题考查了切线的判定和性质，等腰三角形的性质，垂径定理，勾股定理，三角形中位线等知识点的综合运用．17．(1)见分析【分析】（1）根据圆周角定理可得260BOD BAD ∠=∠=︒，从而得到90ODB ∠=︒ ，即可求证； （2）连接DM ，Rt △BOD 中，根据直角三角形的性质可得 BO =2OD ，从而得到1OD OC ==，BD =DE O 为的直径，可得2DE =，90DME ∠=︒，从而得到BE =1122BDE S BD DE BE DM =⋅=⋅△，可得DM =，再由勾股定理，即可求解．(1)证明：∵∠BOD =2∠BAD ，∴260BOD BAD ∠=∠=︒，又∵30ABD ∠=︒，∴90ODB ∠=︒ ，即OD BD ⊥，又∵OD 为O 的半径，∴直线BD 是O 的切线；(2)解：如图，连接DM ，Rt △BOD 中，30DBO ∠=︒，∴2BO OD OC BC ==+，又1BC =，OD OC =，∴1OD OC ==，∴BD =∵DE O 为的直径，∴2DE =，90DME ∠=︒，在Rt △BDE 中，BE == ∵1122BDE S BD DE BE DM =⋅=⋅△，∴BD DE DM BE ⋅==在Rt △BDM 中，BM = 【点拨】本题主要考查了切线的判定，圆周角定理，直角三角形的性质，勾股定理等知识，熟练掌握切线的判定，圆周角定理，直角三角形的性质，勾股定理是解题的关键． 18．(1)见分析(2)7(1) 连接OD ，得到OAD ADO ∠=∠，利用余角的性质得到B BDF ∠=∠，得出结果；(2) 连接OF ，构造直角三角形，利用勾股定理求解．(1)证明：连接OD ，如图，∵半圆O 的切线DF ，∴90ODF ∠=︒．∴90ADO BDF ∠+∠=︒．∵90C ∠=︒，∴90OAD B ∠+∠=︒．∵OA OD =，∴OAD ADO ∠=∠．∴B BDF ∠=∠．∴BF DF =．(2)解：连接OF ．∵4AO CE ==，AO OE =，∴8OC =．∵9090C ODF ∠=︒=∠=︒，1CF =，∴2222265OF OC CF OD DF =+=+=．又∵4OD =，∴7DF BF ==．【点拨】本题考查切线的性质、等腰三角形的判定以及勾股定理，遇切线连接圆心和切点时解决问题的关键．19．(1)见分析(2)8（1）根据OC ＝OE ，得到∠OCE ＝∠OEC ，再根据∠AOC ＝2∠ACE ，得到∠OCA ＝∠OCE +∠ACE ＝12（∠OCE +∠OEC +∠AOC ）＝11802⨯＝90°，即有OC ⊥AB ，结论得证； （2）利用勾股定理求出AB ，在根据三角形的面积的不同算法可求出OC ，即AE 可求．(1)证明：∵OC ＝OE ，∴∠OCE ＝∠OEC ，∵∠AOC ＝2∠ACE ，∴∠OCA ＝∠OCE +∠ACE ＝12（∠OCE +∠OEC +∠AOC ） ＝11802⨯＝90°， ∴OC ⊥AB ，∴AB 为⊙O 的切线；(2)∵AO ＝20，BO ＝15，∴25AB ， ∵1122OA OB AB OC ⨯⨯=⨯⨯， 即1120152522OC ⨯⨯=⨯⨯， ∴OC ＝12，∴AE ＝OA ﹣OE ＝20﹣12＝8.【点拨】本题考查了切线的判定与性质、勾股定理以及三角形面积的知识，利用勾股定理解直角三角形是解答本题的关键．20．(1)见分析；(2)【分析】（1）根据切线的判定定理证明即可；（2）证明ABO 是等边三角形，利用30所对的直角边等于斜边的一半证明132AE AB ==，再由勾股定理，得BE (1)证明：连接BO ．∵OA OB =，∴OAB OBA ∠=∠．∵AB 平分CAE ∠，∴OAB BAE ∠=∠，∴OBA BAE ∠=∠．∴OB AE ∥，∴18090EBO E ∠=︒-∠=︒，即BE OB ⊥，又∵OB 是O 的半径，∴BE 是O 的切线．(2)解：30ACB ∠=︒，∴60AOB ∠=︒．又∵OA OB =，∴ABO 是等边三角形，∴60OBA ∠=︒，6OA OB AB ===，∴30ABE ∠=︒， ∴132AE AB ==．由勾股定理，得BE =【点拨】本题考查切线的判定定理，等边三角形的判定及性质，30所对的直角边等于斜边的一半，勾股定理，解题的关键是熟练掌握以上知识点．21．(1)见分析(2)8【分析】（1）过O 作OE ⊥AC 于E ，先证Rt △ABO ≌Rt △AEO ，OB ＝OE ，即OE 为圆的半径，即可求证；（2）利用切线的性质可得AB =AE ，再证Rt △BOD ≌Rt △COE ，即有BD ＝CE ＝2，则AC 可求．(1)证明：过O 作OE ⊥AC 于E ．∵AO 平分∠BAC ，且∠ABC ＝90°，OE ⊥AC ，∴OB ＝OE ，即OE 为圆的半径，∴AC 是⊙O 的切线；(2)∵∠ABC ＝90°，OB 为⊙O 半径，∴AB 是⊙O 的切线，又由（1）AC 是⊙O 的切线，∴AB ＝AE ＝6，在Rt △BOD 和Rt △COE 中，OB OE OD OC =⎧⎨=⎩， ∴Rt △BOD ≌Rt △COE ，∴BD ＝CE ＝2，∴AC ＝AE +CE ＝8【点拨】本题考查了切线的判定与性质，角平分线的性质定理，在OE ⊥AC 的条件下证得OE 为圆的半径是解答本题的关键．22．(1)DE 是⊙O 的切线，理由见分析；(2)DE 的长为245． 【分析】（1）连接OD ，根据等边对等角性质和平行线的判定和性质证得OD ⊥DE ，从而证得DE 是⊙O 的切线；（2）由等腰三角形的性质求出BD =CD =8，由勾股定理求出AD 的长，根据三角形的面积得出答案．(1)解：DE 是⊙O 的切线，理由如下：连接OD ，∵OB =OD ，∵AB=AC，∴∠B=∠C，∴∠ODB=∠C，∴OD∥AC，∵DE⊥AC，∴OD⊥DE，∴DE是⊙O的切线；(2)解：连接AD，∵∠ADB=90°，AB=AC，∴BD=CD，∵⊙O的半径为5，BC=16，∴AC=AB=10，CD=8，∴AD= 6，∵S△ADC=12AC•DE=12AD•CD，∴DE=6824105 AD CDAC⋅⨯==．【点拨】本题考查了切线的判定与性质，圆周角定理，等腰三角形的性质和判定，三角形的内角和定理，勾股定理，三角形的面积等知识，掌握切线的判定与性质是解题的关键．23．(1)见分析(2)3【分析】（1）连接OD、CD，由AC为⊙O的直径知△BCD是直角三角形，结合E为BC的中点知∠CDE=∠DCE，由∠ODC=∠OCD且∠OCD+∠DCE=90°可得答案；（2）设⊙O的半径为r，由OD2+DF2=OF2，即r2+42=（r+2）2可得r=3，即可得出答案．(1)解：如图，连接OD、CD．∵AC为⊙O的直径，∴∠ADC=90°，∴∠CDB=90°，即△BCD是直角三角形，∵E为BC的中点，∴∠CDE =∠DCE ，∵OD =OC ，∴∠ODC =∠OCD ，∵∠ACB =90°，∴∠OCD +∠DCE =90°，∴∠ODC +∠CDE =90°，即OD ⊥DE ，∴DE 是⊙O 的切线；(2)解：设⊙O 的半径为r ，∵∠ODF =90°，∴OD 2+DF 2=OF 2，即r 2+42=（r +2）2，解得：r =3，∴⊙O 的半径为3．【点拨】本题主要考查了圆切线的判定与性质，等腰三角形的性质与判定，直角三角形斜边上的中线，勾股定理等等，熟知圆切线的性质与判定是解题的关键．24．(1)60︒(2)见分析【分析】（1）由直径为6，求得⊙O 的周长，再由AC 的长为π，求得AOC ∠的度数．（2）由（1）知60AOC ∠=︒，由于OB OC =，可得1302OBC AOC ∠=∠=︒，再由BC PC =推出30P ∠=︒，从而证得OC CP ⊥，直线PC 与⊙O 相切．(1)解：∵6AB =，∴⊙O 的周长为6π．∵AC 的长为π， ∴1360606AOC ∠=⨯︒=︒． (2)证明：∵AB 为⊙O 的直径，点C 在⊙O 上，∴OB OC =， ∴12OBC OCB AOC ∠=∠=∠．∵60AOC ∠=︒， ∴1302OBC OCB AOC ∠=∠=∠=︒． ∵BC PC =，∴30CBO P ∠=∠=︒．在COP 中，∵60COA ∠=︒，30P ∠=︒，∴180180603090OCP COA P ∠=︒-∠-∠=︒-︒-︒=︒，∴OC CP ⊥，又∵点C 在⊙O 上，∴直线PC 与⊙O 相切．【点拨】本题考查了圆的相关性质，切线的判定，综合运用圆的性质确定相关角度是解题关键．。
圆的切线专题证明题
1、.已知：如图，CB是⊙O的直径,BP是和⊙O相切于点B的切线,⊙O的弦AC平行于OP．(1)求证:AP是⊙O的切线．(2)若∠P=60°,PB=2cm，求AC．2、⊿ABC中,AB=AC，以AB为直径作⊙O交BC于D，D E⊥AC于E。
求证:DE为⊙O的切线3、、如图,AB=BC，以AB为直径的⊙O交AC于D,作D E⊥BC于E.（1）求证：DE为⊙O的切线（2）作DG⊥AB交⊙O于G，垂足为F，∠A=30°。
AB=8，求DG的长4、如图，AB为⊙O的直径，BC切⊙O于B，AC交⊙O于P，CE=BE，E在BC上. 求证：PE是⊙O的切线．APOB5、如图，D是⊙O的直径CA延长线上一点,点B在⊙O上，且AB＝AD＝AO．求证：BD是⊙O的切线；6．如图，在中，，以为直径的分别交、于点、，点在的延长线上，且求证：直线是⊙0的切线；7、如图9，直线n切⊙O于A，点P为直线n上的一点，直线PO交⊙O于C、B,D在线段AP上，连接DB，且AD=DB.（1)判断DB与⊙O的位置关系，并说明理由。
（2）若AD=1，PB=BO，求弦AC的长8、如图10，⊙O直径AB=4，P在AB的延长线上，过P作⊙O切线，切点为C，连接AC。
(1）若∠CPA=30°，求PC的长(2）若P在AB的延长线上运动，∠CPA的平分线交AC于点M，你认为∠CMP 的大小是否发生变化？若变化，请说明理由;若不变化，求出∠CMP的值。
9．如图,MN为⊙O的切线，A为切点，过点A作AP⊥MN,交⊙O的弦BC于点P。
若PA=2cm，PB=5cm，PC=3cm，求⊙O的直径．10．已知：如图,同心圆O，大圆的弦AB=CD，且AB是小圆的切线，切点为E．求证：CD是小圆的切线．11、如图,AB为⊙O的直径，AD平分∠BAC交⊙O于点D，DE⊥AC交AC的延长线于点E，FB是⊙O的切线交AD的延长线于点F. （1）求证：DE是⊙O的切线；（2）若DE=3,⊙O的半径为5，求BF的长。
(完整版)中考数学-圆的切线证明综合试题
专题-------圆的切线证明我们学习了直线和圆的位置关系，就出现了新的一类习题，就是证明一直线是圆的切线.在我们所学的知识范围内，证明圆的切线常用的方法有：一、若直线l 过⊙O 上某一点A ，证明l 是⊙O 的切线，只需连OA ，证明OA⊥l 就行了，简称“连半径，证垂直”，难点在于如何证明两线垂直.例1 如图，在△ABC 中，AB=AC ，以AB 为直径的⊙O 交BC 于D ，交AC 于E ，B 为切点的切线交OD 延长线于F.求证：EF 与⊙O 相切.证明：连结OE ，AD. ∵AB 是⊙O 的直径， ∴AD⊥BC. 又∵AB=BC， ∴∠3=∠4. ∴BD=DE，∠1=∠2. 又∵OB=OE，OF=OF ， ∴△BOF≌△EOF（SAS ）. ∴∠OBF=∠OEF. ∵BF 与⊙O 相切， ∴OB⊥BF. ∴∠OEF=900.∴EF 与⊙O 相切.说明：此题是通过证明三角形全等证明垂直的例2 如图，AD 是∠BAC 的平分线，P 为BC 延长线上一点，且PA=PD.求证：PA 与⊙O 相切.证明一：作直径AE ，连结EC. ∵AD 是∠BAC 的平分线， ∴∠DAB=∠DAC.⌒⌒∵PA=PD， ∴∠2=∠1+∠DAC. ∵∠2=∠B+∠DAB， ∴∠1=∠B. 又∵∠B=∠E， ∴∠1=∠E∵AE 是⊙O 的直径， ∴AC⊥EC，∠E+∠EAC=900. ∴∠1+∠EAC=900. 即OA⊥PA.∴PA 与⊙O 相切.证明二：延长AD 交⊙O 于E ，连结OA ，OE. ∵AD 是∠BAC 的平分线，∴BE=CE，∴OE⊥BC.∴∠E+∠BDE=900. ∵OA=OE， ∴∠E=∠1. ∵PA=PD， ∴∠PAD=∠PDA.又∵∠PDA=∠BDE,∴∠1+∠PAD=900即OA⊥PA.∴PA 与⊙O 相切说明：此题是通过证明两角互余，证明垂直的，解题中要注意知识的综合运用.例3 如图，AB=AC ，AB 是⊙O 的直径，⊙O 交BC 于D ，DM⊥AC 于M求证：DM 与⊙O 相切.证明一：连结OD. ∵AB=AC， ∴∠B=∠C.⌒⌒∵OB=OD，∴∠1=∠B.∴∠1=∠C. ∴OD∥AC. ∵DM⊥AC，∴DM⊥OD.∴DM 与⊙O 相切证明二：连结OD ，AD.∵AB 是⊙O 的直径，∴AD⊥BC.又∵AB=AC,∴∠1=∠2. ∵DM⊥AC，∴∠2+∠4=900∵OA=OD，∴∠1=∠3.∴∠3+∠4=900.即OD⊥DM.∴DM 是⊙O 的切线说明：证明一是通过证平行来证明垂直的.证明二是通过证两角互余证明垂直的，解题中注意充分利用已知及图上已知.例4 如图，已知：AB 是⊙O 的直径，点C 在⊙O 上，且∠CAB=300，BD=OB ，D 在AB 的延长线上.求证：DC 是⊙O 的切线证明：连结OC 、BC.∵OA=OC，∴∠A=∠1=∠300.∴∠BOC=∠A+∠1=600. 又∵OC=OB，∴△OBC 是等边三角形.∴OB=BC.∵OB=BD， ∴OB=BC=BD. ∴OC⊥CD. ∴DC 是⊙O 的切线.说明：此题是根据圆周角定理的推论3证明垂直的，此题解法颇多，但这种方法较好.例5 如图，AB 是⊙O 的直径，CD⊥AB，且OA 2=OD·OP.求证：PC 是⊙O 的切线.证明：连结OC∵OA 2=OD·OP ，OA=OC ， ∴OC 2=OD·OP ，.OCOPOD OC 又∵∠1=∠1， ∴△OCP∽△ODC. ∴∠OCP=∠ODC. ∵CD⊥AB， ∴∠OCP=900. ∴PC 是⊙O 的切线.说明：此题是通过证三角形相似证明垂直的例6 如图，ABCD 是正方形，G 是BC 延长线上一点，AG 交BD 于E ，交CD 于F.求证：CE 与△CFG 的外接圆相切.分析：此题图上没有画出△CFG 的外接圆，但△CFG 是直角三角形，圆心在斜边FG 的中点，为此我们取FG 的中点O ，连结OC ，证明CE⊥OC 即可得解.证明：取FG 中点O ，连结OC.∵ABCD 是正方形，∴BC⊥CD，△CFG 是Rt△∵O 是FG 的中点， ∴O 是Rt△CFG 的外心. ∵OC=OG， ∴∠3=∠G，∵AD∥BC，∴∠G=∠4.∵AD=CD，DE=DE，∠ADE=∠CDE=450，∴△ADE≌△CDE（SAS）∴∠4=∠1，∠1=∠3.∵∠2+∠3=900,∴∠1+∠2=900.即CE⊥OC.∴CE与△CFG的外接圆相切二、若直线l与⊙O没有已知的公共点，又要证明l是⊙O的切线，只需作OA⊥l，A为垂足，证明OA是⊙O的半径就行了，简称：“作垂直；证半径”例7 如图，AB=AC，D为BC中点，⊙D与AB切于E点.求证：AC与⊙D相切.证明一：连结DE，作DF⊥AC，F是垂足.∵AB是⊙D的切线，∴DE⊥AB.∵D F⊥AC，∴∠DEB=∠DFC=900.∵AB=AC，∴∠B=∠C.又∵BD=CD，∴△BDE≌△CDF（AAS）∴DF=DE.∴F在⊙D上.∴AC是⊙D的切线证明二：连结DE，AD，作DF⊥AC，F是垂足.∵AB与⊙D相切，∴DE⊥AB.∵AB=AC，BD=CD，∴∠1=∠2.∴DE=DF.∴F 在⊙D 上.∴AC 与⊙D 相切.说明：证明一是通过证明三角形全等证明DF=DE 的，证明二是利用角平分线的性质证明DF=DE 的，这类习题多数与角平分线有关.例8 已知：如图，AC ，BD 与⊙O 切于A 、B ，且AC∥BD，若∠COD=900.求证：CD 是⊙O 的切线.证明一：连结OA ，OB ，作OE⊥CD，E 为垂足.∵AC，BD 与⊙O 相切， ∴AC⊥OA，BD⊥OB. ∵AC∥BD，∴∠1+∠2+∠3+∠4=1800. ∵∠COD=900，∴∠2+∠3=900，∠1+∠4=900. ∵∠4+∠5=900. ∴∠1=∠5.∴Rt△AOC∽Rt△BDO.∴.ODOCOB AC = ∵OA=OB， ∴.ODOCOA AC = 又∵∠CAO=∠COD=900， ∴△AOC∽△ODC，∴∠1=∠2.又∵OA⊥AC，OE⊥CD, ∴OE=OA. ∴E 点在⊙O 上. ∴CD 是⊙O 的切线.证明二：连结OA ，OB ，作OE⊥CD 于E ，延长DO 交CA 延长线于F.∵AC，BD 与⊙O 相切，O∵AC∥BD，∴∠F=∠BDO.又∵OA=OB，∴△AOF≌△BOD（AAS ）∴OF=OD.∵∠COD=900，∴CF=CD，∠1=∠2.又∵OA⊥AC，OE⊥CD，∴OE=OA.∴E 点在⊙O 上.∴CD 是⊙O 的切线.证明三：连结AO 并延长，作OE⊥CD 于E ，取CD 中点F ，连结OF.∵AC 与⊙O 相切，∴AC⊥AO.∵A C∥BD，∴AO⊥BD.∵BD 与⊙O 相切于B ，∴AO 的延长线必经过点B.∴AB 是⊙O 的直径.∵AC∥BD，OA=OB ，CF=DF ，∴OF∥AC，∴∠1=∠COF.∵∠COD=900，CF=DF ，∴.CF CD OF ==21∴∠2=∠COF.∴∠1=∠2.∵OA⊥AC，OE⊥CD，∴OE=OA.∴E 点在⊙O 上.∴CD 是⊙O 的切线说明：证明一是利用相似三角形证明∠1=∠2，证明二是利用等腰三角形三线合一证明∠1=∠2.证明三是利用梯形的性质证明∠1=∠2，这种方法必需先证明A 、O 、B 三点共线.此题较难，需要同学们利用所学过的知识综合求解.以上介绍的是证明圆的切线常用的两种方法供同学们参考.以下是武汉市2007----2010中考题汇编：（2007中考）22．(本题8分)如图，等腰三角形ABC 中，AC ＝BC ＝10，AB ＝12。
中考复习专题——圆切线证明
中考复习专题——圆切线证明中考复习专题--------圆的切线的判定与性质知识考点：1、掌握切线的判定及其性质的综合运用，在涉及切线问题时，常连结过切点的半径，切线的判定常用以下两种方法：一是连半径证垂直，二是作垂线证半径。
2、掌握切线长定理的灵活运用，掌握三角形和多边形的内切圆，三角形的内心。
精典例题：一、若直线l过⊙O上某一点A，证明l是⊙O的切线，只需连OA，证明OA⊥l就行了，简称“连半径，证垂直”，难点在于如何证明两线垂直.例1如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于D，交AC于E，B为切点的切线交OD延长线于F.求证：EF与⊙O相切.例2 如图，AD是∠BAC的平分线，P为BC延长线上一点，且PA=PD.求证：PA与⊙O相切.例3 如图，AB=AC，AB是⊙O的直径，⊙O交BC 于D，DM⊥AC于M求证：DM与⊙O相切.例4 如图，已知：AB是⊙O的直径，点C在⊙O上，且∠CAB=300，BD=OB，D在AB的延长线上.求证：DC是⊙O的切线例 5 如图，AB是⊙O的直径，CD⊥AB，且OA2=OD·OP.求证：PC是⊙O的切线.例6 如图，ABCD是正方形，G是BC延长线上一点，AG交BD于E，交CD于F.求证：CE与△CFG的外接圆相切.二、若直线l与⊙O没有已知的公共点，又要证明l是⊙O的切线，只需作OA⊥l，A为垂足，证明OA是⊙O 的半径就行了，简称：“作垂直；证半径”例7 如图，AB=AC，D为BC中点，⊙D与AB切于E点.求证：AC与⊙D相切.例8 已知：如图，AC，BD与⊙O切于A、B，且AC ∥BD，若∠COD=900.求证：CD是⊙O的切线.[习题练习]例1如图，AB是⊙O的弦（非直径），C、D是AB上两点，并且OC=OD，求证：AC=BD．例2已知：如图，在△ABC中，AB=AC，以AB为直径的⊙O与BC交于点D，与AC•交于点E，求证：△DEC为等腰三角形．例3如图，AB是⊙O的直径，弦AC与AB成30°角，CD 与⊙O切于C，交AB•的延长线于D，求证：AC=CD．例4如图20-12，BC为⊙O的直径，AD⊥BC，垂足为D，AB AF，BF和AD交于E，求证：AE=BE．例5如图，AB是⊙O的直径，以OA为直径的⊙O1与⊙O2的弦相交于D，DE⊥OC，垂足为E．（1）求证：AD=DC．（2）求证：DE是⊙O1的切线．AB CDE F G O例6如图，已知直线MN 与以AB 为直径的半圆相切于点C ，∠A=28°．（1）求∠ACM 的度数．（2）在MN 上是否存在一点D ，使AB ·CD=AC ·BC ，说明理由．例7如图，在Rt △ABC 中，∠C=90°，AC=5，BC=12，⊙O 的半径为3．（1）若圆心O 与C 重合时，⊙O 与AB 有怎样的位置关系？（2）若点O 沿CA 移动，当OC 等于多少时，⊙O 与AB 相切？19.如图，Rt△ABC 内接于⊙O，AC=BC ，∠BAC 的平分线AD 与⊙0交于点D ，与BC 交于点E ，延长BD ，与AC 的延长线交于点F ，连结CD ，G 是CD 的中点，连结0G ．(1)判断0G 与CD 的位置关系，写出你的结论并证明；(2)求证：AE=BF ；（3）若3(2OG DE ⋅=-，求⊙O 的面积。
圆切线性质与判定证明题
1圆切线性质与判定证明题1、如图，AB 为⊙O 的直径，PC 切⊙O 于C ，且AC ∥OP ，试判断段直线PB 与⊙O 的位置关系，并说明理由。
2、 如图，Rt ΔABC 中，∠ACB=90°，以BC 为直径作半圆O 交AB 边于点E ，D 为AC 中点，连接DE ，判断DE 与半⊙O 的位置关系，并说明理由。
3、如图，以Rt ΔABC 的直角边AB 为直径作圆O 交斜边于点D,作OE ∥BC 交AC 于E ，连接DE.求证：DE 是⊙O 的切线。
4、如图，已知AB 为⊙O 的直径，C 、D 是直径AB 同侧圆周上两点，且弧CD=弧BD ，过D 作DE⊥AC 于点E.求证：DE 是⊙O 的切线.5、 已知：如图，△ABC 中，AB=AC ，以AB 为直径的⊙O 交BC 于点P ，P D ⊥AC 于点D 。
（1）求证：PD 是⊙O 的切线。
（2）若∠CAB=120°，AB=2，求BC 的长6、 如图，AB 是⊙O 直径，AD 是弦，∠DAB=22.5°，延长AB 到C ，使得∠ACD=45°.（1）求证：CD 是⊙O 的切线；（2）若AB=22，求BC 的长。
2 7、 如图，四边形ABCD 内接于⊙O ，BD 是⊙O 直径，A E ⊥CD ，垂足为E ，DA 平分∠BDE 。
（1）求证：AE 是⊙O 的切线；（2）若∠DBC=30°，DE=1cm,求BD 的长。
8、 如图，在△ABC 中，∠B=60°，⊙O 是△ABC 的外接圆，过点A 作⊙O 的切线，交CO 的延长线于点P ，CP 交⊙O 于点D 。
（1）求证：AP=AC（2）若AC=3，求PC 的长9、 如图，点A 、B 在⊙O 上，直线AC 是⊙O 的切线，OC ⊥OB ，连接AB 交OC 于点D 。
（1）求证：AC=CD（2）若AC=2，OD 的长10、如图，在⊙O 中，直径AB 与弦CD 相交于点P ，∠CAB=40°，∠APD=65°.（1）求∠B 的大小。
中考数学总复习《圆的切线的证明》专项提升练习题-附答案
中考数学总复习《圆的切线的证明》专项提升练习题-附答案学校：___________班级：___________姓名：___________考号：___________1．如图，O为菱形 ABCD对角线上一点，⊙O与BC相切于点M．求证：CD与⊙O相切．2．如图，在梯形ABCD中，AD∥BC，∠C=90°，AD+BC=AB，以AB为直径作⊙O，求证：CD是⊙O的切线．3．在Rt△ABC中，∠ACB=90°，BE平分∠ABC，D是边AB上一点，以BD为直径的⊙O经过点E，且交BC 于点F．（1）求证：AC是⊙O的切线；（2）若BF=6，⊙O的半径为5，求CE的长．4．如图，AB是⊙O的直径，弦DE垂直平分半径OA，C为垂足，DE＝3，连接DB，过点E作EM∥BD，交BA 的延长线于点M．（1）求⊙O的半径；（2）求证：EM是⊙O的切线；（3）若弦DF与直径AB相交于点P，当∠APD＝45º时，求图中阴影部分的面积．5．如图，在Rt△ABC中∠C=90°，BD平分∠ABC，交AC于点D，点O是AB边上的点，以BD为弦的⊙O 交AB于点E．（1）求证：AC是⊙O的切线；（2）若∠A=30°，OB=1求阴影部分的面积．6．如图，在Rt△ABC中，∠ACB＝90°，E是BC的中点，以AC为直径的⊙O与AB边交于点D，连接DE．（1）求证：DE是⊙O的切线；（2）若CD＝3cm，DE＝2.5cm，求⊙O直径的长．7．如图，AB是⊙O的直径，点C、E在⊙O上，AC平分∠BAE，CM⊥AE于点D．求证：CM是⊙O的切线．8．如图，△ABC是⊙O的内接三角形，D是圆外一点，连接DA，∠DAC=∠ABC连接DC交⊙O于点E．（1）求证：AD是⊙O的切线；（2）若AD=4，E是CD的中点，求CE的长度．9．如图所示，AB是⊙O的直径，AD是弦，∠DAB=20°，延长AB到点C，使得∠ACD=50°，求证：CD是⊙O的切线．10．如图，在⊙O中，直径AB垂直于弦CD，垂足为E，连接AC，将△ACE沿AC翻折得到△ACF，直线FC与直线AB相交于点G．（1）直线FC与⊙O有何位置关系？并说明理由；（2）若OB＝BG＝2，求CD的长．二、综合题11．如图，AB是⊙O的弦，过AB的中点E作EC⊥OA，垂足为C，过点B作直线BD交CE的延长线于点D，使得DB=DE．（1）求证：BD是⊙O的切线；（2）若AB=12，DB=5，求△AOB的面积．⌢的中点，EF∥12．如图，AB是⊙O的直径，AB=6，OC⊥AB，OC=5，BC与⊙O交于点D，点E是BDBC，交OC的延长线于点F.（1）求证：EF是⊙O的切线；（2）CG∥OD，交AB于点G，求CG的长.13．如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD.（1）求证：CD是⊙O的切线；（2）过点B作⊙O的切线交CD的延长线于点E，若BC=12，OBBE = 23，求BE的长.14．如图，△BEF内接于⊙O，BE=BF，BO的延长线交EF于点D.C是⊙O外一点，连接OC，BC，OC⊥BE 于点A.已知OA=2，AB=4，AC=8.（1）求证：BC是⊙O的切线.（2）求EF的长.15．如图，△ABC内接于⊙O，AD平分∠BAC交BC边于点E，交⊙O于点D，过点A作AF⊥BC于点F，设⊙O的直径为d，AF＝h.（1）过点D作直线MN∥BC，求证：MN是⊙O的切线；（2）若AB＝4，AC＝3，求dh的值.16．如图，AB是⊙O的直径，点C、D在⊙O上，且AC平分∠BAD，点E为AB的延长线上一点，且∠ECB=∠CAD．（1）填空：∠ACB= ，理由是（2）求证：CE与⊙O相切（3）若AB=6，CE=4，求AD的长17．如图，AB为⊙O的直径，点C在⊙O上，AD⊥CD于点D，且AC平分∠DAB，求证：（1）直线DC是⊙O的切线；（2）AC2=2AD•AO．18．如图，在Rt△ABC中，∠B＝90°，∠BAC的平分线交BC于点D，E为AB上的一点，DE＝DC，以D为圆心，DB长为半径作⊙D，AB＝5，EB＝3.（1）求证：AC是⊙D的切线；（2）求线段AC的长．19．如图，已知ΔABC内接于⊙O，AB为⊙O的直径，BD⊥AB，交AC的延长线于点D．（1）若E是BD的中点，连结CE，试判断CE与⊙O的位置关系．（2）若AC=3CD，求∠A的大小．20．如图，四边形ABCD内接于⊙O，点E在CB的延长线上，连接AC，AE，∠ACB=∠BAE=45°（1）求证：AE是⊙O的切线；（2）若 AB=AD，AC=2 √2，tan∠ADC=3，求CD的长．21．如图，AB是⊙O的直径，BM切⊙O于点B，点P是⊙O上的一个动点（点P不与A，B两点重合），连接AP，过点O作OQ∥AP交BM于点Q，过点P作PE⊥AB于点C，交QO的延长线于点E，连接PQ，OP，AE.（1）判断直线PQ与⊙O的关系；（2）若直径AB的长为4.当四边形AEOP为菱形时，求PE的长.答案1．证明：连接OM，过点O作ON⊥CD于垂足为N∵⊙O与BC相切于点M∴OM⊥BC，OM为半径∴∠OMC=∠ONC=90°∵AC是菱形ABCD的对角线∴∠ACB=∠ACD∵OC=OC∴△OMC≌△ONC（AAS）∴ON=OM=半径，∠ONC=90°∴CD与⊙O相切．2．证明：过点O作OE⊥CD于点E∵在梯形ABCD中，AD∥BC，∠C=90°∴AD⊥CD，BC⊥CD∴AD∥OE∥BC∵OA=OB∴OE是梯形ABCD的中位线（AD+BC）∴OE= 12∵AD+BC=AB∴OE= 1AB2∵以AB为直径作⊙O．∴直线CD是⊙O的切线．3．解：（1）连接OE．∵OE=OB∴∠OBE=∠OEB∵BE平分∠ABC∴∠OBE=∠EBC∴∠EBC=∠OEB∴OE∥BC∴∠OEA=∠C∵∠ACB=90°∴∠OEA=90°∴AC是⊙O的切线；（2）连接OE、OF，过点O作OH⊥BF交BF于H由题意可知四边形OECH为矩形∴OH=CE∵BF=6∴BH=3在Rt△BHO中，OB=5∴OH=4∴CE=4．4．（1）连结OE，如图：∵DE垂直平分半径OA∴OC=∴∠OEC=30°∴（2）由（1）知：∠AOE=60°∴∴∠BDE=60°∵BD∥ME∴∠MED=∠BDE=60°∴∠MEO=90°∴EM是⊙O的切线。
2024年中考数学复习重难点题型训练—圆的相关证明与计算(含答案解析)
2024年中考数学复习重难点题型训练—圆的相关证明与计算（含答案解析）类型一基本性质有关的1.(2022·湖南省郴州市)如图，在△ABC中，AB=AC.以AB为直径的⊙O与线段BC交于点D，过点D作DE⊥AC，垂足为E，ED的延长线与AB的延长线交于点P．(1)求证：直线PE是⊙O的切线；(2)若⊙O的半径为6，∠P=30°，求CE的长．【答案】(1)连接OD，根据AB=AC，OB=OD，得∠ACB=∠ODB，从而OD//AC，由DE⊥AC，即可得PE⊥OD，故PE是⊙O的切线；(2)连接AD，连接OD，由DE⊥AC，∠P=30°，得∠PAE=60°，又AB=AC，可得△ABC 是等边三角形，即可得BC=AB=12，∠C=60°，而AB是⊙O的直径，得∠ADB=90°，可得BD=CD=12BC=6，在Rt△CDE中，即得CE的长是3．本题考查圆的综合应用，涉及圆的切线，等腰三角形性质及应用，含特殊角的直角三角形三边关系等，解题的关键是判定△ABC是等边三角形．2.(2022·辽宁省盘锦市)如图，△ABC内接于⊙O，∠ABC=45°，连接AO并延长交⊙O于点D，连接BD，过点C作CE//AD与BA的延长线交于点E．(1)求证：CE与⊙O相切；(2)若AD=4，∠D=60°，求线段AB，BC的长．【答案】(1)连接OC，根据圆周角定理得∠AOC=90°，再根据AD//EC，可得∠OCE=90°，从而证明结论；(2)过点A作AF⊥EC交EC于F，由AD是圆O的直径，得∠ABD=90°，又AD=4，60°，即得AB=3BD=23，根据∠ABC=45°，知△ABF是等腰直角三角形，AF=BF=2AB= 6，又△AOC是等腰直角三角形，OA=OC=2，得AC=22，故CF=AC2−AF2=2，从而BC=BF+CF=6+2．本题主要考查了圆周角定理，切线的判定与性质，含30°角的直角三角形的性质等知识，作辅助线构造特殊的直角三角形是解题的关键．3.（2021·山东临沂市·中考真题）如图，已知在⊙O中，＝＝，OC与AD相交于点AB BC CDE．求证：（1）AD∥BC（2）四边形BCDE为菱形．【答案】（1）见解析；（2）见解析【分析】（1）连接BD ，根据圆周角定理可得∠ADB=∠CBD ，根据平行线的判定可得结论；（2）证明△DEF ≌△BCF ，得到DE=BC ，证明四边形BCDE 为平行四边形，再根据 BCCD =得到BC=CD ，从而证明菱形．【详解】解：（1）连接BD ，∵ AB BCCD ==，∴∠ADB=∠CBD ，∴AD ∥BC ；（2）连接CD ，∵AD ∥BC ，∴∠EDF=∠CBF ，∵ BCCD =，∴BC=CD ，∴BF=DF ，又∠DFE=∠BFC ，∴△DEF ≌△BCF （ASA ），∴DE=BC ，∴四边形BCDE 是平行四边形，又BC=CD ，∴四边形BCDE 是菱形．【点睛】本题考查了垂径定理，圆周角定理，弧、弦、圆心角的关系，全等三角形的判定和性质，菱形的判定，解题的关键是合理运用垂径定理得到BF=DF ．4.（2021·四川南充市·中考真题）如图，A ，B 是O 上两点，且AB OA =，连接OB 并延长到点C ，使BC OB =，连接AC ．（1）求证：AC 是O 的切线．（2）点D ，E 分别是AC ，OA 的中点，DE 所在直线交O 于点F ，G ，4OA =，求GF 的长．【答案】（1）见解析；（2）【分析】（1）先证得△AOB 为等边三角形，从而得出∠OAB=60°，利用三角形外角的性质得出∠C=∠CAB=30°，由此可得∠OAC=90°即可得出结论；（2）过O 作OM ⊥DF 于M ，DN ⊥OC 于N ，利用勾股定理得出AC=30°的直角三角形的性质得出DN ，再根据垂径定理和勾股定理即可求出GF 的长．【详解】（1）证明：∵AB=OA ，OA=OB∴AB=OA=OB∴△AOB 为等边三角形∴∠OAB=60°，∠OBA=60°∵BC=OB∴BC=AB∴∠C=∠CAB又∵∠OBA=60°=∠C+∠CAB∴∠C=∠CAB=30°∴∠OAC=∠OAB+∠CAB=90°∴AC 是⊙O 的切线；（2）∵OA=4∴OB=AB=BC=4∴OC=8∴AC=∵D 、E 分别为AC 、OA 的中点，∴OE//BC ，DC=过O 作OM ⊥DF 于M ，DN ⊥OC 于N则四边形OMDN 为矩形∴DN=OM在Rt △CDN 中，∠C=30°，∴DN=12DC=∴OM=3连接OG ，∵OM ⊥GF∴GF=2MG=222OG OM -=()22243-=213【点睛】本题考查了切线的判定、垂径定理、等边三角形的性质和判定，熟练掌握相关的知识是解题的关键．5.（2021·安徽中考真题）如图，圆O 中两条互相垂直的弦AB ，CD 交于点E ．（1）M 是CD 的中点，OM ＝3，CD ＝12，求圆O 的半径长；（2）点F 在CD 上，且CE ＝EF ，求证：AF BD ⊥．【答案】（1）35；（2）见解析．【分析】（1）根据M 是CD 的中点，OM 与圆O 直径共线可得OM CD ⊥，OM 平分CD ，则有6MC =，利用勾股定理可求得半径的长；（2）连接AC ，延长AF 交BD 于G ，根据CE EF =，AE FC ⊥，可得AF AC =，12∠=∠，利用圆周角定理可得2D ∠=∠，可得1D ∠=∠，利用直角三角形的两锐角互余，可证得90AGB ∠=︒，即有AF BD ⊥．【详解】（1）解：连接OC ，∵M 是CD 的中点，OM 与圆O 直径共线∴OM CD ⊥，OM 平分CD ，90OMC ∴∠=︒12CD = 6MC ∴=．在Rt OMC △中．OC ===∴圆O 的半径为（2）证明：连接AC ，延长AF 交BD 于G ．CE EF = ，AE FC⊥AF AC∴=又CE EF= 12∠∠∴= BCBC = 2D∴∠=∠1D∴∠=∠中在Rt BED∠+∠=︒90D B∴∠+∠=︒B190AGB∴∠=︒90∴⊥AF BD【点睛】本题考查了垂径定理，圆周角定理，直角三角形的两锐角互余，勾股定理等知识点，熟练应用相关知识点是解题的关键．∠是 AD所对的圆周角，6.（2021·浙江中考真题）如图，已知AB是⊙O的直径，ACD∠=︒．30ACD∠的度数；（1）求DABAB=，求DF的（2）过点D作DE AB⊥，垂足为E，DE的延长线交⊙O于点F．若4长．【答案】（1）60︒；（2）23【分析】（1）连结BD ，根据圆周角性质，得B ACD ∠=∠；根据直径所对圆周角为直角、直角三角形两锐角互余的性质计算，即可得到答案；（2）根据含30°角的直角三角形性质，得12AD AB =；根据垂径定理、特殊角度三角函数的性质计算，即可得到答案．【详解】（1）连结BD ，30ACD ∠=︒30B ACD \Ð=Ð=°AB Q 是O 的直径，90ADB ∴∠=︒，9060DAB B ∴∠=︒-∠=︒（2）90ADB ∠=︒ ，30B ∠=︒，4AB =∴122AD AB ==60DAB ∠=︒ ，DE AB ⊥，且AB 是直径sin 60EF DE AD︒∴===2DF DE =∴=．【点睛】本题考查了圆、含30°角的直角三角形、三角函数的知识；解题的关键是熟练掌握圆周角、垂径定理、含30°角的直角三角形、三角函数、直角三角形两锐角互余的性质，从而完成求解．7.（2021·湖南中考真题）如图，ABC 是O 的内接三角形，AC 是O 的直径，点D 是 BC的中点，//DE BC 交AC 的延长线于点E ．（1）求证：直线DE 与O 相切；（2）若O 的直径是10，45A ∠=︒，求CE 的长．【答案】（1）见解析；（2）5CE =．【分析】（1）连接OD ，由点D 是 BC的中点得OD ⊥BC ，由DE//BC 得OD ⊥DE ，由OD 是半径可得DE 是切线；（2）证明△ODE 是等腰直角三角形，可求出OE 的长，从而可求得结论．【详解】解：（1）连接OD 交BC 于点F ，如图，∵点D 是 BC的中点，∴OD ⊥BC ，∵DE//BC∴OD ⊥DE∵OD 是O 的半径∴直线DE 与O 相切；（2）∵AC 是O 的直径，且AB=10,∴∠ABC=90°，152OC OA AB ===∵OD ⊥BC∴∠OFC=90°∴OD//AB 45BAC ∠=︒∴45DOE ∠=︒∵90ODE ∠=︒∴45OED ∠=∴5DE OD OC ===由勾股定理得，OE =∴5CE OE OC =-=．【点睛】此题主要考查了切线的判定与性质的综合运用，熟练掌握切线的判定与性质是解答此题的关键．8.（2021·湖南张家界市·中考真题）如图，在Rt AOB 中，90∠=︒ABO ，30OAB ∠=︒，以点O 为圆心，OB 为半径的圆交BO 的延长线于点C ，过点C 作OA 的平行线，交O 于点D ，连接AD ．（1）求证：AD 为O 的切线；（2）若2OB =，求弧CD 的长．【答案】（1）见解析；（2）23π【分析】（1）连接OB ，先根据直角三角形的性质得到∠AOB=60°，再运用平行线的性质结合已知条件可得60AOD ∠=︒，再证明AOB AOD △≌△可得90ADO ABO ∠=∠=︒即可；（2）先求出∠COD ，然后再运用弧长公式计算即可．【详解】（1）证明：连接OD∵30OAB ∠=︒，90B ∠=︒∴60AOB ∠=︒又∵//CD AO∴60C AOB ∠=∠=︒∴2120BOD C ∠=∠=︒∴60AOD ∠=︒又∵,OB OD AO AO==∴()AOB AOD SAS ≌∴90ADO ABO ∠=∠=︒又∵点D 在O 上∴AD 是O 的切线；（2）∵120BOD ∠=︒∴60COD ∠=︒∴602223603l ππ=⨯⨯=．【点睛】本题主要考查了圆的切线的证明、弧长公式等知识点，掌握圆的切线的证明方法成为解答本题的关键．9.（2020•齐齐哈尔）如图，AB 为⊙O 的直径，C 、D 为⊙O 上的两个点，AC=CD =DB ，连接AD ，过点D 作DE ⊥AC 交AC 的延长线于点E ．（1）求证：DE 是⊙O 的切线．（2）若直径AB ＝6，求AD 的长．【分析】（1）连接OD ，根据已知条件得到∠BOD =13×180°＝60°，根据等腰三角形的性质得到∠ADO＝∠DAB＝30°，得到∠EDA＝60°，求得OD⊥DE，于是得到结论；（2）连接BD，根据圆周角定理得到∠ADB＝90°，解直角三角形即可得到结论．【解析】（1）证明：连接OD，=CD =DB ，∵AC∴∠BOD=13×180°＝60°，=DB ，∵CD∴∠EAD＝∠DAB=12∠BOD＝30°，∵OA＝OD，∴∠ADO＝∠DAB＝30°，∵DE⊥AC，∴∠E＝90°，∴∠EAD+∠EDA＝90°，∴∠EDA＝60°，∴∠EDO＝∠EDA+∠ADO＝90°，∴OD⊥DE，∴DE是⊙O的切线；（2）解：连接BD，∵AB为⊙O的直径，∴∠ADB＝90°，∵∠DAB＝30°，AB＝6，∴BD=12AB＝3，∴AD=62−32=33．10.（2020•深圳）如图，AB为⊙O的直径，点C在⊙O上，AD与过点C的切线互相垂直，垂足为D．连接BC并延长，交AD的延长线于点E．（1）求证：AE＝AB；（2）若AB＝10，BC＝6，求CD的长．【分析】（1）证明：连接AC、OC，如图，根据切线的性质得到OC⊥CD，则可判断OC∥AD，所以∠OCB＝∠E，然后证明∠B＝∠E，从而得到结论；（2）利用圆周角定理得到∠ACB＝90°，则利用勾股定理可计算出AC＝8，再根据等腰三角形的性质得到CE＝BC＝6，然后利用面积法求出CD的长．【解析】（1）证明：连接AC、OC，如图，∵CD为切线，∴OC⊥CD，∴CD⊥AD，∴OC∥AD，∴∠OCB＝∠E，∵OB＝OC，∴∠OCB＝∠B，∴∠B＝∠E，∴AE＝AB；（2）解：∵AB为直径，∴∠ACB＝90°，∴AC=102−62=8，∵AB＝AE＝10，AC⊥BE，∴CE＝BC＝6，∵12CD•AE=12AC•CE，∴CD=6×810=245．11.（2020•陕西）如图，△ABC是⊙O的内接三角形，∠BAC＝75°，∠ABC＝45°．连接AO并延长，交⊙O于点D，连接BD．过点C作⊙O的切线，与BA的延长线相交于点E．（1）求证：AD∥EC；（2）若AB＝12，求线段EC的长．【分析】（1）连接OC，由切线的性质可得∠OCE＝90°，由圆周角定理可得∠AOC＝90°，可得结论；（2）过点A作AF⊥EC交EC于F，由锐角三角函数可求AD＝83，可证四边形OAFC是正方形，可得CF＝AF＝43，由锐角三角函数可求EF＝12，即可求解．【解析】证明：（1）连接OC，∵CE与⊙O相切于点C，∴∠OCE＝90°，∵∠ABC＝45°，∴∠AOC＝90°，∵∠AOC+∠OCE＝180°，∴∴AD∥EC（2）如图，过点A作AF⊥EC交EC于F，∵∠BAC＝75°，∠ABC＝45°，∴∠ACB＝60°，∴∠D＝∠ACB＝60°，∴sin∠ADB=AB AD==83，∴AD=∴OA＝OC＝43，∵AF⊥EC，∠OCE＝90°，∠AOC＝90°，∴四边形OAFC是矩形，又∵OA＝OC，∴四边形OAFC是正方形，∴CF＝AF＝43，∵∠BAD＝90°﹣∠D＝30°，∴∠EAF＝180°﹣90°﹣30°＝60°，∵tan∠EAF=EF AF=3，∴EF=3AF＝12，∴CE＝CF+EF＝12+43．类型二与三角形全等、相似有关的12.(2022·辽宁省营口市)如图，在△ABC中，AB=AC，以AB为直径作⊙O与AC交于点E，过点A作⊙O的切线交BC的延长线于点D．(1)求证：∠D=∠EBC；(2)若CD=2BC，AE=3，求⊙O的半径．【答案】(1)根据切线的性质可得∠DAO=90°，从而可得∠D+∠ABD=90°，根据直径所对的圆周角是直角可得∠BEC=90°，从而可得∠ACB+∠EBC=90°，然后利用等腰三角形的性质可得∠ACB=∠ABC，从而利用等角的余角相等即可解答；(2)根据已知可得BD=3BC，然后利用(1)的结论可得△DAB∽△BEC，从而利用相似三角形的性质可得AB=3EC，然后根据AB=AC，进行计算即可解答．本题考查了圆周角定理，等腰三角形的性质，切线的性质，相似三角形的判定与性质，熟练掌握切线的性质，以及相似三角形的判定与性质是解题的关键．13.（2022·北部湾）如图，在△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作DE⊥AB，垂足为E，延长BA交⊙O于点F.（1）求证：DE是⊙O的切线（2）若AE DE=23，AF=10，求⊙O的半径.【答案】（1）证明：连接OD；∵OD=OC，∴∠C=∠ODC，∵AB=AC，∴∠B=∠C，∴∠B=∠ODC，∴OD∥AB，∴∠ODE=∠DEB；∵DE⊥AB，∴∠DEB=90°，∴∠ODE=90°，即DE⊥OD，∴DE是⊙O的切线（2）解：连接CF，由（1）知OD⊥DE，∵DE⊥AB，∴OD∥AB，∵OA=OC，∴BD=CD，即OD是△ABC的中位线，∵AC是⊙O的直径，∴∠CFA=90°，∵DE⊥AB，∴∠BED=90°，∴∠CFA=∠BED=90°，∴DE∥CF，∴BE=EF，即DE是△FBC的中位线，∴CF=2DE，∵AE DE=23，∴设AE=2x，DE=3k，CF=6k，∵AF=10，∴BE=EF=AE+AF=2k+10，∴AC=BA=EF+AE=4k+10，在Rt△ACF中，由勾股定理，得AC2=AF2+CF2，即(4k+10)2=102+(6k)2，解得：k=4，∴AC=4k+10=4×4+10=26，∴OA=13，即⊙O的半径为13.【知识点】平行线的判定与性质；等腰三角形的性质；圆周角定理；切线的判定；三角形的中位线定理【解析】【分析】（1）连接OD ，根据等腰三角形的性质可得∠C=∠ODC ，∠B=∠C ，则∠B=∠ODC ，推出OD ∥AB ，由平行线的性质可得∠ODE=∠DEB=90°，即DE ⊥OD ，据此证明；（2）连接CF ，由（1）知OD ⊥DE ，则OD ∥AB ，易得OD 是△ABC 的中位线，根据圆周角定理可得∠CFA=90°，根据垂直的概念可得∠BED=90°，则DE ∥CF ，推出DE 是△FBC的中位线，得CF=2DE ，设AE=2x ，DE=3k ，CF=6k ，则BE=EF=2k+10，AC=BA=4k+10，根据勾股定理可得k 的值，然后求出AC 、OA ，据此可得半径.14.（2021·江苏无锡市·中考真题）如图，四边形ABCD 内接于O ，AC 是O 的直径，AC 与BD 交于点E ，PB 切O 于点B ．（1）求证：PBA OBC ∠=∠；（2）若20PBA Ð=°，40ACD ∠=︒，求证：OAB CDE V V ∽．【答案】（1）见详解；（2）见详解【分析】（1）由圆周角定理的推论，可知∠ABC=90°，由切线的性质可知∠OBP=90°，进而即可得到结论；（2）先推出20OCB OBC ∠=∠=︒，从而得∠AOB=40°，继而得∠OAB=70°，再推出∠CDE=70°，进而即可得到结论．【详解】证明：（1）∵AC 是O 的直径，∴∠ABC=90°，∵PB 切O 于点B ，∴∠OBP=90°，∴90PBA ABO OBC ABO ∠+∠=∠+∠=︒，∴PBA OBC ∠=∠；（2）∵20PBA Ð=°，PBA OBC ∠=∠，∴20OBC ∠=︒，∵OB=OC ，∴20OCB OBC ∠=∠=︒，∴∠AOB=20°+20°=40°，∵OB=OA ，∴∠OAB=∠OBA=(180°-40°)÷2=70°，∴∠ADB=12∠AOB=20°，∵AC 是O 的直径，∴∠ADC=90°，∴∠CDE=90°-20°=70°，∴∠CDE=∠OAB ，∵40ACD ∠=︒，∴40ACD AOB ∠=∠=︒，∴OAB CDE V V ∽．【点睛】本题主要考查圆的性质以及相似三角形的判定定理，掌握圆周角定理的推论，相似三角形的判定定理，切线的性质定理，是解题的关键．15.（2020•衢州）如图，△ABC 内接于⊙O ，AB 为⊙O 的直径，AB ＝10，AC ＝6，连结OC ，弦AD分别交OC，BC于点E，F，其中点E是AD的中点．（1）求证：∠CAD＝∠CBA．（2）求OE的长．【分析】（1）利用垂径定理以及圆周角定理解决问题即可．（2）证明△AEC∽△BCA，推出CE AC=AC AB，求出EC即可解决问题．【解析】（1）证明：∵AE＝DE，OC是半径，=CD ，∴AC∴∠CAD＝∠CBA．（2）解：∵AB是直径，∴∠ACB＝90°，∵AE＝DE，∴OC⊥AD，∴∠AEC＝90°，∴∠AEC＝∠ACB，∴△AEC∽△BCA，∴CE AC=AC AB，∴CE6=610，∴CE＝3.6，∵OC=12AB＝5，∴OE＝OC﹣EC＝5﹣3.6＝1.4．16.（2020•铜仁市）如图，AB是⊙O的直径，C为⊙O上一点，连接AC，CE⊥AB于点E，D 是直径AB延长线上一点，且∠BCE＝∠BCD．（1）求证：CD是⊙O的切线；（2）若AD＝8，BE CE=12，求CD的长．【分析】（1）连接OC，根据圆周角定理得到∠ACB＝90°，根据余角的性质得到∠A＝∠ECB，求得∠A＝∠BCD，根据等腰三角形的性质得到∠A＝∠ACO，等量代换得到∠ACO＝∠BCD，求得∠DCO＝90°，于是得到结论；（2）设BC＝k，AC＝2k，根据相似三角形的性质即可得到结论．【解析】（1）证明：连接OC，∵AB是⊙O的直径，∴∠ACB＝90°，∵CE⊥AB，∴∠CEB＝90°，∴∠ECB+∠ABC＝∠ABC+∠CAB＝90°，∴∠A＝∠ECB，∵∠BCE＝∠BCD，∴∠A＝∠BCD，∵OC＝OA，∴∠A＝∠ACO，∴∠ACO＝∠BCD，∴∠ACO+∠BCO＝∠BCO+∠BCD＝90°，∴∠DCO＝90°，∴CD是⊙O的切线；（2）解：∵∠A＝∠BCE，∴tanA=BC AC=tan∠BCE=BE CE=12，设BC＝k，AC＝2k，∵∠D＝∠D，∠A＝∠BCD，∴△ACD∽△CBD，∴BC AC=CD AD=12，∵AD＝8，∴CD＝4．17.（2020•衡阳）如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，过点A和点D的圆，圆心O在线段AB上，⊙O交AB于点E，交AC于点F．（1）判断BC与⊙O的位置关系，并说明理由；（2）若AD＝8，AE＝10，求BD的长．【分析】（1）连接OD，根据平行线判定推出OD∥AC，推出OD⊥BC，根据切线的判定推出即可；（2）连接DE，根据圆周角定理得到∠ADE＝90°，根据相似三角形的性质得到AC=325，根据勾股定理得到CD=AD2−AC2==根据相似三角形的性质即可得到结论．【解析】（1）BC与⊙O相切，理由：连接OD，∵OA＝OD，∴∠OAD＝∠ODA，∵AD平分∠BAC，∴∠BAD＝∠CAD，∴∠ODA＝∠CAD，∴OD∥AC，∵∠C＝90°，∴∠ODC＝90°，∴OD⊥BC，∵OD为半径，∴BC是⊙O切线；（2）连接DE，∵AE是⊙O的直径，∴∠ADE＝90°，∵∠C＝90°，∴∠ADE＝∠C，∵∠EAD＝∠DAC，∴△ADE∽△ACD，∴AE AD=AD AC，108=8AC，∴AC=325，∴CD=AD2−AC2==245，∵OD⊥BC，AC⊥BC，∴△OBD∽△ABC，∴OD AC=BD BC，∴5325=BD BD+245，∴BD=1207．18.（2020•遵义）如图，AB是⊙O的直径，点C是⊙O上一点，∠CAB的平分线AD交BC 于点D，过点D作DE∥BC交AC的延长线于点E．（1）求证：DE是⊙O的切线；（2）过点D作DF⊥AB于点F，连接BD．若OF＝1，BF＝2，求BD的长度．【分析】（1）连接OD，由等腰三角形的性质及角平分线的性质得出∠ADO＝∠DAE，从而OD∥AE，由DE∥BC得∠E＝90°，由两直线平行，同旁内角互补得出∠ODE＝90°，由切线的判定定理得出答案；（2）先由直径所对的圆周角是直角得出∠ADB＝90°，再由OF＝1，BF＝2得出OB的值，进而得出AF和BA的值，然后证明△DBF∽△ABD，由相似三角形的性质得比例式，从而求得BD2的值，求算术平方根即可得出BD的值．【解析】（1）连接OD，如图：∵OA＝OD，∴∠OAD＝∠ADO，∵AD平分∠CAB，∴∠DAE＝∠OAD，∴∠ADO＝∠DAE，∴OD∥AE，∵DE∥BC，∴∠E＝90°，∴∠ODE＝180°﹣∠E＝90°，∴DE是⊙O的切线；（2）∵AB是⊙O的直径，∴∠ADB＝90°，∵OF＝1，BF＝2，∴OB＝3，∴AF＝4，BA＝6．∵DF⊥AB，∴∠DFB＝90°，∴∠ADB＝∠DFB，又∵∠DBF＝∠ABD，∴△DBF∽△ABD，∴BD BA=BF BD，∴BD2＝BF•BA＝2×6＝12．∴BD＝23．19.（2019•陕西）如图，⊙O的半径OA＝6，过点A作⊙O的切线AP，且AP＝8，连接PO 并延长，与⊙O交于点B、D，过点B作BC∥OA，并与⊙O交于点C，连接AC、CD．（1）求证：DC∥AP；（2）求AC的长．【分析】（1）根据切线的性质得到∠OAP＝90°，根据圆周角定理得到∠BCD＝90°，根据平行线的性质和判定定理即可得到结论；（2）根据勾股定理和相似三角形的判定和性质定理即可得到结论．【解析】（1）证明：∵AP是⊙O的切线，∴∠OAP＝90°，∵BD是⊙O的直径，∴∠BCD＝90°，∵OA∥CB，∴∠AOP＝∠DBC，∴∠BDC＝∠APO，∴DC∥AP；（2）解：∵AO∥BC，OD＝OB，∴延长AO交DC于点E，则AE⊥DC，OE=12BC，CE=12CD，在Rt△AOP中，OP=62+82=10，由（1）知，△AOP∽△CBD，∴DB OP=BC OA=DC AP，即1210=BC6=DC8，∴BC=365，DC=485，∴OE=185，CE=245，在Rt△AEC中，AC=AE2+CE2==20（2021·云南中考真题）如图，AB 是O 的直径，点C 是O 上异于A 、B 的点，连接AC 、BC ，点D 在BA 的延长线上，且DCA ABC ∠=∠，点E 在DC 的延长线上，且BE DC ⊥．（1）求证：DC 是O 的切线：（2）若2,33OA BE OD ==，求DA 的长．【答案】（1）见解析；（2）910【分析】（1）连接OC ，根据圆周角定理得到∠ACB=90°，根据等量代换得到∠DCO=90°，即可证明DC 是圆O 的切线；（2）根据已知得到OA=2DA ，证明△DCO ∽△DEB ，得到DO CO DB EB =，可得DA=310EB ，即可求出DA 的长．【详解】解：（1）如图，连接OC ，由题意可知：∠ACB 是直径AB 所对的圆周角，∴∠ACB=90°，∵OC ，OB 是圆O 的半径，∴OC=OB ，∴∠OCB=∠ABC ，又∵∠DCA=∠ABC ，∴∠DCA=∠OCB ，∴∠DCO=∠DCA+∠ACO=∠OCB+∠ACO=∠ACB=90°，∴OC ⊥DC ，又∵OC 是圆O 的半径，∴DC 是圆O 的切线；（2）∵23OA OD =，∴23OA OA DA =+，化简得OA=2DA ，由（1）知，∠DCO=90°，∵BE ⊥DC ，即∠DEB=90°，∴∠DCO=∠DEB ，∴OC ∥BE ，∴△DCO ∽△DEB ，∴DO CO DB EB =，即33255DA OA DA DA DA OA OB DA EB+===++，∴DA=310EB ，∵BE=3，∴DA=310EB=3931010⨯=，经检验：DA=910是分式方程的解，∴DA=910．【点睛】本题考查了圆周角定理，相似三角形的判定和性质，切线的判定，正确的作出辅助线，证明切线，得到相似三角形是解题的关键．21.（2021·江苏扬州市·中考真题）如图，四边形ABCD 中，//AD BC ，90BAD ∠=︒，CB CD =，连接BD ，以点B 为圆心，BA 长为半径作B ，交BD 于点E ．（1）试判断CD 与B 的位置关系，并说明理由；（2）若AB =，60BCD ∠=︒，求图中阴影部分的面积．【答案】（1）相切，理由见解析；（2）π-【分析】（1）过点B 作BF ⊥CD ，证明△ABD ≌△FBD ，得到BF=BA ，即可证明CD 与圆B 相切；（2）先证明△BCD 是等边三角形，根据三线合一得到∠ABD=30°，求出AD ，再利用S △ABD -S 扇形ABE 求出阴影部分面积．【详解】解：（1）过点B 作BF ⊥CD ，∵AD ∥BC ，∴∠ADB=∠CBD ，∵CB=CD ，∴∠CBD=∠CDB ，∴∠ADB=∠CDB ，又BD=BD ，∠BAD=∠BFD=90°，∴△ABD ≌△FBD （AAS ），∴BF=BA ，则点F 在圆B 上，∴CD 与圆B 相切；（2）∵∠BCD=60°，CB=CD ，∴△BCD 是等边三角形，∴∠CBD=60°∵BF ⊥CD ，∴∠ABD=∠DBF=∠CBF=30°，∴∠ABF=60°，∵AB=BF=，∴AD=DF=tan30AB ⋅︒=2，∴阴影部分的面积=S △ABD -S 扇形ABE=(230122360π⨯⨯⨯-=π-．【点睛】本题考查了切线的判定，全等三角形的判定和性质，等边三角形的判定和性质，扇形面积，三角函数的定义，题目的综合性较强，难度不小，解题的关键是正确做出辅助线．22.（2020•上海）如图，△ABC中，AB＝AC，⊙O是△ABC的外接圆，BO的延长线交边AC 于点D．（1）求证：∠BAC＝2∠ABD；（2）当△BCD是等腰三角形时，求∠BCD的大小；（3）当AD＝2，CD＝3时，求边BC的长．【分析】（1）连接OA．利用垂径定理以及等腰三角形的性质解决问题即可．（2）分三种情形：①若BD＝CB，则∠C＝∠BDC＝∠ABD+∠BAC＝3∠ABD．②若CD＝CB，则∠CBD＝∠CDB＝3∠ABD．③若DB＝DC，则D与A重合，这种情形不存在．分别利用三角形内角和定理构建方程求解即可．（3）如图3中，作AE∥BC交BD的延长线于E．则AE BC=AD DC=23，推出AO OH=AE BH=43，设OB＝OA＝4a，OH＝3a，根据BH2＝AB2﹣AH2＝OB2﹣OH2，构建方程求出a即可解决问题．【解析】（1）证明：连接OA．A∵AB＝AC，=AC ，∴AB∴OA⊥BC，∴∠BAO＝∠CAO，∵OA＝OB，∴∠ABD＝∠BAO，∴∠BAC＝2∠BAD．（2）解：如图2中，延长AO交BC于H．①若BD＝CB，则∠C＝∠BDC＝∠ABD+∠BAC＝3∠ABD，∵AB＝AC，∴∠ABC＝∠C，∴∠DBC＝2∠ABD，∵∠DBC+∠C+∠BDC＝180°，∴8∠ABD＝180°，∴∠C＝3∠ABD＝67.5°．②若CD＝CB，则∠CBD＝∠CDB＝3∠ABD，∴∠C ＝4∠ABD ，∵∠DBC+∠C+∠CDB ＝180°，∴10∠ABD ＝180°，∴∠BCD ＝4∠ABD ＝72°．③若DB ＝DC ，则D 与A 重合，这种情形不存在．综上所述，∠C 的值为67.5°或72°．（3）如图3中，作AE ∥BC 交BD 的延长线于E ．则AE BC =AD DC =23，∴AO OH =AE BH =43，设OB ＝OA ＝4a ，OH ＝3a ，∵BH 2＝AB 2﹣AH 2＝OB 2﹣OH 2，∴25﹣49a 2＝16a 2﹣9a 2，∴a 2=2556，∴BH =∴BC ＝2BH =23.（2021·云南中考真题）如图，AB 是O 的直径，点C 是O 上异于A 、B 的点，连接AC 、BC ，点D 在BA 的延长线上，且DCA ABC ∠=∠，点E 在DC 的延长线上，且BE DC ⊥．（1）求证：DC是O的切线：（2）若2,33OA BEOD==，求DA的长．【答案】（1）见解析；（2）9 10【分析】（1）连接OC，根据圆周角定理得到∠ACB=90°，根据等量代换得到∠DCO=90°，即可证明DC是圆O的切线；（2）根据已知得到OA=2DA，证明△DCO∽△DEB，得到DO CODB EB=，可得DA=310EB，即可求出DA的长．【详解】解：（1）如图，连接OC，由题意可知：∠ACB是直径AB所对的圆周角，∴∠ACB=90°，∵OC，OB是圆O的半径，∴OC=OB，∴∠OCB=∠ABC，又∵∠DCA=∠ABC，∴∠DCA=∠OCB，∴∠DCO=∠DCA+∠ACO=∠OCB+∠ACO=∠ACB=90°，∴OC⊥DC，又∵OC 是圆O 的半径，∴DC 是圆O 的切线；（2）∵23OA OD =，∴23OA OA DA =+，化简得OA=2DA ，由（1）知，∠DCO=90°，∵BE ⊥DC ，即∠DEB=90°，∴∠DCO=∠DEB ，∴OC ∥BE ，∴△DCO ∽△DEB ，∴DO CO DB EB =，即33255DA OA DA DA DA OA OB DA EB +===++，∴DA=310EB ，∵BE=3，∴DA=310EB=3931010⨯=，经检验：DA=910是分式方程的解，∴DA=910．【点睛】本题考查了圆周角定理，相似三角形的判定和性质，切线的判定，正确的作出辅助线，证明切线，得到相似三角形是解题的关键．类型三与锐角三角函数有关24.(2022·辽宁省铁岭市)如图，△ABC内接于⊙O，AC是⊙O的直径，过OA上的点P作PD⊥AC，交CB的延长线于点D，交AB于点E，点F为DE的中点，连接BF．(1)求证：BF与⊙O相切；(2)若AP=OP，cosA=45，AP=4，求BF的长．【答案】(1)连接OB，根据直径所对的圆周角是直角可得∠ABC=90°，从而可得∠ABD=90°，进而利用直角三角形三角形斜边上的中线可得BF=EF=12AD，然后利用等腰三角形的性质可得∠FEB=∠FBE，从而可得∠FBE=∠AEP，最后根据垂直定义可得∠EPA=90°，从而可得∠A+∠AEP=90°，再利用等腰三角形的性质可得∠A=∠OBA，从而可得∠OBA+∠FBE= 90°，进而可得∠OBF=90°，即可解答；(2)在Rt△AEP中，利用锐角三角函数的定义求出AE的长，从而利用勾股定理求出PE的长，然后利用同角的余角相等可得∠AEP=∠C，从而可证△APE∽△DPC，进而利用相似三角形的性质可求出DP的长，最后求出DE的长，即可解答．本题考查了解直角三角形，切线的判定与性质，圆周角定理，三角形的外接圆与外心，直线与圆的位置关系，熟练掌握解直角三角形，以及切线的判定与性质是解题的关键．25.(2022·四川省广安市)如图，AB为⊙O的直径，D、E是⊙O上的两点，延长AB至点C，连接CD ，∠BDC =∠BAD ．(1)求证：CD 是⊙O 的切线．(2)若tan∠BED =23，AC =9，求⊙O 的半径．【答案】（1）连接OD ，由圆周角定理得出∠ADB =90°，证出OD ⊥CD ，由切线的判定可得出结论；(2)证明△BDC∽△DAC ，由相似三角形的性质得出CD AC =BC CD =BD DA =23，由比例线段求出CD 和BC 的长，可求出AB 的长，则可得出答案．本题考查了切线的判定，相似三角形的判定与性质，锐角三角函数的定义，圆周角定理，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．26.（2021·山东菏泽市·中考真题）如图，在O 中，AB 是直径，弦CD AB ⊥，垂足为H ，E 为 BC上一点，F 为弦DC 延长线上一点，连接FE 并延长交直径AB 的延长线于点G ，连接AE 交CD 于点P ，若FE FP =．（1）求证：FE 是O 的切线；（2）若O 的半径为8，3sin 5F =，求BG 的长．【答案】（1）见解析；（2）=2BG 【分析】（1）连接OE ，证明OE ⊥EF 即可；（2）由3sin 5F =证得4sin 5G =，运用正弦的概念可得结论．【详解】解：（1）证明：连接OE ，如图，∵OA=OE∴∠OAE=∠OEA ．∵EF=PF ，∴∠EPF=∠PEF∵∠APH=∠EPF ，∴∠APH=∠EPF ，∴∠AEF=∠APH ．∵CD ⊥AB ，∴∠AHC=90°．∴∠OAE+∠APH=90°．∴∠OEA+∠AEF=90°∴∠OEF=90°∴OE ⊥EF ．∵OE 是O 的半径∴EF 是圆的切线，（2）∵CD ⊥AB∴FHG ∆是直角三角形∵3sin 5F =∴35GH FG =设3GH x =，则5FG x=由勾股定理得，4FH x=由（1）得，OEG ∆是直角三角形∴4sin 5OE FH x G OG FG x===∴45OE OG =，即45OE OE BG =+∵8OE =∴8485BG =+解得，2BG =【点睛】此题主要考查了圆的切线的判定，勾股定理和解直角三角形等知识，熟练掌握切线的判定是解答此题的关键．27.（2022·黔东南）（1）请在图中作出△ABC 的外接圆⊙O （尺规作图，保留作图痕迹，不写作法）；的中点，过点B的（2）如图，⊙O是△ABC的外接圆，AE是⊙O的直径，点B是CE切线与AC的延长线交于点D.①求证：BD⊥AD；②若AC=6，tan∠ABC=34，求⊙O的半径.【答案】（1）解：如下图所示（2）解：①如下图所示，连接OC、OB∵BD是⊙O的切线∴OB⊥BD对应的圆周角，∠COE是CE 对应的圆心角∵∠CAE是CE∴∠COE=2∠CAE的中点∵点B是CE∴∠COE=2∠BOE∴∠CAE=∠BOE∴∠CAE=∠BOE∴AD//OB∴BD⊥AD②如下图所示，连接CE对应的圆周角∵∠ABC与∠AEC是AC∴∠ABC=∠AEC∵AE是⊙O的直径∴∠ACE=90°∴tan∠AEC=AC CE=34∴CE=8∵AE2=CE2+AC2∴AE=10∴⊙O的半径为5.【知识点】圆周角定理；三角形的外接圆与外心；切线的性质；解直角三角形；作图-线段垂直平分线【解析】【解答】（1）∵△ABC的外接圆⊙O的圆心为任意两边的垂直平分线的交点，半径为交点到任意顶点的距离，∴做AB、AC的垂直平分线交于点O，以OB为半径，以O为圆心做圆即可得到△ABC 的外接圆；【分析】（1）利用尺规作图分别作出AC，AB的垂直平分线，两垂直平分线交于点O，然后以点O为圆心，OB的长为半径画圆即可.（2）①连接OC，OB，利用切线的性质可证得OB⊥BD，利用圆周角定理可证得∠COE=2∠CAE，由点B是弧CE的中点，可推出∠CAE=∠BOE，利用平行线的判定定理可证得AD∥OB，由此可证得结论；②连接CE，利用同弧所对的圆周角相等，可证得∠ABC=∠AEC，利用直径所对的圆周角是直角，可推出∠ACE=90°；再利用解直角三角形求出CE的长，利用勾股定理求出AE的长.28.（2022·鄂州）如图，△ABC内接于⊙O，P是⊙O的直径AB延长线上一点，∠PCB=∠OAC，过点O作BC的平行线交PC的延长线于点D.（1）试判断PC与⊙O的位置关系，并说明理由；（2）若PC＝4，tanA＝12，求△OCD的面积.【答案】（1）解：PC与⊙O相切，理由如下：∵AB是圆O的直径，∴∠ACB=90°，∴∠OCB+∠OCA=90°，∵OA=OC，∴∠OCA=∠OAC，∵∠PCB=∠OAC，∴∠PCB=∠OCA，∴∠PCB+∠OCB=∠OCA+∠OCB=90°，即∠PCO=90°，∴PC与⊙O相切（2）解：∵∠ACB=90°，tanA=12，∴BC AC=12，∵∠PCB=∠OAC，∠P=∠P，∴△PBC∽△PCA，∴PC PA=PB PC=BC CA=12，∴PA=8，PB=2，∴AB=6，∴OC=OB=3，∴OP=5，∵BC∥OD，∴△PBC∽△POD，∴PB OP=PC PD，即25=4PD，∴PD=10，∴CD=6，∴S△OCD=12OC⋅CD=9【知识点】等腰三角形的性质；圆周角定理；切线的判定；相似三角形的判定与性质；锐角三角函数的定义【解析】【分析】（1）由圆周角定理得∠ACB=90°，根据等腰三角形的性质可得∠OCA=∠OAC，结合∠PCB=∠OAC得PCB=∠OCA，结合∠OCB+∠OCA=90°可得∠PCO=90°，据此证明；（2）根据三角函数的概念可得BC AC=12，易证△PBC∽△PCA，根据相似三角形的性质可得PA、PB，然后求出AB、OP，证明△PBC∽△POD，根据相似三角形的性质可得PD，由PD-PC=CD可得CD，然后根据三角形的面积公式进行计算.29.（2022·毕节）如图，在△ABC中，∠ACB=90∘，D是AB边上一点，以BD为直径的⊙O与AC相切于点E，连接DE并延长交BC的延长线于点F.（1）求证：BF=BD；（2）若CF=1，tan∠EDB=2，求⊙O直径.【答案】（1）证明：连接OE，如下图所示：∵AC为圆O的切线，∴∠AEO=90°，∵AC⊥BC，∴∠ACB=90°，∴OE∥BC，∴∠F=∠DEO，又∵OD=OE，∴∠ODE=∠DEO，∴∠F=∠ODE，∴BD=BF.（2）解：连接BE，如下图所示：由(1)中证明过程可知：∠EDB=∠F，。
中考复习专题-圆切线证明
例3如图，AB是€）0的直径，弦AC与AB成30°角，CD与OO切于C,交AB的延长线于D,求证:
AC二CD・
例4如图20-12, BC为OO的直径，ADI BC,垂足为D,AB = AF,BF和AD交于巳
求证：AE二BE・
⑴ 求证：AD二DC・（2）求证：DE是OO】的切线.
点E, OE交AD于点F.⑴求证：DE是OO的切线；⑵若—求寺的值。
AB5DF
3如图，Rt/\ABC中，ZABC = 90\以A3为直径作OO交AC边于点D,E是边3C的中点，连接£>£・
(1) 求证：直线QE是<90的切线；
(2)连接OC交DE于点F,若OF = CF,求tanZACO的值.
4.如图，点O在ZAPB的平分线上，C, BD与0O切于A、B,且AC//BD,若上COD二90°.求证：CD是OO的切线.
［习题练习］
例1如图，AB是OO的弦（非直径），C、D是AB上两点，并旦OC二OD,求证：AC二BD.
例2已知：如图，在AABC中，AB二AC,以AB为直径的OO与BC交于点D,与AC交于点巳求证:
B
例6如图，已知直线MN与以AB为直径的半圆相切于点C,上A二28°・
(1)求ZACM的度数.(2)在MN上是否存在一点D,使AB • CD二AC • BC,说明理由.
例7如图，在RtAABC中，上090° ,AC二5,BC二12,OO的半径为3.
(1)若圆心o与c重合时，OO与AB有怎样的位萱关系？
(1)求ZPOQ;
(2)设D是CA延长线上的一个动点，DE与OO相切于点M,点E在CB的延长线上，试判断ZDOE的大小是否保持不变，并说明理由。
1如图，等腰三角形S3O中，/4C=BC=10,AB=I2。以30为直径作OO交/4B于点。交SU于点G, DFLAC,垂足为斤交6的延长线于点仁
圆的切线证明题
CEABOP细说如何证明圆的切线1、证切线---------------90°〔垂直〕2、有90°------------------证全等3、有⊥------------------证∥，错过来4、利用角+角=90°关注：等腰〔等边〕三线合一；中位线；直角三角形1〔2021中考〕.如图，PA为⊙O的切线，A为切点，过A作OP的垂线AB，垂足为点C,交⊙O于点B,延长BO与⊙O交于点D，与PA的延长线交于点E,(1)求证：PB为⊙O的切线；2 ⊙O中，AB是直径，过B点作⊙O的切线，连结CO，假设AD∥OC交⊙O于D，求证：CD是⊙O 的切线。
3 如图，AB=AC，AB是⊙O的直径，⊙O交BC于D，DM⊥AC于M求证：DM与⊙O相切.D4(2021年厦门市)：如图，中，，以为直径的交于点，于点．〔1〕求证：是的切线；5：如图⊙O是△ABC的外接圆，P为圆外一点，PA∥BC，且A为劣弧的中点，割线PBD过圆心，交⊙0于另一点D，连结CD．(1)试判断直线PA与⊙0的位置关系，并证明你的结论．(2)当AB=13，BC=24时，求⊙O的半径及CD的长．6如图，点B、C、D都在半径为6的⊙O上，过点C作AC∥BD交OB的延长线于点A，连接CD，∠CDB=∠OBD=30°．(1)求证：AC是⊙O的切线；(2)求弦BD的长；(3)求图中阴影局部的面积．7.〔2021北京中考〕：如图，在△ABC中，D是AB边上一点，圆O过D、B、C三点，∠DOC=2∠ACD=90︒。
(1) 求证：直线AC是圆O的切线；(2) 如果∠ACB=75︒，圆O的半径为2，求BD的长。
8、〔2021•北京〕如图，在△ABC，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F 在AC的延长线上，且∠CBF=∠CAB．〔1〕求证：直线BF是⊙O的切线；9 ⊙O的半径OA⊥OB，点P在OB的延长线上，连结AP交⊙O于D，过D作⊙O的切线CE交OP 于C，求证：PC＝CD。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
圆切线证明题
1.如图，PA为O O的切线，A为切点，过A作OP的垂线AB,垂足为点C,交O O于点B,延长B0与O O交于点D,与PA的延长线交于点E,
求证：PB为O 0的切线;
2如图，AB=AC AB是O 0的直径，O O交BC于D, DML AC于M
求证：DM与O O相切.
3如图，已知：AB是O 0的直径，点C在O O上，且/ CAB=30, BD=OB D在AB的延长线上
求证：DC是O 0的切线
3.已知：如图，A是LI 0上一点，半径0C的延长线与过点A的直线交于B点，OC=BC ,
1
AC OB •
2
(1)求证：AB是L O的切线；一一
(2 )若丄ACD=45°OC=2，求弦CD 的长. / \
4.知：如图，在Rt A ABC中，• C=90〃，点O在AB上，以O为圆心，OA长为半径的
圆与AC, AB 分别交于点D, E ，且.CBD A .
(1 )判断直线BD 与LI O 的位置关系，并证明你的结论; 已知：如图，在 △ ABC 中, D 是AB 边上一点，圆 0过D B C 三点，.DOC2. ACD 90。
(1) 求证：直线AC 是圆0的切线；
,如图，AB=AC D 为BC 中点，O D 与AB 切于E 点.
求证：AC 与O D 相切.
如图，等腰三角形 ABC 中，AC= BC= 10，AB= 12。
以BC 为直径作O O 交AB 于点D,交AC
C
B
于点G DF 丄AC 垂足为F ,交CB 的延长线于点 E 。
⑴求证：直线EF 是O O 的切线；
如图，Rt △ ABC 中，N ABC = 90°以AB 为直径作O O 交AC 边于点D ，E 是边BC
的中点，连接DE .
(1)求证：直线DE 是O O 的切线;
如图，点 O 在/ APB 的平分线上，O O 与PA 相切于点 C.
(1) 求证：直线 PB 与O O 相切;
23.(2008年南充市)如图，已知］的直径』垂直于弦二 于点二，过」点作’ 交；的延长线于点 」，连接并延长交J U 于点；，且_［「__［」
.
E
B
(1) 试问: 丄是― 的切线吗？说明理由;
(2) 请证明是］］的中点；
(3) 若； — ，求二.的长.
24.(本题8分)如图，已知 CD >^ ABC 中 AB 边上的高，以 CD 为直径的O O 分别交CA CB 于点E 、F ,点G 是AD 的中点.求证：GE 是O O 的切线.
25. (2008年龙岩市)(13分)如图，在平面直角坐标系 xOy 中，O 0交x 轴于A 、B 两点， 直线FA! x 轴于点A 点D 在FA 上,且DO 平行O 0的弦MB 连DM 并延长交x 轴于点C.
(1 )判断直线 DC 与O 0的位置关系，并给出证明；
(2)设点D 的坐标为(-2 , 4),试求MC 的长及直线DC 的解析式.
10.如图，在厶ABC 中，AB=AC,以AB 为直径作 O 0交BC 于点D,过点D 作DEL AC 于E.判断 DE 与O O 的位置
关系，并证明.
27.(本题满分10分)如图，四边形 ABCD 内接于O O, BD 是O O O
的直径，AE _ CD ，垂足为E , DA 平分
(1) 求证：AE 是O O 的切线；
(2) 若• DBC =30：, DE -1cm ，求 BD 的长.
A B
D C
E
欢迎您的下载，
资料仅供参考!
致力为企业和个人提供合同协议，策划案计划书，学习资料等等
打造全网一站式需求。