高一数学对数与对数运算2
高一数学上册 第二章基本初等函数之对数函数知识点总结及练习题(含答案)

〖2.2〗对数函数【2.2.1】对数与对数运算(1)对数的定义①若 , 则 叫做以 为底 的对数, 记作 , 其中 叫做底数, 叫做真数. ②负数和零没有对数. ③对数式与指数式的互化: .(2)几个重要的对数恒等式: , , .(3)常用对数与自然对数:常用对数: , 即 ;自然对数: , 即 (其中 …). (4)对数的运算性质 如果 , 那么 ①加法: ②减法: ③数乘:④log a N a N = ⑤log log (0,)bn a a nM M b n R b=≠∈ ⑥换底公式:【2.2.2】对数函数及其性质(5)对数函数(6)反函数的概念设函数 的定义域为 , 值域为 , 从式子 中解出 , 得式子 . 如果对于 在 中的任何一个值, 通过式子 , 在 中都有唯一确定的值和它对应, 那么式子 表示 是 的函数, 函数 叫做函数 的反函数, 记作 , 习惯上改写成 .(7)反函数的求法①确定反函数的定义域, 即原函数的值域;②从原函数式 中反解出 ; ③将 改写成 , 并注明反函数的定义域. (8)反函数的性质①原函数 与反函数 的图象关于直线 对称.②函数 的定义域、值域分别是其反函数 的值域、定义域. ③若 在原函数 的图象上, 则 在反函数 的图象上. ④一般地, 函数 要有反函数则它必须为单调函数.一、选择题:1. 的值是( )A.B. 1C. D. 22. 已知x= +1,则log4(x3-x -6)等于 ( ) A.23 B.45 C.0 D.21 3. 已知lg2=a, lg3=b, 则 等于 ( ) A.B.C. D. 4.已知2lg(x -2y)=lgx +lgy, 则 的值为( )A. 1B. 4C. 1或4D. 4或-15.函数y=)12(log 21 x 的定义域为( ) A. ( , +∞) B. [1, +∞ C. ( , 1 D. (-∞, 1) 6.已知f(ex)=x, 则f(5)等于 ( )A. e5B. 5eC. ln5D. log5e7. 若 的图像是 ( )A B C D8. 设集合等于()A. B.C. D.9. 函数的反函数为()A. B.C. D.二、填空题:10. 计算: log2.56.25+lg +ln +=11. 函数y=log4(x-1)2(x<1的反函数为__________ .12. 函数y=(log x)2-log x2+5在2≤x≤4时的值域为______.三、解答题:13.已知y=loga(2-ax)在区间{0, 1}上是x的减函数, 求a的取值范围.14. 已知函数f(x)=lg[(a2-1) x2+(a+1)x+1], 若f(x)的定义域为R, 求实数a的取值范围.15. 已知f(x)=x2+(lga+2)x+lgb, f(-1)=-2, 当x∈R时f(x)≥2x恒成立, 求实数a的值, 并求此时f(x)的最小值?一、选择题: ABBCBCDCBAAB13. , 14.y=1-2x(x∈R), 15.(lgm)0.9≤(lgm)0.8, 16.17.解析: 因为a是底, 所以其必须满足a>0 且a不等于1a>0所以2-ax为减函数, 要是Y=loga(2-ax)为减函数, 则Y=loga(Z)为增函数, 得a>1又知减函数区间为[0,1], a必须满足2-a*0>0 2-a*1>0 即得a<2综上所述, 啊的取值范围是(1,2)18、解: 依题意(a2-1)x2+(a+1)x+1>0对一切x∈R恒成立.当a2-1≠0时, 其充要条件是: 解得a<-1或a>又a=-1, f(x)=0满足题意, a=1, 不合题意.所以a的取值范围是: (-∞, -1]∪( , +∞)19、解析:由f(-1)=-2, 得:f(-1)=1-(lga+2)+lgb=-2, 解之lga-lgb=1,∴=10, a=10b.又由x∈R, f(x)≥2x恒成立.知:x2+(lga+2)x+lgb≥2x, 即x2+xlga+lgb≥0, 对x∈R恒成立, 由Δ=lg2a-4lgb≤0, 整理得(1+lgb)2-4lgb≤0即(lgb-1)2≤0, 只有lgb=1, 不等式成立.即b=10, ∴a=100.∴f(x)=x2+4x+1=(2+x)2-3当x=-2时, f(x)min=-3.。
高一数学对数与对数运算2(新编201910)

4.指数运算法则
4.指数运算法则
a m a n a mn (m, n R), (am )n amn (m, n R), (ab)n a n bn (n R).
讲授新课
1.积、商、幂的对数运算法则:
讲授新课
1.积、商、幂的对数运算法则:
如果a>0,且a≠1,M>0,N>0有:
讲授新课
1.积、商、幂的对数运算法则:
如果a>0,且a≠1,M>0,N>0有:
loga (MN ) loga M loga N (1)
讲授新课
1.积、商、幂的对数运算法则:
如果a>0,且a≠1,M>0,N>0有:
loga (MN ) loga M loga N (1)
log aM Nຫໍສະໝຸດ log aM
loga
N
(2)
讲授新课
1.积、商、幂的对数运算法则:
如果a>0,且a≠1,M>0,N>0有:
loga (MN ) loga M loga N (1)
log a
M N
log a
M
loga
N
(2)
log a M n n log a M (n R) (3)
说 明: ①简易语言表达:
“积的对数=对数的和”……
说 明: ①简易语言表达:
“积的对数=对数的和”……
②有时逆向运用公式:
如:log10 5 log10 2 log10 10 1.
说 明: ①简易语言表达:
2.指数式与对数式的互化
2.指数式与对数式的互化
ab N loga N b (a 0且a 1)
2.指数式与对数式的互化
高一数学对数的概念及运算2

高中数学 2.2.2对数与对数运算(二)练习 新人教A版必修1-新人教A版高一必修1数学试题

【金版学案】2015-2016高中数学 对数与对数运算(二)练习 新人教A 版必修1 基础梳理1.设a >0,a ≠1,M >0,N >0,则有(1)log a (MN )=log a M +log a N ,简记为:积的对数=对数的和.(2)log a MN=log a M -log a N ,简记为:商的对数=对数的差.(3)log a M n =n log a M (n ∈R). 例如:①lg (3×5)=______;②lg 5+lg 2=______;③ln e 2=______.2.几点注意:(1)对数的真数是多项式时,需将真数部分加括号,如lg(x +y )与lg x +y 的含义不同.(2)(lg M )n 与lg M n 的含义不同.(3)log 2(-3)(-5)=log 2(-3)+log 2(-5)是不成立的.(4)log 10(-10)2=2log 10(-10)是不成立的.(5)当心记忆错误:log a (MN )≠log a M ·log a N ;log a (M ±N )≠log a M ±log a N .3.对数的换底公式log a b =log c b log c a(a >0,且a ≠1;c >0,且c ≠1;b >0).换底公式的意义是把一个对数式的底数改变,可将不同底问题化为同底,便于使用运算法则.例如:log 35=________,其中a >0,且a ≠1.4.关于对数换底公式的证明方法有很多,可借助指数式证明对数换底公式.例如:设a >0,且a ≠1;c >0,且c ≠1;b >0.求证:log a b =log c b log c a.5.设a ,b >0,且均不为1,由换底公式可加以求证:(1)log a b ·log b a =1;(2)log am b n =n mlog a b .例如:①log 23·log 32=____;②log 89=________ .基础梳理1.①lg 3+lg 5 ②1 ③2 3.log a 5log a 34.证明:设log a b =x ,则b =a x ,于是log c b =log c a x ,即x log c a =log c b ,∴x =log c b log c a ,∴log a b =log c b log c a. 5.证明:(1)log a b ·log b a =lg b lg a ·lg a lg b=1. (2)log am b n =lg b n lg a m =n lg b m lg a =n mlog a b . 答案:1 23log 23 ,思考应用1.log a (M +N )=log a (MN )对吗?1.错2.log a (M -N )=log a M N 对吗?2错 自测自评1.若a >0,a ≠1,x >y >0,下列式子:①log a x ·log a y =log a (x +y );②log a x -log a y =log a (x -y );③log a xy=log a x ÷log a y ;④log a (xy )=log a x ·log a y .其中正确的个数为( ) A .0个 B .1个C .2个D .3个2.设9a =45,log 95=b ,则( )A .a =b +9B .a -b =1C .a =9bD .a ÷b =13.求值:log 274log 32=____. 1.解析:根据对数的性质知4个式子均不正确.故选A.答案:A2.解析:由9a =45得a =log 945=log 99+log 95=1+b ,即a -b =1,故选B. 答案:B3.解析:log 274log 32=lg 4lg 27lg 2lg 3=2lg 23lg 3lg 2lg 3=23. 答案:23►基础达标1.lg a 与lg b 互为相反数,则( )A .a +b =0B .a -b =0C .ab =1 D.a b=11.C2.在log (a -2)2中,a 的取值X 围是____________.2.(2,3)∪(3,+∞)3.已知log 5[log 4(log 3x )]=0,则x =____.3.814.化简12log 612-2log 62的结果为( ) A .6 2 B .12 2C .log 6 3 D.124.解析:12log 612-2log 62=12(1+log 62)-log 62=12(1-log 62)=12log 63=log 6 3.故选C.答案:C5.(log 29)·(log 34)=( )A.14B.12C .2D .4 5.解析:原式=lg 9lg 2·lg 4lg 3=2lg 3·2lg 2lg 2·lg 3=4. 答案:D6.设lg 2=a ,lg 3=b ,则log 512等于( )A.2a +b 1+aB.a +2b 1+aC.2a +b 1-aD.a +2b 1-a6.解析:log 512=lg 12lg 5=lg 3+2lg 2lg 5=lg 3+2lg 21-lg 2= b +2a 1-a. 答案:C►巩固提高7.(lg 2)3+(lg 5)3+3lg 2 lg 5的值是( )A .4B .1C .6D .37.B8.(2014·某某卷)已知a =2-13,b =log 2,c =log 1213,则( ) A .a >b >c B .a >c >bC .c >a >bD .c >b >a8.解析:0<a =2-13<20=1,b =log 213<0,a =log 1213=log 23>1,所以c >a >b ,故选C.答案:C9.求值:(lg 2)2+lg 2·lg 50+lg 25.9.解析:(lg 2)2+lg 2·lg 50+lg 25=lg 2(lg 2+lg 50)+lg 25=2lg 2+lg 25=lg 100=2.10.求值:(log 32+log 92)·(log 43+log 83).10.解析:(log 32+log 92)·(log 43+log 83)=⎝⎛⎭⎪⎫log 32+log 32log 39·⎝ ⎛⎭⎪⎫log 33log 34+log 33log 38 =32log 32·⎝ ⎛⎭⎪⎫12log 32+13log 32 =34+12=54.1.条件代数式的求值问题包括以下三个方面:①若条件简单,结论复杂,可从化简结论入手;②若条件复杂,结论简单,可从化简条件入手,转化成结论的形式;③若条件与结论的复杂程度相差无几时,可同时对它们进行化简,直到找出它们之间的联系为止.2.利用换底公式统一对数的底数,即化异为同是处理含不同底的对数的常用方法.3.在化简、求值、证明等问题中,要把换底公式与对数的运算性质结合起来.4.有时需将对数式log a 5log a 3写成log 35后解决有关问题.。
2023-2024学年高一上数学必修一:对数的运算(2)

11.若 lgx-lgy=a,则 lgx23-lgy23= 3a .(用含有 a 的式子表示) 解析:∵lgx-lgy=a,∴lgxy=a,∴lgx23-lgy23=lg22yx33=lgxy3 =3lgxy=3a.
6.若 log2x·log34·log59=8,则 x 等于( B ) A.8 B.25 C.16 D.4
解析:∵log2x·log34·log59=llgg2x ×llgg43×llgg95=llgg2x ×2llgg32×2llgg53 =8, ∴lgx=2lg5,∴x=25.
7.已知 ab>0,给出下面四个等式: ①lg(ab)=lga+lgb;②lgab=lga-lgb; ③12lgab2=lgab;④lg(ab)=log1ab10. 其中正确的个数为( B ) A.0 B.1 C.2 D.3 解析:当 a<0,b<0 时,lg(ab)=lg(-a)+lg(-b),lgab=lg(-a)-lg(- b),故①②错误;当 ab>0 时,ab>0,12lg(ab)2=lgab,③正确;当 ab=1 时,④错误.因此只有一个正确,故选 B.
三、解答题(共 20 分) 12.(10 分)计算下列各式的值: (1)2lg5+lg4+eln2+log 22 2;
(2)log2 478+log212-12log242+12log23; (3)(log23+log89)(log34+log98+log32).
13.(10 分)候鸟每年都要随季节的变化而进行大规模迁徙,研究某 种候鸟的专家发现,该种候鸟的飞行速度 v(单位:m·s-1)与其耗氧量 Q 之间的关系为 v=a+blog31Q0(其中 a,b 是常数).据统计,该种鸟类在 静止时的耗氧量为 30 个单位,而其耗氧量为 90 个单位时,飞行速度为 1 m·s-1.若这种候鸟为赶路程,飞行的速度不能低于 2 m·s-1,求其耗氧 量至少要多少个单位.
4.3.2对数的运算课件(换底公式)-高一上学期数学人教A版(2019)必修第一册

n
N log a N
m
n
特别地:当m=1时,
log a M nlog a M
n
(n∈R)即公式(3)
其他重要公式3:
log a b
1
log b a
a, b (0,1) (1,)
证明:由换底公式 loga b logb a
lg b lg a
1
lg a lg b
即
1
log a b
1
2
∴
1
2
log36 36 =2log 363=log36 9,
log363
1
log 3636 =log 364.
log36 4
=log 369+log 364=log 3636=1.
板书设计
Байду номын сангаас对数与对数运算:换底公式
logc N
loga N
logc a
log a m
(a, c (0,1) (1,), N 0)
对数函数
——对数与对数运算(2)
学习目标(1分钟)
1、熟练地运用对数运算性质解决问题
2、掌握对数的换底公式,并能正确应用
问题导学(8分钟)
根据P125-126页,探究:
(1)计算log24和log216值;
(2)根据对数的定义,你能利用log24,log216的值求
log416 的值吗?
(3)换底公式的定义是?由换底公式能推导出哪些重
p
log c N log c a , log c N p log c a,
p
log c N
log
N
c
高一数学对数的概念及运算2

3) lg 2 lg 5
4)
log3
27 5
log3
2 3
log3
6 5
5) log2
7 48
log2 12
1 2
log 2
42
1
6)(lg 2)2 lg 2 lg 50 lg 25
例3:已知 loga 18 m, loga 24 n ,求loga 24 n ?
拓展
科学家以里氏震级来度量地震的强度,若设I为地
↓a↓b =↓N log↓a ↓ N=↓b
底数 指数 幂
底数 真数 对数
证明:②设 loga M p, loga N q,
由对数的定义可以得:M a p , N aq
∴ M ap N aq
a pq
loga
M N
pq
即证得
log a
M N
log a M
logaN
(2)
↓a↓b =↓N log↓a ↓ N=↓b
(a m )n a mn (m, n R)
(ab)n a n b n (n R)
证明:①设 loga M p, loga N q,
由对数的定义可以得:M a p , N aq ∴MN= a p aq a pq loga MN p q
即证得
loga (MN) logaM logaN (1)
对数的运算
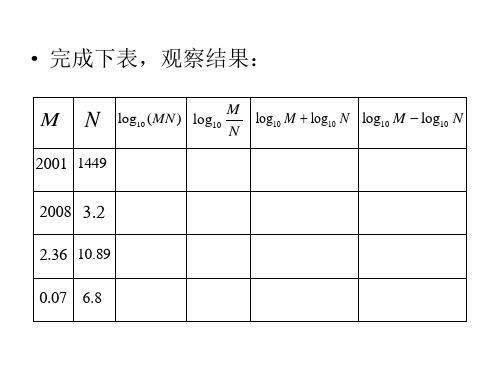
• 完成下表,观察结果:
M
N log10 (MN )
log10
M N
log10 M log10 N log10 M log10 N
2001 1449
2008 3.2
2.36 10.89 0.07 6.8
• 猜测:
loga (MN ) loga M loga N
高一数学对数的概念及运算2(PPT)3-3
积、商、幂的对数运算法则:
如果 a > 0,a 1,M > 0, N > 0 有:
loga (MN) loga M loga N (1)
loga
M N
loga M
Hale Waihona Puke loga N(2)
loga Mn nloga M(n R) (3)
为了证明以上公式,请同学们 回顾一下指数运算法则 :
a m a n a mn (m, n R)
(a m )n a mn (m, n R)
(ab)n a n bn (n R)
• 完成下表,观察结果:
M
N log10 (MN )
log10
M N
log10 M log10 N log10 M log10 N
2001 1449
2008 3.2
2.36 10.89 0.07 6.8
或者吃发绿的马铃薯。致死的事件也不是突发的,当事人在食用后往往是起初虚弱无力,而后陷入昏迷。不用担心偶尔吃到的绿色马铃薯片,但一定要把长 了绿芽或表皮变绿了的马铃薯扔掉,不要再去烧煮食用,特别要小心别给儿童吃。 [] 马铃薯含有一些有毒的生物碱,主要是茄碱和毛壳霉碱,但一般经过℃ 的高温烹调,有毒物质;炒股入门 炒股入门 ; 就会分解。野生的马铃薯毒性较高,茄碱中毒会导致头痛、腹泻、抽搐,昏迷,甚至会导致死亡。 但一般栽培的马铃薯毒性很低,很少有马铃薯中毒事件发生。栽培马铃薯一般含生物碱低于.毫克/克,一般超过毫克才会导致中毒现象,相当于一次吃掉.公 斤生马铃薯。马铃薯储存时如果暴露在光线下,会变绿,同时有毒物质会增加;发芽马铃薯芽眼部分变紫也会使有毒物质积累,容易发生中毒事件,食用时 要特别注意。 [] 马铃薯(土豆)发芽后可产生较高的有毒生物碱——龙葵素(Solanine),食后可引起中毒。马铃薯中龙葵素的一般含量为~mg/g,如发芽、 皮变绿后可达~mg/g,能引起中毒。龙葵素在幼芽及芽其部的含量最多。当食入.~.g龙葵素时,就能发生严重中毒。 [] 孕妇经常食用生物碱含量较高的薯 类,蓄积在体内就可能导致胎儿畸形。当然,人的个体差异相当大,并非每个人食用了薯类都会发生异常,但是孕妇还是以不吃或少吃薯类为好,特别是不 吃长期贮存、发芽的薯类,这一点对处于妊娠早期的妇女来说尤其重要。 [] 中毒原因 引起发芽马铃薯中毒的主要原因是由于马铃薯贮藏不当,使其发芽或 部分变黑绿色,烹调时又未能除去或破坏龙葵素,食后便发生中毒。 [] 中毒症状 症状因服用量的多少表现轻重不一。主要表现如下,食后几小时内发病。 口腔内有烧灼和痒感、畏光、头痛、头晕、发热、呕吐、腹痛、腹泻、耳鸣等,进一步加重可能出现血压下降、烦躁不安、抽搐、呼吸困难、昏迷、瞳孔散 大等。 [] 急救措施 ①用筷子等刺激咽部催吐。多饮白水或糖水。 [] ②可服浓茶或喝些醋以分解龙葵素。 [] ③口服诸如:硫酸钠、硫酸镁等泻导泻。 [] ④ 病情严重者,急送医院。 [] 预防措施 ①不吃未成熟的青皮马铃薯。对于马铃薯上已经出现发芽、发青的部位或腐烂的部分要彻底清除。如果马铃薯的发青 面积较大,发芽部位也很多,就不能够再食用了。 [] ②去皮后的马铃薯要切成块、片或丝,放在冷水中浸泡,要泡半小时以上,能够使残存的茄碱充分溶解
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
