列举构造等腰三角形4种常用方法模型
构造等腰三角形解题的常见途径

构造等腰三角形解题的常见途径等腰三角形是研究几何图形的基础,因此在许多几何问题中,常常需要构造等腰三角形才能使问题获解,那么如何构造等腰三角形呢?一般说来有以下几种途径:一、利用角平分线+平行线,构造等腰三角形当一个三角形中出现角平分线和平行线时,我们就可以寻找到等腰三角形.如图1①中,若AD 平分∠BAC ,AD ∥EC ,则△ACE 是等腰三角形;如图1②中,AD 平分∠BAC ,DE ∥AC ,则△ADE 是等腰三角形;如图1③中,AD 平分∠BAC ,CE ∥AB ,则△ACE 是等腰三角形;如图1④中,AD 平分∠BAC ,EF ∥AD ,则△AGE 是等腰三角形.例1 如图2,△ABC 中,AB =AC ,在AC 上取点P ,过点P 作EF ⊥BC ,交BA 的延长线于点E ,垂足为点F .求证:.AE =AP .简析 要证.AE =AP ,可寻找一条角平分线与EF 平行,于是想到AB =AC ,则可以作AD 平分∠BAC ,所以AD ⊥BC ,而EF ⊥BC ,所以AD ∥EF ,所以可得到△AEP 是等腰三角形,故AE =AP .例2 如图3,在△ABC 中,∠BAC 、∠BCA 的平分线相交于点O ,过点O 作DE ∥CABE DO图3图4F CDEBA M图2 FB ACD P E图1①D ②C D C ④FCDAC ,分别交AB 、BC 于点D 、E .试猜想线段AD 、CE 、DE 的数量关系,并说明你的猜想理由.简析 猜想:AD +CE =DE .理由如下:由于OA 、OC 分别是∠BAC 、∠BCA 的平分线,DE ∥AC ,所以△ADO 和△CEO 均是等腰三角形,则DO =DA ,EC =EO ,故AD +CE =DE .例3 如图4,△ABC 中,AD 平分∠BAC ,E 、F 分别在BD 、AD 上,且DE =CD ,EF =AC .求证:EF ∥AB .简析 由于这里要证明的是EF ∥AB ,而AD 平分∠BAC ,所以必须通过辅助线构造出平行线,这样就可以得到等腰三角形了,于是DE =CD 的提示下,相当于倍长中线,即延长AD 至M ,使DM =AD ,连结EM ,则可证得△MDE ≌△ADC ,所以ME =AC ,又EF =AC ,∠M =∠CAD ,所以∠M =∠EFM ,即∠CAD =∠EFM ,又因为AD 平分∠BAC ,所以∠BAD =∠EFD =∠CAD ,所以EF ∥AB .二、利用角平分线+垂线,构造等腰三角形当一个三角形中出现角平分线和垂线时,我们就可以寻找到等腰三角形.如图5中,若AD 平分∠BAC ,AD ⊥DC ,则△AEC 是等腰三角形.例4 如图6,已知等腰R t△ABC 中,AB =AC ,∠BAC =90°,BF 平分∠ABC ,CD ⊥BD 交BF 的延长线于D .求证:BF =2CD .简析 由BF 平分∠ABC ,CD ⊥BD ,并在图5的揭示之下,延长线BA 、CD 交于点E ,于是△BCE 是等腰三角形,并有ED =CD ,余下来的问题只需证明BF =CE ,而事实上,由∠BAC =90°,CD ⊥BD ,∠AFB =∠DFC ,得∠ABF =∠DCF ,而AB =AC ,所以△ABF ≌△ACE ,则BF =CE ,故BF =2CD .E 图5ABCD 图6BF DE CA- 3 -三、利用转化倍角,构造等腰三角形当一个三角形中出现一个角是另一个角的2倍时,我们就可以通过转化倍角寻找到等腰三角形.如图7①中,若∠ABC =2∠C ,如果作BD 平分∠ABC ,则△DBC 是等腰三角形;如图7②中,若∠ABC =2∠C ,如果延长线CB 到D ,使BD =BA ,连结AD ,则△ADC 是等腰三角形;如图7③中,若∠B =2∠ACB ,如果以C 为角的顶点,CA 为角的一边,在形外作∠ACD =∠ACB ,交BA 的延长线于点D ,则△DBC 是等腰三角形.例5 如图8,在△ABC 中,∠ACB =2∠B ,BC =2AC .求证:∠A =90°. 简析 由于条件中有两个倍半关系,而结论与角有关,因此首先考虑对∠ACB =2∠B 进行技术处理,即作CD 平分∠ACB 交AB 于D ,过D 作DE ⊥BC 于E ,则由∠ACB =2∠B 知∠B =∠BCD ,即△DBC 是等腰三角形,而DE ⊥BC ,所以BC =2CE ,又BC =2AC ,所以AC =EC ,所以易证得△ACD ≌△ECD ,所以∠A =∠DEC =90°. 说明 本题也可以利用图7的②、③来构造等腰三角形求解.手脑并用巧解题图7 BC DA① ② BC DA③BCDAE 图8CBAD湖北毕保洪随着《课程标准》深入实施:“有效的数学学习活动不能单纯的依赖模仿与记忆,动手实验、自主探索与合作交流成为学习的重要方法”.因此,以等腰三角形为背景的动手操作、动脑设计的手脑并用的中考题悄然兴起.一、模拟画图例1已知在如图1的△ABC中,AB=AC,∠A=36°,仿照图1,请你再用两种不同的方法,将△ABC分割成3个三角形,使每个三角形都是等腰三角形(图2、图3供画图用,作图工具不限,不要求写出作法,不要求证明,但要标出所分得每个等腰三角形的内角度数).解:如图4、图5、图6、图7.此题不仅培养同学们的动手能力,而且考查同学们的发散思维能力.二、手脑并用例2在平面内,分别用3根、5根、6根…火柴,首尾依次相接可以搭成什么形状的三角形呢?通过尝试,列表如下所示:问: (1)4根火柴能搭成三角形吗?(2)8根、12根火柴分别能搭成几种不同形状的三角形?并画出图形.解:(1)4根火柴不能搭成三角形因为1+1=2不满足三边关系.(2)8根火柴能搭成等腰三角形,如图8;而12根能搭成等边三角形,如图9,或等腰三角形,如图10,或直角三角形,如图11.此题动手操作性强而且有助于培养同学们探究学习的学习习惯.三、动手剪裁例3在劳技课上老师请同学们在一张边长为16cm的正方形纸板上,剪下一个腰长为10cm的等腰三角形(要求等腰三角形至少有一条边在正方形的边上),请你帮助同学们画出剪裁的等腰三角形.解:分三种情况:①如图12,AE=AF=10cm,沿EF剪裁;②如图13,AE=AF=10cm,沿EF和AF剪裁;③如图14,AE=EF=10cm,沿AF和EF剪裁.- 5 -。
构造等腰三角形解题的五种途径

构造等腰三⾓形解题的五种途径2019-09-19等腰三⾓形是⼀类特殊的三⾓形,它的性质和判定在⼏何证明和计算中有着⼴泛的应⽤.有些⼏何图形中不存在等腰三⾓形,可根据已知条件和图形特征,通过添加适当的辅助线,巧妙构造等腰三⾓形,然后利⽤等腰三⾓形的性质使问题获解.⼀、利⽤⾓平分线+平⾏线,构造等腰三⾓形当⼀个三⾓形中出现⾓平分线,我们可以通过作平⾏线构造等腰三⾓形.如图1,AD是ABC的⾓平分线.①如图2,过点D作DE∥AC交AB于点E,则ADE是等腰三⾓形;②如图3,过点B作BE∥AC交AD的延长线于点E,则ABE是等腰三⾓形;③如图5,点E是AB边上⼀点,过点E作EF∥AC分别交AD、BC于点F、G,则AEF是等腰三⾓形;④如图4,点E是AB边上⼀点,过点E作EF∥AC,交AD的延长线于点F,交BC于点G,则AEF是等腰三⾓形;⑤如图6,过点C作CE∥AD交AB的反向延长线于点E,则ACE是等腰三⾓形;⑥如图7,点E是AC边上⼀点,过点E作EF∥AD,交AB的反向延长线于点F,交BC于点G,则AEF是等腰三⾓形.我们知道,等腰三⾓形的顶⾓平分线、底边上的中线和底边上的⾼互相重合,简称“三线合⼀”.现在的问题是:如果三⾓形⼀边上的中线与它的对⾓的⾓平分线重合,那么这个三⾓形是否是等腰三⾓形呢?答案是肯定的,现在就来证明这个定理.例1 如图8,ABC中,中线AD平分∠BAC.求证:AB=AC.分析:AD既是AC的中线,同时⼜是ABC的⾓平分线.联想到与⾓平分线和中线有关的辅助线,可过点B(或点C)作AC(或AB)的平⾏线.证明:如图9,延长AD⾄点E,使DE=AD.BD=CD,∠BDE=∠ADC,DE=AD,BDE≌CDA.BE=AC,∠E=∠CAD.⼜∠BAD=∠CAD,∠BAD=∠E.AB=BE.AB=AC.说明:本例也可过点D作DEAB,DFAC,垂⾜分别为E、F,如图10所⽰,从⾯积⼊⼿证明.⼆、利⽤⾓平分线+垂线,构造等腰三⾓形当⼀个三⾓形中出现⾓平分线时,我们也可以通过作垂线的⽅法构造等腰三⾓形.如图11,点E是∠ABC的⾓平分线AD上的⼀点,过点E作AD的垂线分别交AB、AC于点M、N,则AMN是等腰三⾓形.例2 如图12,在ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于D, CEBD,交BD的延长线于点E.求证:CE=BD.分析:由⾓平分线和垂线可以构造以BC为腰、∠ABC为顶⾓的等腰三⾓形.证明:如图12,延长CE交AB的反向延长线于点F.BD平分∠ABC,CEBD,由⾓平分线的对称性知CE=EF=CF.∠1+∠F =90°,∠2+∠F =90°,∠1=∠2.⼜AB=AC,∠BAD=∠CAF=90°,BAD≌CAF.BD=CF.CE=BD.三、利⽤中垂线,构造等腰三⾓形当⼀个三⾓形中出现⾼时,可以在⾼所在的边(或其延长线)上取⼀点,使⾼是该点与该边上三⾓形的⼀顶点组成的线段的中垂线,从⽽构造等腰三⾓形.如图13,AD是ABC的⾼.①如图14,在线段BC上取⼀点E使ED=DE,连结AE,则AEC是等腰三⾓形;②如图15,在线段BC的延长线上取⼀点E,使BD=DE连结AE,则ABE是等腰三⾓形.例3 如图16,在ABC中,ADBC于点D,∠B=2∠C.求证:AB+BD=CD.分析:由待证结论AB+BD=CD并结合已知条件“ADBC”,可构造以AB为腰、AD为底边上的⾼的等腰三⾓形.证明:在BC上取⼀点E,使BD=DE,连结AE,则ABE是等腰三⾓形.AB=AE,∠B=∠AED.⽽∠AED=∠C+∠CAE,且∠B=2∠C,∠C+∠CAE=2∠C.∠CAE=∠C.AE=CE.AB=CE.AB+BD=CE+DE=CD.四、利⽤平⾏线,构造等腰三⾓形过等腰三⾓形⼀腰上的点作底边或另⼀腰的平⾏线,都可以得到等腰三⾓形. 如图17,在ABC中,AB=AC.过线段AB上⼀点D 作DE∥BC,DF∥AC,分别交AC、BC于点E、F,则ADE和BDF都是等腰三⾓形.例4 如图18,ABC中,AB=AC,D是AB上⼀点,E是AC延长线上⼀点,且BD=CE,DE交BC于点F.求证:DF=EF.分析:由待证结论知点F是线段DE的中点,再结合已知条件“AB=AC”,可过点D作DM∥AC构造等腰三⾓形.证明:过点D作DM∥AC交BC于点M,则∠DMB=∠ACB,∠FDM=∠E.AB=AC,∠B=∠ACB.∠B=∠DMB.BD=DM.⼜BD=CE,DM=CE.在DMF和ECF中,DM=CE,∠FDM=∠E,∠DFM=∠EFC,DMF≌ECF.DF=EF.说明:本例也可过点E作EN∥AB交BC的延长线于点N,证明过程留给同学们完成.五、转化倍⾓,构造等腰三⾓形当⼀个三⾓形中出现⼀个⾓是另⼀个⾓的2倍时,我们就可以通过转化倍⾓寻找到等腰三⾓形.如图19,ABC中,∠B=2∠C.①如图20,作BD平分∠ABC,则DBC是等腰三⾓形;②如图21,延长CB到点D,使BD=BA,连结AD,则ADC是等腰三⾓形;③如图22,以C为⾓的顶点,CA为⼀边,在形外作∠ACD=∠ACB,交BA的延长线于点D,则DBC是等腰三⾓形.例5 如图23,在ABC中,∠ABC=2∠C,BC=2AB.求证:∠A=90°.分析:结合已知条件“∠ABC=2∠DBA”和“BC=2AB”,可作∠ABC的平分线BD交AC于点D,并取BC的中点E,连结DE,借助等腰三⾓形的“三线合⼀”和三⾓形全等证明.证明:作∠ABC的平分线BD交AC于点D,则∠DBE=∠C.BD=CD.取BC的中点E,连结DE,则BE=AB,且DEBC.在ABD和EBD中,BE=AB,∠DBE=∠DBA,BD=BD,ABD≌EBD.∠BED=∠A=90°.(作者单位:湖北省襄阳市襄州区黄集镇初级中学)注:本⽂为⽹友上传,不代表本站观点,与本站⽴场⽆关。
等腰三角形的五个模型

等腰三角形1.(1)已知:等腰三角形的一个内角为140°,那么另外两个角的度数为:__________(2)等腰三角形有一个内角是70,那么它的顶角为:__________(3)等腰三角形的周长为30,其中一边长为14,那么底边的长:__________(4)等腰三角形,它的两条边长分别为2和4,那么它的周长为:2.如图,在△ABC 中,∠ABC 和∠ACB 的平分线交于点O,过点O 作EF ∥BC,交AB于E,交AC 于F,AB=9,AC=8.求:(1)图中有几个等腰三角形,(2)AEF 的周长。
并说明理由。
模型一:角平分线+平行线→等腰三角形3、如图,已知BO 平分CBA ∠,CO 平分ACB ∠,MN BC ∥,且过点O ,若12AB =,14AC =,则AMN △的周长是 .4、如图2,△ABC 中,AB =AC ,在AC 上取点P ,过点P 作EF ⊥BC ,交BA 的延长线于点E ,垂足为点F .求证:AE =AP .5、如图3,在△ABC 中,∠BAC ,∠BCA 的平分线相交于点O ,过点O 作DE ∥AC ,分别交AB ,BC 于点D ,E .试猜想线段AD ,CE ,DE 的数量关系,并说明你的猜想理由.6、如图4,△ABC 中,AD 平分∠BAC ,E ,F 分别在BD ,AD 上,且DE =CD ,EF =AC .求证:EF ∥AB .模型二 角平分线+垂线→等腰三角形 当一个三角形中出现角平分线和垂线时,我们就可以寻找到等腰三角形.1、如图5中,若AD 平分∠BAC ,AD ⊥DC ,则△AEC 是等腰三角形.CA B E DO 图3图4 B F C D E A 图2 FB AC P E E 图5 A B CD2、如图6,已知等腰R t△ABC 中,AB =AC ,∠BAC =90°,BF 平分∠ABC ,CD ⊥BD 交BF 的延长线于D .求证:BF =2CD .模型三 作倍角的平分线→等腰三角形 当一个三角形中出现一个角是另一个角的2倍时,我们就可以作倍角的平分线寻找到等腰三角形.1、如图7中,若∠ABC =2∠C ,如果作BD 平分∠ABC ,则△DBC 是等腰三角形.2、如图8,△ABC 中,∠ACB =2∠B ,BC =2AC .求证:∠A =90°.模型四 “以角平分线为轴翻折”构造全等三角形 如图,在ABC △中,AD 平分BAC ∠,AB=AC+CD ,求:B C ∠:∠的值.模型五 “角平分线 + 垂线”构造全等三角形或等腰三角形1.根据角平分线的性质作垂线:自角的平分线上任意一点向角的两边作垂线,得到两个全等的直角三角形;2.根据等腰三角形的“三线合一”性质作垂线:自角的一边上任意一点作角平分线的垂线,使之与另一边相交,则截的一个等腰三角形.如图4,在四边形ABCD 中,BC BA >,AD DC =,BD 平分ABC ∠.求证:180A C ︒+=∠∠.图6 B F D C A C B 图7 D A 图8 C B A A B C D A B CD (图4)。
等腰三角形的五个模型(可编辑修改word版)

ODFA P B等腰三角形1.(1)已知:等腰三角形的一个内角为 140°,那么另外两个角的度数为:(2) 等腰三角形有一个内角是 70,那么它的顶角为: (3) 等腰三角形的周长为 30,其中一边长为 14,那么底边的长: (4) 等腰三角形,它的两条边长分别为 2 和 4,那么它的周长为: 2.如图,在△ABC 中,∠ABC 和∠ACB 的平分线交于点 O,过点 O 作 EF ∥BC,交 AB 于 E, 交AC 于 F,AB=9,AC=8求. :(1)图中有几个等腰三角形,(2)AEF 的周长。
并说明理由。
模型一:角平分线+平行线→等腰三角形3、如图,已知 BO 平分∠CBA , CO 平分∠ACB , MN ∥ BC ,且过点 O ,若 AB = 12 , AC = 14 ,则△AMN 的周长是 .4、如图2,△ABC 中,AB =AC ,在AC 上取点P ,过点P 作EF ⊥BC ,交BA 的延长线于点E ,垂足为点F .求证:E AE = AP .BCF 图 25、如图 3,在△ABC 中,∠BAC ,∠BCA 的平分线相交于点 O ,过点 O 作 DE ∥AC ,分别交 AB ,BC 于点 D ,E .试猜想线段 AD ,CE ,DE 的数量关系,并说明你的猜想理由.CEAB图 36、如图 4,△ABC 中,AD 平分∠BAC ,E ,F 分别在 BD ,AD 上,且 DE =CD ,EF =AC .求证:EF ∥AB .A模型二 角平分线+垂线→等腰三角形B C当一个三角形中出现角平分线和垂线时,我们就可以寻找到等腰三角形. ED1、如图 5 中,若 AD 平分∠BAC ,AD ⊥DC ,则△AEC 是等腰三角形.图 4AECD图 5A 2如、图6已,知等腰R t△ABC 中,AB =AC ,B ∠AC =90°,BF 平分∠AB C C ,D ⊥BD 交BF 的延长线于D .求F D1BC图 6DA D证B :F =2CD .模型三 作倍角的平分线→等腰三角形当一个三角形中出现一个角是另一个角的 2 倍时,我们就可以作倍角的平分线寻找到等腰三角形. 1、如图 7 中,若∠ABC =2∠C ,如果作 BD 平分∠ABC ,则△DBC 是等腰三角形.ABC图 72、如图 8,△ABC 中,∠ACB =2∠B ,BC =2AC .求证:∠A =90°.ABC 图 8模型四 “以角平分线为轴翻折”构造全等三角形A如图,在△ABC 中, AD 平分∠BAC ,AB=AC+CD ,求: ∠B : ∠C 的值.CBD模型五 “角平分线 + 垂线”构造全等三角形或等腰三角形1. 根据角平分线的性质作垂线:自角的平分线上任意一点向角的两边作垂线,得到两个全等的直角三角形;2. 根据等腰三角形的“三线合一”性质作垂线:自角的一边上任意一点作角平分线的垂线,使之与另一边相交,则截的一个等腰三角形.如图 4,在四边形 ABCD 中, BC > BA , AD = DC , BD 平分∠ABC . 求证:∠A +∠C = 180︒ .BC(图 4)2。
小专题构造等腰三角形的常用技巧人教版八年级数学上册作业课件PPT

技巧一:作平行线构造等腰三角形 【模型构建】 ①利用“角平分线+平行线”构造等腰三角形.若∠1=∠2,AC∥ OB,则△OAC 为等腰三角形.
②作腰的平行线构造等腰三角形.若 AB=AC,DE∥AC形.若 AB=AC,DE∥BC,则△ADE 为等腰三角形.
小专题(5) 构造等腰三角形的常用技巧-2020秋人 教版八 年级数 学上册 作业课 件(共20 张PPT)
小专题(5) 构造等腰三角形的常用技巧-2020秋人 教版八 年级数 学上册 作业课 件(共20 张PPT)
5.如图,在△ABC 中,AD 为中线,E 为 AB 上一点,AD,CE 交 于点 F,且 AE=EF,求证:AB=CF.
证明:在边 AC 上截取 AP=AB,连接 PD. ∵AD 是∠BAC 的平分线,∴∠BAD=∠PAD. ∴△ABD≌△APD(SAS). ∴∠APD=∠B,PD=BD. ∵∠B=2∠C,∠APD=∠PDC+∠C, ∴∠PDC=∠C. ∴PD=PC.∴BD=PC. ∴AB+BD=AP+PC=AC.
小专题(5) 构造等腰三角形的常用技巧-2020秋人 教版八 年级数 学上册 作业课 件(共20 张PPT)
小专题(5) 构造等腰三角形的常用技巧-2020秋人 教版八 年级数 学上册 作业课 件(共20 张PPT)
1.如图,AE,BC 交于点 D,且 AB=CE,∠B+∠DCE=180°, 求证:AD=DE.
小专题(5) 构造等腰三角形的常用技巧-2020秋人 教版八 年级数 学上册 作业课 件(共20 张PPT)
∴∠G=∠EAF. ∵AE=EF, ∴∠EAF=∠EFA=∠GFC. ∴∠G=∠GFC,∴CG=CF.∴AB=CF. 方法二:延长 AD 至 M,使 DM=DF,连接 BM, 同理可证 CF=BM=AB. 方法三:作 BM⊥AD 于 M,CN⊥AD 于 N, 先证△BMD≌△CND,BM=CN, 再证△ABM≌△FCN 即可.
构造等腰三角形解题方法论

构造等腰三角形解题方法论山东沂源县徐家庄中心学校256116 左效平等腰三角形是一种特殊的三角形,它的性质和判定在计算和证明中有着广泛的应用.当图形中无显性的等腰三角形时,可根据条件和图形的特征,适当添加辅助线,如延长线,平行线等等,直接构造等腰三角形或判定三角形是等腰三角形,后利用等腰三角形的性质,破解问题.1.延长线段法直接构造等腰三角形例1 如图1,已知在△ABC中,AD平分∠BAC,∠B=2∠C.求证:AB+BD=AC.图 1分析:延长AB到点E,使得BE=BD,只需证明△ADE≌△ADC,结论得证.证明:延长AB到点E,使得BE=BD,连接DE,因为BE=BD,所以∠ABC=2∠E.因为∠ABC=2∠C,所以∠C=∠E.所以DAE DACE CDA DA∠=∠⎧⎪∠=∠⎨⎪=⎩,所以△ADE≌△ADC,所以AC=AE.因为AE=AB+BE,所以AB+BD=AC.点评:延长较长的线段,使得延长线段等于较短的线段,从而把折线段的和转化为共线线段的和,设法证明构造的新线段与所求和线段相等即可.这是证明这类问题的一种常用方法要熟练掌握.例2 如图2,已知在△ABC中,AB=AC,∠A=90°,BD平分∠ABC.求证:BC=AB+AD.图 2分析:注意等腰直角三角形锐角为45°.证明:延长AB到点E,使得AE=AD,连接DE,因为AE=AD,AB=AC,∠A=90°,所以∠C=∠E=45°.所以EBD CBDE CDB DB∠=∠⎧⎪∠=∠⎨⎪=⎩,所以△BDE≌△BDC,所以BC=BE.因为BE=AB+AE,所以BC=AB+AD.点评:熟记等腰直角三角形锐角为45°是解题的重要因素.2.延长线段法先判断等腰三角形后证不等式例3 如图3,已知,在△ABC中,AD是边BC上的中线,DE平分∠ADB,DF平分∠ADC,连接EF. 求证:EF<BE+CF.图 3分析:延长ED到点G,使得ED=DG,则DF是三角形EFG的中线,根据DE平分∠ADB,DF平分∠ADC,可以得到DF⊥EG,从而判断三角形EFG是等腰三角形,把EF迁移到 FG的位置上,利用三角形全等的性质,把BE迁到CG的位置上,利用三角形的三边关系定理即可破解.证明:延长ED到点G,使得ED=DG,因为DE平分∠ADB,DF平分∠ADC,所以DE⊥DF,连接FG,则三角形EFG是等腰三角形,所以EF=FG.连接CG,因为DE DGEDB CDG DB DC=⎧⎪∠=∠⎨⎪=⎩,所以△ADE≌△ADC,所以CG=BE.因为FG<CG+CF,所以EF<BE+CF.点评:通过构造等腰三角形把不共三角形的线段迁移到同一三角形中,这也是解题的重要思路.3.延长线段法先判断等腰三角形后证等量关系例4 如图4梯形ABCD中,AD∥BC,点E是CD的中点,且AE⊥BE.求证:AB=AD+BC.图 4分析:延长AE,BC交于点F,易证AE=EF,为解题补充条件,结合已知条件AE⊥BE,轻松得到等腰三角形ABF,应用等腰三角形的性质,全等三角形的性质,问题轻松破解.解:延长AE,BC交于点F,所以DAE CFEADE FCEDE CE∠=∠⎧⎪∠=∠⎨⎪=⎩,所以△ADE≌△FCE,所以AE=EF,AD=CF,因为AE⊥BE,所以AB=BF,因为BF=BC+CF,AD=CF,所以AB=AD+BC.点评:熟练判断三角形ABF是等腰三角形是解题的关键.灵活应用等腰三角形的性质,全等三角形的性质也是解题的重要依据.4.延长等腰梯形的两腰构造等腰三角形例5 已知,如图5,在等腰梯形ABCD中,AD∥BC,AB=CD,P是BC上的一点,PE⊥AB,PF⊥CD,BG⊥CD,垂足分别是E,F,G,求证:BG=PE+PF.图 5分析:同一个图形的面积相同,且整体图形的面积等于分割后几个部分图形的面积和,这也是解答此类问题常用的方法---面积法.证明:如图5,延长BA,CD交于点M,连接PM.因为四边形ABCD是等腰梯形,所以三角形MBC是等腰三角形,所以MB=MC.三角形MBC的面积=21×MC×BG,三角形MPB的面积=21×MB×PE,三角形MPC的面积=21×MC×PF,且三角形MBC的面积=三角形MPB的面积+三角形MPC 的面积, 所以21×MC ×BG=21×MB ×PE +21×MC ×PF=21×MC (PE+PF ),所以所以BG=PE+PF .点评:面积法能帮助我们解答很多类型的问题,希望能重视这种解题方法.5.平行线+角平分线构造等腰三角形 例6 如图6,在平行四边形ABCD 中,BE 平分∠ABC,交边AD 于点E. 求证:BC=CD+DE .图 6分析:证明AB=AE 是解题的关键. 证明:因为四边形ABCD 是平行四边形, 所以AD ∥BC,AD=BC,AB=CD , 因为BE 平分∠ABC, 所以∠ABE=∠AEB , 所以AB=AE , 所以AD=AE+ED , 所以BC=AB+ED , 所以BC=CD+DE .点评:角平分线和平行线相遇易生成一个等腰三角形,这是解题的一个关键.6.垂直+角平分线构造等腰三角形例7 如图7,(第26届希望杯初二试题) 在四边形ABCD 中,AC 平分∠DAB,AD=9,BC=CD=10,AB=21, 则AC= .图 7分析: AC 平分∠DAB,作DE ⊥AC ,垂足为G ,交AB 于点E ,连接CE ,可判断三角形ADE 是等腰三角形,三角形CDE 是等腰三角形,这样就为解题创造了条件,提供了一条求解的思路.解:作DE ⊥AC ,垂足为G ,交AB 于点E ,连接CE ,AC 平分∠DAB, 所以AD=AE=9,CD=CE=CB=10, 因为AB=21,所以EB=12.作CF ⊥AB ,垂足为F ,交AB 于点F ,则EF=FB=6.在直角三角形BCF 中,BC=10,所以CF=8.在直角三角形ACF 中,AF=AE+EF=9+6=15,CF=8,所以AC==17.点评: 正确构造两个等腰三角形是解题的关键.例8 如图8,已知△ABC 中,AB=AC, ∠BAC=90°,BD 平分∠ABC ,交AC 于点D ,CE ⊥BE ,垂足为E ,求证:BD=2CE.图 8分析:BE 平分∠CAB,CE ⊥BE ,延长CE,交BA 的延长线于点F ,可判定三角形BCF 是等腰三角形,CE=EF.只需证明BD=CF,问题就顺利得证.证明:延长CE,交BA的延长线于点F,BE平分∠CAB,CE⊥BE,所以CE=EF,所以CF=2CE.易证Rt△BAD≌Rt△CAF,所以BD=CF,所以BD=2CE.点评:构造等腰三角形BCF是证明的关键.7.梯形中构造等腰三角形例9 如图9,已知AC∥BD, EA、EB分别平分∠CAB,∠ABD,CD经过点E,求证:AB=AC+BD.图9分析 AC∥BD, EA、EB分别平分∠CAB,∠ABD,可知AE⊥BE,AE平分∠CAB,延长BE,交AC的延长线于点F,可判定三角形ABF是等腰三角形,故AB=AF=AC+CF,易证CF=BD.问题得证.证明:延长延长BE,交AC的延长线于点F,由AC∥BD, EA、EB分别平分∠CAB,∠ABD,可知AE⊥BE,所以AF=AB,BE=EF.易证△EFC≌Rt△EBD,所以BD=CF.由AF=AC+CF,所以AB=AC+BD.点评:构造等腰三角形ABF是证明的关键.。
等腰三角形八大几何模型与九类题型(模型梳理与题型分类讲解)(人教版)(学生版)25学年八年级数学上册
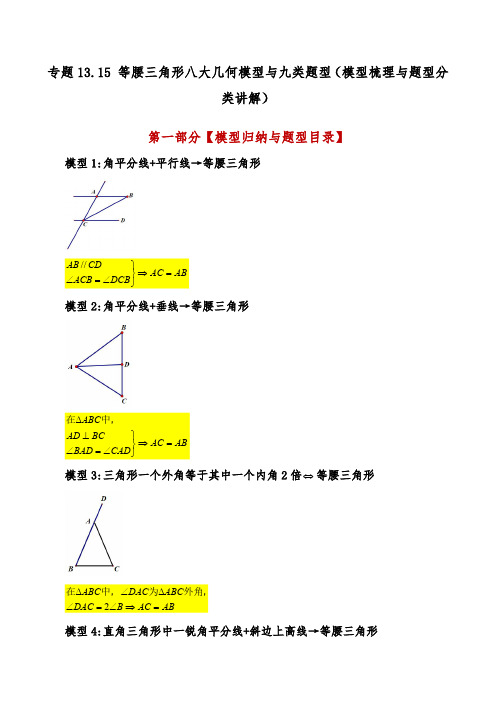
专题13.15等腰三角形八大几何模型与九类题型(模型梳理与题型分类讲解)第一部分【模型归纳与题型目录】模型1:角平分线+平行线→等腰三角形AB AC DCB ACB CDAB =⇒⎭⎬⎫∠=∠//模型2:角平分线+垂线→等腰三角形AB AC CAD BAD BCAD ABC =⇒⎭⎬⎫∠=∠⊥∆中,在模型3:三角形一个外角等于其中一个内角2倍⇔等腰三角形ABAC B DAC ABC DAC ABC =⇒∠=∠∆∠∆2外角,为中,在模型4:直角三角形中一锐角平分线+斜边上高线→等腰三角形CE CD CBD ABD AB CH ACB ABC =⇒⎭⎬⎫∠=∠⊥=∠∆,900中,在模型5:等边三角形中含定角问题60=∠⇒=∆AFE CE BD AC BC E D ABC 上的两个动点、是、中,在等边模型6:等边三角形中含“手拉手”AEBD AE BD DCE ABC =⇒∆∆、中,连接和等边在等边模型7:倍半角+角平分线→等腰三角形DC DB CBD ABD ACB ABC ACB ABC =⇒⎭⎬⎫∠=∠∠=∠=∠∆2900中,在模型8:倍长中线构造等腰三角形题型目录【题型1】角平分线+平行线→等腰三角形 (3)【题型2】角平分线+垂线(中线)→等腰三角形 (4)【题型3】三角形一个外角等于其中一个内角2倍⇔等腰三角形 (4)【题型4】直角三角形中一锐角平分线+斜边上高线→等腰三角形 (5)【题型5】等边三角形中含定角问题 (6)【题型6】等边三角形中含“手拉手” (7)【题型7】倍半角+角平分线→等腰三角形 (8)【题型8】倍长中线构造等腰三角形 (9)【题型9】拓展延伸 (9)第二部分【题型展示与方法点拨】【题型1】角平分线+平行线→等腰三角形【例1】(2024九年级下·浙江·专题练习)如图,在ABC V 中,AD 平分BAC ∠,AD BD ⊥于点D ,DE AC ∥交AB 于点E ,若8AB =,则DE =.【变式1】(2024·湖南娄底·模拟预测)如图,在ABC V 中,AD 平分CAB ∠,ED AB ∥.若ED CD =,15EAD ∠=︒,则ADB ∠等于()A .75︒B .60︒C .45︒D .90︒【变式2】(23-24八年级上·天津滨海新·期中)如图,在ABC V 中,ACB ∠的平分线交AB 于点E ,CF 平分ACD ∠,且EF BC ∥交AC 于点G ,若5cm CG =,则EF =cm .【题型2】角平分线+垂线→等腰三角形【例2】(23-24八年级上·福建龙岩·阶段练习)如图,在ABC V 中,CD 平分ACB ∠,CD BD ⊥,垂足为D ,180A CBD ∠+∠=︒,若5BD =,则AB 的长为()A .7B .8C .9D .10【变式1】(23-24八年级上·黑龙江哈尔滨·期中)如图,D 为ABC V 内一点,CD 平分ACB ∠,BE CD ⊥,垂足为D ,交AC 于点E ,A ABE ∠=∠,11AC =,7BC =,则BD 的长为()A .1B .1.5C .2D .2.5【变式2】(23-24八年级上·四川宜宾·期末)如图,CE 平分ACB ∠且CE DB ⊥于E ,DAB DBA ∠=∠,若14AC =,CDB △的周长为20,则DB 的长为.【题型3】三角形一个外角等于其中一个内角2倍⇔等腰三角形【例3】(23-24八年级上·吉林长春·期中)如图,在1ABA △中,1AB A B =,20B ∠=︒.在1A B 上取一点C ,延长1AA 到点2A ,使121A A AC =,连结2A C ;在2A C 上取一点D ,延长12AA 到点3A ,使232A A A D =,连结3A D ;……,按此操作进行下去,在以点5A 为顶角顶点的等腰三角形的底角的度数为()A .20︒B .10︒C .5︒D .2.5︒【变式1】(23-24八年级上·江苏盐城·期中)如图,在ABC V 中,BD BC =,AE AC =,100ACB ∠=︒,则DCE ∠的大小为.【变式2】(23-24八年级上·全国·单元测试)如图,在ABC V 中,AB AC =,36A ∠= ,BD 平分ABC ∠交AC 于点D ,DE AB ∥交BC 于点E ,EF BD ∥交CD 于点F ,则图中等腰三角形共有()A .5个B .6个C .7个D .8个【题型4】直角三角形中一锐角平分线+斜边上高线→等腰三角形【例4】(21-22八年级上·黑龙江哈尔滨·期中)如图,在ABC V 中,90BAC ∠=︒,30C ∠=︒,高AD 与角平分线BE 相交于点F .(1)求证:AEF △是等边三角形;(2)若2AE =,求AD 的长度.【变式1】(24-25八年级上·全国·假期作业)如图,在ABC V 中,90ACB ∠=︒,CD 是AB 边上的高,AE 是BAC ∠的角平分线,AE 与CD 交于点F ,求证:CEF △是等腰三角形.【变式2】(22-23八年级下·湖南永州·期末)如图,ABC V 中,90BAC AD BC ABC ∠=︒⊥∠,,的平分线BE 交AD 于点F ,AG 平分DAC ∠.给出下列结论:①BAD C ∠=∠;②AEF AFE ∠=∠;③EBC C ∠=∠;④AG EF ⊥;⑤AB GB =.正确结论有()个.A .2B .3C .4D .5【题型5】等边三角形中含定角问题【例5】(2024七年级下·上海·专题练习)如图,等边ABC V 中,=AD CE ,BD 和AE 相交于F ,BG AE ⊥垂足为G ,求FBG ∠的度数.【变式1】(23-24八年级下·河南郑州·期末)已知:如图,点D ,E 分别是等边三角形ABC 的两边AB AC ,上的点,且=AD CE .(1)求证:ADC CEB △≌△;(2)求BPC ∠的度数.【变式2】(2024·浙江杭州·二模)如图,ABC V 是等边三角形,D ,E 分别是AC ,BC 边上的点,且=AD CE ,连接BD ,AE 相交于点F ,则下列说法正确的是()①ABD CAE ≌ ;②60BFE ∠=︒;A .①B .②C .①②D .都错【题型6】等边三角形中含“手拉手”【例6】(23-24八年级下·陕西西安·阶段练习)如图所示,A 、C 、B 三点共线,DAC △与EBC 都是等边三角形,AE BD 、相交于点P ,且分别与CD CE 、交于点M ,N .(1)求证:ACE DCBV V ≌(2)求APD ∠的度数【变式1】(2024·重庆南岸·模拟预测)如图,,ABC CDE △△都是等边三角形,将CDE 绕点C 旋转,使得点,,A D E 在同一直线上,连接BE .若1,4BE AE ==,则CE 的长是.【变式2】(23-24八年级上·福建南平·期末)如图,ABC V 和ADC △都是等边三角形,点E ,F 分别在边BC 和CD 上,且60EAF ∠=︒,若AEF △的周长最小时,则BAE ∠的大小是.【题型7】倍半角→等腰三角形【例7】(22-23八年级上·北京·期中)如图,在ABC V 中,90ABC ∠=︒,D 为AB 上一个动点.(1)已知2A BCD ∠=∠,求证:2AD AC AB +=.下面是两位同学分享的思路:小快同学:从求证目标出发,倍长AB 到E ,即2AE AB =,又AE AD DE =+,则只需证DE AC =.小乐同学:从已知条件角的关系出发,发现若将BCD △关于直线BC 对称得到BCF V ,则可证ACF △为等腰三角形.请你选择一种思路,完成证明(2)已知AB BD AC +=,ACD α∠=,请直接写出A ∠的大小(用含α式子表示).【变式1】(23-24八年级上·黑龙江哈尔滨·期末)如图,ABC V 中,2C B ∠=∠,,AD AE 分别为ABC V 的高,角平分线,下列四个结论:①AC CD BD +=;②AC CD AB +=;③AC CE AB +=;④2B DAE ∠=∠.其中所有正确结论的序号是.【题型8】倍长中线构造等腰三角形模型【例8】(23-24八年级上·湖北武汉·期中)如图,A 是ABC 的中线,E 是A 上一点,BE 交AC 于F ,若EF AF =,8BE =,5CF =,则EF 的长度为()A .1.5B .2C .2.5D .3【变式】(22-23八年级上·湖北武汉·期中)如图,在ABC V 中,D 是BC 的中点,E 是AD 上一点,BE AC =,BE 的延长线交AC 于点F ,若60ACB ∠=︒,44DAC ∠=︒,则求FBC ∠的度数为.第三部分【拓展延伸】【题型9】拓展延伸【例1】(23-24八年级上·北京·期末)如图,ABC V 中,BF CF 、分别平分ABC ∠和ACB ∠,过点F 作DE BC ∥交AB 于点D ,交AC 于点E ,那么下列结论:①DFB DBF ∠=∠;②EFC 为等腰三角形;③ADE V 的周长等于BFC △的周长;④1902BFC A ∠∠=+ .其中正确的是【例2】(23-24八年级上·上海普陀·期末)【图形新发现】小普同学发现:如果一个三角形的一条角平分线与一条中线互相垂直,那么这个三角形的某两条边必有倍半关系.如图1,已知在ABC V 中,BD 是ABC V 的角平分线,AE 是ABC V 的中线,AE BD ⊥,垂足为点F .(1)根据图1,写出ABC V 中小普同学所发现的结论,并给出证明;【图形再探究】现将小普同学所研究的三角形称为“线垂”三角形,并将被这条内角平分线所平分的内角叫做“分角”.下面我们跟着小普同学再探究:(2)在如图1中,“线垂”三角形ABC 是否可以是直角三角形?如果可以,求DBC ∠的度数;如果不可以,请说明理由;(3)已知线段MN ,是否存在一点P ,使得以MN 为一边的“线垂”三角形PMN 为等腰三角形?如果存在,请在图2中用直尺和圆规做出PMN ∠为“分角”的“线垂”等腰三角形PMN (不写作法,仅保留作图痕迹,在图中清楚地标注出点P ),并用文字语言归纳表述成一条与“线垂”等腰三角形的边或角有关的真命题;如果不存在,请说明理由.。
专题:构造等腰三角形的常用方法(1)

专题:构建等腰三角形的常用方法类型一:作腰或底的平行线构造等腰三角形解题思路:在等腰三角形内部或外部作任意一边的平行线均可构造等腰三角形。
基本模型:已知:在^ ABC中,AB=AC D是直线AB上一点。
例题1:如图,在△ ABC中,AB=AC E是AB上一点,F是AC延长线上一点,且BE=CF连接EF交BC于点D。
求证:DE=DF练习:如图,过等边三角形ABC的边AB上一点P,Q为BC延长线上一点,且PA=CQ连接PQ交AC于点D。
求证:PD=DQ类型二:利用“角平分线 +平行线”构造等腰三角形解题思路:当一个三角形出现角平分线时,可以通过作平行线构造等腰三角形。
例题2:如图,在四边形ABCD 中,AB// DC,虚BC 的中点,AE 是/ BAD 的角平分线。
类型三:利用“角平分线 +垂线”构造等腰三角形解题思路:当一个三角形出现角平分线时,可以通过作垂线构造等腰三角形。
基本模型:如图:在^ ABC 中,AD 是/ BAC 的角平分线。
例题3:如图,在^ ABC 中,已知SA ABC =12, AD 平分/ BAC 且AD± BD 于点D 。
A基本模型:如图:在4 ABC 中,AD 是/ BAC 的角平分线。
求证:AD=DC+AB类型四:利用倍角关系构造等腰三角形解题思路:当一个三角形中出现一个角是另一个角的2倍时,可以通过转化倍角,构造等腰三角B=2/ Co例题4:如图,在△ ABC中,/ B=2/ C, AD是/ BAC的角平分线。
求证:AB+BD=AC练习:如图,在△ ABC中,/ C=2Z A , AC=2BC求证:/ B=90°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
列举构造等腰三角形4种常用方法模型
1. 构造等腰三角形的一个底角:
已知等腰三角形的一个底角,我们可以使用圆规和直尺来构造等腰三角形的另一条底边和另一个底角。
2. 利用中垂线构造等腰三角形:
已知线段的中点,我们可以使用中垂线性质来构造等腰三角形。
3. 利用平行线构造等腰三角形:
已知一条直线和该直线外的一点,我们可以使用平行线性质来构造等腰三角形。
4. 利用角平分线性质构造等腰三角形:
已知一个角的角平分线,我们可以使用角平分线性质来构造等腰三角形。
