保险精算与寿险精算
保险精算与寿险精算

保险公司风险管理策略
保险公司风险管理的实践
• 根据寿险精算的风险测度和风险管理策略制定风险管理
• 实施风险分散、风险控制和风险转移等风险管理措施
计划
• 通过保险合同和保险条款限制控制风险
• 考虑保险公司的风险承担能力和市场需求
05
保险精算与寿险精算的未来发
展趋势
保险精算与大数据技术的结合
大数据技术在保险精算中的应用
• 为保险公司的产品策略和风险管理提供依据
寿险精算在养老金规划中的应用
养老金规划的精算方法
养老金规划的产品设计
• 根据寿险精算的生命表和利率模型进行养老金需求预测
• 设计多样化、个性化的养老金规划产品
• 考虑投保人的养老金需求和风险承受能力
• 适应保险市场的变化和客户需求的多样化
寿险精算在保险公司风险管理中的应用
• 利率模型对寿险产品的定价和评估具有重要影响
寿险精算中的风险测度与风险管理
寿险精算中的风险测度
寿险精算中的风险管理策略
• 风险损失分布:描述保险事故损失的不确定性
• 风险分散:通过投资组合实现风险分散
• 风险度量:如标准差、风险指数等指标衡量风险大小
• 风险控制:通过保险条款和保险金额限制控制风险
• 风险控制:为保险公司提供风险管理策略和建议
保险精算的核心理念
• 谨慎经营:确保保险公司的长期稳健发展
• 公平性:使保险产品的风险和收益在投保人和保险公司之间合理分配
寿险精算的起源与发展
寿险精算的起源
• 17世纪英国:生命表的概念引入保险领域
• 19世纪法国:寿险精算学派的形成
寿险精算的发展
• 20世纪初:美国寿险精算师协会的成立
什么是保险精算

一、保险精算保险精算是依据经济学的基本原理和知识,利用现代数学方法,对各种保险经济活动未来的财务风险进行分性、估价和管理的一门综合性的应用科学。
如研究保险事故的出险规律、保险事故损失额的分布规律、保险人承担风险的平均损失及其分布规律、保险费率和责任准备金、保险公司偿付能力等保险具体问题。
所谓精算,就是运用数学、统计学、金融学及人口学等学科的知识和原理,去解决工作中的实际问题,进而为决策提供科学依据。
二、精算学的学科发展和框架在分析精算学的起源时,英国精算师协会将最早的精算思想的萌芽设定在甚至是古埃及和古罗马时期。
保险精算的理论基础1.利息理论与概率论的出现17 世纪,个人风险问题开始引起社会的关注,相应的愈来愈多的数学家开始为个人风险的解决寻找数理基础。
利息理论(当时主要是复利理论) 解决了保险资金和养老金资金在未来的投资收益问题,为远期支出要求在当期负担的量化问题提供了理论基础; 随着1657 年荷兰数学家Christian Huygens 的一篇小论文De Ratiocinics in Ludo Aleae的发表,概率论产生了。
2.生命表的出现及精算学的产生保险精算的产生是以哈雷慧星的发现者,英国天文学家哈雷(Halley)在1693年发表的世界上第一张生命表为标志,至今已有三百多年的历史。
最为关键的是: Halley 应用自己的生命表对于特定年龄的投保人的年金型保险产品的负担金额进行了测算。
他将自己测算的未来各年度的死亡率结合各年度的货币收入来综合考察,并注意考察了各年度货币收入的利息率的影响,也即考察了各年度预期货币收入的现值(即后来的精算现值, Act uarial Present Value ,APV) ,将各年度的值加总就得出了该保险产品的当期货币价值。
精算学也由此产生。
3.精算学的发展(1)精算理论的应用和精算师、精算(师) 协会的产生成立于1762 年的The Equi2table (伦敦公平保险社) 是第一家应用精算技术来厘定保险费率的寿险公司。
保险精算课程三(寿险精算)
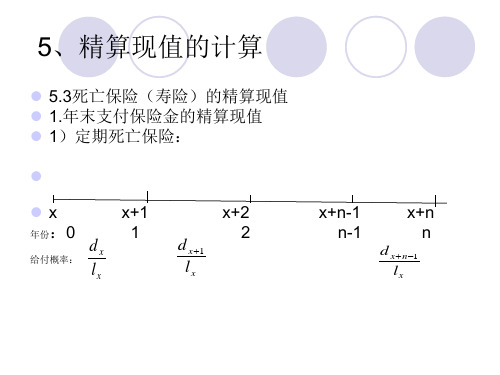
x
xn
x
xh
2.终身寿险的年缴纯保费
h Px
Ax ax:h|
Mx Nx Nxh
3.两全保险的年缴纯保费
P h x:n|
Ax:n| ax:h |
Mx
M xn Dxn Nx Nxh
课堂练习:
1.某人30岁投保20年期,延期10年,5年限期缴费的定期 人寿险,保险金额为100000元,求年缴纯保险费?
N x N x1 Dx
S x N x N x1
(Ia) x
Sx Dx
( Ia) x
S x 1 Dx
( Ia) x:n |
S x 1
S x n1 Dx
nN x n1
作业:
1.某人30岁(女)时投保寿险,约定45岁前死亡给付保险金 150000元,40岁至60岁之间死亡给付保险金为100000 元,60岁以后给付保险金50000元,求趸缴纯保险费?
(In| A)x (IA)1x:n| n|Ax
Rx Rxn nM xn N M xn
Dx
Dx
标准递减也可以看作:
A1 x:n |
A1 x:n 1|
A1 x:n 2|
A1 x:1|
nM x [Rx1 Rxn1 ] Dx
课堂练习
(x)=30,定期寿险保单。第一年死亡给付1000元, 第二年死亡给付1200元,第三年1400元,这样依次按 200元比例递增,n=20,求保险金的精算现值:
x:n |
Dx
Ax:n|
Mx
M xn Dx
Dxn
Ax
Mx Dx
m| Ax
M xm Dx
A1 x :n|
Mx
M Dx
保险精算与寿险精算

保险精算与寿险精算简介保险精算和寿险精算是保险行业中重要的技术领域。
保险精算主要涉及对保险风险的评估和定价,而寿险精算则着重于寿险产品和策略的设计和管理。
本文将对保险精算和寿险精算进行详细说明,并介绍其在保险业务中的作用和价值。
1. 保险精算1.1 什么是保险精算保险精算是一门利用数学和统计方法,对保险风险进行评估和量化的技术。
通过分析历史数据和建立风险模型,保险精算师能够确定合理的保险费率,并评估保险产品的盈利潜力和风险状况。
1.2 保险精算的重要性保险精算在保险行业中具有重要的作用和价值。
首先,保险精算可以帮助保险公司制定合理的保险费率,确保公司的盈利和长期的可持续发展。
其次,保险精算可以帮助保险公司评估和管理风险,降低风险对公司的影响。
最后,保险精算还可以提供决策支持,帮助保险公司做出明智的业务决策。
1.3 保险精算的方法和技术保险精算涉及多种方法和技术,包括但不限于:•统计分析:通过分析历史数据和建立风险模型,评估保险风险和损失概率。
•寿命表分析:利用寿命表和生命表,对人寿保险产品进行评估和定价。
•赔付分析:通过对赔付数据进行分析,评估赔付风险和赔付概率。
•风险模型:建立风险模型,对不同风险因素进行量化和评估。
•金融数学模型:运用金融数学理论和方法,对投资风险和资本需求进行评估。
2. 寿险精算2.1 什么是寿险精算寿险精算是保险精算的一个分支,专注于寿险产品和策略的设计和管理。
寿险精算的目标是通过评估寿险风险和损失,确定合理的保费、保额和保险期限,为寿险产品提供精确的定价和销售策略。
2.2 寿险精算的重要性寿险精算对于寿险公司而言具有重要的意义。
首先,寿险精算可以帮助寿险公司评估和管理寿险风险,确保公司的稳定发展。
其次,寿险精算可以帮助寿险公司设计和定价寿险产品,满足客户需求并确保公司的盈利。
最后,寿险精算还可以帮助寿险公司进行业务决策,提供决策支持和合理的销售策略。
2.3 寿险精算的方法和技术寿险精算使用了多种方法和技术,包括但不限于:•寿命表分析:利用寿命表和生命表,对寿险风险和赔付概率进行评估和量化。
保险精算学寿险精算现值

K的概率分布函数为 : P K k k px qxk k qx.
故
Ax E Z vk 1 k qx .
k 0
在上式两边同乘lx , 得到lxBiblioteka Ax vk 1 d xk . k 0
给出直观解释.
引入转换函数:
D x v xlx, x岁 存 活 人 数 每 人 1单 位 元 在 0岁 的 现 值 ;
N x D x t , 从 x岁 起 到 生 命 最 大 值 1岁 上 存 活 t0
人 每 人 每 年1单 位 元 赔 付 在 0岁 的 现 值 。
Cx
v
x
1
d
,
x
x
x 1岁 死 亡 的 人 数 每 人 1 单 位 元 赔
付 在 0岁 的 现 值 ;
M x
C
x
,
t
从
x岁
起
到
生
命
最
大
值
4、延期n年的终身寿险
延期n年的终身寿险:用n Ax表示,某人x岁开始投保,延期n年 后死亡年末给付1单位元的延期终身寿险的现值。 现值随机变量为:
0 Z vK1
K 0,1,...,n1 K n,n1,.......
n Ax E
Z
vk1 k
kn
qx
Mxn Dx
或者
n
Ax
Ax
A1 x:n
证明:n Ax vn n pxAxn
1岁
上
每
人
t0
1单 位 元 赔 付 在 0岁 的 现 值 。
则
Ax
Mx Dx
对于赔付现值随机变量Z,计算方差:
VarZ EZ2 [EZ]2
2Ax E Z2 v2k1 k qx e2k1 k qx
保险精算与寿险精算

保险精算与寿险精算1. 引言保险精算是保险行业中非常重要的一项工作,它涉及到精确评估和管理保险风险的过程。
在保险精算中,寿险精算是其中的一个重要领域。
本文将介绍保险精算和寿险精算的根本概念,以及它们在保险行业中的应用和重要性。
2. 保险精算的概念保险精算是指利用数学、统计学和金融理论等工具来评估保险风险,并制定相关策略和决策的过程。
它是一个综合性的领域,结合了风险管理、投资管理和产品设计等方面的知识。
保险精算主要包括风险评估、风险定价、准备金计算和资产负债管理等内容。
3. 寿险精算的概念寿险精算是保险精算领域中的一个重要分支,它专注于寿险产品的精确评估和管理。
寿险精算的主要任务是对寿险风险进行定量分析,并为保险公司提供相应的精算建议。
寿险精算涉及到寿险保费的定价、寿险责任准备金的计算、赔付率的预测等内容。
4. 保险精算和寿险精算的应用保险精算和寿险精算在保险行业中有着广泛的应用。
首先,保险精算和寿险精算能够帮助保险公司评估和管理保险风险,从而提供准确的保险产品定价和风险控制策略。
其次,保险精算和寿险精算还可以为保险公司提供准备金计算和资产负债管理等方面的指导,帮助保险公司保持良好的财务稳定性。
此外,保险精算和寿险精算还可以帮助保险公司优化投资组合,提高资产的回报率。
5. 保险精算和寿险精算的重要性保险精算和寿险精算在保险行业中的重要性不言而喻。
首先,保险精算和寿险精算能够帮助保险公司评估和管理保险风险,从而降低保险公司的风险暴露。
其次,保险精算和寿险精算还可以提高保险公司的盈利能力,减少资本的占用。
此外,保险精算和寿险精算还可以为保险公司提供决策支持,帮助保险公司更好地满足客户的需求。
6. 结论保险精算和寿险精算是保险行业中非常重要的一项工作,它们能够帮助保险公司评估和管理保险风险,提高盈利能力,并为保险公司提供决策支持。
因此,保险精算和寿险精算在保险行业中的应用和重要性不可无视。
随着保险业的开展和创新,保险精算和寿险精算在未来将发挥更加重要的作用,为保险行业的可持续开展做出奉献。
第12讲 保险精算

收支相等期间末期的保费收入的本利和(终值)及支付保 险金的本利和(终值)保持平衡来计算; 根据保险合同成立时的保费收入的现值和支付保险金的现 值相等来计算; 根据在某一时点的保费收入和支付保险金的“本利和”或 “现值”相等来计算。
第二节 保险费率的概念
4,882
11,566 23,707 33,598
26.93
18.79 11.98 6.91
90
100 104 105
0.194795
0.386299 0.479911 1
99,580
3,911 438 228
19,398
1,511 210 228
3.66
1.85 1.02 0.50
1990-1993年中国人寿保险业经验生命表(女性)
1,854 1,308 247 494 556 1,177
77.76
76.98 76.12 68.49 58.70 48.98 39.32
50
60 70 80
0.003277
0.009022 0.024610 0.065364
955,337
905,045 779,707 518,795
3,131
8,165 19,189 33,911
纯费率=保额损失率×(1+稳定系数) 保险额损失率=保险赔款总额/总保险金额 ×100%
关键:稳定系数的计算。
保额损失率与保险业务核算中所使用的赔付率指标是两
个不同的概念; 保额损失率是保险赔款与保险金额之比; 赔付率是保险赔款与保费收入之比。
例:某保险公司业务以往七年各年保额损失率按大小排序如 下:(平均保额损失率 M=3‰)
保险精算

保险精算总结20084836 陈徐晟保险精算是依据经济学的基本原理和知识,利用现代数学方法,对各种保险经济活动未来的财务风险进行分性、估价和管理的一门综合性的应用科学。
如研究保险事故的出险规律、保险事故损失额的分布规律、保险人承担风险的平均损失及其分布规律、保险费率和责任准备金、保险公司偿付能力等保险具体问题。
一、保险精算的主要分类1、寿险精算以概率论和数理统计为工具研究人寿保险的寿命分布规律,寿险出险规律,寿险产品的定价,责任准备金的计算,保单现金价值的估值等问题的学科2、非寿险精算是研究除人寿以外的保险标的的出险规律,出险事故损失额度的分布规律,保险人承担风险的平均损失及其分布规律,保费的厘定和责任准备金的提存等问题的学科。
[2]二、保险精算的基本任务保险精算最初的定义是“通过对火灾、盗窃以及人的死亡等损失事故发生的概率进行估算以确定保险公司应该收取多少保费。
”在寿险精算中,利率和死亡率的测算是厘定寿险成本的两个基本问题。
由于利率一般是由国家控制的,所以在相当长的时期里利率并不是保险精算所关注的主要问题,而死亡率的测算即生命表的建立成为寿险精算的核心工作,现在也仍然是精算研究的课题。
非寿险精算始终把损失发生的频率、损失发生的规模以及对损失的控制作为它的研究重心。
现在,非寿险精算已经发展了两个重要分支:一是损失分布理论;二是风险理论。
伴随着金融深化的利率市场化,保险基金的风险也变为精算研究的核心问题。
在这方面要研究的问题包括投资收益的敏感性分析和投资组合分析、资产和负债的匹配等。
[随着统计理论及其不断成熟,保险人在确定保险费率、应付意外损失的准备金、自留限额、未到期责任准备金和未决赔款准备金等方面,都力求采用更精确的方式取代以前的经验判断。
[3]三、保险精算的基本原理保险精算最基本的原理可简单归纳为收支相等原则和大数法则。
[6]所谓收支相等原则就是使保险期内纯保费收入的现金价值与支出保险金的现金价值相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、切比雪夫大数法则
设X1,X2,…,Xn…是由相互独立的随机变
量所构成的序列,每一随机变量都有有限方差,并 且它们有公共上界:
D X 1 C , D X 1 C , D X 1 C , ,
则对于任意的ε>0 ,都有:
ln iP m n 1kn 1Xkn 1kn 1E (Xk) 1
第十二章保险精算
第一节保险精算概述 第二节非寿险精算 第三节寿险精算
第一节保险精算概述
一、保险精算的产生与发展
(一)概念
1、精算:运用数学、统计学、金融理论、保险理 论以及人口学等学科的知识和原理,去解决工作 中的实际问题,进而为决策提供科学依据。
2、保险精算:以概率论和数理统计为基础,是应 用数学、统计学、金融理论、保险理论以及人口 学等学科的知识和原理,去解决商业保险与各种 社会保险业务中需要精确计算的项目。
第二节非寿险精算 一、保险纯费率的确定 保险费率的厘定:是以损失概率为基础的。首先,基于对
保额损失率和均方差的计算求出纯费率;然后,再计算附 加费率。纯费率与附加费率之和即为毛费率。 纯费率:是纯保费占保险金额的比率。依据纯费率计算的 纯保费用于补偿被保险人因保险事故造成保险标的损失。 纯费率的计算公式为:纯费率=保额损失率×(1+稳定系 数)。 纯费率的基本厘订步骤为: (一)选择一组适当的历年保额损失率
管制
C严重通货膨胀导致赔付额大大超过预期 3、精算师:是在保险及其它金融行业、甚
至退休保障等社会福利领域中专司精算职 责的人
精算师的工作范围十分广泛,包括: ① 保险产品的设计:通过对人们保险需求的调查, 设计新的保险条款,而保险条款的设计必须兼顾人 们的不同需要,具有定价的合理性、管理的可行性 以及市场的竞争性; ② 保险费率的计算:根据以往的寿命统计、现行 银行利率和费用率等资料,以确定保单的价格; ③ 准备金和保单现金价值的计算; ④ 调整保费率及保额:根据社会的需要及时间, 调整保费率和保障程度,以增加吸引力和竞争力; ⑤ 审核公司的年底财务报告 ⑥ 投资方向的把握:对公司的各项投资进行评估, 以确保投资的安全和收益; ⑦ 参与公司的发展计划:为公司未来的经济决策 提供有效的数据支持和专业建议。
相等。可以现值或终值相等。 (二)大数法则 在随机现象的大量重复出现中,由于偶然性相互
抵消往往呈现几乎必然的规律,这些定理就是大 数法则。 大数法则是近代保险业赖以建立的数理基础。根 据大数法则的定律,承保的危险单位愈多,损失 概率的偏差愈小,反之,承保的危险单位愈少, 损失概率的偏差愈大。因此,保险人运用大数法 则就可以比较精确地预测危险,合理地厘定保险 费率。
(二)保险精算的产生 1、寿险精算的产生 1)产生之前的寿险发展 寿险的前身基尔特制度:由职业相同者基于互助
精神组成团体,相互救济的制度。该制度起源于欧 洲中世纪,为人寿保险的雏形 1706年伦敦成立协和保险社是最早的资格最老的 寿险组织 1721年成立皇家交易保险公司和伦敦保险公司经 营寿险业务,还有其它机构经营。
二、保险精算的基本任务
按纯费率=损失率要求测算保费 1、寿险
测算利率与死亡率来厘定寿险成本。其中 死亡率即生命表的建立是寿险精算的核心
2、非寿险
把损失发生的频率、规模及对损失的控制 为重点
现代市场利率、保险基金投资风险也成为 研究重点。
三、保险精算的基本原理 (一)收支相等原则 使保险期内纯保费收入与支出保险金的现金价值
2、贝努利大数法则
设 M是n n次贝努利实验中事件A发生的次数,而P 是事件A在每次实验中出现的概率,则对于任意的ε
>0,都有: lim PMn p1
n n
这一法则对于利用统计资料来估计损失概率是极
其重要的。
3、泊松大数法则
假设某一事件在第一次实验中出现的概率为P1,在 第二次实验中出现的概率为P2,…,在第n次实验中
n i1
Xi
(三)在平均保额损失率的基础上附加稳定系数K,确定
纯保险费率
其中, K
X
纯费率X(= 1K)
n
(Xi期望值与实际结果的密切程度,即平均
保额损失率对各实际保额损失率(随机变量各观察值)的代
表程度。稳定系数愈低,则保险经营稳定性愈高;反之,
稳定系数愈高,则保险经营稳定性愈低。对稳定系数低的,
辛普森(Thomas Simpson):根据赫利的生命 表,制作依照死亡率增加而递增的费率表。
陶德森(James Dodson):依据年龄之差等因 素找出计算保费的方法。
逐渐形成了一整套的寿险精算体系。
2、非寿险精算的产生发展 非寿险精算发展相对落后,发展的原因:
A出现了前所未有的巨大风险和新风险 B保险费率大幅下调、奉行客户至上、费率
特点:保费采用赋课制,未将年龄、死亡率等与 保费挂钩,有关计算单一、粗糙,考虑因素少, 缺乏严密的科学基础。
2)寿险精算的产生
荷兰政治家维德(Johan de Witt):倡导一种 终身年金现值计算法,对年金公债的发行提供科 学依据。
英国天文学家赫利(Edmund Halley):在研究 人的死亡率的基础上发明了生命表,使年金计算 更精确
出现的概率为Pn。用M 来n 表示事件在n次实验中发生 的次数,则依据泊松大数法则有:对于任意的ε>0,
下式成立:
ln i P m M n np 1p 2n p n 1
泊松大数法则的意思是说:当实验次数无限增加时
结果所得的比率将无限接近。
大数法则总结:
最有意义的结论是:当保险标的的数量足 够大时,通过以往统计数据计算出来的估 计损失概率与实际概率的误差将很小。
保额损失率是赔偿金额占保险金额的比率。其计算公式为: 保额损失率=赔偿金额/保险金额×100%。
对一组保额损失率的选择标准是: (1)必须有足够的年数; (2)每年的保额损失率须建立在大量统计资料基础之上; (3)选择的每组保额损失率必须是相对稳定的。
(二)计算平均保额损失率
X
1 n
