图论第四章 平面图及着色讲解
图的平面性与图的着色问题
图的平面性与图的着色问题在图论中，图的平面性与图的着色问题是两个重要的研究方向。
图的平面性指的是一种特殊的图的布局方式，使得图的边不相交。
而图的着色问题是指如何给图的顶点进行染色，使得相邻的顶点颜色不相同。
本文将分别介绍图的平面性和图的着色问题，并对其进行详细讨论。
一、图的平面性（Planarity of Graphs）图的平面性是图论中一个经典的问题，研究的是如何将一个图画在平面上，使得图的边不相交。
具体而言，如果一个图可以被画在平面上，且不同边的交点只有顶点，那么我们称该图是一个平面图。
而对于不能在平面上画出来的图，则被称为非平面图。
定理1：一个图是平面图，当且仅当它不包含任何的子图同构于以下两种图之一：K5（五个没有共同边的顶点）或K3,3（六个节点，其中任意两个节点之间都有边相连但不交叉）。
这个定理被称为Kuratowski定理，它为我们判断一个图是否是平面图提供了一个有效的方法。
根据Kuratowski定理，我们可以使用该定理的逆否命题，即如果一个图中包含K5或K3,3，则该图一定是非平面图。
除了Kuratowski定理之外，还有一种判断图的平面性的方法，称为Euler公式。
Euler公式表达了平面图的顶点数、边数和面数之间的关系：V - E + F = 2其中V表示顶点数，E表示边数，F表示面数。
根据Euler公式，对于简单连接图（无环，无孤立点），如果它的顶点数大于等于3且边数大于等于3，且满足Euler公式，则该图是一个平面图。
二、图的着色问题（Graph Coloring）图的着色问题是指如何给一个图的顶点进行染色，使得相邻的顶点颜色不相同。
这里的相邻指的是有边相连的顶点。
在图论中，颜色通常表示为正整数，颜色数则表示为给定图所需的最小颜色数。
对于任意图G，G的最小颜色数被称为G的色数。
如果图G的色数为k，则称图G是可k着色的。
求解一个图的最小色数是一个复杂的问题，称为顶点着色问题（Vertex Coloring Problem），它是一个NP 完全问题。
图的平面图与图的着色
图的平面图与图的着色在图论中，图是由边和顶点组成的数学结构，用来描述事物之间的联系和关系。
图论是一门重要且广泛应用的数学分支，涉及到许多重要的概念和问题，其中包括图的平面图与图的着色。
一、图的平面图在图论中，平面图是指可以被画在平面上而不相交的图。
也就是说，图的边不能相交，且在同一个点上，至多只能有两条边相接。
平面图的研究起源于哥尼斯堡七桥问题。
经过数学家的研究，他们发现了一些重要的结论。
如Euler公式，它是平面图论的基础定理之一。
该定理表明，对于连通的平面图，其顶点数、边数和面数之间存在如下关系：v-e+f=2。
其中v代表顶点数，e代表边数，f代表面数。
除了Euler公式，平面图还有其他一些重要的性质，如四色定理。
四色定理指出，任何一个平面图都可以用不超过四种颜色进行着色，使得任意相邻的两个顶点使用不同的颜色。
二、图的着色图的着色是指给图的每个顶点分配一个颜色，使得相邻的顶点颜色不同。
图的着色问题是图论研究中的一个经典问题，在计算机科学和应用领域有广泛的应用。
在图的着色问题中，有两个重要的概念：色数和色法。
色数是指给图的顶点着色所需使用的最少颜色数目，可以用来衡量图的某种特性。
色法是指给图的所有顶点着色的具体方法。
图的着色问题是一个NP完全问题，也就是说，对于大规模的图，要找到一个最佳的着色方案是非常困难的。
因此，人们通常采用一些启发式算法或者近似算法来解决这个问题。
三、图的平面图与图的着色的应用图的平面图与图的着色在实际生活中有着广泛的应用。
在地图设计中，平面图的概念可以帮助我们设计出不相交的道路、铁路和河流等，使得地图更加直观和易于理解。
在电路设计中，平面图的概念可以帮助我们避免电路中的交叉线，从而简化电路的设计和布线。
在时间表安排中，图的着色可以帮助我们安排不同的任务和活动，使得它们之间没有冲突和重叠。
在频谱分配中，图的着色可以帮助我们将不同的无线电信号分配到不同的频段中，以避免信号之间的干扰。
图论4-6-平面图ppt课件
证明 假设K3,3图是平面图。
在K3,3中任取三个结点，其中必有两个结点不 邻接，故每个面的次数都不小于4， 由4r≤2e，r≤e/2，即 v-e+e/2≥v-e+r=2， v-e/2≥2， 2v- e ≥ 4， 2v4≥e。
在K3,3中有6个结点9条边， 2v-4=2×6-4=8<9,与 2v-4≥e 矛盾， 故 K3,3不是平面图。
整理后得: e≤3v – 6
本定理的用途:判定某图是非平面图。
说明：这是简单 图是平面图的必 要条件。 •图论4-6-平面图
例如：K5中e=10，v=5，3v-6=9，从而e>3v-6， 所以K5不是平面图。
定理4.6.3的条件不是充分的。如K3,3图满 足定理4-6.3的条件（v=6，e=9，3v-6=12， e≤3v-6成立），但K3,3不是平面图。 证明K3,3图不是平面图。
例如图
deg(r1)=3 deg(r2)=3 deg(r3)=5 deg(r4)=4 deg(r5)=3
deg(r1)+deg(r2)+deg(r3)+deg(r4)+deg(r5)
=18
•图论4-6-平面图
3.定理4-6.1 设G为一有限平面图，面的次数之 和等于其边数的两倍。 证明思路：任一条边或者是两个面的共同边界 （贡献2次），或者是一个面的重复边（贡献2次）
•图论4-6-平面图
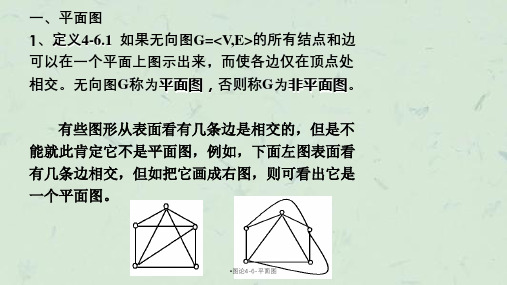
一、平面图 1、定义4-6.1 如果无向图G=<V,E>的所有结点和边 可以在一个平面上图示出来，而使各边仅在顶点处 相交。无向图G称为平面图，否则称G为非平面图。
有些图形从表面看有几条边是相交的，但是不 能就此肯定它不是平面图，例如，下面左图表面看 有几条边相交，但如把它画成右图，则可看出它是 一个平面图。
离散数学中的图的平面图与平面图的着色
图是离散数学中的重要概念，而平面图和平面图的着色是图论中的两个关键概念。
平面图是指在平面上绘制的图形，使得图中的边不会相交。
平面图的着色是指对平面图中的顶点进行染色，且相邻的顶点不会被染成相同的颜色。
平面图的概念最早由欧拉在1736年提出。
他发现，如果一个图是可以在平面上绘制而不会边相交的，那么这个图是一个平面图。
欧拉还引入了一个重要的公式，即欧拉定理，它描述了平面图中的顶点、边和面的关系：V - E + F = 2，其中V代表顶点数，E代表边数，F代表面数。
对于平面图的着色问题，四色定理是一个非常重要的结果。
四色定理指出，任何一个平面图，在不考虑多重边和自环的情况下，最多只需要使用四种颜色就能够对图的顶点进行染色，使得相邻的顶点不会有相同的颜色。
这个定理在1976年被由英国数学家Tomás Oliveira e Silva使用计算机辅助证明，被认为是图论史上的一大突破。
对于平面图的着色，有一种特殊的染色方法叫做四色标号。
四色标号是指对于任意一个平面图，都可以给图中的每个顶点赋予一个自然数，使得相邻的顶点之间的差值不超过3。
这种染色方法保证了相邻的顶点不会被染成相同的颜色，同时最多只需要使用四种颜色。
平面图的着色不仅在图论中有着重要的应用，同时在现实生活中也有很多实际的应用。
比如，考虑地图上的城市，如果我们希望将城市标记成不同的颜色，以表示它们的关系，那么可以利用平面图的着色来实现。
另外，平面图的着色还有很多其他的实际应用，比如在工程规划中用于规划电路的布线、在计算机科学中用于处理图像等等。
总之，离散数学中的图的平面图与平面图的着色是图论中的两个重要概念。
平面图是指在平面上绘制的图形，使得边不会相交；平面图的着色是指对平面图中的顶点进行染色，且相邻的顶点不会被染成相同的颜色。
四色定理是平面图着色的重要结果，它指出任意一个平面图可以使用最多四种颜色进行着色。
平面图的着色在现实生活中有着广泛的应用，是离散数学中的一个重要研究领域。
离散数学 第四章平面图与图【完全免费,强烈推荐】.ppt
f (Tn , t ) t (t 1)n1.
这由 (Tn ) 2即可得证。当 t 2时，f (Tn ,t) 2.
色数与色数多项式
定理 4.6.7
设i,j是G的不相邻结点，则
_
0
—0
f (G, t) f (Gij , t) f (Gij , t). 其中Gij ，Gij 由定义4.6.3给出
d0
，因此
(G' ) d0
1．即
d0
1 种颜
色可以对G '的结点着色，放回结点 vi 恢复成Ｇ，由
于d (vi ) d0 ，所以比有一种与 vi邻点都不同的颜色可
对vi 着色．
色数与色数Байду номын сангаас项式
定理 4.6.3 对于任意一个图G. γ(G) <= 1 + maxδ(G’) 其中δ(G’)是G的导出子图G’中结点的最小度, 极大是对所有的G’而言.
定理 4.5.4 若任何一个3-正则平面图的域可四着色,则任何 一个平面的域也可以四着色.
4.6 色数与色数多项式
定义 4.6.1 给定图G,满足相邻点结点着以不同颜色的最少 颜色数为G的色数,记为γ(G).
定义 4.6.2 给定图G,满足相邻边着以不同颜色的最少颜色 数目称为G的边色数,记为β(G).
色数与色数多项式
定理 4.6.1 一个非空图,γ(G) = 2,当且仅当它没有奇回路.
证明：充分性：在Ｇ中确定一个林 T '，其每个连通子
图都是树Ｔ， (T ) 2．由于每个回路都是偶回路．所
以加入每一条余树边都不会使结点着色发生变化，因
此 (G) 2．
必要性：如果Ｇ中有奇回路，则 (G) 3 ．矛盾．
图论课件--平面图的判定与涉及平面性的不变量共34页文档
46、我们若已接受最坏的，就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会，使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首，不会作诗也会吟。——孙洙 50、谁和我一样用功，谁就会和我一样成功。——莫扎特
图论课件--平面图的判定与涉及平面 性的不变量
6、法律的基础有两个，而且只有两个……公平和实用。——伯克 7、有两种和平的暴力，那就是法律和礼节。——歌德
8、法律就是秩序，有好的法律才有好的秩序。——亚里士多德 9、上帝把法பைடு நூலகம்和公平凑合在一起，可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的，因为好人用不着它们，而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
图论4-4欧拉图和汉PPT课件
此定理是必要条件，可以用来证明一个图不是 汉密尔顿图。
如右图，取S={v1,v4}， 则G-S有3个连通分支，
不满足W(G-S)≤|S|，故 该图不是汉密尔顿图。
说明：此定理是必要条件而不是充分条件。有的图满足此必 要条件，但也是非汉密尔顿图。
所以用此定理来证明某一特定图是非汉密尔顿图并不是 总是有效的。例如，著名的彼得森(Petersen)图，在图中删 去任一个结点或任意两个结点，不能使它不连通；删去3个结 点，最多只能得到有两个连通分支的子图；删去4个结点，只 能得到最多三个连通分支的子图；删去5个或5个以上的结点， 余下子图的结点数都不大于6，故必不能有5个以上的连通分 支数。所以该图满足W(G-S)≤|S|，但是可以证明它是非汉密 尔顿图。
1 1
11 0 1
0
0
0
1
0
1
0
0
10
1d 0c 1b 1a
设有一个八个结点的有向图，如下图所示。其结点分别记为 三位二进制数{000，001，……，111}， 设ai{0,1}，从结点a1 a2 a3可引出两条有向边，其终点分别是a2 a30以及a2 a31。该两条边分别记为a1 a2 a30和a1 a2 a31。 按照上述方法，对于八个结点的有向图共有16条边，在这种图的 任一条路中，其邻接的边必是a1 a2 a3a4和a2 a3a4a5的形式，即是第 一条边标号的后三位数与第二条边的头三位数相同。
4-4 欧拉图
[教学重点] 无向欧拉图的定义、判定定 理和实际应用
[教学难点] 欧拉图判定定理的证明
1、哥尼斯堡七桥问题
哥尼斯堡城有 一条横贯全城 的普雷格尔河， 城的各部分用 七桥联结，每 逢节假日，有 些城市居民进 行环城周游， 于是便产生了 能否“从某地 出发，通过每 桥恰好一次， 在走遍了七桥 后又返回到原 处”的问题。
[理学]图论第四章 平面图及着色
![[理学]图论第四章 平面图及着色](https://img.taocdn.com/s3/m/3a2b5724f12d2af90342e605.png)
v=2,e=1,r=1
v=1,e=1,r=2
(2)下用数学归纳法证明.
假设公式对n条边的图成立.设G有n+1条边. 若G不含圈,任取一点x,从结点x开始沿路行走.因G 不含圈,所以每次沿一边总能达到一个新结点,最后会 达到一个度数为1的结点,不妨设为a,在结点a不能再继 续前进.删除结点a及其关联的边得图G’,G’含有n条边. 由假设公式对G’成立,而G比G’多一个结点和一条边,且 G与G’面数相同,故公式也适合于G. 若G含有圈C,设y是圈C上的一边,则边y一定是两个 不同面的边界的一部分.删除边y得图G’,则G’有n条边. 由假设公式对G’成立而G比G’多一边和多一面,G与G’ 得顶点数相同.故公式也成立.
解:图K5有5个顶点10条边,而3*5-6=9,即10>9,由
推论1知,K5是非平面图. 显然K3,3没有长度为3的圈,且有6个顶点9条边, 因而9>2*6-4,由推论2知K3,3是非平面图. 推论3 设G是带v个顶点，e条边，r个面的平面 图，则 v- e+ r=1+w。其中w为G的连通分支数。 证明:由欧拉公式有: vi- ei+ ri=2(i=1,2,…,w) 从而有 vi- ei+ ri =2w 又 vi=v, ei=e, ri =r+(w-1)(外部面被重 复计算了w-1次.).所以有: V-e+r+(w-1)=2w 整理即得: v- e+ r=1+w.
定理2 对任何平面图G，面的度数之和是边数的二倍。 证明:对内部面而言,因为其任何一条非割边同时在两个 面中,故每增加一条边图的度数必增加2.对外部面的边 界,若某条边不同时在两个面中, 边必为割边,由于边界 是闭链,则该边也为图的度数贡献2.从而结论成立. 定理3 设G是带v个顶点，e条边，r个面的连通的平面 图，则 v-e+r=2。（欧拉公式） 证明:(1)当n=e=1时,如下图,结论显然成立.
图论第4章
例：某博物馆的一层布置如下图，其中边代表走廊，结点 e是入口，结点g是礼品店，通过g我们可以离开博物馆。请找 出从博物馆e进入，经过每个走廊恰好一次，最后从g处离开 的路线。
d j i e b h g c
a
f
21
充分性：已知： (1) G的每条边在W中最多重复一次；
(2) 对于G的每个圈上的边来说，在W中重复的边的总权值 不超过该圈非重复边总权值。
只需证明：任何两条包含G中所有边的闭途径W1与W2, 如果满足定理3的两个条件，则它们有相同的总权值。 设Y1与Y2分别表示W1与W2中重复出现的边集合。 我们先证明：对于任意一个圈C*,如果满足：
eYi E (C* )
w(e)
eE (C* ) Yi
w(e),(i 1, 2)
有：
w(e) w(e)
eY1 eY2
22
Y1与Y2分别表示W1与W2中重复出现的边集合。 令：Y= (Y1-Y2)∪ (Y2-Y1) 断言1：G[Y]的每个顶点度数必然为偶数。 考虑：为何添加Y1或Y2中的边？ 首先，对于G中任意点v, 如果d G (v)是奇数，那么Y1与 Y2中与v关联的边数均为奇数； 如果d G (v)是偶数，那么Y1与Y2中与v关联的边数均为偶数。 其次，设Y1与Y2中与v关联的边数分别为y1与y2, 其中相 同的边数为y0，那么，Y中与v关联的边数为：
(3)
(1) :
令Z1是这个划分的一个圈。若G仅由Z1组成，则G显然是欧拉 图。否则，有另外一个圈Z2与Z1有一个公共点v，从v开始并 且由Z1和Z2相连组成的通道是含有这两个圈中各条边的一条 闭迹。继续这个过程，我们可以构成一条含有G的所有边的 闭迹；从而G是欧拉图。 v2 v4 v1 v5 v3
图论课件-图的顶点着色
AC
所以， (G) 4
7
1
0.5 n 0
0.5
1 2 1.5 t1 0.5 00
1 0.8
0.6 0.4 x 0.2
注：对图的正常顶点着色，带来的是图的顶点集合的
一种划分方式。所以，对应的实际问题也是分类问题。 属于同一种颜色的顶点集合称为一个色组，它们彼此不 相邻接，所以又称为点独立集。用点色数种颜色对图G 正常着色，称为对图G的最优点着色。
若G1是非正则单图，则由数学归纳，G1是可Δ (G)顶点 正常着色的，从而，G是可Δ (G)正常顶点着色的。
(2) 容易证明：若G是1连通单图，最大度是Δ ，则
(G) (G)
15
1
0.5 n 0
0.5
1 2 1.5 t1 0.5 00
1 0.8
0.6 0.4 x 0.2
(3) Δ (G)≥3
11
1
0.5 n 0
0.5
1 2 1.5 t1 0.5 00
1 0.8
0.6 0.4 x 0.2
(1), (v3 )=3
v1
v6
v5
(2),C(v4)=3,C C(v4) 1, 2, 4,5, k 1
(1), (v4 )=1
v2
(2),C(v5)=1,C C(v5) 2,3, 4,5, k 2
v
块
块
块
G -v
17
1
0.5 n 0
0.5
1 2 1.5 t1 0.5 00
1 0.8
0.6 0.4 x 0.2
由于G本身2连通，所以G-xn的每个仅含有一个割点的块 中均有点与xn邻接。设分属于H1与H2中的点x1与x2，它们与 xn邻接。由于x1与x2分属于不同块，所以x1与x2不邻接。又 因为Δ ≥3，所以G-｛x1, x2｝连通。
4 图论
图论维基百科，自由的百科全书跳转到：导航、搜索一个由6个顶点和7条边组成的图图论（Graph theory）是数学的一个分支，它以图为研究对象，研究顶点和边组成的图形的数学理论和方法。
图是区域在头脑和纸面上的反映，图论就是研究区域关系的学科。
区域是一个平面，平面当然是二维的，但是，图在特殊的构造中，可以形成多维（例如大于3维空间）空间，这样，图论已经超越了一般意义上的区域（例如一个有许多洞的曲面，它是多维的，曲面染色已经超出了平面概念）。
图论中的图是由若干给定的顶点及连接两顶点的边所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，用顶点代表事物，用连接两顶点的边表示相应两个事物间具有这种关系。
图论起源于著名的柯尼斯堡七桥问题。
图论的研究对象相当于一维的拓扑学。
目录[隐藏]∙ 1 历史∙ 2 图论问题o 2.1 图的计数o 2.2 子图相关问题o 2.3 染色o 2.4 路径问题o 2.5 网络流与匹配o 2.6 覆盖问题∙ 3 重要的算法∙ 4 参见[编辑]历史柯尼斯堡七桥问题一般认为，于1736年出版的欧拉的关于柯尼斯堡七桥问题的论文是图论领域的第一篇文章。
此问题被推广为著名的欧拉路问题，亦即一笔画问题。
而此论文与范德蒙德的一篇关于骑士周游问题的文章，则是继承了莱布尼茨提出的“位置分析”的方法。
欧拉提出的关于凸多边形顶点数、棱数及面数之间的关系的欧拉公式与图论有密切联系，此后又被柯西等人进一步研究推广，成了拓扑学的起源。
1857年，哈密顿发明了“环游世界游戏”(icosian game)，与此相关的则是另一个广为人知的图论问题“哈密顿路径问题”。
“图”这一名词是西尔维斯特在于1878年发表在《自然》上的一篇论文中提出的。
欧拉的论文发表后一个多世纪，凯莱研究了在微分学中出现的一种数学分析的特殊形式，而这最终将他引向对一种特殊的被称为“树”的图的研究。
由于有机化学中有许多树状结构的分子，这些研究对于理论化学有着重要意义，尤其是其中关于具有某一特定性质的图的计数问题。
图论_6_平图及着色
•
面着色
• 定义1 设e是图G的一条边，如果 ω(G－e)＞ω(G图 4.1
• 定义２ 一个没有割边的连通平图，称为 地图。
• 定义３ 设G是一个地图，对G的每个面着 色，使得没有两个相邻的面着上相同的颜 色，这种着色称为地图的正常面着色 • 地图G可用k种颜色正常面着色，称G是k面 可着色的 • 使得G是k面可着色的数k的最小值称为G的 面色数，记为χ*(G)，若χ*(G)＝k，则称G 是k面色的。
图 论
• 图——基本概念
– 图、路与连通、最短路、有向图、图的矩阵
• Euler图与Hamilton图 • 树
– 树、生成树、有向树
• 平面图 图的着色
– 平面图、对偶图、顶点着色、面着色
• 网络 匹配 独立集
平面图
• 定义1 如果一个图能画在平面上，使得它 的边仅在端点相交，则称这个图为平面图， 或说它是可平面嵌入的，平面图G的这样一 种画法，称为G的一个平面嵌入。 • 平面图G的平面嵌入称为平图。
• 地图的k面可着色问题，可以转化为平面图 的k可着色问题。 • 定理1*(五色定理)任何无自环的平面图G 是5可着色的。 • 证明：对顶点数归纳……
作业
• 证明地图G是２面可着色的，当且仅当它 是一个欧拉图。
• 定理２ 对于任意连通简单图G，有 χ(G)≤1＋△(G)。 • 证明 往证 G是1＋△(G)可着色的。对G的 顶点数施行归纳法， ……
作业
• • 证明 图G是2可着色的，当且仅当G中无 奇圈。 一个图G称为临界的，如果对G的每个真 子图Ｈ，有χ(Ｈ)＜χ(G)。k色的临界图称 为k临界图。证明若G是k临界图，则δ≥k －1。 证明 每个k色图至少有k个度不小于k－1 的顶点。
图论图着色
v4
v5
(b)去掉v0后结点v1与v3处在 同一个连通分支中,v1 与v3有一通路，其中点的颜色红黄交替出现，它与 v0构成一回路C(同一个连通分支)，也就是约当曲线， 这时结点v2处在曲线的内部而结点v5则处在线的外 部，v2与v5的任何连线必与曲线C相交，与平面图的 条件矛盾。因此约当曲线C必然将黑白集中的结点分 成两个连通分支，使v2与v5分别处于两个连通分支中 （也就是v2与v5不连通）， v 于是问题回到(a)，可将v2 v v (或v5)所在的分支中的黑 v 白色对换，于是与v0邻接 v v 的5个结点也只着了4种颜 色， v0就可着第5种颜色。
独立集特点 (1)图G的每一个结点构成一个独立集。 (2)极大独立集不是唯一的，它的基数不一定 是最大的，但它的元素数目已达到极限， 即不可能再加入其他结点而不破坏它的独 立性。 (3)最大独立集必然也是极大独立集而且元素 数目是最多的。 (4)任一完全图Kn的独立数I(Kn)＝1 (5)偶图G只有两个极大独立集，即是它的两 个互补结点子集V1和V2
v1 e1 c1 e3 c3 v3 v0 e2 c2 v2
定理6.4 若G是偶图，则 ψ e (G ) = Δ (最大结点次数) 证：设G的两个互补结点子集为Vl和V2，若|V1|<|V2|，则 在V1中增加一些结点成为V1’使|V1’|=|V2|， 对xi∈V1’及yj∈V2，若G中无边(xi，yj)，则增加一条 边(xi,yj)，通过以上的增添，图G=(V，E)成为图GΔ＝ (V’，E1’)， GΔ 是 Δ次正则偶图，（ 由定理5.4的推论可知）它 有一完美匹配M1，令E2’＝E1’一M1，得到图 G Δ-1＝ (V’，E2’)，则 G Δ-1是(Δ一1)次正则偶图，它也有一 完美匹配M2， 如此继续下去可以得到M1，M2,..., MΔ 个完美匹 配，每一个完美匹配可着一种颜色，使得到G的边 着 色，即 ψ e (G ) = Δ
图论平面图
3
5.1 平面图及其性质
[极大平面图] 设G=(V,E)为简单平面图，|V|3，若对 任意vi ,vjV，且 (vi ,vj) E，有G=(V, E{(vi ,vj)}) 为非平面图，则称G为一个极大平面图。
“极大性”乃针对固定顶点数的图的边的数目而
言。
4
5.1 平面图及其性质
[极大平面图的性质]
个域，则有m=3n-6，d=2n-4。
[证明] 将3d=2m代入欧拉公式。
[推论] 简单平面图G有 m 3n-6，d 2n-4。
[定理5-1-4] 简单平面图至少有一个顶点的度小于6。
[证明] 设任一点的度 6，得 m 3n，矛盾。
6
5.1 平面图及其性质
[二部图] 图G=(V, E)，若V可划分成V1和V2 两部分，
e3
e3
u3
11
5.2 Kuratowski 定理
[同胚] 设无向图 G和G，若存在G，使得G和G分别
经若干串联边置换后与G同构，则称G和G同胚.
与K5同胚的图，称为K(1)型图；与K3,3同胚的图，
称为K(2)型图； K(1)型图和K(2)型图统称K型图。 [定理5-2-1(Kuratowski)] 图 G=(V,E) 可平面当且仅当 G中不存在任何K型子图。( 证略) Kuratowski 定理的实际应用较为困难。
且deg(u2)=2，则称e1与e2串联。
[例 ] e1 u1
u2
e2 u3
10
5.2 Kuratowski 定理
[串联边置换] 将上述e1, e2 置换成 e3=(u1 , u3) ，并消去
可能的多重边的过程，称为串联边置换。
e1 u2 e2 e3
图论第四章(2)
(Ⅶ)
论
4.5 对偶图 1. 定义: 对于给定的平面图G，作相应 的一个图G’：在G的每个域内设置G’的一 个结点；对G中每条边e作G’相应的一条 边e’，联结以e为边界的G的两域中G’的两 个结点。这样得到的G’，称为G的对偶图。
• 对偶图的意义在于，关于域的问题可以 转换成关于结点的问题。 •注意：简单平面图的对偶图是平面图， 但不一定是简单图（可能含重边或环）。
3. 对偶图的应用 定理 每一个平面图G都是5 -可着色的。
证明的思路是作G的对偶图，使问题转化为一 个平面图的点着色问题(相邻点不同色)。因为环 和重边不影响点的着色，故可去掉环和重边，这 样只需要证明一个简单平面图的点5 -可着色即可。 可用数学归纳法证之，具体证明过程略。
经验表明，一张实际的彩色地图使用四种不同颜色即 可区别相邻国家的疆域。“四色猜想”断言，对于任何 一个平面图 (地图)这个结论成立。 四色猜想已由美国数学家阿佩尔与黑肯(1976年)用计 算机程序证明，但尚未找到数学方法给予简练证明。
3)色数多项式
给定图G,如果最多使用t 种颜色对它的结点进行着色, 满足相邻结点着以不同颜色,其着色的不同方案数用f(G,t) 表示。称f(G,t)为G的色数多项式。
• 显然，当t < (G) 时f(G,t)=0；满足f(G,t)>0的最少颜色
数t= (G). • 对平面图G: 五色定理断言 f(G,5)>0， 四色定理断言 f(G,4)>0。
作原图的对偶图(红图)。问题相当于问，其对 偶图中是否存在Euler回路。由于图中有结点度数 为奇，故不存在Euler回路。
例 对平面连通图G的无限域边界上的任意 两结点i和j，求G中分离i和j的所有割集。
离散数学第四篇7图 5-6平面图及图的着色
7-6-2 图中顶点的着色
7-6-3 地图的着色与平面图的点着色 7-6-4 边着色 本章小结 习 题
4
7-5-1 平面图的基本概念
一、关于平面图的一些基本概念 1、 平面图的定义 定义7-5-1 G可嵌入曲面S——如果图G能以这样的方式画在曲面S上 ，即除顶点处外无边相交。 G是可平面图或平面图——若G可嵌入平面。
证明
设G的连通分支分别为G1、G2、…、Gk，并设Gi的顶点数、 边数、面数分别为ni、mi、ri、i=1，2，…，k。
由欧拉公式可知: ni-mi+ri = 2，i=1，2，…，k 易知， m mi，n ni
i 1 i 1 k k
(7-5-1)
由于每个Gi 有一个外部面，而G只有一个外部面，所以G的面数 k r ri k 1
(3)设m＝k(k≥1)时成立，当m＝k+1时，对G进行如下讨论。 若G是树，则G是非平凡的，因而G中至少有两片树叶。 设v为树叶，令G'=G-v，则G'仍然是连通图，且G'的边数 m'=m-1=k，n'=n-1，r'=r。 由假设可知 n'-m'+r'=2，式中n'，m'，r'分别为G'的顶点数， 边数和面数。 于是n-m+r=(n'+1)-(m'+1)+r'=n'-m'+r'=2 若G不是树，则G中含圈。
R1
R0 R2
R3
平面图有4个面，deg(R1)=1,9deg(R2)=3, deg(R3)=2, deg(R0)=8。
定理7-6-1 平面图G中所有面的次数之和等于边数m的两倍，即
图论课件平面图的判定与涉及平面性的不变量
02
平面图的群论性质可以用来研究图的结构和性质，以及图的分
类和识别等问题。
群论在图论中有着广泛的应用，例如在化学分子结构、计算机
03
科学、交通运输等领域中都有重要的应用价值。
05 平面图的算法与复杂性
平面图的算法
欧拉路径与欧拉回路
通过遍历图中的边和顶点，寻找一条路径或回路，满足起点和终点是同一点，且路径或回 路上的所有边和顶点都不重复。
的路径，其中k为正整数。
平面图的边数与顶点数的关系
平面图中顶点数v和 边数e满足：ve+n=1，其中n为平 面的数量。
当平面图为连通图时， 顶点数v和边数e满足： v-e+1>0。
当平面图为简单图时， 顶点数v和边数e满足： v-e+1=0。
平面图的群论性质
01
平面图的群论性质是指平面图在群论中的表现形式，包括对称 性和置换群等。
应用
通过寻找是否存在哈密顿回路来判断一个图是否为平面图。如果存 在哈密顿回路，则该图是平面图。
限制
哈密顿回路判定法不适用于有向图和加权图。
03 平面性的不变量
欧拉路径与欧拉回路
欧拉路径
一个遍历图所有边且每条边只遍 历一次的路径。
欧拉回路
一个遍历图所有边且每条边只遍 历一次，且起点和终点是同一点 的路径。
图的着色问题
给定一个图，使用最少的颜色对图中的顶点进行着色，使得相邻的顶点颜色不同。这是一 个NP完全问题，可以使用贪心算法、回溯算法等求解。
最短路径问题
在图中寻找两个顶点之间的最短路径，可以使用Dijkstra算法、Bellman-Ford算法等求解 。
平面图问题的复杂性
平面图的判定问题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2e=d(f)3r (1)
其中r为G的面数.由欧拉公式 v-e+r=2 所以r=2-v+e,代入(1)中有: 2e3(2-v+e)
即e3v-6。
推论2 设G是带v个顶点，e条边的连通的平面简单图， 其中v3且没有长度为3的圈，则e2v-4。 证明:因为图G中没有长度为3的圈,从而G的每个面的 度数至少为4.因此有2e=d(f)4r (1) 其中r为G的面数.由欧拉公式 v-e+r=2 所以r=2-v+e,代入(1)中有: 2e4(2-v+e) 即e2v-4。
两个点,从交点o到这两点的距离不超过1/2,不妨设为a,x,则点a与x
之间的距离小于1,与已知矛盾,所以G中的边除端点外不再有其它 交点,即G为平面图.再据推论1,知结论成立. a x o
y b
a
x b y
(a)
(b)
第2节 库拉图斯基定理与极大平面
定义1 设G是一个平面图，通过删除G的一条边{x、 y},并增加一个新结点a和两条边{x 、a}与{a、y} （所获得的任何图也是平面图），这样的操作称为 初等细分。若可以从相同的图G通过一系列初等细 分来获得图G1和G2，称G1和G2是同胚的. 如下图G1,G2,G3是同胚的.
G1
G2
G3
定理1一个图G是非平面的，当且仅当它包含一个 同胚于K3.3或K5的子图。（证略）
例1 说明彼得森图不是平面图。 解:删去下图(a)皮得森图的结点b,得其子图(b)H.而 H胚于K3.3,所以皮得森不是平面图.
a f g b a e i c d g h (b)H e h j f d e j f
由推论1,只要证明G为一平面图时即知结论成立. 反设G中存在两条不同的边{a,b}和{x,y}相交于非端点处o,如下
图(a)所示,其夹角为(0< <).
若 =,这时如下图(b),显然存在两点距离小于1,与已知矛盾,从而 0< <.由于a到b的距离为1,x到y的距离为1,因此a,b,x,y中至少有
第四章 平面图
第一节 平面图 定义1 如果图G能画在曲面S上且使得它的边仅在端 点处相交，则称G可嵌入曲面S。如果G可嵌入平面 上，则称G是可平面图，已经嵌入平面上的图 G 称为G的平面表示。
可平面图G与G的平面表示 G 同构，都简称为平面 图。(球极投影)
定理1 图G可嵌入球面图G可嵌入平面。
3
e1 f1 e 4 4 5 f5 e10 2 e7 f3 e6 f2 e8 e9 7
1
f4 e5
e2
e3 6
解:面f1,其边界1e15e24e43e72e101,d(f1)=5. 面f2,其边界1e102e87e91,d(f2)=3. 面f3,其边界2e73e67e82,d(f3)=3. 面f4,其边界3e44e57e63,d(f4)=3. 外部面f5, 其边界1e15e24e36e34 e57e91,d(f5)=6.
例3 K5和K3.3都是非平面图。
解:图K5有5个顶点10条边,而3*5-6=9,即10>9,由
推论1知,K5是非平面图.
显然K3,3没有长度为3的圈,且有6个顶点9条边,因 而9>2*6-4,由推论2知K3,3是非平面图. 推论3 设G是带v个顶点，e条边，r个面的平面图， 则 v- e+ r=1+w。其中w为G的连通分支数。
若G含有圈C,设y是圈C上的一边,则边y一定是两个不 同面的边界的一部分.删除边y得图G’,则G’有n条边.由 假设公式对G’成立，而G比G’多一边和多一面,G与G’ 得顶是带v个顶点，e条边的连通的平面简 单图，其中v3，则e3v-6。 证明:由于G是简单图,则G中无环和无平行边.因此 G的任何面的度数至少为3.故
证明:由欧拉公式有: vi- ei+ ri=2(i=1,2,…,w)
从而有 vi- ei+ ri =2w 又 vi=v, ei=e, ri =r+(w-1)(外部面被重复计算了 w-1次.).所以有: V-e+r+(w-1)=2w
整理即得: v- e+ r=1+w.
推论4 设G是任意平面简单图，则(G)5。
证明:设G有v个顶点e条边.若e6,结论显然成立;若e>6, 假设G的每个顶点的度数6,则由推论1,有
6v 2e 6v-12
矛盾,所以 (G)5.
例4 平面上有n个顶点，其中任意两个点之间的距离 至少为1.证明 在这n个点中距离恰好为1的点对数 至多是3n-6。 证明:首先建立图G=<V,E>,其中V就取平面上给定的n 个点(位置相同),当两个顶点之间的距离为1时,两顶 点之间用一条直线段连接.显然,图G是一个n阶简单 图.
定理2 对任何平面图G，面的度数之和是边数的二倍。
证明:对内部面而言,因为其任何一条非割边同时在两 个面中,故每增加一条边图的度数必增加2.对外部面的 边界,若某条边不同时在两个面中, 边必为割边,由于边 界是闭链,则该边也为图的度数贡献2.从而结论成立.
定理3 设G是带v个顶点，e条边，r个面的连通的平 面图，则 v-e+r=2。（欧拉公式） 证明:(1)当n=e=1时,如下图,结论显然成立.
v=2,e=1,r=1
v=1,e=1,r=2
(2)下用数学归纳法证明.
假设公式对n条边的图成立.设G有n+1条边.若G不 含圈,任取一点x,从结点x开始沿路行走.因G不含圈,所以 每次沿一边总能达到一个新结点,最后会达到一个度数 为1的结点,不妨设为a,在结点a不能再继续前进.删除结 点a及其关联的边得图G’,G’含有n条边.由假设公式对G’ 成立,而G比G’多一个结点和一条边,且G与G’面数相同, 故公式也适合于G.
例1 Q3是否可平面性？
定义2 (平面图的面,边界和度数).
设G是一个平面图，由G中的边所包围的区 域，在区域内既不包含G的结点，也不包含 G的边，这样的区域称为G的一个面。有界 区域称为内部面，无界区域称为外部面。包 围面的长度最短的闭链称为该面的边界。面 的边界的长度称为该面的度数。
例2 指出下图所示平面图的面、面的边界及 面的度数。