2-2-多电子原子的结构

R10 2 1 0.0 0 0 1 2 0.0 0 5 R20 0.5 0.1 R21
3
4
r/a0 0
5
10
r/a0
10
r/a0
径向波函数Rn,l (r ) r图
R30 0.2 0.1 0.0 -0.1 0 10 20 r/a0 0.00 -0.05 0 10 r/a0 R31 0.05 R32 0.04 0.02
最可几半径：最大的极大值所对应的r为最可几半径
n不同，l相同：主量子数小的轨道主峰靠近原子核的内层，所以能量低。 n相同，l不同：虽然主峰位置随l的增大而向核靠近， 但l值越小，峰数目越多，最内层的峰离核最近(钻穿效应)。
径向分布图
思考：两图是否矛盾
径向分布图
比较D(r)和 2(r)
D10, r=a0, 即在半径 a0 处取得极大，而 1s2 则在核附近取得极大。D10与1s2的不同之于不同的物理模型，提出了不同的近似分拆方法。
2.4.1.1 零级近似
忽略电子间的相互作用
n n 1 2 ˆ Z H i 2 i 1 i 1 ri
1 Z 1 Z 1 Z 12 ( 2 2 ) L ( n 2 ) 2 r1 2 r2 2 rn ˆ H i
任意多电子原子Hamilton算符 2.4.1
由于Hamilton算符中含有双原子坐标变量项 e2 4 0 rij ，其薛定谔方程不能精确求解。
多电子原子的Schrö dinger方程及其近似解
采用原子单位制，Schrödinger方程为：
1 N 2 N Z N 1 i E i 1 r i 1 i j r i ij 2 i 1
0 , ;
在 ±z 方向上
角度分布图
例
3 Y px sin cos 4
若作xz平面的剖面图，则 =0
Ypx 3 sin 4
z
若作xy平面剖面图，则 =90
Y px 3 cos 4
y

x

x
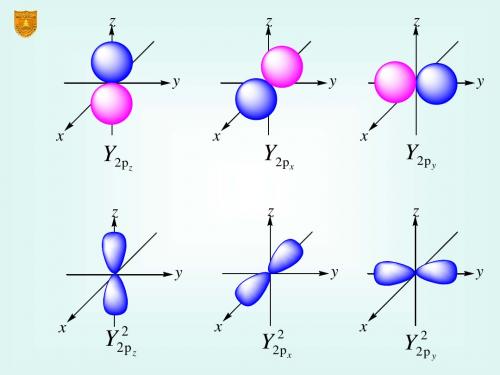
角度分布图
波函数的角度部分图Y ~ (注意标正负)
角度分布图
注意： ( x1, y1, z1, x2 , y2 , z2 ,, xn , y , zn ) (1, 2,, n)
意义： (1, 2, , n) 表示电子1出现在x1 , y1 , z1附近，同时电子2出现在 x2 , y2 , z2附近,的概率密度。
由于rij无法分离(涉及两个电子的坐标)，只能采用近似方法来求解。 求 解 时 首 先 要 将 n 个 电 子 体 系 的 Schrö dinger 方 程 拆 分 成 n 个 单 电 子
0.6 0.5 0.4 0.3 0.2 0.1 0.0 0
处在于它们代表的物理意义不同， 1s2 是
几率密度，而 D10是半径为r处的单位厚度 的球壳内发现电子的几率，在核附近，尽 管 1s2很大，但单位厚度球壳围成的体积 很小，故几率 |1s|2d 自然很小。 r 很大处
D 1s
2
1 2 3 4 5
2 2. 径向密度函数Rn ,l ( r ) r图
表示任意给定角度方向上(即一定 和 )，概率密度 2随r变化情况。 即：
2 2 2 2 Rn ( r ) / R ( r ) ( r , , ) / ,l 1 n ,l 2 1 2 ( r2 , , ) 1
径向分布图
f ( x, y) f1 ( x) f 2 ( y)，单电子近似数学上表示为：f ( x, y) f1 ( x) f 2 ( y)
电子层结构。
2.3 波函数及电子云的图形
nlm (r, , ) Rnl (r)Ylm ( , )
波函数(Ψ，原子轨道)和电子云(|Ψ|2在空间的分布)是三 维空间坐标的函数，将它们用图形表示出来，使抽象的数学 表达式成为具体的图象，对于了解原子的结构和性质，了解 原子化合为分子的过程都具有重要的意义。 Ψ随r的变化关系----径向分布;
意义：
r R (r )dr D(r )dr
2 2 0 0

D(r)：表示半径为r的球面上电子出现的概率密度 D(r)dr：表示半径为r，厚度为dr的球壳内电子出现的概率
径向分布图
2 径向分布函数r 2 Rn ,l (r ) r图
径向分布图
规律
球节面数 n-l-1 极大值数 n-l
2
所反映的仅是角度部分的性质，并非波函数的整体性质。
2.3.3 空间分布图
等值线图
网格立体图
电子云黑点图 原子轨道轮廓图
空间分布图
波函数的等值线图
空间分布图
原子轨道网格图
空间分布图
电子云网格图图
空间分布图
电子云黑点图
球节面数： n - l -1；角节面数：l
空间分布图
例
某类氢原子轨道电子云的角度分布图和径向密度函数图 如下，该轨道式什么轨道，粗略画出其电子云图。
Ylm(,)或 |Ylm(,)|2只与 l,m 有关，而与 n 无关。所以2p, 3p, 4p 的 角度分布却是一样的。因为共价键的方向性主要由 Ylm(,)决定，所以 常以 Ylm(,)代替原子轨道。
角度分布图
电子云的角度分布图 Yl ,m ( , )
2
角节面数=l 角度分布图Yl ,m ( , )和电子云的角度分布图 Yl ,m ( , )
i 1 n
ˆ 1 2 Z) (其中 H i i 2 ri
将一个包含 n 个电子的 Hamilton 拆分成 n 单电子体系 Hamilton ，每 个单电子 Schrö dinger 方程与类氢体系的方程完全一样。第 i 个电子的 Schrö dinger方程方程为：
ˆ (i) E (i) (i) H i i i i
教学目标和要求
第三节 波函数和电子云的图形 掌握 s、p、d原子轨道轮廓图及其特征
第四节 多电子原子的结构
掌握 简单多电子原子体系的Schrödinger方程的表示方法； 简单多电子原子的全波函数表示——Slater行列式。 第五节 元素周期表与元素周期性质 掌握 基态原子核外电子排布原则，第三周期前任一元素的
Dnl(r)的来历
把 2在 , 的全部变化范围积分：

0 0 2 0


2
0
2 (r , , )r 2 sin d d dr

( ) ( ) d ( ) sin d r 2 R 2 ( r )dr
2 0 0


20
0.00 0
10
20
r/a r/a00
径向分布图
2 p (n 2, l 1)
1s (n 1, l 0) 2s (n 2, l 0)
3s (n 3, l 0)
3 p (n 3, l 1)
3d (n 3, l 2)
2 径向密度函数Rn ,l (r ) r图
H原子Hamilton算符
2 2 h e 2 ˆ H 2 8 m 4 0 r
He原子Hamilton算符
多电子原子的Schrö dinger方程及其近似解
原子单位
h 1 au; me 1 au; e 1 au; 4 0 1 au 2
He原子Hamilton算符用原子单位表示为：
z
例
1 Ylm ( , ) Y00 ( , ) 4
为一常数，角度分布为球对称图形。 x
y
角度分布图
例
3 Ypz Y10 ( , ) 10 ( ) 0 ( ) cos 4
3 cos 0 90 4
即xy平面
角向节面
极值
dYpz
3 sin 0 d 4
2.4.2
零级近似
对每一个电子都有(ri,i,i)，(i)称为多电子体系中的单电子波函数，
也即原子轨道。原子轨道(i)对应的能量为：
Z2 E (i) 13.606 2 eV ni
体系的近似波函数
1 2 n i
i 1 n
体系的总能量
E E1 E2 En Ei
径向分布图
2 Rn ,l (r )与Rn ,l ( r ) 的形状只与n和l 有关 2 当半径增加时，Rn ,l (r )与Rn ,l ( r ) 都很快趋于零，离核较远的地方发现
电子的概率非常小。
2 n越大，Rn ,l (r )与Rn ,l ( r )函数图形的伸展范围越大，n决定波函数伸展
范围越大。 n l 1时，会出现Rn ,l (r ) 0的球节面，即在这个球节面上发现电子 的概率密度为零。 球节面的个数：n - l -1
径向分布图
2 3. 径向密度函数r 2 Rn , l ( r ) r图 2 定义：D(r ) r 2 Rn , l ( r )为径向分布函数
Ψ随θ,φ的变化情况称为角度分布;
Ψ随r, θ, φ的变化情况，即空间分布。
2.3.1 径向分布图
径向分布图形
2 2 2 研究：Rn,l (r )、 Rn ( r ) 、 r Rn,l (r ) ,l
1.径向波函数Rn ,l (r ) r图 表示任意给定角度方向上(即一定 和 )，波函数r变化情况。 即： Rn ,l (r1 ) / Rn ,l (r2 ) 1 (r1 , , ) / 2 ( r2 , , )
由Koopman定理预测，He原子的总能量应为： E 79. 0 eV 电子间的排斥能：
79.0 (108.8) 29.8 eV
显然，电子间的排斥能是不能忽略的。虽然零级近似在精度上十分粗糙，但 它启示我们，可以通过一定的近似模型，可以将多电子的拆分成单电子的形式。