最新-初中数学总复习26——图形的相似精品

合集下载

北师大初中数学中考总复习：图形的相似--知识讲解(基础)-推荐.doc

中考总温习：图形的类似 -- 常识解说（根底）【考纲要求】1. 了解线段的比、成份额线段、黄金分割、类似图形有关概念及性质．2. 探究并把握三角形类似的性质及条件，并能使用类似三角形的性质处理简略的实践问题．3. 把握图形位似的概念，能用位似的性质将一个图形扩大或缩小．4. 把握用坐标表明图形的方位与改换，在给定的坐标系中，会依据坐标描出点的方位或由点的方位写出它的坐标，灵活运用不同办法确认物体的方位．【常识网络】类似多边形的特征类似的图形概念1. 界说2. 两角对应持平识别办法3. 两头对应成份额且夹角持平图形的相似相似三角形性质4. 三边对应成份额1. 对应角持平2. 对应边、对应中线、对应角平分线、对应高线、周长的比等于类似比3.面积的比等于相似比的平方使用 : 处理实践问题位似用坐标来确认方位图形与坐标图形的运动与坐标【考点整理】考点一、份额线段1. 份额线段的相关概念假如选用同一长度单位量得两条线段 a，b 的长度分别为 m，n，那么就说这两条线段的比是a bmn，或写成a：b=m：n. 在两条线段的比a：b 中，a 叫做比的前项， b 叫做比的后项.在四条线段中，假如其间两条线段的比等于别的两条线段的比，那么这四条线段叫做成份额线段，简称份额线段 .若四条 a，b，c，d 满意或 a：b=c：d，那么 a，b，c，d 叫做组成份额的项，线段 a，d 叫做份额外项，线段 b，c 叫做份额内项 .如果作为比例内项的是两条相同的线段，即abbc或a：b=b：c，那么线段 b 叫做线段a，c 的比例中项.2、份额的根本性质：①a：b=c：d ad=bc ②a：b=b：c b2 ac .3、黄金分割把线段 AB分红两条线段 AC，BC（AC>BC），并且使 AC是 AB和 BC的份额中项，叫做把线段 AB黄金分割，点C叫做线段AB的黄金分割点，其中AC= 521AB≈0.618AB.考点二、类似图形1. 类似图形：咱们把形状相同的图形叫做类似图形 .也就是说：两个图形相似，其中一个图形可以看作由另一个图形放大或缩小得到的.( 全等是特殊的相似图形).2. 类似多边形：对应角持平，对应边的比持平的两个多边形叫做类似多边形 .3. 类似多边形的性质：类似多边形的对应角持平，对应边成的比持平 .类似多边形的周长的比等于类似比，类似多边形的面积的比等于类似比的平方 .4. 类似三角形的界说：形状相同的三角形是类似三角形 .5. 类似三角形的性质：(1) 相似三角形的对应角相等，对应边的比相等.(2) 相似三角形对应边上的高的比相等，对应边上的中线的比相等，对应角的角平分线的比相等，都等于类似比 .(3) 相似三角形的周长的比等于相似比，面积的比等于相似比的平方.【要害诠释】结合两个图形类似，得出对应角持平，对应边的比持平，这样能够由题中已知条件求得其它角的度数和线段的长.对于复杂的图形，采用将部分需要的图形( 或基本图形) “抽”出来的办法处理.6. 类似三角形的断定：(1) 平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似；(2) 如果两个三角形的三组对应边的比相等，那么这两个三角形相似；(3) 如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似；(4) 如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似.(5) 如果一个直角三角形的斜边和一条直角边与另一个三角形的斜边和一条直角边的比对应相等，那么这两个三角形类似 .考点三、位似图形1. 位似图形的界说：两个多边形不只类似，并且对应极点的连线相交于一点，不通过交点的对应边相互平行，像这样的两个图形叫做位似图形，这个点叫位似中心.2. 位似图形的分类：(1) 外位似：位似中心在连接两个对应点的线段之外.(2) 内位似：位似中心在连接两个对应点的线段上.3. 位似图形的性质位似图形的对应点和位似中心在同一条直线上；位似图形的对应点到位似中心的间隔之比等于类似比；位似图形中不通过位似中心的对应线段平行 .【要害诠释】位似图形是一种特别的类似图形，而类似图形未必能构成位似图形 .4. 作位似图形的过程第一步：在原图上找若干个要害点，并任取一点作为位似中心；第二步：作位似中心与各要害点连线；第三步：在连线上取要害点的对应点，使之满意放缩份额；第四步：依次衔接截取点 .【要害诠释】在平面直角坐标系中，假如位似改换是以原点为位似中心，类似比为k，那么位似图形对应点的坐标的比等于k 或-k.【典型例题】类型一、份额线段1. 在份额尺 1：10 000 000 的地图上，量得甲、乙两个城市之间的间隔是 8 cm，那么甲、乙两个城市之间的实践间隔应为 __________km.【思路指点】地图上的份额尺是一种份额联系，即图上间隔与实践间隔的比 .【答案与解析】 1：10 000 000=8 ：80 000 000 ，即实践间隔是 80 000 000cm=800km.【总结提高】本题考点 : 份额性质 .触类旁通：【变式】如图，为了丈量某棵树的高度，小明用长为 2m的竹竿做丈量东西，移动竹竿，使竹竿、树的顶端的影子刚好落在地上的同一点．此刻，竹竿与这一点相距 6 m、与树相距 15m，则树的高度为______________m【答案】因为，所以树高=7.类型二、类似图形2．如图，一个矩形 ABCD的长 AD=a cm，宽 AB=bcm，E、F 分别是 AD、BC的中点，衔接 E、F，所得新矩形 ABFE与原矩形 ABCD类似，求 a : b 的值．【思路指点】依据类似多边形对应边的比持平，即可求得．12 【答案与解析】∵矩形ABCD的长AD=a ，宽AB=b ，则AE=又矩形AEFB与矩形ABCD相似．12AD=a ．AE AB∴=，AB AD即1ab2b a, 即2 1 2b a2∴a : b 2 :1【总结提高】本题首要考察了类似多边形的对应边的比持平，留意辨明对应边是处理本题的要害．3．如图，△ ABC是一块直角三角形的木块，∠ C=90°，AC=3cm，BC=4cm，AB=5cm，要使用它加工成一块面积最大的正方形木块，问按正方形 CDEF加工仍是按正方形 PQRS加工？说出你的理由 .【思路指点】要加工成一块面积最大的正方形木块，有两种办法，使用类似三角形的断定和性质求出两个正方形的边长，比较巨细即可 .【答案与解析】(1) 如图1，设正方形CDEF的边长为x，则有，得x= cm；(2) 如图2，设正方形PQRS的边长为y，作C N⊥AB于N交RS于M，而知CN= ，同样有得(cm) ，x-y= ＞0，故x＞y，所以按正方形CDEF加工，可得面积最大的正方形.【总结提高】考察类似三角形的使用；用到的常识点为：平行于三角形一边的直线与三角形另两头相交，截得的两三角形类似；类似三角形的对应边成份额；对应高的比等于类似比．触类旁通：【变式】已知矩形 ABCD，长 BC=12cm，宽 AB=8cm，P、Q分别是 AB、BC上运动的两点 . 若 P 自点 A动身，以 1cm/s 的速度沿 AB方向运动，一起， Q自点 B 动身以 2cm/s 的速度沿 BC方向运动，问通过几秒，以P、B、Q为极点的三角形与△ BDC类似？【答案】设经x 秒后，△ PBQ∽△ BCD，因为∠ PBQ=∠BCD= 90°，(1) 当∠1=∠2时，有：，即；(2) 当∠1=∠3时，有：，即∴通过秒或 2 秒，△ PBQ∽△ BCD.4. （2016?闵行区一模）如图，已知在△ABC中AB=AC，点D为BC边的中点，点F 在边AB上，点 E 在线段 DF的延伸线上，且∠ BAE=∠BDF，点 M在线段 DF上，且∠ EBM=∠C．（1）求证：EB? BD=BM? AB；（2）求证：AE⊥BE．【思路指点】（1）依据等腰三角形的性质得到∠ ABC=∠C，由已知条件得到∠ EBM=∠C，等量代换得到∠EBM=∠ABC，求得∠ ABE=∠DBM，推出△ BEA∽△ BDM，依据类似三角形的性质得到，所以得到结论；（ 2）衔接 AD，由等腰三角形的性质得到 AD⊥ BC，推出△ ABD∽△ EBM，依据类似三角形的性质得到∠ ADB=∠EMB=9°0 ，求得∠ AEB=∠BMD=9°0 ，所以得到定论．【答案与解析】证明：（1）∵AB=AC，∴∠ABC=∠C，∵∠EBM=∠C，∴∠EBM=∠ABC，∴∠ABE=∠DBM，∵∠BAE=∠BDF，∴△BEA∽△BDM，∴，∴EB?BD=BM?AB；（ 2）衔接 AD，∵AB=AC，点D为BC边的中点，∴AD⊥BC，∵，∠ABD=∠EBM，∴△ABD∽△EBM，∴∠ADB=∠EMB=9°0，∴∠AEB=∠BMD=90°，∴AE⊥BE．【总结提高】此题考察了类似三角形的断定与性质、勾股定理、等边三角形的断定与性质以及三角函数等常识．此题综合性较强，难度较大，解题的要害是精确作出辅助线，把握转化思维与数形结合思维的使用．5．（2015?丽水）如图，在矩形ABCD中，E为CD的中点，F为BE上的一点，连结CF并延长交AB于点M，MN⊥CM交射线AD于点N．（1）当F为BE中点时，求证：AM=C；E（2）若==2，求的值；（3）若==n，当n为何值时，MN∥BE？【思路指点】（1）如图1，易证△ BMF≌△ ECF，则有 BM=EC，然后依据 E为CD的中点及 AB=DC就可得到AM=EC；（ 2）如图2，设MB=a，易证△ ECF∽△ BMF，依据类似三角形的性质可得 EC=2a，由此可得 AB=4a，AM=3a，BC=AD=2a．易证△ AMN∽△ BCM，依据类似三角形的性质即可得到 AN= a，然后可得 ND=AD﹣AN= a，就可求出的值；（ 3）如图3，设MB=a，同（ 2）可得 BC=2a，CE=na．由 MN∥BE，MN⊥MC可得∠ EFC=∠HMC=9°0 ，然后可证到△ MBC∽△ BCE，然后依据类似三角形的性质即可求出 n 的值．【答案与解析】解：（1）当F为BE中点时，如图1，则有BF=EF．∵四边形ABCD是矩形，∴AB=DC，AB∥DC，∴∠MBF=∠CEF，∠BMF=∠ECF．在△BMF和△ECF中，，∴△BMF≌△ECF，∴BM=E．C∵E为C D的中点，∴EC=DC，∴BM=EC=DC=AB，∴AM=BM=E；C（2）如图2，设MB=a，∵四边形ABCD是矩形，∴AD=BC，AB=DC，∠A=∠ABC=∠BCD=9°0，AB∥D C，∴△ECF∽△BMF，∴==2，∴EC=2a，∴AB=CD=2CE=4，a AM=AB﹣MB=3a．∵=2，∴BC=AD=2．a∵MN⊥MC，∴∠CMN=9°0 ，∴∠AMN∠+ BMC=9°0 ．∵∠A=90°，∴∠ANM∠+ AMN=9°0 ，∴∠BMC∠= ANM，∴△AMN∽△BCM，∴= ，∴= ，∴AN= a，ND=AD﹣AN=2a﹣a= a，∴= =3；（3）当= =n时，如图3，设MB=a，同（2）可得BC=2a，CE=na．∵MN∥BE，MN⊥MC，∴∠EFC=∠HMC=9°0 ，∴∠FCB+∠FBC=90°．∵∠MBC=9°0 ，∴∠BMC∠+ FCB=90°，∴∠BMC∠= FBC．∵∠MBC∠= BCE=90°，∴△MBC∽△BCE，∴= ，∴= ，∴n=4．【总结提高】本题首要考察了类似三角形的断定与性质、全等三角形的断定与性质、矩形的性质、同角的余角持平、三角形外角的性质等常识，使用类似三角形的性质得到线段之间的联系是处理本题的要害．类型三、位似图形y A16 . 如图，已知图中的每个小方格都是边长为1 的小正109方形，每个小正方形的极点称为格点．若△ ABC与△A 1B1C1 是位8似图形，且极点都在格点上，则位似中心的坐标是 ___________．76 A54B1 C132B C11 2 3 4 5 6 7 8 9 10 11 x【思路指点】衔接恣意两对对应点，看连线的交点为那一点即为位似中心．【答案与解析】衔接 BB1，A1A，易得交点为（ 9，0）．【总结提高】用到的常识点为：位似中心为位似图形上恣意两对对应点连线的交点．触类旁通：【变式】下列图形中不是位似图形的是( ).【答案】 C.。

八年级数学下《图形的相似》专题复习课件

相似多边形概念：各角对应相等、各边对应成比例的两个多边形叫
做相似多边形。
相似比概念：相似多边形对应边的比叫做相似比。
注:1、相似符号“∽ ”读作“相似于”
2、在记两个多边形相似时，要把表示对应角顶点的字母写在对应的位置上。
相似多边形性质：
相似多边形的对应角相等，对应边成比例相似多边形的周长之比等于相似比相似多边形的面积之比等于相似比的平方
这样的两个多边形叫做位似多边形，点 O叫做位似中心。
结论
在直角坐标系中，将一个多边形每个顶点的横、纵坐标都乘以同一个数k （k≠0），所对应的图形与原图形位似，位似中心是坐标原点，他们的相似比为∣k∣.
【典例精讲1】
如图所示，在梯形ABCD中， AD∥ BC， EF∥ BC，且将梯形 ABCD分成两个相似的梯形 AEFD和梯形 EBCF，若 AD＝ 3 ， BC＝ 4 ，则 EF的长为________．
解析梯形AEFD、EBCF相似，AE与EB是相似梯形的对应边，根据相似多边形的对应边相等，因而可以把求AE：EB转化为求AD：EF．
解：梯形AEFD∽梯形EBCF， ∴AD:EF=EF:BC 又∵AD=3，BC=4， ∴EF²=AD•BC=3×4=12， ∵EF＞0，
∴EF= 2 3
总结：本题考查了相似多边形的对应边的比相等．
黄金分割定义
点C把线段AB分成两条线段AC和BC，如果 AC BC ，那么称线段AB被点C
AB AC
黄金分割，点C叫做线段AB的黄金分割点，AC与AB的比叫做黄金比.
知识呈现
如果两个相似多边形每组对应点所在的直线都经过同一个点O，且每组对应点与O 点的距离之比都等于一个
定值k，例如OA′=k·OA（k≠0），那么

中考复习-图形的相似共22页PPT资料

7
常见相似模型？
7. 如图，由边长为1的25个小正方形组成的
正方形网格上有一个ΔABC.
( 1 )在网格上画出一个与ΔABC相似且面积
最正方大形的的ΔA顶1B点1C上1,使. 它的三个顶点都落在小CC1
(2) ΔA1B1C1的
5 面积是________.
A
B A B1
1.如图所示,把ΔABC沿AB边平移到ΔA'
(2)合分比性质:如果 badc，那a_b么 _b_ c_d._d _
(3)等比性质:
如果 acm(bdn0)， bd n
那_a么 b_cd_ __m n____.ba_. __
3.相似三角形:填写下表
相似三角形定义 _对__应__角__相等,_对__应__边__成比例的三角形.
的影长A‘B’与金字塔的影长AB,即可近似算
பைடு நூலகம்
出金字塔的高度OB.
O
O'
A
B A' B'
如果O'B'=1,A'B'=2,AB=274,求金字塔的高度OB.
O O'
A
B A' B'
4.将两块完全相同的等腰直角三角板摆成如
图的样子,假设图中的所有点、线都在同一
平面内,那么图形中有相似(不包括全等)三角
判 (1)_两__角__对__应__相__等__;__________. 定 (2)两__边__对__应__成__比__例__且__夹__角__相__等__.
(3)__三__边__对__应__成__比__例____________. 性 (1)_对__应__角__相等;面积比=相似比的平方质 (2)对应线段对__应__边__,_对__应__中__线_,_对__应__高___,

新初中数学图形的相似知识点总复习附答案解析(2)

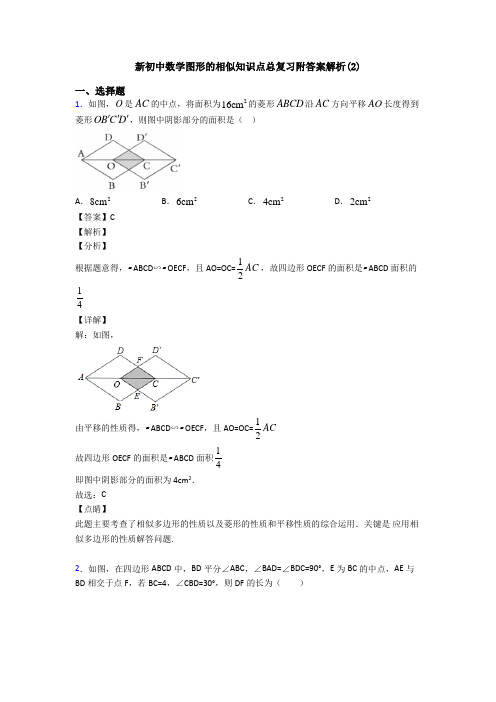
新初中数学图形的相似知识点总复习附答案解析(2)一、选择题1．如图，O 是AC 的中点，将面积为216cm 的菱形ABCD 沿AC 方向平移AO 长度得到菱形OB C D '''，则图中阴影部分的面积是（）A ．28cmB ．26cmC ．24cmD ．22cm【答案】C【解析】【分析】根据题意得，▱ABCD ∽▱OECF ，且AO=OC=12AC ，故四边形OECF 的面积是▱ABCD 面积的14【详解】解：如图，由平移的性质得，▱ABCD ∽▱OECF ，且AO=OC=12AC 故四边形OECF 的面积是▱ABCD 面积14即图中阴影部分的面积为4cm 2．故选：C【点睛】此题主要考查了相似多边形的性质以及菱形的性质和平移性质的综合运用．关键是应用相似多边形的性质解答问题.2．如图，在四边形ABCD 中，BD 平分∠ABC ，∠BAD=∠BDC=90°，E 为BC 的中点，AE 与BD 相交于点F ，若BC=4，∠CBD=30°，则DF 的长为（）A．235B．233C．334D．435【答案】D【解析】【分析】先利用含30度角的直角三角形的性质求出BD，再利用直角三角形的性质求出DE=BE=2，即：∠BDE=∠ABD，进而判断出DE∥AB，再求出AB=3，即可得出结论．【详解】如图，在Rt△BDC中，BC=4，∠DBC=30°，∴3连接DE，∵∠BDC=90°，点D是BC中点，∴DE=BE=CE=12BC=2，∵∠DCB=30°，∴∠BDE=∠DBC=30°，∵BD平分∠ABC，∴∠ABD=∠DBC，∴∠ABD=∠BDE，∴DE∥AB，∴△DEF∽△BAF，∴DF DE BF AB＝，在Rt△ABD中，∠ABD=30°，3，∴AB=3，∴23 DFBF＝，∴25 DFBD＝，∴DF=224323555BD =⨯=，故选D ．【点睛】此题主要考查了含30度角的直角三角形的性质，相似三角形的判定和性质，角平分线的定义，判断出DE ∥是解本题的关键．3．如图，四边形ABCD 内接于O e ，AB 为直径，AD CD =，过点D 作DE AB ⊥于点E ，连接AC 交DE 于点F .若3sin 5CAB ∠=，5DF =，则AB 的长为( )A ．10B ．12C ．16D ．20【答案】D【解析】【分析】连接BD ，如图，先利用圆周角定理证明ADE DAC ∠=∠得到5FD FA ==，再根据正弦的定义计算出3EF =，则4AE =，8DE =，接着证明ADE DBE ∆∆∽，利用相似比得到16BE =，所以20AB =．【详解】解：连接BD ，如图，AB Q 为直径，90ADB ACB ∴∠=∠=︒，AD CD =Q ，DAC DCA ∴∠=∠，而DCA ABD ∠=∠，DAC ABD ∴∠=∠，DE AB ∵⊥，90ABD BDE ∴∠+∠=︒，而90ADE BDE ∠+∠=︒，ABD ADE ∴∠=∠，ADE DAC ∴∠=∠，5FD FA ∴==，在Rt AEF ∆中，3sin 5EF CAB AF ∠==Q ， 3EF ∴=， 22534AE ∴=-=，538DE =+=，ADE DBE ∠=∠Q ，AED BED ∠=∠，ADE DBE ∴∆∆∽，::DE BE AE DE ∴=，即8:4:8BE =，16BE ∴=，41620AB ∴=+=．故选：D ．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90︒的圆周角所对的弦是直径．也考查了解直角三角形．4．如图，在ABC V 中，点D ，E 分别为AB ，AC 边上的点，且//DE BC ，CD 、BE 相较于点O ，连接AO 并延长交DE 于点G ，交BC 边于点F ，则下列结论中一定正确的是( )A ．AD AE AB EC= B ．AG AE GF BD = C ．OD AE OC AC = D ．AG AC AF EC = 【答案】C【解析】【分析】由//DE BC 可得到DEO V ∽CBO V ，依据平行线分线段成比例定理和相似三角形的性质进行判断即可．【详解】解：A.∵//DE BC ，∴AD AE AB AC= ,故不正确； B. ∵//DE BC ，∴AG AE GF EC = ,故不正确； C. ∵//DE BC ，∴ADE V ∽ABC V ，DEO V ∽CBO V ,DE AE BC AC ∴=，DE OD BC OC = ． OD AE OC AC∴= ，故正确； D. ∵//DE BC ，∴AG AE AF AC= ,故不正确；故选C ．【点睛】本题主要考查的是相似三角形的判定和性质，熟练掌握相似三角形的性质和判定定理是解题的关键．5．如图，点E 是ABCD Y 的边AD 上一点，2DE AE =，连接BE ，交AC 边于点F ，下列结论中错误的是（）A ．3BC AE =B ．4AC AF = C ．3BF EF =D ．2BC DE =【答案】D【解析】【分析】由平行四边形的性质和相似三角形的性质分别判断即可．【详解】解：∵在ABCD Y 中，//AD BC ，AD BC =，∴AEF CBF V :V ,∴AE AF EF CB CF BF==, ∵2DE AE = ∴332BC DE AE ==，选项A 正确，选项D 错误， ∴133AF AE AE CF CB AE ===，即：3CF AF =， ∴4AC AF =，∴选项B 正确，∴133EF AE AE BF CB AE ===，即：3BF EF =， ∴选项C 正确，故选：D ．【点睛】此题主要考查了平行四边形的性质以及相似三角形的判定与性质，能熟练利用相似三角形对应边成比例是解题关键．6．如图，正方形OABC 的边长为6，D 为AB 中点，OB 交CD 于点Q ，Q 是y ＝k x上一点，k 的值是（）A ．4B ．8C ．16D ．24【答案】C【解析】【分析】延长根据相似三角形得到:1:2BQ OQ =，再过点Q 作垂线，利用相似三角形的性质求出QF 、OF ，进而确定点Q 的坐标，确定k 的值．【详解】解：过点Q 作QF OA ⊥，垂足为F ，OABC Q 是正方形，6OA AB BC OC ∴====，90ABC OAB DAE ∠=∠=︒=∠，D Q 是AB 的中点，12BD AB ∴=， //BD OC Q ，OCQ BDQ ∴∆∆∽，∴12 BQ BD OQ OC==，又//QF ABQ，OFQ OAB∴∆∆∽，∴22213QF OF OQAB OA OB====+，6AB=Q，2643QF∴=⨯=，2643OF=⨯=，(4,4)Q∴，Q点Q在反比例函数的图象上，4416k∴=⨯=，故选：C．【点睛】本题考查了待定系数法求反比例函数、相似三角形的性质和判定，利用相似三角形性质求出点Q的坐标是解决问题的关键．7．如图，将ABC∆沿BC边上的中线AD平移到A B C'''∆的位置．已知ABC∆的面积为16，阴影部分三角形的面积9．若1AA'=，则A D'等于（）A．2 B．3 C．4 D．32【答案】B【解析】【分析】由S△ABC＝16、S△A′EF＝9且AD为BC边的中线知1922A DE A EFS S'∆'∆==，182ABD ABCS S∆∆==，根据△DA′E∽△DAB知2A DEABDSA DAD S∆∆'⎛⎫='⎪⎝⎭，据此求解可得．【详解】16ABCS∆=Q、9A EFS∆'=，且AD为BC边的中线，1922A DE A EF S S ∆∆''∴==，182ABD ABC S S ∆∆==， Q 将ABC ∆沿BC 边上的中线AD 平移得到A B C '''∆，//A E AB ∴'， DA E DAB '∴∆~∆，则2A DE ABD S A D AD S ∆∆'⎛⎫=' ⎪⎝⎭，即22991816A D A D ⎛⎫== '⎪+⎝⎭'，解得3A D '=或37A D '=-（舍），故选：B ．【点睛】本题主要平移的性质，解题的关键是熟练掌握平移变换的性质与三角形中线的性质、相似三角形的判定与性质等知识点．8．在Rt △ABC 中，∠BAC ＝90°，AD 是△ABC 的中线，∠ADC ＝45°，把△ADC 沿AD 对折，使点C 落在C ′的位置，C ′D 交AB 于点Q ，则BQ AQ的值为（） ABCD【答案】A【解析】【分析】根据折叠得到对应线段相等，对应角相等，根据直角三角形的斜边中线等于斜边一半，可得出AD ＝DC ＝BD ，AC ＝AC′，∠ADC ＝∠ADC ′＝45°，CD ＝C′D ，进而求出∠C 、∠B 的度数，求出其他角的度数，可得AQ ＝AC ，将BQ AQ 转化为BQ AC ，再由相似三角形和等腰直角三角形的边角关系得出答案．【详解】解：如图，过点A 作AE ⊥BC ，垂足为E ，∵∠ADC ＝45°，∴△ADE 是等腰直角三角形，即AE ＝DE＝2AD ，在Rt △ABC 中，∵∠BAC ＝90°，AD 是△ABC 的中线，∴AD ＝CD ＝BD ，由折叠得：AC ＝AC ′，∠ADC ＝∠ADC ′＝45°，CD ＝C ′D ，∴∠CDC ′＝45°+45°＝90°，∴∠DAC ＝∠DCA ＝（180°﹣45°）÷2＝67.5°＝∠C ′AD ，∴∠B＝90°﹣∠C＝∠CAE＝22.5°，∠BQD＝90°﹣∠B＝∠C′QA＝67.5°，∴AC′＝AQ＝AC，由△AEC∽△BDQ得：BQAC＝BDAE，∴BQAQ＝BQAC＝ADAE＝2AEAE＝2．故选：A．【点睛】考查直角三角形的性质，折叠轴对称的性质，以及等腰三角形与相似三角形的性质和判定等知识，合理的转化是解决问题的关键．9．如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，如果AC=3，AB=6，那么AD的值为（）A．32B．92C33D．3【答案】A【解析】【分析】【详解】解：∵Rt△ABC中，∠ACB=90°，CD⊥AB于点D，∴△ACD∽△ABC，∴AC：AB=AD：AC，∵AC=3，AB=6，∴AD=32．故选A．考点：相似三角形的判定与性质．10．如图，已知在平面直角坐标系中，点O 是坐标原点，AOB V 是直角三角形，90AOB ∠=︒，2OB OA =，点B 在反比例函数2y x =上，若点A 在反比例函数k y x=上，则k 的值为( )A ．12B ．12-C ．14D ．14- 【答案】B【解析】【分析】通过添加辅助线构造出相似三角形，再根据相似三角形的性质可求得1,2x A x ⎛⎫- ⎪⎝⎭，然后由点的坐标即可求得答案．【详解】解：过点B 作BE x ⊥于点E ，过点A 作AF x ⊥于点F ，如图：∵点B 在反比例函数2y x=上 ∴设2,B x x ⎛⎫ ⎪⎝⎭∴OE x =，2BE x =∵90AOB ∠=︒∴90AOD BOD ∠+∠=︒∴90BOE AOF ∠+∠=︒∵BE x ⊥，AF x ⊥∴90BEO OFA ∠=∠=︒∴90OAF AOF ∠+∠=︒∴BOE OAF ∠=∠∴BOE OAF V V ∽∵2OB OA = ∴12OF AF OA BE OE BO ===∴121122OF BE x x =⋅=⋅=，11222x AF OE x =⋅=⋅= ∴1,2x A x ⎛⎫- ⎪⎝⎭∵点A 在反比例函数k y x=上 ∴12x k x=- ∴12k =-．故选：B【点睛】本题考查了反比例函数与相似三角形的综合应用，点在函数图象上则点的坐标就满足函数解析式，结合已知条件能根据相似三角形的性质求得点A 的坐标是解决问题的关键．11．如图，Rt ABC V 中，90,60ABC C ∠=∠=o o ，边AB 在x 轴上，以O 为位似中心，作111A B C △与ABC V 位似，若()3,6C 的对应点()11,2C ，则1B 的坐标为（）A ．()1,0B ．3,02⎛⎫ ⎪⎝⎭C ．()2,0D ．()2,1【答案】A【解析】如图，根据位似图形的性质可得B 1C 1//BC ，点B 在x 轴上，由∠ABC=90°，可得B 1C 1⊥x 轴，根据C 1坐标即可得B 1坐标．【详解】如图，∵111A B C △与ABC V 位似，位似中心为点O ，边AB 在x 轴上，∴B 1C 1//BC ，点B 在x 轴上，∵∠ABC=90°，∴B 1C 1⊥x 轴，∵C 1坐标为（1，2），∴B 1坐标为（1，0）故选：A ．【点睛】本题考查位似图形的性质，位似图形的对应边互相平行，对应点的连线相交于一点，这一点叫做位似中心．12．在平面直角坐标系中，已知点E （﹣4，2），F （﹣2，﹣2），以原点O 为位似中心，相似比为，把△EFO 缩小，则点E 的对应点E′的坐标是A ．（﹣2，1）B ．（﹣8，4）C ．（﹣8，4）或（8，﹣4）D ．（﹣2，1）或（2，﹣1）【答案】D【解析】试题分析：根据位似的性质，缩小后的点在原点的同侧，为（-2,1），然后求在另一侧为（2，-1）．故选D考点：位似变换13．在相同时刻，物高与影长成正比，如果高为1米的标杆影长为2米，那么影长为30米的旗杆的高为（）A ．20米B ．18米C ．16米D ．15米【答案】D【解析】在同一时刻物高和影长成正比，即在同一时刻的两个物体，影子，经过物体顶部的太阳光线三者构成的两个直角三角形相似，利用标杆的高：标杆影长=旗杆的高：旗杆的影长，列出方程，求解即可得出旗杆的高度．【详解】解：根据题意解：标杆的高：标杆影长=旗杆的高：旗杆的影长，即1:2=旗杆高：30，∴旗杆的高=130=152⨯米．故选：D．【点睛】本题主要考察的是相似三角形的应用，正确列出方程是解决本题的关键．14．如图，菱形ABCD中，点P是CD的中点，∠BCD=60°，射线AP交BC的延长线于点E，射线BP交DE于点K，点O是线段BK的中点，作BM⊥AE于点M，作KN⊥AE于点N，连结MO、NO，以下四个结论：①△OMN是等腰三角形；②tan∠OMN=3；③BP=4PK；④PM•PA=3PD2，其中正确的是（）A．①②③B．①②④C．①③④D．②③④【答案】B【解析】【分析】根据菱形的性质得到AD∥BC，根据平行线的性质得到对应角相等，根据全等三角形的判定定理△ADP≌△ECP，由相似三角形的性质得到AD=CE，作PI∥CE交DE于I，根据点P是CD的中点证明CE=2PI，BE=4PI，根据相似三角形的性质得到1=4KP PIKB BE=，得到BP=3PK，故③错误；作OG⊥AE于G，根据平行线等分线段定理得到MG=NG，又OG⊥MN，证明△MON是等腰三角形，故①正确；根据直角三角形的性质和锐角三角函数求出∠OMN=33，故②正确；然后根据射影定理和三角函数即可得到PM•PA=3PD2，故④正确．【详解】解：作PI∥CE交DE于I，∵四边形ABCD为菱形，∴∠DAP=∠CEP ，∠ADP=∠ECP ，在△ADP 和△ECP 中，DAP CEP ADP ECP DP CP ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ADP ≌△ECP ，∴AD=CE ，则PI PD CE DC =，又点P 是CD 的中点， ∴1=2PI CE ， ∵AD=CE ， ∴1=4KP PI KB BE =， ∴BP=3PK ，故③错误；作OG ⊥AE 于G ， ∵BM 丄AE 于M ，KN 丄AE 于N ，∴BM ∥OG ∥KN ，∵点O 是线段BK 的中点，∴MG=NG ，又OG ⊥MN ，∴OM=ON ，即△MON 是等腰三角形，故①正确；由题意得，△BPC ，△AMB ，△ABP 为直角三角形，设BC=2，则CP=1，由勾股定理得，则根据三角形面积公式，BM=7， ∵点O 是线段BK 的中点，∴PB=3PO ，∴OG=13BM=21， MG=23MP=27， tan ∠OMN=OG MG ，故②正确； ∵∠ABP=90°，BM ⊥AP ，∴PB 2=PM•PA ，∵∠BCD=60°，∴∠ABC=120°，∴∠PBC=30°，∴∠BPC=90°，∴PB=3PC ，∵PD=PC ，∴PB 2=3PD ，∴PM •PA=3PD 2，故④正确．故选B ．【点睛】本题考查相似形综合题．15．已知线段MN ＝4cm ，P 是线段MN 的黄金分割点，MP ＞NP ，那么线段MP 的长度等于（）A ．（5）cmB ．（5﹣2）cmC 5）cmD 51）cm 【答案】B【解析】【分析】根据黄金分割的定义进行作答.【详解】由黄金分割的定义知，51MP MN -=MN=4，所以，5- 2. 所以答案选B. 【点睛】本题考查了黄金分割的定义，熟练掌握黄金分割的定义是本题解题关键.16．如图，矩形AEHC 是由三个全等矩形拼成的，AH 与BE 、BF 、DF 、DG 、CG 分别交于点P 、Q 、K 、M 、N ，设BPQ ∆，DKM ∆，CNH ∆的面积依次为1S 、2S 、3S ，若1320S S +=，则2S 的值为( )A ．6B ．8C ．10D ．1【答案】B【解析】【分析】由已知条件可以得到△BPQ ∽△DKM ∽△CNH ，然后得到△BPQ 与△DKM 的相似比为12，△BPQ 与△CNH 的相似比为13，由相似三角形的性质求出1S ，从而求出2S . 【详解】解：∵矩形AEHC 是由三个全等矩形拼成的，∴AB=BD=CD ，AE ∥BF ∥DG ∥CH ，∴四边形BEFD 、四边形DFGC 是平行四边形，∠BQP=∠DMK=∠CHN ，∴BE ∥DF ∥CG ，∴∠BPQ=∠DKM=∠CNH ，∴△ABQ ∽△ADM ，△ABQ ∽△ACH ， ∴12AB BQ AD DM ==，13BQ AB CH AC ==， ∴△BPQ ∽△DKM ∽△CNH ， ∵12BQ MD =，13BQ CH =， ∴1214S S =，1319S S =， ∴214S S =，319S S =，∵1320S S +=，∴12S =，∴2148S S ==；故选：B.【点睛】本题考查了相似三角形的判定和性质，矩形的性质以及平行四边形的判定和性质，解题的关键是熟练掌握相似三角形的判定和性质，正确得到214S S =，319S S =，从而求出答案.17．若△ABC 的每条边长增加各自的50%得△A 'B 'C '，若△ABC 的面积为4，则△A 'B 'C '的面积A ．9B ．6C ．5D ．2 【答案】A【解析】【分析】根据两个三角形三边对应成比例，这两个三角形相似判断出两个三角形相似，根据相似三角形的性质即可得到结论．【详解】解：∵△ABC 的每条边长增加各自的50%得△A ′B ′C ′，∴△ABC 与△A ′B ′C ′的三边对应成比例，∴△ABC ∽△A ′B ′C ′， ∴214()150%9ABC A B C S S '''==+V V ， ∵△ABC 的面积为4，则△A'B'C'的面积是9．故选：A ．【点睛】本题考查了相似三角形的性质和判定，熟练掌握相似三角形的判定是解题的关键．18．两个相似三角形的对应边分别是15cm 和23cm ，它们的周长相差40cm ，则这两个三角形的周长分别是（）A ．45cm ，85cmB ．60cm ，100cmC ．75cm ，115cmD ．85cm ，125cm 【答案】C【解析】【分析】根据相似三角形的周长的比等于相似比列出方程，解方程即可．【详解】设小三角形的周长为xcm ，则大三角形的周长为（x+40）cm ，由题意得，154023x x =+，解得，x=75，则x+40=115，故选C ．19．如图，点D 是ABC V 的边BC 上一点，,2BAD C AC AD ∠=∠= ，如果ACD V 的面积为15，那么ABC V 的面积为（）A ．20B ．22.5C ．25D ．30【解析】【分析】先证明C ABD BA ∽△△，再根据相似比求出ABC V 的面积即可．【详解】∵,BAD C B B ∠=∠=∠∠∴C ABD BA ∽△△∵2AC AD =∴4S ABD S CBA =V V ∴43S ACD S CBA =V V ∵ACD V 的面积为15∴44152033S CBA S ACD ==⨯=VV 故答案为：A ．【点睛】本题考查了相似三角形的问题，掌握相似三角形的性质以及判定定理是解题的关键．20．如图，在Rt ABC △中，90ACB ∠=︒，CD AB ⊥于点D ，2CD =，1BD =，则AD 的长是（）A ．1.B 2C ．2D ．4【答案】D【解析】【分析】由在Rt △ABC 中，∠ACB=90°，CD ⊥AB ，根据同角的余角相等，可得∠ACD=∠B ，又由∠CDB=∠ACB=90°，可证得△ACD ∽△CBD ，然后利用相似三角形的对应边成比例，即可求得答案．【详解】∵在Rt △ABC 中,∠ACB=90°，CD ⊥AB ，∴∠CDB=∠ACB=90°，∴∠ACD+∠BCD=90°,∠BCD+∠B=90°，∴∠ACD=∠B ，∴△ACD ∽△CBD ，∴=AD CD CD BD， ∵CD=2，BD=1， ∴2=21AD ， ∴AD=4.故选D.【点睛】此题考查相似三角形的判定与性质，解题关键在于证得△ACD ∽△CBD.。

八年级数学下册第十章《图形的相似》复习课件

BC=16cm，点P从A点开始沿AB边
向点B以2cm/s的速度移动，点Q从
点B开始沿BC边向点C以4cm/s的速
度移动。若点P、Q从A、B处同时
出发，经过几秒钟后，⊿PBQ与
⊿ABC相似？
B
Q
P
A
C
•11、凡为教者必期于达到不须教。对人以诚信，人不欺我;对事以诚信，事无不成。 •12、首先是教师品格的陶冶，行为的教育，然后才是专门知识和技能的训练。 •13、在教师手里操着幼年人的命运，便操着民族和人类的命运。2022/1/172022/1/17January 17, 2022 •14、孩子在快乐的时候，他学习任何东西都比较容易。 •15、纪律是集体的面貌，集体的声音，集体的动作，集体的表情，集体的信念。 •16、一个人所受的教育超过了自己的智力，这样的人才有学问。 •17、好奇是儿童的原始本性，感知会使儿童心灵升华，为其为了探究事物藏下本源。2022年1月2022/1/172022/1/172022/1/171/17/2022 •18、人自身有一种力量，用许多方式按照本人意愿控制和影响这种力量，一旦他这样做，就会影响到对他的教育和对他发生作用的环境。 2022/1/172022/1/17
第十章图形的相似
（复习课）
一、相似的图形相似三角形的性质
二、相似三角形相似三角形的识别
三、位似三角形
对应边成比例，对应角相等
对应高，对应中线，对应角平分线的比等于相似比对应周长的比等于相似比对应面积的比等于相似比的平方
一个三角形的两角与另一个三角形的两角对应相等
一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等
P
∠B＝∠ACP或∠ACB＝∠APC或

初中数学专题复习图形的相似（含答案）

初中数学专题复习图形的相似（含答案）第19课时图形的相似一、知识导航图应用:解决实际问题3.面积的比等于相似比的平方2.对应边、对应中线、对应角平分线、对应高线、周长的比等于相似比1.对应角相等4.三边对应成比例3.两边对应成比例且夹角相等2.两角对应相等1.定义图形的运动与坐标用坐标来确定位置位似性质识别方法相似多边形的特征概念图形与坐标相似三角形相似的图形图形的相似二、中考课标要求三、中考知识梳理1.比例线段由于比例线段的实质就是四个正数组成的比例式,所以要学好本部分内容,首先要复习小学所学的有关比例的相关知识.2.相似形具有相同形状的图(大小不一定相同). 3.相似多边形的特征“对应边成比例,对应角相等”既是相似多边形的识别方法又是性质. 4.相似比相似比是把一个图形放大或缩小的倍数,其具有顺序性,全等是相似比为 1 时的特殊情况.5.相似三角形的性质(1)对应边成比例,对应角相等;(2)对应高的比、对应中线的比、对应角平分线的比都等于相似比;(3)周长的比等于相似比,面积的比等于相似比的平方. 6.相似图形的画法是新课标中新增添的内容,要求掌握用多种方法将一个图形放大或缩小. 7.图形与坐标是新课程中新增添的内容,应注意把“形”与“数”紧密地联系在一起. 四、中考题型例析1.列比例式例1 (2002·北京怀柔)已知三个数请你再添上一个(只填一个)数, 使它们能构成一个比例式,则这个数是_________.分析:这是一道开放型试题,由于题中没有告知构成比例的各数顺序, 故应考虑各种可能位置.答案2.相似三角形的识别例2 (2004·昆明)如图,在△ABC 中,AC>AB,点D 在AC 边上(点D 不与A 、C 重合),若再增加上条件就能使△ABD ∽△ACB,则这个条件可以是_______.解析:由于所识别的两三角形隐含着一个公共角∠A,因此依照识别方法,只要再附加条件∠ABD=∠C,∠ADB=∠ABC,或AD ABAB AC =即可. 答案:∠ABD=∠C,∠ADB=∠ABC,AD ABAB AC=。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

（26）图形的相似
〖考试内容〗
比例的基本性质，线段的比，成比例线段.图形的相似及性质.三角形相似的条件，图形的位似.
〖考试要求〗
①了解比例的基本性质，了解线段的比、成比例线段，通过实例了解黄金分割.
②通过实例认识图形的相似，了解相似图形的性质.知道相似多边形的对应角相等，对应边成比例，面
积的比等于对应边比的平方.
③了解两个三角形相似的概念，掌握两个三角形相似的条件.
④了解图形的位似，能够利用位似将一个图形放大或缩小.
⑤通过实例了解物体的相似，利用图形的相似解决一些实际问题（如利用相似测量旗杆的高度）.
〖考点复习〗
1．比例的基本性质

[例1]．（2018丽水）已知52ab，则abb=＿＿＿＿＿。
2．成比例的线段
[例2]．（2018南京）7．在比例尺为1：40000的工程示意图上，将于2018年9月1日正式通车的南京地
铁一号线（奥体中心至迈皋桥段）的长度约为54.3cm,它的实际长度约为（）
A、0.2172km B、2.172km
C、21.72km D、217.2km
3．相似图形的性质
[例3]．（2018资阳）在△ABC中，若D、E分别是边AB、AC上的点，且DE∥BC，AD=1，
DB=2，则△ADE与△ABC的面积比为____________.
4．相似三角形的判定
[例4]．（2018深圳）如图9，D、E分别是△ABC的边AC、AB上的点，请你添加一个条
件，使△ADE与△ABC相似．你添加的条件是
[例5]．（2018枣庄）如图，小正方形的边长均为1，则下列图中的三角形(阴影部分)与△ABC
相似的是( )

[例6]．（2018湟中）如图，有一块三角形土地，它的底边BC=100米，高AH=80米，
某单位要沿着地边BC修一座底面是矩形DEFG的大楼，D、G分别在边AB、AC上.
若大楼的宽是40米，求这个矩形的面积.
〖考题训练〗
1．（2018宁波）如果ab ＝23 ，那么aa＋b ＝＿＿＿＿＿。

3．（2018陕西）应中共中央总书记胡锦涛同志的邀请，中国国民党主席连战先生亲民
党主席宋楚瑜先生分别从台湾来大陆参观访问，先后来到西安，都参观了新建筑的“大唐芙蓉园”，该园
占地面积约为80 0000ｍ2，若按比例尺1∶2000缩小后，其面积大约相当于（）
A. 一个篮球场的面积
B. 一张乒乓球台台面的面积
C. 《陕西日报》的一个版面的面积

A
B
C
D
E

图9

D
A
B
C

H E G F
D. 《数学》课本封面的面积
4．（2018沈阳）如图，已知△ACP∽△ABC，AC = 4，AP = 2，则AB的长为 .

5．（2018芜湖）如图，已知CD是Rt△ABC的斜边上的高，其中AD=9cm，BD=4cm，
那么CD等于_______cm.
6．（2018厦门）已知：如图2，在△ABC中，∠ADE＝∠C，则下列等式成立的是（）
A. ADAB＝AEAC

B. AEBC＝ADBD
C. DEBC＝AEAB
D. DEBC＝ADAB
7．（2018 内江市）如图，P是Rt△ABC的斜边BC上异于B，C的一点，过P点作直线截
△ABC，使截得的三角形与△ABC相似，满足这样
条件的直线共有（）条。

A、1 B、2 C、3 D、4
8．(2018潍坊)如图,△ABC中，D为AC上一点，CD＝2DA,∠BAC=45°,
∠BDC=60°,CEBD,E为垂足,连接AE.
(1)写出图中所有相等的线段,并加以证明;
(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由;
(3)求△BEC与△BEA的面积之比.
〖课后作业〗

①．（2018温州）若ab＝35 ，则a＋bb的值是( )

A、85 B、35 C、32 D、58
③．（2018南京）如果两个相似三角形对应高的比是1：2，那么它们的面积比
是。
④．（2018海口）如图，D、E两点分别在AC、AB上，且DE与BC不平行，请
填上一个你认为合适的条件：，使得△ADE∽△ABC.
⑤．（2018上海）在△ABC中，点D、E分别在边AB和AC上，且DE∥BC，如果AD＝2，DB＝4，AE
＝3，那么EC＝
⑥．（2018上海）在下列命题中，真命题是（）
A、两个钝角三角形一定相似 B、两个等腰三角形一定相似
C、两个直角三角形一定相似 D、两个等边三角形一定相似
⑦．（2018厦门）矩形ABCD中,M是BC边上且与B、C不重合的点,点P是射线AM上的点,若以A、P、
D为顶点的三角形与△ABM相似,则这样的点有个.

（2018资阳）6. 如图2，若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点，为使△ABC∽△PQR，
则点R应是甲、乙、丙、丁四点中的
A. 甲 B. 乙 C. 丙 D. 丁

D
B
A
C

E
D
C B

A
C

P
B

A
B
D
C
E

A
D
B

C
⑧．（2018桂林）已知矩形ABCD中，AB＝2，BC＝3，F是CD的中点，一束光线从A点出发，通过BC

边反射，恰好落在F点（如图），那么，反射点E与C点的距离为＿＿＿＿＿＿。

B
D

C
E