振动理论作业答案y-作业
燕山大学振动理论习题答案

=l/2,l3=l/4,不计钢杆质量。试求系统的无阻尼固有频率n 及阻尼 。
图 2-9 {2.26} 图 T 2-26 所示的系统中,m = 1 kg,k = 144 N / m,c = 48 N•s / m,l1 = l = 0.49
m,l2 = 0.5 l, l3 = 0.25 l,不计刚杆质量,求无阻尼固有频率n 及阻尼 。
解:图(1)为系统的静平衡位置,以 为系统的广义坐标,画受力如图(2)
I 2l c (2l ) 3l k( 3l) 3lP0 sint
又 I=ml2
4c m
k m
3 ml
P0
sin t
则
p
2 n
9k m
2n
4c m
,
h 3p0 ml
B
h ( pn2 2 )2 (2n)2
根据:
Tmax Vmax, xmax n xmax
n2
k2 m1
k1
R12 R22
I R22
3 2 m2
2-8 如图 2-8 所示的系统中,钢杆质量不计,建立系统的运动微分方程,并求临 界阻尼
系数及阻尼固有频率。
图 2-8
a
ca
b
kb
ml
l
解:
ml l ca a kb b 0 ml2 ca2 kb2 0
(2)若将支撑突然撤去,质量块又将下落多少距离?
{2.17} 图 T 2-17 所示的系统中,四个弹簧均未受力,k1= k2= k3= k4= k,试问: (1)若将支承缓慢撤去,质量块将下落多少距离? (2)若将支承突然撤去,质量块又将下落多少距离?
k1
k2
k3
m
k4
解:
机械振动第二三四次作业参考答案

θ
由题意可得,质心的速度为:
v ( R r )
又由于圆盘的速度等于质心的速度,故有
v盘 v ( R r )
故有: 则系统的动能为:
盘
v盘 R r r r
Ek
1 2 1 2 1 1 1 Rr 2 2 2 mv J盘 mR - r ( mr 2 )( ) 2 2 2 2 2 r
cx kx p(t ) m x
带入数据后可得,该系统运动方程为:
400 x 17000 x 240 sin 3t 0 275 x
(2)由(1)可知,系统的固有频率为:
n
系统的阻尼比为:
k 17000 7.862rad / s m 275
2
1 . 1 9 9 4 1m 0
h tan 1
故有:
2 1 2 0.0925 1.199 tan 2.67 rad 2 2 1 1 1.199
xu hu pu 1.199 104 240 0.0288 m
因此,系统的稳态响应为:
I 0 a k1 a l k2 l 0
整理可得,系统运动方程为: 1 2 ml (a 2 k1 l 2 k2 ) 0 3 (2)由系统运动微分方程,求固有频率:
n
keq meq
a 2 k1 l 2 k2
3(a 2 k1 l 2 k2 ) 1 2 ml 3 ml 2
对于激励 p2 (t ) ,求其阻尼比
2
p 2 0.7992 n 7.862
2
对应的频响函数的幅值和相位角分别为:
hu 2
1 1 k (1 22 )2 (22 )2 1 1 17000 (1 0.79922 )2 (2 0.0925 0.7992) 2
振动理论课后答案

解:
模态函数的一般形式为:
题设边界条件为:
,
边界条件可化作:
,
导出C2= 0及频率方程:
,其中
解:
,
不计质量的梁上有三个集中质量,如图所示。用邓克利法计算横向振动的基频。
图
解:
当系统中三个集中质量分别单独存在时:
, ,
在图所示系统中,已知m和k。用瑞利法计算系统的基频。
图
解:
近似选取假设模态为:
系统的质量阵和刚度阵分别为:
,
由瑞利商公式:
在图所示系统中,已知k和J。用传递矩阵法计算系统的固有频率和模态。
解:
设该简谐振动的方程为 ; 二式平方和为
将数据代入上式:
;
联立求解得
A=10.69cm; 1/s;T= s
当 时, 取最大,即:
得:
答:振动周期为;振幅为10.69cm;最大速度为22.63m/s。
1-3一个机器内某零件的振动规律为 ,x的单位是cm, 1/s。这个振动是否为简谐振动试求它的振幅、最大速度及最大加速度,并用旋转矢量表示这三者之间的关系。
求图T 2-7中系统的固有频率,悬臂梁端点的刚度分别是 及 ,悬臂梁的质量忽略不计。
图T 2-7答案图T 2-7
解:
和 为串联,等效刚度为: 。(因为总变形为求和)
和 为并联(因为 的变形等于 的变形),则:
和 为串联(因为总变形为求和),故:
故:
由一对带偏心质量的等速反向旋转齿轮构成的振动机械安装在弹簧和阻尼器构成的支承上,如图所示。当齿轮转动角速度为 时,偏心质量惯性力在垂直方向大小为 。已知偏心重W=N,偏心距e=15.0cm,支承弹簧总刚度系数k=N/cm,测得垂直方向共振振幅 ,远离共振时垂直振幅趋近常值 。求支承阻尼器的阻尼比及在 运行时机器的垂直振幅。
东北大学物理作业答案振动和波

第9章 振动 作 业一、教材:选择填空题 1~5;计算题:13,14,18 二、附加题(一)、选择题1、一沿x 轴作简谐振动的弹簧振子,振幅为A ,周期为T ,振动方程用余弦函数表示,如果该振子的初相为π34,则t =0时,质点的位置在: D(A )过A x 21=处,向负方向运动; (B) 过A x 21=处,向正方向运动; (C) 过A x 21-=处,向负方向运动; (D) 过A x 21-=处,向正方向运动。
2、一物体作简谐振动,振动方程为:x =A cos(?t +?/4 )在t=T/4(T 为周期)时刻,物体的加速度为: B(A) 222ωA -. (B) 222ωA . (C) 232ωA -. (D)232ωA . (二)、计算题1、一物体沿x 轴做简谐运动,振幅A = 0.12m ,周期T = 2s .当t = 0时, 物体的位移x 0= 0.06m ,且向x 轴正向运动.求: (1)此简谐运动的运动方程;(2)t = T /4时物体的位置、速度和加速度; 解:(1)0.12cos 3x t ππ⎛⎫=- ⎪⎝⎭m(2)0.12sin 3v t πππ⎛⎫=-- ⎪⎝⎭m/s 20.12cos 3a t πππ⎛⎫=-- ⎪⎝⎭m/s 2 t = T /4时0.12cos 0.106x π==≈m0.12sin 0.060.196v πππ=-=-≈- m/s20.12cos 0.06 1.026a πππ=-=-≈- m/s 22、一物体沿x 轴做简谐运动,振幅A = 10.0cm ,周期T = .当t = 0时, 物体的位移x 0= -5cm ,且向x 轴负方向运动.求: (1)简谐运动方程; (2)t = 时,物体的位移;(3)何时物体第一次运动到x = 5cm 处(4)再经过多少时间物体第二次运动到x = 5cm 处 解:(1)20.1cos 3x t ππ⎛⎫=+ ⎪⎝⎭m(2)t = 时,270.1cos 0.1cos 0.087236x πππ⎛⎫=+=≈- ⎪⎝⎭m (3)利用旋转矢量法,第一次运动到x = 5cm 处,相位是15233t πππ=+所以 11t =s(3)利用旋转矢量法,第二次运动到x = 5cm 处,相位是27233t πππ=+所以 253t =s 215210.6733t t t s ∆=-=-==3、若简谐振动方程为m ]4/20cos[1.0ππ+=t x ,求: (1)振幅、频率、角频率、周期和初相;(2)t =2s 时的位移、速度和加速度. 解:(1)可用比较法求解.据]4/20cos[1.0]cos[ππϕω+=+=t t A x得:振幅0.1A m =,角频率20/rad s ωπ=,频率1/210s νωπ-==, 周期1/0.1T s ν==,/4rad ϕπ=(2)2t s =时,振动相位为:20/4(40/4)t rad ϕππππ=+=+ 据cos x A ϕ=,sin A νωϕ=-,22cos a A x ωϕω=-=-得 20.0707, 4.44/,279/x m m s a m s ν==-=-4、一简谐振动的振动曲线如图所示,求振动方程. 解:设所求方程为)cos(ϕω+=t A x当t=0时:115,0x cm v =-<由A 旋转矢量图可得:02/3t rad ϕπ== 当t=2s 时:从x-t 图中可以看出:220,0x v => 据旋转矢量图可以看出, 223/2t rad ϕπππ==-+=题图4所以,2秒内相位的改变量203/22/35/6t t rad ϕϕϕπππ==∆=-=-= 据t ϕω∆=∆可求出:/5/12/t rad s ωϕπ=∆∆=于是:所求振动方程为:520.1cos()()123x t SI ππ=+5、一物体沿x 轴作简谐振动,振幅为0.06m ,周期为,当t =0时位移为0.03m ,且向轴正方向运动,求:(1)t =时,物体的位移、速度和加速度;(2)物体从m 03.0-x =处向x 轴负方向运动开始,到达平衡位置,至少需要多少时间解:设该物体的振动方程为)cos(ϕω+=t A x 依题意知:2//,0.06T rad s A m ωππ=== 据Ax 01cos -±=ϕ得)(3/rad πϕ±= 由于00v >,应取)(3/rad πϕ-= 可得:)3/cos(06.0ππ-=t x(1)0.5t s =时,振动相位为:/3/6t rad ϕπππ=-= 据22cos ,sin ,cos x A v A a A x ϕωϕωϕω==-=-=- 得20.052,0.094/,0.512/x m v m s a m s ==-=-(2)由A 旋转矢量图可知,物体从0.03x m =-m 处向x 轴负方向运动,到达平衡位置时,A 矢量转过的角度为5/6ϕπ∆=,该过程所需时间为:/0.833t s ϕω∆=∆=第10章 波动 作 业一、教材:选择填空题 1~5;计算题:12,13,14, 21,30 二、附加题(一)、选择题1、一平面简谐波的波动方程为y = (3?t -?x+?) (SI). t = 0时的波形曲线如图所示,则: C(A) O 点的振幅为-0.1m . (B) 波长为3m . (C) a 、b 两点间相位差为?/2 . (D) 波速为9m/s .2、某平面简谐波在t = 时波形如图所示,则该波的波函数为: A(A) y = [4? (t -x /8)-?/2] (cm) . (B) y = [4? (t + x /8) + ?/2] (cm) . (C) y = [4? (t + x /8)-?/2] (cm) .(D) y = [4? (t -x /8) + ?/2] (cm) .3、一平面简谐波在0 t 时刻的波形曲线如图所示?,则O 点的振动初位相为: D题图5ux (m)y (m) · ··O -· a b4cmOy (cm) x (cm)t = u =8cm/sπππ23)(;)(;21)(;0)(D C B A4、一平面简谐波?,其振幅为A ?,频率为v ?,波沿x 轴正方向传播?,设t t =0时刻波形如图所示?,则x=0处质点振动方程为:B;])(2cos[)(;]2)(2cos[)(];2)(2cos[)(;]2)(2cos[)(0000ππππππππ+-=--=+-=++=t t v A y D t t v A y C t t v A y B t t v A y A5、关于产生驻波的条件,以下说法正确的是: D (A) 任何两列波叠加都会产生驻波; (B) 任何两列相干波叠加都能产生驻波; (C) 两列振幅相同的相干波叠加能产生驻波;(D) 两列振幅相同,在同一直线上沿相反方向传播的相干波叠加才能产生驻波. (二) 计算题1、如图所示?,一平面简谐波沿Ox 轴传播?,波动方程为])(2cos[ϕλπ+-=xvt A y ?,求:1)P 处质点的振动方程; 2)该质点的速度表达式与加速度表达式?。
作业————振动作业及答案

第五章作业5-1 写出本章你觉得重要旳知识点。
5-2质量为kg 10103-⨯旳小球与轻弹簧构成旳系统,按)SI ()328cos(1.0ππ+=x 旳规律作谐振动,求:(1)振动旳周期、振幅和初位相及速度与加速度旳最大值; (2)最大旳答复力、振动能量、平均动能和平均势能,在哪些位置上动能与势能相等? (3)s 52=t 与s 11=t 两个时刻旳位相差;解:(1)设谐振动旳原则方程为)cos(0φω+=t A x ,则知:3/2,s 412,8,m 1.00πφωππω===∴==T A 又 πω8.0==A v m 1s m -⋅ 51.2=1s m -⋅2.632==A a m ω2s m -⋅(2) N 63.0==m m a FJ 1016.32122-⨯==m mv E J 1058.1212-⨯===E E E k p当p k E E =时,有p E E 2=,即)21(212122kA kx ⋅=∴ m 20222±=±=A x (3) ππωφ32)15(8)(12=-=-=∆t t 5-3一种沿x 轴作简谐振动旳弹簧振子,振幅为A ,周期为T ,其振动方程用余弦函数表达.如果0=t 时质点旳状态分别是:(1)A x -=0;(2)过平衡位置向正向运动; (3)过2Ax =处向负向运动; (4)过2A x -=处向正向运动.试求出相应旳初位相,并写出振动方程.解:由于 ⎩⎨⎧-==0000sin cos φωφA v A x将以上初值条件代入上式,使两式同步成立之值即为该条件下旳初位相.故有)2cos(1πππφ+==t T A x)232cos(232πππφ+==t T A x)32cos(33πππφ+==t T A x)452cos(454πππφ+==t T A x5-4一质点同步参与两个在同始终线上旳简谐振动,振动方程为⎪⎩⎪⎨⎧-=+=m)652cos(3.0m )62cos(4.021ππt x t x 试分别用旋转矢量法和振动合成法求合振动旳振动幅和初相,并写出谐振方程。
大学物理学振动与波动习题答案

大学物理学(上)第四,第五章习题答案第4章振动P174.4.1 一物体沿x轴做简谐振动,振幅A = 0.12m,周期T = 2s.当t = 0时,物体的位移x = 0.06m,且向x轴正向运动.求:(1)此简谐振动的表达式;(2)t = T/4时物体的位置、速度和加速度;(3)物体从x = -0.06m,向x轴负方向运动第一次回到平衡位置所需的时间.[解答](1)设物体的简谐振动方程为x = A cos(ωt + φ),其中A = 0.12m,角频率ω = 2π/T= π.当t = 0时,x = 0.06m,所以cosφ = 0.5,因此φ= ±π/3.物体的速度为v = d x/d t = -ωA sin(ωt + φ).当t = 0时,v = -ωA sinφ,由于v > 0,所以sinφ < 0,因此φ = -π/3.简谐振动的表达式为x= 0.12cos(πt –π/3).(2)当t = T/4时物体的位置为x= 0.12cos(π/2–π/3)= 0.12cosπ/6 = 0.104(m).速度为v = -πA sin(π/2–π/3)= -0.12πsinπ/6 = -0.188(m·s-1).加速度为a = d v/d t = -ω2A cos(ωt + φ)= -π2A cos(πt - π/3)= -0.12π2cosπ/6 = -1.03(m·s-2).(3)方法一:求时间差.当x = -0.06m 时,可得cos(πt1 - π/3) = -0.5,因此πt1 - π/3 = ±2π/3.由于物体向x轴负方向运动,即v< 0,所以sin(πt1 - π/3) > 0,因此πt1 - π/3 = 2π/3,得t1 = 1s.当物体从x= -0.06m处第一次回到平衡位置时,x = 0,v > 0,因此cos(πt2 - π/3) = 0,可得πt2 - π/3 = -π/2或3π/2等.由于t2 > 0,所以πt2 - π/3 = 3π/2,可得t2 = 11/6 = 1.83(s).所需要的时间为Δt = t2 - t1 = 0.83(s).方法二:反向运动.物体从x = -0.06m,向x轴负方向运动第一次回到平衡位置所需的时间就是它从x= 0.06m,即从起点向x 轴正方向运动第一次回到平衡位置所需的时间.在平衡位置时,x = 0,v < 0,因此cos(πt - π/3) = 0,可得πt - π/3 = π/2,解得t = 5/6 = 0.83(s).[注意]根据振动方程x = A cos(ωt + φ),当t = 0时,可得φ = ±arccos(x0/A),(-π < φ≦π),初位相的取值由速度决定.由于v = d x/d t = -ωA sin(ωt + φ),当t = 0时,v = -ωA sinφ,当v > 0时,sinφ < 0,因此φ = -arccos(x0/A);当v < 0时,sinφ > 0,因此φ = arccos(x0/A).可见:当速度大于零时,初位相取负值;当速度小于零时,初位相取正值.如果速度等于零,当初位置x0 = A时,φ = 0;当初位置x0 = -A时,φ= π.4.2 已知一简谐振子的振动曲线如图所示,试由图求:(1)a,b,c,d,e各点的位相,及到达这些状态的时刻t各是多少?已知周期为T;(2)振动表达式;(3)画出旋转矢量图.[解答]方法一:由位相求时间.(1)设曲线方程为x = A cosΦ,其中A表示振幅,Φ = ωt + φ表示相位.由于x a = A,所以cosΦa = 1,因此Φa = 0.由于x b = A/2,所以cosΦb = 0.5,因此Φb = ±π/3;由于位相Φ随时间t增加,b点位相就应该大于a点的位相,因此Φb = π/3.由于x c = 0,所以cosΦc = 0,又由于c点位相大于b位相,因此Φc = π/2.同理可得其他两点位相为Φd = 2π/3,Φe = π.c点和a点的相位之差为π/2,时间之差为T/4,而b点和a点的相位之差为π/3,时间之差应该为T/6.因为b点的位移值与O时刻的位移值相同,所以到达a点的时刻为t a = T/6.到达b点的时刻为t b = 2t a = T/3.到达c点的时刻为t c = t a + T/4 = 5T/12.到达d点的时刻为t d = t c + T/12 = T/2.到达e点的时刻为t e = t a + T/2 = 2T/3.(2)设振动表达式为x = A cos(ωt + φ),当t = 0时,x = A/2时,所以cosφ = 0.5,因此φ =±π/3;由于零时刻的位相小于a点的位相,所以φ = -π/3,因此振动表达式为cos(2)3tx ATπ=π-.另外,在O时刻的曲线上作一切线,由于速度是位置对时间的变化率,所以切线代表速度的方向;由于其斜率大于零,所以速度大于零,因此初位相取负值,从而可得运动方程.(3)如图旋转矢量图所示.方法二:由时间求位相.将曲线反方向延长与t轴相交于f点,由于x f= 0,根据运动方程,可得cos(2)03tTππ-=图6.2所以232f t Tπππ-=±. 显然f 点的速度大于零,所以取负值,解得 t f = -T /12.从f 点到达a 点经过的时间为T /4,所以到达a 点的时刻为t a = T /4 + t f = T /6,其位相为203a a t T Φπ=π-=. 由图可以确定其他点的时刻,同理可得各点的位相.4.3如图所示,质量为10g 的子弹以速度v = 103m·s -1水平射入木块,并陷入木块中,使弹簧压缩而作简谐振动.设弹簧的倔强系数k= 8×103N·m -1,木块的质量为4.99kg ,不计桌面摩擦,试求:(1)振动的振幅; (2)振动方程.[解答](1)子弹射入木块时,由于时间很短,木块还来不及运动,弹簧没有被压缩,它们的动量守恒,即mv = (m + M )v 0.解得子弹射入后的速度为v 0 = mv/(m + M ) = 2(m·s -1),这也是它们振动的初速度.子弹和木块压缩弹簧的过程机械能守恒,可得(m + M ) v 02/2 = kA 2/2,所以振幅为A v =-2(m). (2)振动的圆频率为ω=s -1).取木块静止的位置为原点、向右的方向为位移x 的正方向,振动方程可设为x = A cos(ωt + φ).当t = 0时,x = 0,可得φ = ±π/2;由于速度为正,所以取负的初位相,因此振动方程为x = 5×10-2cos(40t - π/2)(m).4.4 如图所示,在倔强系数为k的弹簧下,挂一质量为M 的托盘.质量为m 的物体由距盘底高h 处自由下落与盘发生完全非弹性碰撞,而使其作简谐振动,设两物体碰后瞬时为t = 0时刻,求振动方程.[解答]物体落下后、碰撞前的速度为v =物体与托盘做完全非弹簧碰撞后,根据动量守恒定律可得它们的共同速度为0m v v m M ==+这也是它们振动的初速度. 设振动方程为x = A cos(ωt + φ),其中圆频率为ω=物体没有落下之前,托盘平衡时弹簧伸长为x 1,则x 1 = Mg/k .物体与托盘碰撞之后,在新的平衡位置,弹簧伸长为x 2,则x 2 = (M + m )g/k .取新的平衡位置为原点,取向下的方向为正,则它们振动的初位移为x 0 = x 1 - x 2 = -mg/k . 因此振幅为图4.3图4.4A===初位相为arctanvxϕω-==4.5重量为P的物体用两根弹簧竖直悬挂,如图所示,各弹簧的倔强系数标明在图上.试求在图示两种情况下,系统沿竖直方向振动的固有频率.[解答](1)可以证明:当两根弹簧串联时,总倔强系数为k=k1k2/(k1+ k2),因此固有频率为2πων===.(2)因为当两根弹簧并联时,总倔强系数等于两个弹簧的倔强系数之和,因此固有频率为2πων===4.6 一匀质细圆环质量为m,半径为R,绕通过环上一点而与环平面垂直的水平光滑轴在铅垂面内作小幅度摆动,求摆动的周期.[解答]方法一:用转动定理.通过质心垂直环面有一个轴,环绕此轴的转动惯量为I c = mR2.根据平行轴定理,环绕过O点的平行轴的转动惯量为I = I c + mR2 = 2mR2.当环偏离平衡位置时,重力的力矩为M = -mgR sinθ,方向与角度θ增加的方向相反.根据转动定理得Iβ = M,即22dsin0dI mgRtθθ+=,由于环做小幅度摆动,所以sinθ≈θ,可得微分方程22ddmgRt Iθθ+=.摆动的圆频率为ω=周期为2πTω=22==方法二:用机械能守恒定律.取环的质心在最底点为重力势能零点,当环心转过角度θ时,重力势能为E p = mg(R - R cosθ),绕O点的转动动能为212kE I=ω,总机械能为21(cos)2E I mg R R=+-ωθ.环在转动时机械能守恒,即E为常量,将上式对时间求导,利用ω= dθ/d t,β=dω/d t,得0 = Iωβ + mgR(sinθ)ω,由于ω ≠ 0,当θ很小有sinθ≈θ,可得振动的微分方程22ddmgRt Iθθ+=,从而可求角频率和周期.[注意]角速度和圆频率使用同一字母(b)图4.5ω,不要将两者混淆.4.7 横截面均匀的光滑的U 型管中有适量液体如图所示,液体的总长度为L ,求液面上下微小起伏的自由振动的频率。
大学物理振动习题答案

Sg
第4页/共32页
2. 解:
x 0.10cos(20 t )
4
①
振幅: A 0.10(m)
频率: 1 10(Hz) T 2
角频率: 20
周期: 初相:
T 2 0.1(s)
4
第5页/共32页
② 根据:
x Acos(t ) v A sin(t )
a A2 cos(t )
解:①
A 0.1m, 2 ,
3
T 2 1 s, 4
8 4Hz
vm A 0.8 (m/s) 2.51(m/s)
am 2 A 63.2(m/s2 ) 第10页/共32页
②: Fm mam 0.63N
E
1 2
mvm2
3.16 102 J
EP
Ek
1E 2
1.58 102 J
因此证明物体作简谐振动。
第15页/共32页
若两弹簧最初都处于原长状态 当质点 m 产生位移 x 时
f k2 x k1 x (k1 k2 )x kx 同样的结果! 总之,并联弹簧
k k1 k2
第16页/共32页
②振动的角频率和振幅分别为:
k k1 k2 2 10(rad/s)
将 t 代2s 入,得:
x 2 (m) 20
v 2 (m/s)
a 20 2 2(m/s2 )
第6页/共32页
例题 :
普通物理学教案
一个轻质弹簧竖直悬挂,下端挂一质量 为m 的物体。今将物体向下拉一段距离后再 放开,证明物体将作简谐振动。
解:平衡位置 kl mg
l mg k
以平衡位置o为原点建坐标
m
m
A
x02
机械振动基础作业(有答案-全版)
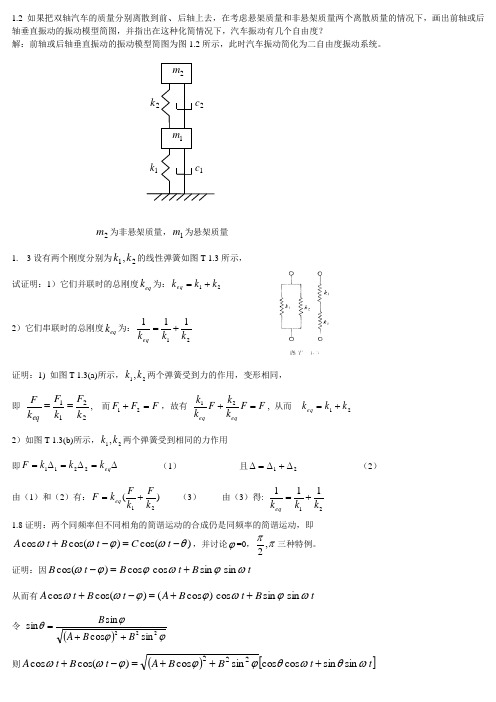
1.2 如果把双轴汽车的质量分别离散到前、后轴上去,在考虑悬架质量和非悬架质量两个离散质量的情况下,画出前轴或后轴垂直振动的振动模型简图,并指出在这种化简情况下,汽车振动有几个自由度?解:前轴或后轴垂直振动的振动模型简图为图1.2所示,此时汽车振动简化为二自由度振动系统。
2m 为非悬架质量,1m 为悬架质量1. 3设有两个刚度分别为21,k k 的线性弹簧如图T-1.3所示, 试证明:1)它们并联时的总刚度eq k 为:21k k k eq +=2)它们串联时的总刚度eq k 为:21111k k k eq +=证明:1) 如图T-1.3(a)所示,21,k k 两个弹簧受到力的作用,变形相同, 即2211k F k F k F eq ==, 而F F F =+21,故有 F F k kF k k eq eq =+21, 从而 21k k k eq +=2)如图T-1.3(b)所示,21,k k 两个弹簧受到相同的力作用 即∆=∆=∆=eq k k k F 2211 (1)且21∆+∆=∆ (2)由(1)和(2)有:)(21k Fk F k F eq += (3) 由(3)得:21111k k k eq += 1.8证明:两个同频率但不同相角的简谐运动的合成仍是同频率的简谐运动,即)cos()cos(cos θωϕωω-=-+t C t B t A ,并讨论ϕ=0,ππ,2三种特例。
证明:因t B t B t B ωϕωϕϕωsin sin cos cos )cos(+=-从而有t B t B A t B t A ωϕωϕϕωωsin sin cos )cos ()cos(cos ++=-+令 ()ϕϕϕθ222sin cos sin sin B B A B ++=则()[]t t B B A t B t A ωθωθϕϕϕωωsin sin cos cos sin cos )cos(cos 222+++=-+=())cos(sin cos 222θωϕϕ-++t B B A令C=()ϕϕ222sin cos B B A ++,则有 )cos()cos(cos θωϕωω-=-+t C t B t A当ϕ=0时,C=A+B ;当ϕ=2π时,22B A C +=,22BA arcsin +=B θ ;当ϕ=π时,B A -=C ,0=θ1.13汽车悬架减振器机械式常规性能试验台,其结构形式之一如图T-1.13所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小质量m的绝对速度为: 2 & & & & & & && va = x12 + y12 = 4R2θ 2 + x2 + 4x2θ 2 + 4Rxθ cos3θ −8Rxθ 2 sin3θ
3
第5章分析力学基础
习题
第5章分析力学基础
习题
r sinα = Rcos3θ 方法2: ΔOBA中 2 2 2 有:r = R + x − 2 Rx cos(90° − 3θ ) = R 2 + x 2 − 2 Rx sin 3θ 小质量m的绝对速度
ω
2 2
2+ 2 k = J 2
ω
2 R
k = 3J
3k ω′ = 10 J
2 R
ω
2 1
2 1
k ≈ 4J
⎫ 2 θ2 )⎪ ⎪ 2 ⎬ 2 θ2 )⎪ ⎪ 2 ⎭
方法1:广义坐标、频率和主振型都与题3-3相同。待定常数由 初始角速度为零,初始转角为[0, 0.01]T,代入下式得到。( ω 不等于 ω1和 ω2)
1 ⎤ ⎧ A1 cos (ω1t − ϕ1 ) ⎫ ⎧θ1 ⎫ ⎡ 1 ⎨ ⎬=⎢ ⎬ ⎥⎨ ⎩θ 2 ⎭ ⎣ 2 − 2 ⎦ ⎩ A2 cos (ω 2t − ϕ 2 )⎭
+
kT sin ω t ⎧ ⎫ 1 ⎬ 2 2 2 ⎨ 2 J ω − 4 Jk ω + k ⎩ ( 2 k − 2 J ω )T sin ω t ⎭
习题
⎧1 ⎪ (θ1 + θ ⎪2 1 ⎤ ⎧ y1 ⎫ −1 ⎧ 1 ⎫ 1 ⎤ 1 ⎡ 1 ⎡1 ⎨ ⎬ = [u ] ⎨ ⎬ = ⎨ [u ] = [u] = ⎢ ⎢ ⎥ ⎩θ 2 ⎭ ⎪ 1 2 J ⎣ 2 − 2 ⎦ ⎩ y2 ⎭ 2 − 2⎥ ⎣ ⎦ ⎪ 2 (θ1 − ⎩
ω 12 =
2− 2 k J 2
第6章 非线性振动 6-1 分析单摆在ϕ=π时奇点的性质(系统 无阻尼)。
& ϕ& + g sin ϕ = 0 l
习题
6-2 求出下列方程的奇点,并指出其类型
&& + x + x 3 = 0 x 奇点: & x = 0, x = 0
奇点为中心。
6-3 用直接展开法求出方程的一阶渐近解
& && + x − ε x 2 = 0 x(0) = A, x(0) = 0 x 2 2 2 ⎛A ⎞ A A 2 x = A cos t + ε ⎜ ⎟ ⎜ 2 − 3 cos t − 6 cos 2t ⎟ + 0(ε ) ⎝ ⎠
mL && mgL kA θ + cθ& + ( k − 2 )θ = cos ω t a a2 a k Aa cos (ω t − Φ ) θ = ( ka 2 − mgL ) (1 − ω 2 ) 2 + ( 2ζω ) 2 ω 2ζ ω a 2k g ω = Φ = arctan − ωn = ωn 1−ω 2 mL2 L
第5章分析力学基础 习题 5-1 质量为m、半径为R的均质圆柱体,沿 半径为3R的内圆柱表面作无滑滚动。圆柱 体的端面有一质量可忽略的光滑导轨,一 小质量m用两个刚度为k的弹簧与导轨两端 连接,起始时质量m处于静平衡位置时圆柱 体的中心,如右图所示。试利用Lagrange 方程导出系统作微振动的微分方程。 方法1: 广义坐标为x和θ。小质量m的位置 为A,在O1-x1y1坐标系中的坐标为: x1 = 2 R sin θ + x cos 2θ y1 = 2 R cosθ + x sin 2θ 小质量m的速度在x1轴和y1轴上的分量分别 & & & 为: Rθ cosθ + x cos2θ − 2xθ sin 2θ y = −2Rθ sinθ + x sin 2θ + 2xθ cos2θ & & & & x =2 &
边界条 件: 设: y
4-3 设悬臂梁的右端带有一体积较大的质量,试写出梁 作横向振动时,右端点的边界条件。
∂2 ⎡ ∂ 2 y (x, t) ⎤ ∂ 2 y (x, t) 0< x < L ⎢EI (x) ⎥ = m (x) 2 2 ∂x ⎢ ∂x ∂ t2 ⎥ ⎣ ⎦ 1 d 2 F (t ) = −ω 2 设 y ( x, t ) = Y ( x ) F ( t ) 有 d t2 F (t ) 2 ⎡ 2 d Y ( x ) ⎤ :2 : d −
P ⎞ Jω2 ⎟ = 2 Θ ( x) x = L ⎟ GI P ⎠ x=L
βi
GI P J
Θi ( x) = a
第4章 连续系统
习题
4-2 设梁的左端由横向弹簧和扭转弹簧支承,试写出梁 作横向振动时,左端点的边界条件。
∂ 2 y ( x, t ) ∂2 ⎡ ∂ 2 y ( x, t ) ⎤ − ⎢ EI ( x ) ⎥ = m ( x) 2 2 ∂ t2 ∂x ⎢ ∂x ⎥ ⎣ ⎦
1 1
ωi = ( i π) 2
EI mL
4
, Yi (x) =
2 iπ sin x ( i = 1, 2, L) mL L
y ( x, t ) = ∑
i =1
∞
(−1)i +1 2 L3 F (2i − 1) π sin x sin ωt 4 4 4 2 (2i − 1) π EI − mL ω L
习题
设:广义坐标θ 为直角杆的转角,图示位置为零,逆时 针为正。
ζ =
a 2c 2 L m( ka 2 − mgL)
−k3 ⎤ k 3 + k 4⎥ ⎦
⎧ x 1 ⎫ ⎧0⎫ ⎨ ⎬=⎨ ⎬ ⎩ x 2 ⎭ ⎩0⎭
2-4 弹簧-质量系统,从t = 0时,突 加一个F0 力,以后该力保持不变。试 用Duhamel积分求系统的响应。 2-5 一仪器要与发动机的频率从 1600 rpm 到2200 rpm 范围 实现振动隔离,若要隔离85%,仪器安装在隔振装置上时, 隔振装置的静变形应为多少?(2.68 mm)
势能零点在系统静平衡时O点位置,Lagrange函数L:
L= 1 1 1 m ( 2 R θ& ) 2 + ( mR 2 )( 2θ& ) 2 2 2 2 1 & & + m ( 4 R 2θ& 2 + x 2 + 4 x 2θ& 2 + 4 R x θ& cos 3θ − 8 Rx θ& 2 sin 3θ ) 2 1 − 2 mgR (1 − cos θ ) − 2 mgR (1 − cos θ ) + mgx sin 2θ + ( 2 kx 2 ) 2
1
第3章 多自由度线性系统的振动 3-3 图示扭转振动系统中, k1 = k2 = k,J1 = 2 J2 = 2 J。 求系统的固有频率 和主振型;正则化振型矩阵和主坐标; 用三种方法估算系统的基频,并与精确 解作比较。
广义坐标如图。
习题
第3章 多自由度线性系统的振动 3-4 图示扭振系统中,时间 为零时,两盘的初始角速度为 零,端部的小盘初始转角为 0.01弧度。求系统的全响应。
则有:
d 2Y ( x) kt dY ( x) = EI dx dx 2
d 3Y ( x) k = − Y ( x) dx 3 EI
M的惯性力与惯性力矩大小为: ∂2 ⎡ ∂y ( x, t ) ⎤ ∂ 3 y ( x, t ) PI = M 2 ⎢ y ( x, t ) + l MI = J ∂t ⎣ ∂x ⎥ x = L ⎦ ∂t 2 ∂x x = L 边界条件(A点): ∂ 2 y ( x, t ) ∂ 3 y ( x, t ) Q = EI = − M I − PIl = PI M = EI ∂x 2 x = L ∂x 3 x = L 3 dY ( x ) d Y ( x) 或 = − Mω 2Y ( L) − Mlω 2 EI dx x = L dx 3 x = L :
设:广义坐标x 为质量 m1 和 m2的位移,向下为正,弹 簧-质量m2和 m1系统静平衡时为零。
x (t ) =
m2
2gh
( m1 + m 2 ) k
sin
m2 g k k t− cos t m1 + m 2 k m1 + m 2
第2章 单自由度线性系统的振动 2-3 试导出图示系统的振动微分方程,并求 系统的稳态响应、半功率带宽。
3-2 如图所示,绳索上有两个质量 m1 和 m2 ( m1 = 2 m2 ), 各段绳索中的张力均为T ,用柔度法建立系统作微振动的微 分方程。
设:广义坐标x1 和 x2分别为质量 m1 和 m2的位移,向下为正,系统 静平衡时为零。
x ⎡ 2 0⎤ ⎧ && 1 ⎫ T ⎡ 2 − 1⎤ ⎧ x 1 ⎫ ⎧0⎫ ⎢0 1⎥ ⎨ && ⎬ + m L ⎢ − 1 2 ⎥ ⎨ x ⎬ = ⎨0⎬ ⎣ ⎦ ⎩x 2 ⎭ ⎣ ⎦ ⎩ 2⎭ ⎩ ⎭ 2
试用状态空间法求系统的响应。
4-1 设图示轴系由长度为L、单位长度 转动惯量为J、扭转刚度为GIP的均匀杆 和转动惯量为J2的刚性薄圆盘组成,轴 系一端固定。求解轴系作扭转振动时系 统的特征值问题。
⎡− 3 − 3.25⎤ [N ] = ⎢ 0 ⎥ ⎣1 ⎦
d 2 Θ ( x) dx
2
+ β 2 Θ ( x) = 0
4
EI d 2Y ( x) dx 2 = ( J + Ml 2 )ω 2
