轴心受压构件
合集下载
(轴心)受压构件正截面承载力计算

(2)破坏特征 1)螺旋筋或焊接环筋在约束 核心混凝土的横向变形时产生 拉应力,当它达到抗拉屈服强 度时,就不再能有效地约束混 凝土的横向变形,构件破坏。 2)螺旋筋或焊接环筋外的混 凝土保护层在螺旋筋或焊接环 筋受到较大拉应力时就开裂, 故在计算时不考虑此部分混凝 土。
螺旋箍筋柱破坏情况
2.适用条件和强度提高原理 12(短柱) ; (1)适用条件:①l0 / d ②尺寸受到限制。 注意:螺旋箍筋柱不如普遍箍筋柱经济,一般不宜采用。 根据图7-8 所示螺旋箍筋柱截面 受力图式,由平衡条件可得到
150mm或15倍箍筋直径(取较大者)范围,则应设置复合箍 筋。
a)、b)S内设3根纵向受力钢筋
c)S内设2根纵向 受力钢筋
复合箍筋的布置
7.2 螺旋箍筋轴心受压构件
1.受力分析及破坏特征 (1)受力分析 螺旋箍筋或焊接圆环箍筋能约束混凝土在轴向压力作用 下所产生的侧向变形,对混凝土产生间接的被动侧向压力,
d cor As 01
S
As 01
As 0 S d cor
将式(2)代入式(1),则可得到
2
2 f s As 01 2 f s As 0 S 2 f s As 0 f s As 0 f s As 0 2 2 d cor S d cor S d cor 2 Acor d cor d cor 2 4
态、承载力计算;
2.配有纵向钢筋和螺旋箍筋的轴心受压构件的破坏形 态、承载力计算; 3.稳定系数的概念及其影响因素; 4.核心混凝土强度分析及强度计算;
5.普通箍筋柱、螺旋箍筋柱的配筋特点和构造要求。
7.1 普通箍筋轴心受压构件
1.钢筋混凝土轴心受压柱的分类
普通箍筋柱:配有纵筋 和箍筋的柱 (图7-1a)。 螺旋箍筋柱:配有纵筋 和螺旋筋或焊接环筋的 柱,(图7-1b)。 其中:纵筋帮助受压、承 担弯矩、防止脆性破坏。 螺旋筋提高构件的强 度和延性。
第七章 轴心受压构件

二、破坏形态
2、结论(2)
长柱破坏——失稳破坏 破坏特征:凹侧砼先被压碎, 砼表面有纵向裂缝;凸侧则 由受压突然转为受拉,出现 横向裂缝;破坏前,横向挠 度增加很快,破坏来得比较 突然,导致失稳破坏。
§7-2 普通箍筋柱-课题1概述
二、破坏形态
2、结论(3) 长柱的承载力<短柱的承载力
(相同材料、截面和配筋)
§7-1 概 述
真正意义上的轴 心受压构件是不 存在的。 如果偏心距很小, 在工程设计中容 许忽略不计时, 按轴心受压构件 计算。
说明:sv——箍筋间距;d——箍筋直径; dcor——混凝土核心直径
§7-1 概 述
二、钢筋混凝土轴心受压构件的类型 1、划分标准:根据箍筋的功能和配置方式划分。 2、类型:
短柱:通过 试验,随着 压力逐渐增 加,柱体随 之缩短,说 明混凝土全 截面和纵向 钢筋均发生 压缩变形。
二、破坏形态
§7-2 普通箍筋柱-课题1概述
二、破坏形态
短柱体的受力分析
Ps
As′
钢筋屈服
混凝土压碎
h
Pc
b
A
Ps
o
l
第一阶段:加载至钢筋屈服
混凝土压碎
第二阶段:钢筋屈服至混凝土压碎
钢筋凸出
§7-2 普通箍筋柱-课题1概述
一、构造要求
1.混凝土 一般多采用C20~C30级混凝土。
2.截面尺寸 截面尺寸不宜小于250mm,长细比不大于30。
3.纵向钢筋:多采用HRB335、HRB400等热轧钢筋。 直径:12~32mm ,根数≥4 ,纵筋之间净距
50mm≤Sn≤350mm, 净保护层:≥30mm。
§7-2 普通箍筋柱-课题1概述
2、结论(2)
长柱破坏——失稳破坏 破坏特征:凹侧砼先被压碎, 砼表面有纵向裂缝;凸侧则 由受压突然转为受拉,出现 横向裂缝;破坏前,横向挠 度增加很快,破坏来得比较 突然,导致失稳破坏。
§7-2 普通箍筋柱-课题1概述
二、破坏形态
2、结论(3) 长柱的承载力<短柱的承载力
(相同材料、截面和配筋)
§7-1 概 述
真正意义上的轴 心受压构件是不 存在的。 如果偏心距很小, 在工程设计中容 许忽略不计时, 按轴心受压构件 计算。
说明:sv——箍筋间距;d——箍筋直径; dcor——混凝土核心直径
§7-1 概 述
二、钢筋混凝土轴心受压构件的类型 1、划分标准:根据箍筋的功能和配置方式划分。 2、类型:
短柱:通过 试验,随着 压力逐渐增 加,柱体随 之缩短,说 明混凝土全 截面和纵向 钢筋均发生 压缩变形。
二、破坏形态
§7-2 普通箍筋柱-课题1概述
二、破坏形态
短柱体的受力分析
Ps
As′
钢筋屈服
混凝土压碎
h
Pc
b
A
Ps
o
l
第一阶段:加载至钢筋屈服
混凝土压碎
第二阶段:钢筋屈服至混凝土压碎
钢筋凸出
§7-2 普通箍筋柱-课题1概述
一、构造要求
1.混凝土 一般多采用C20~C30级混凝土。
2.截面尺寸 截面尺寸不宜小于250mm,长细比不大于30。
3.纵向钢筋:多采用HRB335、HRB400等热轧钢筋。 直径:12~32mm ,根数≥4 ,纵筋之间净距
50mm≤Sn≤350mm, 净保护层:≥30mm。
§7-2 普通箍筋柱-课题1概述
轴心受力构件
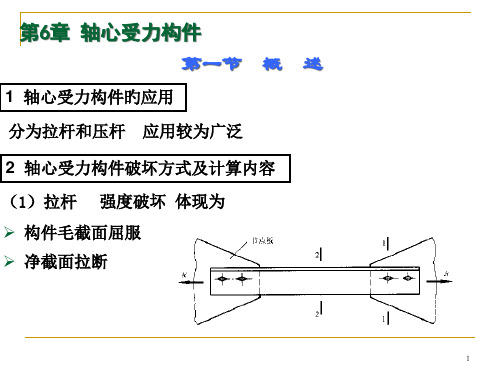
失稳现象发生在构成构件旳板件
18
第6章 轴心受力构件 第三节 轴心受压构件旳受力性能
2 承载力极限状态旳计算内容 (1)截面强度破坏
(2)构件整体失稳(屈曲)
(3)板件局部失稳(屈曲) 限制受压板件旳宽厚比
19
第6章 轴心受力构件 第三节 轴心受压构件旳受力性能
3 稳定问题旳某些概念 (1)应力刚化效应 拉力提升构件旳弯曲刚度 压力降低 (2)只要构件旳截面中存在受压区域,就可能存在稳定问题 (3)强度问题是应力问题,针正确是构件最单薄旳截面,加大截面 积即可提升构件旳强度,计算以净截面为准 (4)稳定问题是刚度(变形)问题,针正确是构件整体,减小变形 (提升刚度)旳措施都能够提升构件旳稳定性,计算以毛截面为准
➢ 根据截面残余应力旳峰值大小和分布,弯曲屈曲旳方向,将截面 分为a、b、c三类,相应地得到a、b、c三条柱子曲线
44
第6章 轴心受力构件 第七节 规范中实腹式轴压构件弯曲屈曲时整体稳定计算
➢ a类截面临界应力最高,残余应力对临界应力起有利作用或影响 很小,只涉及两种截面: ✓ 绕强(x)轴屈曲时旳热轧工字钢和热轧中翼缘、窄翼缘H型钢 ✓ 热轧无缝钢管
(1)发生弯扭屈曲旳条件 ✓ 截面形式:单轴对称截面 ✓ 失稳方向:绕对称轴失稳。绕非对称轴失稳必然是弯曲失稳 ✓ 原因:形心和剪心不重叠,弯曲时截面绕剪心转动
51
第6章 轴心受力构件 第八节 实腹式轴压构件弯扭屈曲时整体稳定计算
(2)单角钢截面、双角钢组合截面弯扭屈曲旳规范计算措施 ➢ 用换算长细比 (考虑扭转效应)替代弯曲屈曲时旳长细比 查得稳定系数 ,再按下列公式验算杆件旳稳定
42
第6章 轴心受力构件 第七节 规范中实腹式轴压构件弯曲屈曲时整体稳定计算
18
第6章 轴心受力构件 第三节 轴心受压构件旳受力性能
2 承载力极限状态旳计算内容 (1)截面强度破坏
(2)构件整体失稳(屈曲)
(3)板件局部失稳(屈曲) 限制受压板件旳宽厚比
19
第6章 轴心受力构件 第三节 轴心受压构件旳受力性能
3 稳定问题旳某些概念 (1)应力刚化效应 拉力提升构件旳弯曲刚度 压力降低 (2)只要构件旳截面中存在受压区域,就可能存在稳定问题 (3)强度问题是应力问题,针正确是构件最单薄旳截面,加大截面 积即可提升构件旳强度,计算以净截面为准 (4)稳定问题是刚度(变形)问题,针正确是构件整体,减小变形 (提升刚度)旳措施都能够提升构件旳稳定性,计算以毛截面为准
➢ 根据截面残余应力旳峰值大小和分布,弯曲屈曲旳方向,将截面 分为a、b、c三类,相应地得到a、b、c三条柱子曲线
44
第6章 轴心受力构件 第七节 规范中实腹式轴压构件弯曲屈曲时整体稳定计算
➢ a类截面临界应力最高,残余应力对临界应力起有利作用或影响 很小,只涉及两种截面: ✓ 绕强(x)轴屈曲时旳热轧工字钢和热轧中翼缘、窄翼缘H型钢 ✓ 热轧无缝钢管
(1)发生弯扭屈曲旳条件 ✓ 截面形式:单轴对称截面 ✓ 失稳方向:绕对称轴失稳。绕非对称轴失稳必然是弯曲失稳 ✓ 原因:形心和剪心不重叠,弯曲时截面绕剪心转动
51
第6章 轴心受力构件 第八节 实腹式轴压构件弯扭屈曲时整体稳定计算
(2)单角钢截面、双角钢组合截面弯扭屈曲旳规范计算措施 ➢ 用换算长细比 (考虑扭转效应)替代弯曲屈曲时旳长细比 查得稳定系数 ,再按下列公式验算杆件旳稳定
42
第6章 轴心受力构件 第七节 规范中实腹式轴压构件弯曲屈曲时整体稳定计算
第4章轴心受力构件1211

轴 心 受 力 构 件
强度 (承载能力极限状态) 轴心受拉构件 刚度 (正常使用极限状态) 强度 轴心受压构件 稳定 刚度 (正常使用极限状态)
(承载能力极限状态)
设计轴心受拉构件时,应根据结构用途、构件受 力大小和材料供应情况选用合理的截面形式,并对所 选截面进行强度和刚度计算。 设计轴心受压构件时,除使截面满足强度和刚度 要求外尚应满足构件整体稳定和局部稳定要求。实际
结构构件,稳定计算比强度计算更为重要。强度问题与 稳定问题虽然均属第一极限状态问题,但两者之间概念 不同。强度问题关注在结构构件截面上产生的最大内力 或最大应力是否达到该截面的承载力或材料的强度,强 度问题是应力问题;而稳定问题是要找出作用与结构内 部抵抗力之间的不稳定平衡状态,即变形开始急剧增长
的状态,属于变形问题。
N f An ,1 其中:An ,1 b n1 d 0 t ;
f 钢材强度设计值 ; d 0 螺栓孔直径; b 主板宽度;t 主板厚度。
拼接板的危险截面为2-2截面。
考虑孔前传力50%得: 2-2截面的内力为:
2
t1 t b
N
b1
N
0.5n2 N 0.5 N 1 n 2 n2 计算截面上的螺栓数; n 连接一侧的螺栓总数。 N f 其中:An , 2 b1 n2 d 0 t 1 ; An , 2
上,只有长细比很小及有孔洞削弱的轴心受压构件,
才可能发生强度破坏。一般情况下,由整体稳定控制 其承载力。 轴心受压构件丧失整体稳定常常是突发性的,容 易造成严重后果,应予以特别重视。
§4-2 轴心受力构件的强度和刚度
一、强度计算(承载能力极限状态)
钢筋混凝土轴心受压构件计算

3.螺旋筋不能提升强度过多,不然会造成混凝土保护层剥
落,即 N 螺 1 .5 N 普 1 .3( 5 fcA d fs ' A d s ')
§6.2 配有纵向钢筋和螺旋箍筋旳轴心受压构件
五、构造要求 1、螺旋箍筋柱旳纵向钢筋应沿圆周均匀分布,其截面积应
不不不小于箍筋圈内关键截面积旳0.5%。常用旳配筋率在
二、破坏形态
1.影响原因: (1)徐变:
●使钢筋应力忽然增大,砼应力减小(应力重分布) ●忽然卸载砼会产生拉应力。 (2)长细比:(l0/b) 2.一般箍筋柱旳破坏特征 (1)短柱破坏——材料破坏。
破坏特征:纵向裂缝、纵筋鼓起、砼崩裂。
承载能力
PSfcAfs'dAs' |
(2)长柱破坏——失稳破坏 破坏特征:凹侧砼先被压碎,
式中 为作用于关键混fc凝c土f旳c径k向2压应力值。
2
§6.2 配有纵向钢筋和螺旋箍筋旳轴心受压构件 三、承载力计算
螺旋箍筋柱正截面承载力旳计算式并应满足
0 N d ≤ N u 0 . 9 f c A c d o k s r A d s 0 f f s 'A d s '
★★螺旋筋仅能间接地提升强度,对柱旳稳定性问题 毫无帮助,所以长柱和中长柱应按着通箍筋柱计算, 不考虑螺旋筋作用。
As' f1s'd(0r0.9Nd fcdA)
2)截面复核 已知截面尺寸,计算长度l0,全部纵向钢筋旳截面面 积,混凝土轴心抗压强度和钢筋抗压强度设计值,轴向力 组合设计值,求截面承载力。
§6.1 配有纵向钢筋和一般箍筋旳轴心受压构件
五、构造要求 1.混凝土 一般多采用C25~C40级混凝土。 2.截面尺寸 ① lo /②b30 ③2尺5寸2模c5m 数化: 25,30,
第5章轴心受压构

φ--稳定系数,按附录表4-3、4-4、4-5、5-6采用。
5.6实腹式轴心受压构件的局部稳定
5.6.1概述 组成构件的板件出现鼓曲 称为板件失稳,即局部失 稳。 板件的局部失稳并不一定 导致整个构件丧失承载能 力,但由于失稳板件退出 工作,将使能承受力的截 面(称为有效截面)面积 减少,同时还可能使原本 对称的截面变得不对称, 促使构件整体破坏。
N
2 cr , x 1 cr , y
I e, x Ix
2 (k b) t (h / 2) k 2 2 b t ( h / 2)
2
N N
I e, y Iy
2 cr , y
t (k b) 3 / 12 k3 t b 3 / 12
焊接工字钢残余应力分布
由于k小于1,对这样的残余应力分布,其对y轴稳定承 载力的影响比对x轴要大的多。
对板件的稳定目前有两种处理方法,一是不容许出现 板件失稳,二是板件可以失稳,利用其屈曲后强度, 但要求板件受到的轴力小于板件发挥屈曲后强度的极 限承载力。考虑屈曲后强度的轴压杆设计目前用于薄 壁型钢轴压杆。 5.6.2实腹轴心压杆中板件的临界应力 1、板件的分类 根据板件两边支承情况将其分为加劲板件、部分加劲 板件和非加劲板件三种。 加劲板件为两纵边均与其他板件相连接的板件; 部分加劲板件即为一纵边与其他板件相连,另一纵边 为卷边加劲的板件,在薄壁型钢中普片存在;
5.4.1格构式轴心受压构件绕实轴(y-y轴)的整体稳定
格构式轴心受压构件绕实轴(y-y轴)的整体稳定承载力 计算和实腹式轴心受压构件完全相同。 5.4.2格构式轴心受压构件绕虚轴(x-x轴)的整体稳定 构式轴心受压构件绕虚轴发生弯曲失稳时,所产生的 剪力由缀材承担,缀材抵抗剪变形的能力小,剪力产 生的剪切变形大,对整体稳定承载力的不利影响必须 予以考虑。 2 EI 1 即 N
轴心受压构件

其中,4、5、6均属于初始缺陷。
以上各因素都不是孤立的。
第13页/共77页
5.3.3 轴心压杆的弯曲失稳、扭转失稳、弯扭失稳
(1) 具有初始缺陷的任意非对称开口薄壁轴心 压杆弯扭失稳弹性微分方程,对任一截面取:
Z ( ) N
Y(v)
X(u)
M x 0, M y 0, M z 0
第14页/共77页
第9页/共77页
a)理想轴心压杆欧拉临界应力
l/2
p 2 EI
Ncr NE l 2
NE — 欧拉(Euler)临界力
欧拉临界应力
scr
sE
NE A
pl
2EI 2A
pl
2E(
2
I A
)2
p2E
l2
i
2
(pl/2iE)2pl2E2
l/2
图 有初弯曲的 轴心压杆
λ——杆件长细比,λ=l/i;
i ——截面对应于屈曲的回转半径, i = I/A。
3.不对称截面均的弯扭失稳
当压杆的截面无对称轴时,微分方程即为公式。 这三个微分方程是互相联立的,因此,杆件失稳时必 定是弯扭变形状态,属于弯扭失稳。
EI EI
x y
(v(4) (u ( 4 )
v0(4) ) u0(4) )
Nv'' Nu
Nx0 '' '' Ny0
''
0 0
EI (
(4)
弯曲屈曲:双轴对称截面,单轴对称截面绕非对称轴; 扭转屈曲:十字形截面; 弯扭屈曲:单轴对称截面(槽钢,等边角钢)。
第6页/共77页
第7页/共77页
5.2 轴心受压构件的强度 以净截面的平均应力强度为准则,即
以上各因素都不是孤立的。
第13页/共77页
5.3.3 轴心压杆的弯曲失稳、扭转失稳、弯扭失稳
(1) 具有初始缺陷的任意非对称开口薄壁轴心 压杆弯扭失稳弹性微分方程,对任一截面取:
Z ( ) N
Y(v)
X(u)
M x 0, M y 0, M z 0
第14页/共77页
第9页/共77页
a)理想轴心压杆欧拉临界应力
l/2
p 2 EI
Ncr NE l 2
NE — 欧拉(Euler)临界力
欧拉临界应力
scr
sE
NE A
pl
2EI 2A
pl
2E(
2
I A
)2
p2E
l2
i
2
(pl/2iE)2pl2E2
l/2
图 有初弯曲的 轴心压杆
λ——杆件长细比,λ=l/i;
i ——截面对应于屈曲的回转半径, i = I/A。
3.不对称截面均的弯扭失稳
当压杆的截面无对称轴时,微分方程即为公式。 这三个微分方程是互相联立的,因此,杆件失稳时必 定是弯扭变形状态,属于弯扭失稳。
EI EI
x y
(v(4) (u ( 4 )
v0(4) ) u0(4) )
Nv'' Nu
Nx0 '' '' Ny0
''
0 0
EI (
(4)
弯曲屈曲:双轴对称截面,单轴对称截面绕非对称轴; 扭转屈曲:十字形截面; 弯扭屈曲:单轴对称截面(槽钢,等边角钢)。
第6页/共77页
第7页/共77页
5.2 轴心受压构件的强度 以净截面的平均应力强度为准则,即
轴心受压构件的弯曲屈曲_图文

讨论
(1)v0是P的非线性函数,当P =0时, v0=0,但一开始加载杆件即发生 弯曲;
(2)v0在加载初期增长较慢,后随P的加大而增长加快,当 P→PE时,v→,以欧拉临界力为渐进线;
(3)偏心较大时临界力明显低于欧拉临界力;若偏心很小,
则v0在P→PE前都很小。 与初弯曲的影响无本质区别。
轴压杆的分岔屈曲荷载,在数学上是一个求特征值的问题 。 与k值对应的y(x)为特征函数或特征向量,即构件处于中性 平衡时的弹性曲线方程。
= 0为特征方程,因Pcr由 = 0求得,故又称为屈曲方程
§2 轴心受压构件的弯曲屈曲
一端铰接、一端固定的轴心压杆 边界条件:
线性齐次方程组:
几何边 界
扭转失稳:扭转变形迅速增大而丧失承载力。 十字形截面
弯扭失稳:单轴对称构件绕对称轴失稳时,截面形心与剪心 不重合,发生弯曲的同时伴有扭转。 单轴对称截面,无对称轴截面
弯曲屈曲是确定轴心受压构件 稳定承载力的主要依据。
§2 轴心受压构件的弯曲屈曲
荷载位移曲线
1-小挠度理论 (弹性) 2-大挠度理论 (弹性) 3-有初弯曲时(弹性) 4-有初偏心时(弹性) 3’-有初弯曲时(弹塑性
§2 轴心受压构件的弯曲屈曲 §2.3 轴心受压构件的大挠度弹性理论
1)大挠度方程
构件弯曲曲率与变 形的关系:
两端铰接轴压杆大 挠度方程为:
§2 轴心受压构件的弯曲屈曲
2)讨论
(1)当P<PE时,小、大挠度理论都表明构件处于直线稳 定平衡状态;
(2)当P≥PE时,小挠度理论只能指出构件处于随遇平衡 状态,只能给出分岔点和屈曲变形形状,不能给出确 定的挠度值;而大挠度理论不仅能说明构件屈曲后仍 处于稳定平衡状态,而且可以得到不同时刻的荷载与 挠度关系;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五、板件相互约束对稳定承载力影响
板件相互影响
考虑板件相互影响的单板修正——采用板组约束系数
xcr
k
2E 12(1
2)
t2 b2
xcr
k
2E 12(1
2)
t2 b2
直接采用计入板相互影响的稳定系数 k k(约束系数)
p.99 表5-6
第4节 轴心压杆中板件的局部稳定 §5.6.3, P101-103
EIω ''' GIt ' Nx0v' Ny0u'( Nr02 R ) ' 0
整体失稳变形平衡方程基本假定
——弹性
II
——小变形:包括弯曲变形u, v和扭转变形
——以变形后位置建立平衡方程(几何非线性) I
弯曲平衡 (以第1式为例)
剪力中心沿 y 轴挠度,由平衡产生 M x1 N v
形心位置发生扭转,再产生
N : 0 NE*x
w v vm
N
N
N Ex
NE* x
v
第3节 实腹式轴心压杆的整体稳定
七、非弹性失稳
E
2E 2
fy
?
N
* E
2E*A 2
fy
理论演变
a) Engesser 切线模量假定
b) Engesser 双模量假定
c) Shanley 切线模量理论
Et
E Et
Et
σ
弹塑性状况
e
Et
当 0.215 =(A- A2 4 2 ) / 2 2 A=2 +3 + 2
其中系数
1、
、
2
3
按截面分类确定,数值由p.85
表5-3得到
——查表法 截面分类→计算长细比→查附录4 (p.340-344) 直接得到
第3节 实腹式轴心压杆的整体稳定 §5.5, P91
九、工程计算方法
工程计算原理
一、薄板受压时的失稳变形和平衡方程
理想轴心受压薄板
——板件平直,厚度相等 ——板件宽度b和厚度t之比大于10
N
x
——轴压均匀分布,作用板的中面
受压薄板的弯曲失稳
t
y
xb
a
t
w
受压薄板弹性失稳的平衡方程
4w D( x4
2
4w x2y4
4w y4 )
Nx
2w x2
0
——单位板宽抗弯刚度
D Et3
12(1 2)
临界力 N Ey 2 EI y / L2oy
两联立方程的求解:p. 87-88
1 ( NEx
1 NEθ
)
NEω
(1
x02 ) r02
NE2ω NEx NEθ
1
NEω
能否从上式推导无对称轴截面的理想压杆稳定临界承载力?
能否推导出 弯扭失稳时的换算长细比 (p.88 公式5-37)?
第3节 实腹式轴心压杆的整体稳定 §5.3.4, P83-85
结构系统中的“压杆”
第1节 概述
第1节 概述 参阅§4.1.1, P66, §5.1, P77-78
截面形式和破坏类型
受压构件的截面 (参见 p.66)
双轴对称截面、单轴对称截面、无对称轴截面/实腹式、格构式
构件破坏类型
——截面强度破坏:截面有较大削弱处或非常粗短的构件 ——构件整体失稳:弯曲失稳、扭转失稳、弯扭失稳 p.97 ——构件中板件的局部失稳
mb (
a
n2a)2 mb
m、n的几何意义(波数图形)
n
=1时临界力有最小值
Nxcr n1
2D
b2
( mb a
a )2 mb
k
2D
b2
p.98图5-16
Nxcr
2D
4 b2
2E
4
12(1
2)
t3 b2
临界应力
xcr
Nxcr t
4
2E
b2 /
12(1 2) t2
宽厚比
第4节 轴心压杆中板件的局部稳定 §5.6.2, P98-99
截面上任一点都存在杆轴方向应力
dAa '
dAa(s) ' a(s) ' a(s)2 dA Nr02 '
r02
Ix
Iy A
x
2 0
y
2 0
d
dz
' a(s)2 rdA ' R
a
dA
ad
a d
y
dAa ' x
a(s)
dAa(s) ' ad / dz a '
双轴对称截面的平衡方程
zN
Nv'
x0
EIω ''' GIt ' Nx0v' Ny0u'( Nr02 R ) ' 0 v
约束扭转与翘曲
y
Nv' y
x
对剪心求矩 略去高阶量
轴线弯曲引起的扭转分量 N v ' x0 , N u ' y0 N
M z1 Nv'x0
本坐标系中
x0 为负值
纵向应力(残余应力)对扭转平衡的影响
(5-10)
NE ( 2EIω / L2o GIt R) / r02 2EA/ 2 (5-11)
式中计算长度与边界约束条件有关, 长细比(5-21)~(5.23)
双轴对称截面3个微分方程独立,得到3个解,对应3种失稳模态
杆端弯曲约束和扭转约束的自由、铰支、固接
约束对应的计算长度系数 p.81
轴心受压构件
Axially Compressive Member
第一节 概述 第二节 截面强度 第三节 实腹式轴心压杆的整体稳定 第四节 轴心压杆中板件的局部稳定 第五节 格构式轴心压杆的整体稳定和肢杆稳定 第六节 轴心受压构件的刚度 第七节 轴心受压构件的设计计算
结构系统中的“压杆”
第1节 概述
失稳临界应力 E NE / A 2E / 2
讨论:3种临界力中何者控制压杆的承载力?
第3节 实腹式轴心压杆的整体稳定 §5.3.3, P82, §5.3.5, P87-88
四、单轴对称截面理想压杆的临界力
基本方程之一解耦(设 x 轴为对称轴)
EIxv'' Nv Nx0 0
EIxv'' Nv Nx0 0
y
x
x
— 横向力过该点不产生扭矩
y — 无外扭矩构件只受弯、剪
x0 y
x0
— 该点为截面扭转的不动点
y0
形心 剪力中心
z
L
第3节 实腹式轴心压杆的整体稳定 参阅§3.1, P48-51, §5.3, P78-81
二、理想压杆弹性失稳的平衡方程
EIxv'' Nv Nx0 0 EIyu'' Nu Ny0 0
二、理想压杆弹性失稳的平衡方程
EIxv'' Nv Nx0 0 EIyu'' Nu Ny0 0
EIω ''' GIt ' Nx0v' Ny0u'( Nr02 R ) ' 0
教材(5.5)
截面坐标、剪力中心概念 (弯曲中心,扭转中心) 由形心轴规定的剪力中心坐标
x
x0
x y0
x
y
y
N N ult cr A ( cr / f y ) Af y Af y N Af d
注意点: ——整体稳定计算采用毛截面 ? ——采用设计规范的轴压构件稳定系数 计算步骤 ——确定轴力设计值 ——计算构件长细比(针对不同轴线!) ——确定轴压构件稳定系数 ——稳定校核
第4节 轴心压杆中板件的局部稳定 §5.1.3, P78, §5.6.2, P97
EI x v IV Nv '' 0
EI x
Ebh 3 12
——单位板宽上的轴压力 N x
平衡方程的物理意义及与杆件的比较
第4节 轴心压杆中板件的局部稳定 §5.6.2, P97-98
二、四边简单支承板的稳定临界力
四边简单支承板 (边界上挠度、弯矩为零) 四边简单支承板的临界力
Nxcr
2D
b2
N
第3节 实腹式轴心压杆的整体稳定 §5.3.3, P80-83
三、双轴对称截面理想压杆的临界力
失稳临界力
EI xv'' Nv Nx0 0
EI xv'' Nv 0
N Ex
2 EI x
L2ox
2 EAI
x
/
A
2
EAi
2 x
L2ox
L2ox
2 EA 2x
(5-9)
同理
NEy 2EIy / L2oy 2EA/ 2y
四边简支: k=4.0;
三边简支,与压力平行一边自由:k =0.425+(b / a)2
三边简支,与压力平行一边有卷边支承: k=1.35
结论:约束越强,稳定系数就越大,临界应力越高
第4节 轴心压杆中板件的局部稳定 §5.6.2, P98-100
四、宽厚比、弹性与非弹性稳定
稳定临界应力与宽厚比
xcr
六、板件失稳后性能
板件失稳后性能特点
——屈曲后强度
屈曲后强度物理原因和
cr
数学分析
fy
cr1
屈曲后强度会否高于屈服点?
屈曲后强度与屈服点的比较
cr2 cr3
板件 压杆
v w
w
第4节 轴心压杆中板件的局部稳定 §5.6.3, P103-104
板件相互影响
考虑板件相互影响的单板修正——采用板组约束系数
xcr
k
2E 12(1
2)
t2 b2
xcr
k
2E 12(1
2)
t2 b2
直接采用计入板相互影响的稳定系数 k k(约束系数)
p.99 表5-6
第4节 轴心压杆中板件的局部稳定 §5.6.3, P101-103
EIω ''' GIt ' Nx0v' Ny0u'( Nr02 R ) ' 0
整体失稳变形平衡方程基本假定
——弹性
II
——小变形:包括弯曲变形u, v和扭转变形
——以变形后位置建立平衡方程(几何非线性) I
弯曲平衡 (以第1式为例)
剪力中心沿 y 轴挠度,由平衡产生 M x1 N v
形心位置发生扭转,再产生
N : 0 NE*x
w v vm
N
N
N Ex
NE* x
v
第3节 实腹式轴心压杆的整体稳定
七、非弹性失稳
E
2E 2
fy
?
N
* E
2E*A 2
fy
理论演变
a) Engesser 切线模量假定
b) Engesser 双模量假定
c) Shanley 切线模量理论
Et
E Et
Et
σ
弹塑性状况
e
Et
当 0.215 =(A- A2 4 2 ) / 2 2 A=2 +3 + 2
其中系数
1、
、
2
3
按截面分类确定,数值由p.85
表5-3得到
——查表法 截面分类→计算长细比→查附录4 (p.340-344) 直接得到
第3节 实腹式轴心压杆的整体稳定 §5.5, P91
九、工程计算方法
工程计算原理
一、薄板受压时的失稳变形和平衡方程
理想轴心受压薄板
——板件平直,厚度相等 ——板件宽度b和厚度t之比大于10
N
x
——轴压均匀分布,作用板的中面
受压薄板的弯曲失稳
t
y
xb
a
t
w
受压薄板弹性失稳的平衡方程
4w D( x4
2
4w x2y4
4w y4 )
Nx
2w x2
0
——单位板宽抗弯刚度
D Et3
12(1 2)
临界力 N Ey 2 EI y / L2oy
两联立方程的求解:p. 87-88
1 ( NEx
1 NEθ
)
NEω
(1
x02 ) r02
NE2ω NEx NEθ
1
NEω
能否从上式推导无对称轴截面的理想压杆稳定临界承载力?
能否推导出 弯扭失稳时的换算长细比 (p.88 公式5-37)?
第3节 实腹式轴心压杆的整体稳定 §5.3.4, P83-85
结构系统中的“压杆”
第1节 概述
第1节 概述 参阅§4.1.1, P66, §5.1, P77-78
截面形式和破坏类型
受压构件的截面 (参见 p.66)
双轴对称截面、单轴对称截面、无对称轴截面/实腹式、格构式
构件破坏类型
——截面强度破坏:截面有较大削弱处或非常粗短的构件 ——构件整体失稳:弯曲失稳、扭转失稳、弯扭失稳 p.97 ——构件中板件的局部失稳
mb (
a
n2a)2 mb
m、n的几何意义(波数图形)
n
=1时临界力有最小值
Nxcr n1
2D
b2
( mb a
a )2 mb
k
2D
b2
p.98图5-16
Nxcr
2D
4 b2
2E
4
12(1
2)
t3 b2
临界应力
xcr
Nxcr t
4
2E
b2 /
12(1 2) t2
宽厚比
第4节 轴心压杆中板件的局部稳定 §5.6.2, P98-99
截面上任一点都存在杆轴方向应力
dAa '
dAa(s) ' a(s) ' a(s)2 dA Nr02 '
r02
Ix
Iy A
x
2 0
y
2 0
d
dz
' a(s)2 rdA ' R
a
dA
ad
a d
y
dAa ' x
a(s)
dAa(s) ' ad / dz a '
双轴对称截面的平衡方程
zN
Nv'
x0
EIω ''' GIt ' Nx0v' Ny0u'( Nr02 R ) ' 0 v
约束扭转与翘曲
y
Nv' y
x
对剪心求矩 略去高阶量
轴线弯曲引起的扭转分量 N v ' x0 , N u ' y0 N
M z1 Nv'x0
本坐标系中
x0 为负值
纵向应力(残余应力)对扭转平衡的影响
(5-10)
NE ( 2EIω / L2o GIt R) / r02 2EA/ 2 (5-11)
式中计算长度与边界约束条件有关, 长细比(5-21)~(5.23)
双轴对称截面3个微分方程独立,得到3个解,对应3种失稳模态
杆端弯曲约束和扭转约束的自由、铰支、固接
约束对应的计算长度系数 p.81
轴心受压构件
Axially Compressive Member
第一节 概述 第二节 截面强度 第三节 实腹式轴心压杆的整体稳定 第四节 轴心压杆中板件的局部稳定 第五节 格构式轴心压杆的整体稳定和肢杆稳定 第六节 轴心受压构件的刚度 第七节 轴心受压构件的设计计算
结构系统中的“压杆”
第1节 概述
失稳临界应力 E NE / A 2E / 2
讨论:3种临界力中何者控制压杆的承载力?
第3节 实腹式轴心压杆的整体稳定 §5.3.3, P82, §5.3.5, P87-88
四、单轴对称截面理想压杆的临界力
基本方程之一解耦(设 x 轴为对称轴)
EIxv'' Nv Nx0 0
EIxv'' Nv Nx0 0
y
x
x
— 横向力过该点不产生扭矩
y — 无外扭矩构件只受弯、剪
x0 y
x0
— 该点为截面扭转的不动点
y0
形心 剪力中心
z
L
第3节 实腹式轴心压杆的整体稳定 参阅§3.1, P48-51, §5.3, P78-81
二、理想压杆弹性失稳的平衡方程
EIxv'' Nv Nx0 0 EIyu'' Nu Ny0 0
二、理想压杆弹性失稳的平衡方程
EIxv'' Nv Nx0 0 EIyu'' Nu Ny0 0
EIω ''' GIt ' Nx0v' Ny0u'( Nr02 R ) ' 0
教材(5.5)
截面坐标、剪力中心概念 (弯曲中心,扭转中心) 由形心轴规定的剪力中心坐标
x
x0
x y0
x
y
y
N N ult cr A ( cr / f y ) Af y Af y N Af d
注意点: ——整体稳定计算采用毛截面 ? ——采用设计规范的轴压构件稳定系数 计算步骤 ——确定轴力设计值 ——计算构件长细比(针对不同轴线!) ——确定轴压构件稳定系数 ——稳定校核
第4节 轴心压杆中板件的局部稳定 §5.1.3, P78, §5.6.2, P97
EI x v IV Nv '' 0
EI x
Ebh 3 12
——单位板宽上的轴压力 N x
平衡方程的物理意义及与杆件的比较
第4节 轴心压杆中板件的局部稳定 §5.6.2, P97-98
二、四边简单支承板的稳定临界力
四边简单支承板 (边界上挠度、弯矩为零) 四边简单支承板的临界力
Nxcr
2D
b2
N
第3节 实腹式轴心压杆的整体稳定 §5.3.3, P80-83
三、双轴对称截面理想压杆的临界力
失稳临界力
EI xv'' Nv Nx0 0
EI xv'' Nv 0
N Ex
2 EI x
L2ox
2 EAI
x
/
A
2
EAi
2 x
L2ox
L2ox
2 EA 2x
(5-9)
同理
NEy 2EIy / L2oy 2EA/ 2y
四边简支: k=4.0;
三边简支,与压力平行一边自由:k =0.425+(b / a)2
三边简支,与压力平行一边有卷边支承: k=1.35
结论:约束越强,稳定系数就越大,临界应力越高
第4节 轴心压杆中板件的局部稳定 §5.6.2, P98-100
四、宽厚比、弹性与非弹性稳定
稳定临界应力与宽厚比
xcr
六、板件失稳后性能
板件失稳后性能特点
——屈曲后强度
屈曲后强度物理原因和
cr
数学分析
fy
cr1
屈曲后强度会否高于屈服点?
屈曲后强度与屈服点的比较
cr2 cr3
板件 压杆
v w
w
第4节 轴心压杆中板件的局部稳定 §5.6.3, P103-104
